1.числовой ряд.Сходимость ряда.св-ва сходящихся рядов
Числовой ряд
— бесконечная последовательность чисел соединенная знаком +. Ряды задаются 1.перечислением первых несколькихъ членов 1+1/2+1/3+1/4+….
2. формулой общего члена. 
Если  частичных сумм при n->∞ существует и равен конечному чисоу то соответствует ряд называется сходящийся и его сумма равна Si в противном случае ряд расходящийся частичных сумм при n->∞ существует и равен конечному чисоу то соответствует ряд называется сходящийся и его сумма равна Si в противном случае ряд расходящийся
Если основание >1 ряд сходится
Если основание < 1 ряд сходится
Если основание=1 ряд расходится
Если основание равно =-1 то предел не существует и ряд расходится
Св-ва сходящихся рядов
1.Если ряд а1+а2+а3+…an сходится то и ряд сходится
2. Пусть ряд  и и 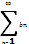 и их сумма =S1. S2 тогда ряд и их сумма =S1. S2 тогда ряд 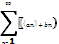 также сходится также сходится
3. если ряд сходится аn тогда и сходится и ряд полученный из данного путем отбрас конечного числа члена
4. для того чтобы ряд сходился необходимо и достаточно чтобы при n->∞ остаток ряда стремится к 0
|
2. Ряды с положительными членами. признаки сходимости.
1. необходимый признгак сходимости если ряд сходиттся то предел его общего члена при n->∞=0Если предел общего члена не равен 0 то рад расход2. признак сравненияЕсли сходится ряд 2 то сходится и 1. Если расход 1 то и расход 2.Ряды используемые для сравнения1. Геометрич2. Гармонический3. Обобщенный гармонический ряд3.предельный признак сравненияЕсли  и и 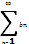 ряды с положит членами и сущ конечный предел членов стрем к ∞ то ряды сходятся или расход одновременно4. Признак даламбераПусть ряд с положите членами при n->∞ сущ ряды с положит членами и сущ конечный предел членов стрем к ∞ то ряды сходятся или расход одновременно4. Признак даламбераПусть ряд с положите членами при n->∞ сущ  =LТогдаЕсли L<1 расходЕсли L>1 расходЕсли L=1 не раб5.Радикальный признак КошиЕсли ряд сходится с положит членами суш предел =LТогдаЕсли L<1 расходЕсли L>1 расходЕсли L=1 не раб5.Радикальный признак КошиЕсли ряд сходится с положит членами суш предел  Если L<1 сходЕсли L>1 расходЕсли L=1 не работает6. Интегральный признакДля сходимости ряда необходимо и достаточно чтобы сходился не собств интеграл Если L<1 сходЕсли L>1 расходЕсли L=1 не работает6. Интегральный признакДля сходимости ряда необходимо и достаточно чтобы сходился не собств интеграл |
3.Знакочередующие ряды. Признак Лейбница. абсолютная и условная сходимость
Знакопеременные ряды назыв если его члены произвол знака
Условие необходимости: если ряд составленный из абсолютных величин членов данного ряда сходится и данный ряд тоже.
Ряд назвается абсолютно сходящ если сходится как сам ряд так и ряд сставленный из абсолют величины его члена
Ряд называется условно сходящ если сам ряд составл из абсолютных величин.(расход)
Теорема пр-ка Лейбница: если член знакочередующ ряда убывает по абсолют величине и предел абсолют величины его общего члена =0 то ряд сходится а его сумма не превосходит его первого члена
|
4.Степенные ряды. Область сходимости
Функциональный ряд называют степенным если он имеет вид 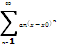
Функциональные ряды если его члены явл функ
U1(x)+u2(x)+….+un(x)
Все знач X при которых функц ряда сходится является областью сходимости функц ряда
S(x) на области сход сумма ряда явл функ среди функ назыв степенные ряды
Алгоритм нах обл сход
1. Найдем радиус сход по одной из формул
2. Строим интерв сход (-R;R)
3. Ислед поведен ряда на границах интервала
4. Запис область
|
5. Ряд маклорена
Для того чтобы ряд маклорена сходлился в функции f(x) необходимо и достаточно чтобы n->∞ и остаток ряда стремился к 0.
Если f(x) разложима ряд маклрена то это разложение единственно
|
6. Периодические поцессы. Тригонометрический ряд Фурье
Периодические функции f(x)с периодом T если x+t€ области определения и F(x+t)=f(x)
Простейшим гармоническим процессом является простое гармон колебание которое описыв функц y=A(sin(wt-γ0)
А-амплитуда, w-чистота колеб, t- время, γ- номинальная фаза
Тригонометрич рядом наз функционал ряд вида 
|
7.Разложение ряда фурье функций 2п
теорема Дирихле.
1. F(x) кусочно непрерывный т.е непрерывна илиимеет конечное число точек первого рода
2. f(x) кусочно-монотонно т.е на всем отрезке или на том отрезке можно разюбить на конечное число отрезков. Тогда соответств функции F(x) ряд фурье сход на этом отрезке
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов
|
8. Разложение ряда фурье четных и нечетных функций.
Пусть функция y
= f
(x
) задана на сегменте [п,-п]и удовлетворяет условиям Дирихле.
Пусть функция f(x)–чётная и удовлетворяет теореме Дирихле. Тогда функции f(x)*cosnx–нечётные, а f(x)*sinnx – при любых n
=1,2,... Поэтому 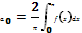
,
Пусть функция f(x)нечётная и удовлетворяет теореме Дирихле. Тогда функции f(x)*cosnx– нечётные, а f(x)*sinnx– четные при любых n
=1,2,... Поэтому a0=0, an=0

|
9.Применение рядов в приближенных вычислениях
 (1) и требуется хотя бы приближенно, вычислить значение f(x) для каких – либо значений x, то естественно пользоваться приближенными формулами f(x)≈Sn(x) (2) где Sn(x)-частичная сумма ряда. При вычислении по формулам (2) может быть достигнута любая точность в силу равенства (1), но возможно, что потребуется брать Sn(x) с очень большим номером n. Не всегда легко оценивать прогрешнсть формулы (2) это посто сделать для знакочередующегося ряда, но если ряд не знакочередкющийся, а например положительный то приходится подтыскивать мажорантный ряд для него n-го остатка данного ряда и подыскивать еготак чтобы его сумма легко вычислялась (1) и требуется хотя бы приближенно, вычислить значение f(x) для каких – либо значений x, то естественно пользоваться приближенными формулами f(x)≈Sn(x) (2) где Sn(x)-частичная сумма ряда. При вычислении по формулам (2) может быть достигнута любая точность в силу равенства (1), но возможно, что потребуется брать Sn(x) с очень большим номером n. Не всегда легко оценивать прогрешнсть формулы (2) это посто сделать для знакочередующегося ряда, но если ряд не знакочередкющийся, а например положительный то приходится подтыскивать мажорантный ряд для него n-го остатка данного ряда и подыскивать еготак чтобы его сумма легко вычислялась
Если ряд (1) настолько медленно сходится, что не пригоден для приближенного вычисления его суммы f(x) то обычно стараются построить другой более быстро сходящийся ряд с той же суммой f(x)
|
10. Основные принципы комбинаторики. Примеры. Основные формулы комбинаторики
Принцип суммы
Если некоторый объект А
может быть выбран из совокупности объектов N1 способами, а объект В
N2 способами, то выбор либо объекта А либо объекта В может быть осуществлен N1+N2 способами.
Принцип произведения
Если объект А может быть выбран из совокупности объектов N1 способами, а после такого выбора объект В может быть выбран N2 способами, то пара объесков А и В могут быть выбраны N1*N2 способами.
Или это +
И это *
Формулы соединения кобинаторики
1) Число комбинаций содержащих m элементов взятых из данных m и отличающихся друг от друга и составом элементов или их порядком назыв размещения из n по m обознач 
2) комбинации содержат n-эементов которое отличается друг от друга порядком след элементов назыв перестновками по n
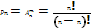 или Pn=n! или Pn=n!
3)число комбинаций содержит m элементов взятых из данных n которые отличаются элементами называется сочетаниями из n по m
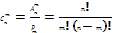
|
11. Предмет теории вероятности. Событие
Событие-возможный рез-тат некоторого испытания
1.Достоверные-событие которое всегда наступает в рез-те испытания
2.Невозможное,событие которое никогда не наступает в рез-те испытания
3.Случайное,событие которое может наступить,а может и не наступить в рез-те испытания.
Теория вероятности наз-ся изучением закономерности массовых,многократных,однородных, случайных событий.
1.Совместные события-если появление одного из них не исключает появление остальных.
2.Несовместное событ.-появление одного не исключают появления другого в одном испытании
Несколько событий образуют полную группу событий если в результате опыта обязательно появится хотя бы одно из них.
Если два несовместных события образуют полную группу они называются противоположными
События называется равновозможными если появление ни одного из них не является объективно более возможным чем другие.
События называются неравновозможными если появление хотя бы одного из них является более возможным чем другие.
Случаями называются несовместные равновозможные и образующие полную группу события.
|
12.классификация случайных событий
События называется несовместными
в данном опыте если появление одного из них исключает появление другого.
События называется совместными
если появление одного из них не исключает появление остальных.
Несколько событий образуют полную группу
событий если в результате опыта обязательно появится хотя бы одно из них.
Если два несовместных события образуют полную группу они называются противоположными
События называется равновозможными
если появление ни одного из них не является объективно более возможным чем другие.
События называются неравновозможными
если появление хотя бы одного из них является более возможным чем другие.
Случаями
называются несовместные равновозможные и образующие полную группу события.
|
13.Операции над событиями
1.Суммой событий а и b наз-ся новое событие состоящее хотя бы одного из этих событий если (∞)то этот ряд_____ сумма будет сущ.если ряд сходится.
2.Произведение 2-х событий состоящее в наступление обоих событий
|
14.Отнсительная частота события. Св-ва
Отностельной частотой событий называется отношение чисел испытаний закончившихся появлением событий к числу всех испытаний W(A)=m/nm-сколько раз появлялось событие
n- сколько раз поводилось событие
Св-ва частоты
1) относительная частота невозможного события=0
2)относит частота достоверного события =1
3)Отнсит частота случайного события =1
|
15.Статистическое определение вероятности. Св-ва
Вероятность события называется число вокруг которого группируются относительные частоты событий
Св-ва
Достоверного 1
Невозможн 0
Случайного 1
|
16.Класическое определение вероятностию. Св-ва
Вероятностью события А наз-ют отношение числа исходов благоприятствующих появлению события
А- число исходов
Св-ва
Достоверного 1
Невозможн 0
Случайного 1
|
17.Геометрическое определение вероятности. Св-ва
Отношение меры благоприятно появляется событие к общей мере отношений.
Св-ва
Достоверного= 1
Невозможн= 0
Случайного =1
|
18. Теорема сложения вероятностей несовместных событий
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А1+А2)=Р(А1)+Р(А2)
Следствие
1. вероятность суммы nне совм событ = сумме их вероятности P(A1+A2+…..An)= Р(А1)+Р(А2)+…Р(An)
2.сумма вероятности n несовм событий образующ полную группу=1
3. Р(А)+Р( =1 =1
|
19. Теорема умножения вероятностей
.
Событие А называется зависимым от события В если его вероятность меняется в зависимости от того произошло событие В или нет.
Для независимых событий условная и безусловная вероятность совпадают.
Вероятность появления двух зависимых событий равна произведению вероятностей одного из них на вероятность другого вычисленную при условии, что первое событие имело место. Р(А*В)=Р(А)*Р(В/А)=Р(В)*Р(В/А)
Вероятность произведения нескольких событий равна произведению вероятностей этих событий причем вероятность каждого следующего события вычисляется при условии, что все предыдущие имели место. Р(А1
;А2
…Аn
)=Р(А1
)*Р(А2
/А1
)*… *Р(Аn
/А1
,А2
…Аn-1
)
|
20. Теорема сложения вероятностей совместных событий
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Р(А)+Р(В)=Р(А)+Р(В)-Р(А*В)
Вероятность появления хотя бы одного события
Вероятность появления события А заключающееся в наступлении хотя бы одного из независимых совокупностей событий .А1
,А2
…Аn
равна разности между единицей и произведением вероятности противоположных событий А1
,А2
…Аn
Р(А)=1-q1
*q2
*…*qn
|
21. Формула полной вероятности
Пусть событие А может появиться вместе с одним из образующих полную группу попарнонесовместных событий Н1
,Н2
…Нn
называемых гипотезами, тогда вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на вероятность события А при этой гипотезе

|
22. Формулф Байеса
Пусть имеется полная группа попарнонесовместных гипотез Н1
,Н2
…Нn
с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло
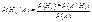
|
23.Формула Бернули.
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А
.
Формула Бернулли
— формула в теории вероятности, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний.
Следствия: 1)Вероятность того что события испытаний наступит не менее к1 и не более к2
2) Вероятность того что в n-опытах событие А появится хотя бы 1 раз Pn=1-
|
24 Формула Пуассона.
При большом числе испытаний n
и малой вероятности р
формулой Бернулли пользоваться неудобно, например, 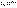 вычислить трудно. В этом случае для вычисления вероятности того, что в n
испытаниях (n
– велико) событие произойдет k
раз, используют формулу Пуассона
: вычислить трудно. В этом случае для вычисления вероятности того, что в n
испытаниях (n
– велико) событие произойдет k
раз, используют формулу Пуассона
:
|
25 Локальная теорема Лапласа.
Если число испытаний велико (n→∞) , вероятность появления события постоянна и отлична от нуля и от единицы, то вероятность того, что в n испытаниях событие наступить ровно k раз равна (чем больше n, тем точнее) следующему выражению.  ; ;

|
26 Интегральная теорема Лапласа
Теорема. Если вероятность Pпоявления события Aв каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k1,k2) того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна определенному интегралу  . В ней приведены значения функции Ф(х)(которую называют функцией Лапласа) Св-ва: Если x>5, то Ф(х)=0.5. . В ней приведены значения функции Ф(х)(которую называют функцией Лапласа) Св-ва: Если x>5, то Ф(х)=0.5.
Для х<0 пользуются той же таблицей и свойством нечетности функции Лапласа, то есть Ф(-х)=-Ф(х)
Следствие: Если имеет место повторения испытания исполнения то число К в наступлении события А отличается от произведения np неболее чем на величину E по абсолютной величине. Вычисляется по формуле  частотность(m/n) событие А заключена (£<β) частотность(m/n) событие А заключена (£<β)
Вероятность отклонения относительной частоты от постоянной вероятности вычисляется по формуле 
|
27. наивероятнейшее число появления события
Np-q≤k0≤np+p (n
- число испытаний; p
- вероятность появления события при одном испытании)
1.Границы дробные k0 ед. целое число из полученного промежутка
2. Если границы целые то принимает два возможных значения имеющих одинаковую вероятность
|
28. Простейший поток событий
Поток событий- последовательность событий которые наступают в случайные моменты времени. Св-ва 1. Св-во стационарности-вероятность к появлению К собыбий в любой промежуток времени.
2. Св-во отсутствий последствий-взаимная независимость того или инного числа событий в непеременающие моменты времени
3 Св-во Ординарности-когда бесконечно малый промежуток времени появляется не более одного события
Поток событий который обладает св-ми стациорнарности отсутствия последственности всеми тремя назыв простейшими или пуасоновскими.
Среднее число событий которое появляется в ед времени назыв интенсивности потока. 
|
29 Случайная величина. закон распределения вероятностей
С.В в результате принимает то или инное значение но заранее до пыта не известна
Закон распределения С.В. называют соответствие между возможными знгачениями случайной величины к соответствующими вероятности этих возможных значений
Способы задания : 1. Табличный 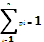 2. Графический 3. Аналитический 2. Графический 3. Аналитический
Дискретными
называются случайные величины принимающие отдельные изолированные друг от друга значения, которые можно переоценить.
Ряд и многоугольник распределения.
Простейшей формой закона распределения дискретной величины является ряд распределения.
Графической интерпретацией ряда распределения является многоугольник распределения.
Непрерывными
величины возможные значение которых непрерывно заполняют некоторый диапазон.
|
30 Функция распределения С.В и ее св-ва
Для непрерывных случайных величин применяют такую форму закона распределения, как функция распределения.
Функция распределения случайной величины Х, называется функцией аргумента х, что случайная величина Х принимает любое значение меньшее х (Х<х)
F(х)=Р(Х<х)
F(х) - иногда называют интегральной функцией распределения или интегральным законом распределения.
Св-ва:
1. F
(x
)определена на всей числовой прямой R
;
2.F
(x
)не убывает, т.е. если x
1
≤x
2
, то F
(x
1
)≤ F
(x
2
);
3.
 и и
4.F
(x
) непрерывна справа, т.е. 
|
31 Плотность распределения С.В и ее св-ва
Плотность распределения вероятности непрерывной случайной величины Х называется функция f(х) равная первой производной от функции распределения F(х)
График плотности распределения называется кривой распределения.
Основные свойства плотности функции распределения:
1. 1. f(х)>0
2. 2. 
3. 3
4. 4.
|
32 Математическое ожидание С.В. Свойства
Математическим ожиданием случайной величины х (M
[
x
]
)называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности появления тех или иных значений.
Для дискретной случайной величины

Для непрерывной
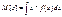
Математическое ожидание случайной величины всегда больше наименьшего значения и меньше наибольшего.
Св-ва
М(с)=С
М(сх)=СМ(х)
М(х±У)=М(х)±М(У)
М(х*У)=М(х)*М(У)
М(х±С)=М(х)±С
|
33Дисперсия С.В. Свойства. Средне квадратическое отклонение
Дисперсия
Дисперсия (
D
[
x
])
характеризует рассеивание или разряженность случайной величины около ее математического ожидания.
Для дискретных

Для непрерывных


Дисперсия случайной величины всегда величина положительная
Размерность дисперсии равна квадрату разности случайной величины
Св-во: 1.D(c)=0
2.D(cx)= D(x) D(x)
3.D(x)=M(
Среднеквадратическое (стандартное) отклонение .

|
34 Мода и медиана С.В
Мода СВ наиболее вероятное значение СВ
Медиана- называет такое ее значение относит которого равновероятного получения большего или меньшего значения С.В
|
35 Закон распределения Дискретных С.В
Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения
дискретной
случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения
.
Графическое представление этой таблицы называется многоугольником распределения.
При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Распределение дискретных случайных величин для некуоторых ряд распределения задается формулой бернули

|
36 Закон распределения непрерывных С.В
С В имеет равномерное распределение если на отрезке АВ плдотность распределения= постояннаа вне этого отрезка =0

|
37 Нормальный Закон распределения. Правило трех сигм
Нормальный закон распределения также называется законом Гаусса
.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Правило трёх сигм
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм
.
вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм
.
На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
|
38 Предмет мат.статистики. Основные понятия. Выборочный метод
Иследуемые признаки все объекты обладающие этим признаком образуют генеральную совокупность
N-объем генеральных совокупностей
n- объем выборки, кол-во которых были подвергнуты иследованию
Выборка представляет совокупность n чисел
Наблюдаемое значение признака наз-ся вариантален обозначим через Хi из чисел найти самое большое и самое маленьеое xmin и xmax
Совокупность чисел (x1,x2….xn), полученных в результате n-кратного повторения опыта по измерению генеральной совокупности x, называется реализацией случайной выборки
или просто выборкой объёма
n.
В основе большинства результатов математической статистики лежит выборочный метод
, состоящий в том, что свойства генеральной совокупности x устанавливаются путём изучения тех же свойств на случайной выборке.
1.Если n не велико то выборку просто ронжируют в порядке возвр и убывания
2.Если среди вариантов имеются повтряющие то строят дискрет вариационный ряд
Выборка бывает повторная и бесповторная
Повторной называют при которрой отборный эффект возвращается в генеральную совокупность
Бесповторной называю при которой отборный объект в ген совокуп не возвращается.
На практике используют чаще всего бесповторную
|
39 Представление выборки
Графическое представление выборки
1) Полигон- для представления дискретного вариационного ряда представляет собой ломанную с вершинами Wi=ni/n
2) Гистограмма фигура поставленная из прямоугольн основаниями которые являются интервлы длиной n и высоты
Для гистограмма частот m/n
Относит частот Wi’/n
Империческая функция распределения выступает кумулятивная кривая для дискретного ряда представляет собой ломанную соед точками XiNi
|
40 Числовые храктеристики выборки
Выборочная средняя
- это, очевидно, средняя арифметическая из случайных величин (Х1
; Х2
; …Хn
):
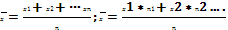

Выборочная дисперсияDв
1)Dв=
2)Dв=
3)
Мода
- наз-е вариант у котор имеется наибольшая частота

Х0- начало модального интервала имеюх мах частоту
h- длина интервала
ni- частота модал интервала
ni-1
-частота предмодальная
ni+1
– частота постмодальная
Медиана-
значение серединного элемента вариационного ряда
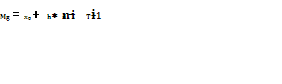
X0-начало медианного интервала.
hi – частота
Ti-1
-сумма частот интервалов предеств к медианному
|
41 Оценка параметров распределения. Требования к оценке. Точечные оценки
Оценка является случайной величиной .
Требования к оценке.
1. должна быть не смещенной не должно быть ни всторону повышения ни в сторону занижения M(θ*
)=θ
2. возможные значения (θ*
) должны быть менее рассеяны в округление среднего значения D(θ*
)->θ
3. состоятельность оценки означает что при увеличении объема выборки значение оценки должно-> к истинному знач оценивающий параметра при увеличении объема выборки.
1) выборочная средняя является не смещенной состоят эффектив оценки для генеральн среднего т.е для матожидания ислед признака
2) Выборочная дисперсия является смещенной и состоят оценкой для генеральной писперсии
Несмещенной и состоят дисперсией является исправленнная выборочная Д  оценки описывающие одним числом назыв точечнымиS-точност оценки оценки описывающие одним числом назыв точечнымиS-точност оценки
Чем меньше сигра тем лучше оценки.
|
42. Оценка параметров распределения. Требования к оценке. Интервальные оценки
Оценка является случайной величиной .
Требования к оценке.
1. должна быть не смещенной не должно быть ни всторону повышения ни в сторону занижения M(θ*
)=θ
2. возможные значения (θ*
) должны быть менее рассеяны в округление среднего значения D(θ*
)->θ
3. состоятельность оценки означает что при увеличении объема выборки значение оценки должно-> к истинному знач оценивающий параметра при увеличении объема выборки.
Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок
Чем γ ближе к ед то интервал больше
Доверительный интервал для оценки нормальн распределения σ 
Доверительный интервал для оценки нормальн распределения при не известном σ 
Доверительный интервал для оценки среднеквадратического отклонения нормального распределеного признака 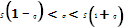
|
43 понятие о стат. Гипотезе и ее проверка
Для проверки гипотез используют специально подобранные С.В называемые критериями точное распределение которых известно. Все множество значений критерия делится на критическую область и обюласть принятия гопотез.
Критерии бывают правосторонние, левосторонние и двухсторонние
|
44. критерии согласия Пирсона
Критерий Пирсона, или критерий χ2
(Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.
|