Курсовая работа: Основы расчёта оболочек
|
Название: Основы расчёта оболочек Раздел: Промышленность, производство Тип: курсовая работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Омский государственный технический университет Кафедра “Авиа- и ракетостроение” Специальность 160801 - “Ракетостроение” Курсовая работа по дисциплине “Строительная механика летательных аппаратов” Основы расчёта оболочек Омск 2005 Содержание 1. Расчет цилиндрической оболочки, подкрепленной шпангоутами 2. Исследование напряжённо-деформированного состояния полусферической оболочки, заполненной жидкостью 3. Исследование напряжённо-деформированного состояния сферической оболочки, заполненной жидкостью 4. Расчёт сферического топливного бака с опорой по экватору 5. Расчёт бака на прочность Список литературы 1. РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, ПОДКРЕПЛЕННОЙ ШПАНГОУТАМИ Условие задачи.
Рассмотрим цилиндрическую оболочку постоянной толщины Цель расчета.
Определить минимальное расстояние между шпангоутами
Рис.1. Расчетная схема Исходные данные Погонная нагрузка Радиус оболочки Толщина оболочки Ширина шпангоута Толщина шпангоута Материал оболочки: марка ВТ6С (О); коэффициент Пуассона модуль Юнга Выполнение расчёта Расчётная схема 1. Шпангоуты абсолютно жёсткие Определим цилиндрическую жёсткость оболочки
Вычислим коэффициент затухания
Определим силу взаимодействия
Определим перерезывающую силу
Определим погонный изгибающий момент
Погонный изгибающий момент
где Принимаем Так как область существования гармонической функции
Результаты расчёта заносим в таблицу 1 и вычерчиваем график функции С использованием графика
Расчётная схема 2. Расчёт подкреплённой оболочки с податливыми (упругими) шпангоутами Найдём площадь поперечного сечения шпангоута
Определим коэффициент податливости шпангоута
Погонный изгибающий момент по длине оболочки
Результаты вычислений заносим в таблицу 1 и строим график функции
Определим в процентах снижение величины изгибающего момента
Таблица 1
2. ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПОЛУСФЕРИЧЕСКОЙ ОБОЛОЧКИ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ
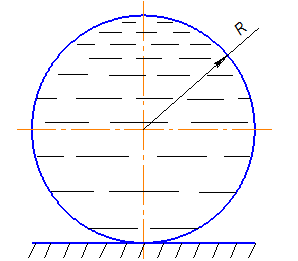
Условие задачи: Тонкостенный сосуд (рис.1), выполненный в виде полусферы, частично заполнен жидкостью. Закрепление оболочки по диаметру окружности – свободное. Цель расчета: 1. Построить эпюры погонных меридиональных 2. Определить толщину стенки оболочки, без учёта её собственного веса.
Исходные данные: Радиус сферы: Угол зеркала жидкости: Плотность жидкости (горючее): Коэффициент безопасности Материал оболочки: Марка ВТ6С (О); предел прочности Выполнение расчёта 1. Расчёт участка оболочки над уровнем жидкости Рассмотрим участок оболочки 1.1 Определяем границы участка BC: 1.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
где 1.3 Определяем высоту столба жидкости в полусферической оболочке:
1.4 Находим объём шарового сегмента, заполненного жидкостью:
1.5 Вычисляем вес жидкости по формуле:
1.6 Определяем текущий радиус кольцевого сечения оболочки:
1.7 Находим погонное меридиональное усилие
1.8 Определяем погонное кольцевое усилие
где
Для сферы R1
= R2
и для участка Результаты расчёта заносим в таблицу 1
при условии Таблица 1
2. Расчёт участка оболочки под уровнем жидкости Рассмотрим участок оболочки
2.1 Определим границы участка 2.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
где 2.3 Определяем составляющие уравнения равновесия: Объём шарового сегмента:
где Вес жидкости: Давление жидкости на уровне
Площадь поперечного сечения
где Значения составляющих уравнения равновесия заносим в таблицу 2. Таблица 2
2.4 Подставим найденные значения
2.5 Получим выражение для погонного кольцевого усилия
R 1 = R 2 = R ,
Результаты расчёта заносим в таблицу 3
при условии
Таблица 3
По данным таблиц строим эпюры погонных усилий. Схема эпюры приведена на рис. 4. С помощью эпюры определяем наиболее напряжённое сечение оболочки и максимальные усилия
3. Определение толщины стенки оболочки 3.1 Найдём допускаемое напряжение материала оболочки:
3.2 Определим толщину стенки:
3. ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ
Условие задачи:
Построить эпюры безмоментных напряжений Исходные данные: Радиус оболочки: Плотность жидкости (окислитель):
Толщина стенки оболочки:
Рис. 1. Схема оболочки Выполнение расчёта 1. Выводы расчётных зависимостей для верхней полусферы В верхней полусфере отсечём часть оболочки нормальным коническим сечением с углом
где вертикальную ось. Жидкость действует на стенку оболочки переменным давлением. Равнодействующую сил давления жидкости на вертикальную ось определим по формуле:
где
где Рис. 2. Расчётная схема Получаем:
Из уравнения равновесия после подстановки выражения для силы
Отсюда меридиональное напряжение:
Определим кольцевое напряжение
где После подстановки в уравнение Лапласа
Принимая угол Таблица 1
2. Выводы расчётных зависимостей для нижней полусферы
Рис. 3. Расчётная схема Отсечём нормальным коническим сечением часть сферы (рис. 3). Вес жидкости в объёме шарового сегмента
где
После подстановки получим:
Отсюда имеем:
Для нижней части полусферы
Отсюда:
Принимая угол Таблица 2
Выводы В опорной точке сферы безмоментные напряжения обращаются в бесконечность. Это является следствием обращения в ноль площади сечения, по которой действуют напряжения
Рис. 4. Эпюра напряжений 4. РАСЧЁТ СФЕРИЧЕСКОГО ТОПЛИВНОГО БАКА С ОПОРОЙ ПО ЭКВАТОРУ
Условие задачи: Сферический топливный бак с опорой по экватору, заполненный жидкостью, находится под давлением наддува (рис.1, рис. 2). Цель расчёта: Определить толщину стенки и массу конструкции бака при заданных размерах и нагрузке.
Исходные данные: Радиус оболочки: Плотность жидкости (горючее): Давление наддува: Уровень жидкости: Коэффициент осевой перегрузки: Коэффициент безопасности: Материал оболочки: марка ВТ6С (О); предел прочности плотность Примечание:
Для упрощения принимаем: Выполнение расчёта 1. Расчёт оболочки над опорой Формулы для расчёта погонных меридиональных
где
Принимая угол Таблица 1
2. Расчёт оболочки под опорой Выведем расчётные формулы для погонных меридиональных и кольцевых усилий от действия давления жидкости и давления наддува под опорой топливного бака
где
Давление
где h – высота столба жидкости от зеркала жидкости до расчётного сечения.
где Определим вес жидкости в шаровом сегменте: где
Спроектируем погонные меридиональные усилия Величина равнодействующей
Окончательно получаем Принимая угол Таблица 2
Подставляем полученные выражения Получаем формулу для вычисления погонных меридиональных усилий:
Подставляя полученное выражение
где Для сферического бака R 1 = R 2 = R , поэтому уравнение Лапласа принимает вид:
Подставив выражение
Принимая угол Таблица 3
Погонные усилия в сферическом баке принимают наибольшее значение в нижнем полюсе. Кроме того, в нижнем полюсе Определение толщины стенки бака
Расчёт на прочность производим по максимальным погонным усилиям. Определяем напряжения в нижнем полюсе бака: где Подставив в эти формулы выражения для погонных меридиональных и кольцевых усилий, получим:
Минимальную толщину оболочки можно получить по формуле:
где Определяем массу оболочки бака:
где
Построим эпюру погонных усилий
Рис. 3. Эпюра погонных усилий
5. РАСЧЁТ БАКА НА ПРОЧНОСТЬ
Условие задачи:
Цилиндрический бак с верхним полуэллиптическим и нижним полусферическими днищами (рис.1) находится под действием давления наддува Цель расчёта: 1. Определить величину безмоментных напряжений 2. Определить толщину обечайки и днищ бака. Исходные данные: Радиус бака: Размеры эллиптического днища:
Высота столба жидкости: Плотность жидкости (окислитель): Давление наддува: Коэффициент безопасности: Материал оболочки: марка ВТ6С (О); предел прочности
Выполнение расчёта Участок верхнего эллиптического днища
Рис. 2. Схема эллиптического днища В днище нормальным коническим сечением I
–
I
отсечём верхнюю часть оболочки и составим для неё уравнение равновесия. Выбираем оси координат так, как показано на рис. 2. Из уравнения равновесия и уравнения Лапласа получаем выражения для
где
где x, y – координаты точки в рассматриваемом сечении оболочки. Для построения эпюр задаёмся значениями x. Координату y определяем из уравнения эллипса
Меньшую полуось b разбиваем на 5 равных частей, для каждого сечения производим расчёты, результаты расчётов заносим в таблицу 1. Таблица 1
Участок цилиндра над зеркалом жидкости Рис. 3. Сечение II – II Нормальным сечением к оси бака II – II отсечём часть цилиндра, расположенную над зеркалом жидкости (рис. 3). Составим уравнение равновесия для верхней отсеченной части оболочки в проекции на вертикальную ось:
Отсюда меридиональное напряжение:
Для цилиндра
Участок цилиндра под зеркалом жидкости
Рис. 4. Сечение III – III Для сечения III – III расчётная схема (рис. 4) будет отличаться от показанной на рис. 3 тем, что здесь необходимо дополнительно учесть давление на стенку цилиндрической части бака со стороны жидкости. Уравнение равновесия в проекции на вертикальную ось бака остаётся без изменений:
Поэтому меридиональное напряжение не меняется:
Окружное напряжение определяем из уравнения Лапласа
где Отсюда Участок нижнего полусферического днища
Рис. 5. Сечение IV – IV Для нижнего днища нормальным коническим сечением IV
–
IV
с углом
где r
– радиус кольцевого сечения оболочки, S
– площадь поперечного сечения,
G
– вес жидкости в объёме шарового сегмента, Vc
– объём шарового сегмента, Подставляя значения r
,
S
,
Уравнение Лапласа для сферической оболочки имеет вид:
Подставляя в уравнение Лапласа
Построим таблицу 2
значений Таблица 2
По полученным напряжениям в характерных сечениях бака строим эпюры напряжений Определение толщины стенок бака Для определения толщины днищ и обечайки бака используем следующее условие: σ
max
≤ [σ
], где [σ
] = Толщина стенки Получаем: для верхнего днища для обечайки бака для нижнего днища Из расчётов видно, что δ max = δ 2 = 0,518 мм – окончательная толщина стенки бака. По расчётной толщине стенки подбираем толщину листа согласно ГОСТ 22178 – 76:
Рис.6. Эпюры безмоментных напряжений Список литературы 1. Расчёт безмоментных оболочек: Методические указания по дисциплине “Основы расчёта оболочек” для специальностей: 130600-Ракетостроение, 130400-Ракетные двигатели/ Сост. Л.И. Гречух, И. Н. Гречух.- Омск: Изд-во ОмГТУ, 2002.- 32 с. |

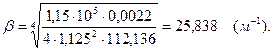







 ,
,
 .
.
 - вес жидкости в объёме шарового сегмента.
- вес жидкости в объёме шарового сегмента.


 ;
;  ,
, .
. .
.

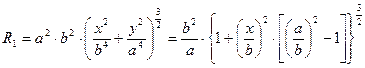 ,
, ,
, .
.


 .
.