| БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра радиотехнических систем
РЕФЕРАТ
На тему:
«Параметры кодов. Контроль, обнаружение и исправление ошибок»
МИНСК, 2008
1.
Параметры кодов
Определение 1.
Код – это множество дискретных сигналов, выбранное для передачи сообщений. Коды характеризуются следующими параметрами:
1
Основание кода 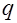 – число элементов множества – число элементов множества 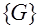 , выбранное для построения кода. Например, если: , выбранное для построения кода. Например, если:
а)
 , то , то  для троичного кода; для троичного кода;
б)
  для двоичного кода. для двоичного кода.
Практически  . .
Замечание – Эффективность каналов передачи (хранения) информации возрастает с переходом на недвоичные коды.
2
Длина кода  (значность) – число символов кодового слова. (значность) – число символов кодового слова.
Определение 2.
Последовательности элементов (символов) длиной  называются кодовыми словами или кодовыми векторами. Говорят, что слово называются кодовыми словами или кодовыми векторами. Говорят, что слово
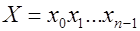 имеет длину
имеет длину  ; ;  , , 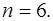
Параметр  определяет следующие особенности класса кодов. Коды бывают: определяет следующие особенности класса кодов. Коды бывают:
а)
равномерные (блоковые), 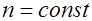 ; ;
б)
неравномерные,  ; ;
в)
бесконечные, 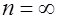 . К бесконечным относят коды: . К бесконечным относят коды:
1) свёрточные;
2) цепные;
3) непрерывные.
У равномерных (блоковых) кодов поток данных разделяется на блоки по 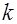 информационных символов, и далее они кодируются информационных символов, и далее они кодируются  – символьными кодовыми словами. – символьными кодовыми словами.
Для непрерывного кода поток данных разбивается на блоки длины 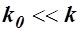 , которые называются кадрами информационных символов. Эти кадры кодируются , которые называются кадрами информационных символов. Эти кадры кодируются 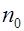 символами кодового слова (кадрами кодового слова). При этом кодирование каждого кадра информационных символов в отдельные кадры кодового слова производится с учетом предыдущих символами кодового слова (кадрами кодового слова). При этом кодирование каждого кадра информационных символов в отдельные кадры кодового слова производится с учетом предыдущих 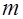 кадров информационных символов. кадров информационных символов.
На рисунке 1.1 показаны структуры кодирования блоковыми и непрерывными кодами.
k-битовый n-битовый n-битовый k-битовый
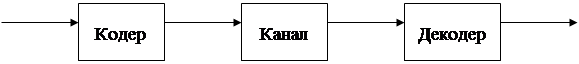 блок блок блок блок блок блок блок блок
Блоковый код
k0
битов/кадр n0
битов/кадр n0
битов/кадр k0
битов/кадр
Непрерывный код
Рисунок 1.1
3
Размерность кода 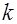 – число информационных позиций кодового слова. – число информационных позиций кодового слова.
4
Мощность кода 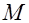 – число различных кодовых последовательностей (комбинаций), используемых для кодирования. – число различных кодовых последовательностей (комбинаций), используемых для кодирования.
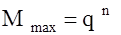 – максимальное число кодовых комбинаций при заданных – максимальное число кодовых комбинаций при заданных 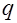 и и  . Например, . Например, 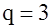 ; ; 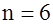 ; ;  . .
Определение 3.
Код, у которого используются все комбинации, называется полным (безизбыточным).
Определение 4.
Если число кодовых слов кода  , то код называется избыточным.
, то код называется избыточным.
Пример
– Пусть  , , 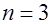 , , 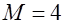 . .
Код   – избыточный; – избыточный; 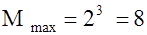 . .
5
Число проверочных (избыточных) позиций кодового слова 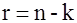 . .
Пусть 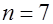 , ,  , ,  . Тогда на длине слова из семи символов – три избыточных. . Тогда на длине слова из семи символов – три избыточных.
6
Скорость передачи кода  . Для приведенного примера . Для приведенного примера  . .
7
Кратность ошибки 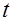 . Параметр . Параметр 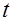 указывает, что все конфигурации из указывает, что все конфигурации из 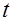
или менее ошибок в любом кодовом слове могут быть исправлены.
8
Расстояние Хэмминга между двумя векторами (степень удаленности любых кодовых последовательностей друг от друга) 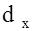 . .
Определение 5.
Если 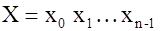 и и 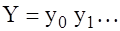  кодовые векторы, то расстояние Хэмминга равно числу позиций, в которых они различаются. Может обозначаться и как – кодовые векторы, то расстояние Хэмминга равно числу позиций, в которых они различаются. Может обозначаться и как –  . Например, . Например,  ; ;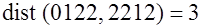 . .
Замечание – С позиции теории кодирования 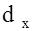 показывает, сколько символов в слове надо исказить, чтобы перевести одно кодовое слово в другое. показывает, сколько символов в слове надо исказить, чтобы перевести одно кодовое слово в другое.
9
Кодовое расстояние (минимальное расстояние кода) 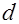 . .
Определение 6.
Наименьшее значение расстояния Хэмминга для всех пар кодовых последовательностей кода называют кодовым расстоянием.  , где , где 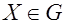 ; ;  ; ; 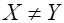 . .
Определение 7.
Код значности  , размерности , размерности 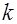 и расстояния и расстояния 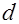 называется называется 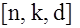 - кодом. - кодом.
Пример
– Можно построить следующий код:
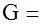  ; ;  ; ;  ; ;  . .
Данный код можно использовать для кодирования 2–битовых двоичных чисел,
используя следующее (произвольное) соответствие:

Найдем кодовое расстояние этого кода:
 ; ;
 ; ;
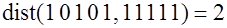 ; ;
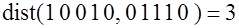 ; ;
 ; ;
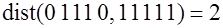 . .
Следовательно, для этого кода  . .
Замечание – 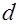 характеризует корректирующую способность кода характеризует корректирующую способность кода  . .
10
Вес Хэмминга вектора 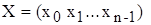 равен числу ненулевых позиций равен числу ненулевых позиций  , обозначается , обозначается 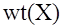 . Например, . Например, 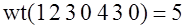 . .
Используя определение веса Хэмминга, получим очевидное выражение 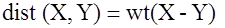 (1.1) (1.1)
Пример
–  ; ;
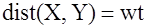    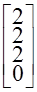 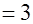 . . Из выражения (1.1) следует, что минимальное расстояние Хэмминга равно 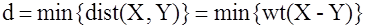 , где , где 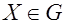 ; ; 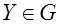 ; ;  . .
Замечание – Для нахождения минимального расстояния линейного кода не обязательно сравнивать все возможные пары кодовых слов. Если 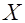 и и  принадлежат линейному коду принадлежат линейному коду 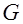 , то , то 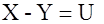 – также является кодовым словом кода – также является кодовым словом кода 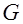 . Такой код является аддитивной группой (определена операция сложения) и, следовательно, . Такой код является аддитивной группой (определена операция сложения) и, следовательно, 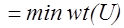 , где , где 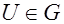 и и  , т.е. справедлива теорема. , т.е. справедлива теорема.
Теорема 1.
Минимальное расстояние линейного кода равно минимальному весу ненулевых кодовых слов.
Т.к. 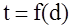 , то возникает вопрос о величине , то возникает вопрос о величине  , такой, чтобы код обеспечивал контроль ошибок, т.е. обнаружение и исправление ошибок. , такой, чтобы код обеспечивал контроль ошибок, т.е. обнаружение и исправление ошибок.
2 Контроль ошибок
Кодовое слово можно представить в виде вектора с координатами в 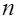 – мерном векторном пространстве. Например, для – мерном векторном пространстве. Например, для 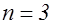 вектор вектор  находится в трёхмерном евклидовом пространстве, рисунок 1.2. Разрешенными для передачи выбраны вектора находится в трёхмерном евклидовом пространстве, рисунок 1.2. Разрешенными для передачи выбраны вектора  и и 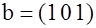 . .
 X0 X0
1 0 0 1 1 0
1 0 1 1 1 1
0 0 0 0 1 0 X1
0 0 1 0 1 1
X2
Рисунок 1.2
Рисунок дает наглядную алгебраическую интерпретацию понятия “мощность кода”:
а)
кодовые слова полного кода определяют  – мерное пространство, состоящее из – мерное пространство, состоящее из  последовательностей ( последовательностей ( – трехмерное пространство, состоящее при – трехмерное пространство, состоящее при  из 8 последовательностей полного кода); из 8 последовательностей полного кода);
б)
кодовые слова избыточного кода определяют подпространство (подмножество)  – мерного пространства, состоящее из – мерного пространства, состоящее из 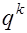 последовательностей. последовательностей.
Под воздействием помех происходит искажение отдельных разрядов слова. В результате разрешённые для передачи кодовые векторы переходят в другие векторы (с иными координатами) – запрещённые. Факт перехода разрешённого слова в запрещённое для передачи слово можно использовать для контроля за ошибками.
Возможна ситуация, когда разрешённый вектор переходит в другой разрешённый кодовый вектор: 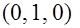  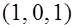 . В этом случае ошибки не обнаруживаются, и контроль становится неэффективным. . В этом случае ошибки не обнаруживаются, и контроль становится неэффективным.
Из рассмотренной модели можно сделать следующий важный вывод: для
того чтобы передаваемые векторы можно было бы отличать друг от друга при наличии помех, необходимо располагать эти векторы в  – мерном пространстве – мерном пространстве
как можно дальше друг от друга. Из этой же  – мерной модели следует геометрическая интерпретация расстояния Хэмминга: – мерной модели следует геометрическая интерпретация расстояния Хэмминга: 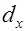 – это число рёбер, которые нужно пройти, чтобы перевести один вектор в другой, т.е. попасть из вершины одного вектора в вершину другого. – это число рёбер, которые нужно пройти, чтобы перевести один вектор в другой, т.е. попасть из вершины одного вектора в вершину другого.
2.1 Обнаружение и исправление ошибок
Стратегия обнаружения заключается в следующем. Декодер обнаруживает ошибку при априорном условии, что переданным словом было ближайшее по расстоянию к принятому слову. Покажем применение этого утверждения.
Пример
1
. Пусть  ; ;  . Разрешенным для передачи является множество кодовых слов: . Разрешенным для передачи является множество кодовых слов:
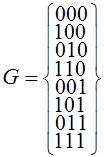 . .
Очевидно, что код 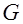 имеет имеет  . Любая одиночная ошибка трансформирует данное кодовое слово в другое разрешенное слово. Это случай безизбыточного кода, не обладающего корректирующей возможностью. . Любая одиночная ошибка трансформирует данное кодовое слово в другое разрешенное слово. Это случай безизбыточного кода, не обладающего корректирующей возможностью.
Пример
2.
Пусть теперь подмножество 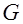 разрешённых кодовых слов предоставлено в виде двоичных комбинаций с чётным числом единиц. разрешённых кодовых слов предоставлено в виде двоичных комбинаций с чётным числом единиц.
 . .
Заданный код 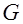 имеет имеет 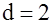 . Запрещенные кодовые слова представлены в виде подмножества . Запрещенные кодовые слова представлены в виде подмножества  : :
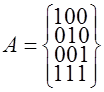 . .
Если 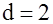 , то ни одно из разрешенных кодовых слов (т.е. кода , то ни одно из разрешенных кодовых слов (т.е. кода 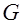 ) при одиночной ошибке не переходит в другое разрешённое слово этого же кода. Таким образом, код ) при одиночной ошибке не переходит в другое разрешённое слово этого же кода. Таким образом, код 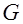 обнаруживает: обнаруживает:
– одиночные ошибки;
– ошибки нечетной кратности (для 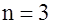 - тройные). - тройные).
Например, тройная ошибка кодового слова 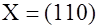 ; ;  , переводит его в запрещенный вектор , переводит его в запрещенный вектор 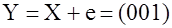 . .
Вывод – В общем случае, при необходимости обнаруживать ошибки кратности  кодовое расстояние кода должно быть кодовое расстояние кода должно быть
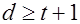 . .
Пример
3
. Пусть  ; ; 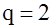 ; код ; код 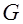 задан векторами задан векторами  и и 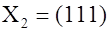 . .
При возникновении одиночных ошибок или множества векторов
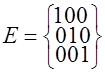
кодовому слову 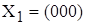 соответствует следующее запрещенное подмножество соответствует следующее запрещенное подмножество 
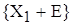 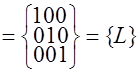 .
Кодовому слову .
Кодовому слову 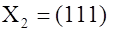 соответствует запрещенное подмножество соответствует запрещенное подмножество  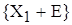 = = = =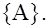
Таким образом, коду 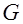 – разрешенному для передачи подмножеств векторов соответствует два запрещенных подмножества векторов – разрешенному для передачи подмножеств векторов соответствует два запрещенных подмножества векторов 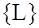 и и  : :
  = =
 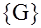 = =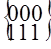 . .
 = =
Стратегия исправления ошибок заключается в следующем:
– каждая из одиночных ошибок приводит к запрещенному кодовому слову того или иного запрещенного подмножества ( и и  ); );
– структура кодового запрещенного подмножества, относящаяся к соответствующему исходному разрешенному подмножеству, позволяет определить местоположение ошибки, т.е. исправить ошибку.
Для исправления ошибок кратности  кодовое расстояние должно удовлетворять соотношению кодовое расстояние должно удовлетворять соотношению 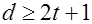 . (1.2) . (1.2)
Используя эту формулу, можно записать
 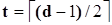 , ,
где  обозначает целую часть числа обозначает целую часть числа 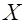 . .
Замечание – Существуют модели каналов (например, канал с дефектами), в которых величина  может быть больше, чем в выражении (1.2). может быть больше, чем в выражении (1.2).
ЛИТЕРАТУРА
· Митюхин А.И., Игнатович В.Г. Линейные групповые коды: Учеб. пособие. – Мн. :БГУИР, 2002.
· Митюхин А.И. Элементы абстрактной алгебры: Учеб.пособие. – Мн.: БГУИР, 2000.
· Лосев В.В. Помехоустойчивое кодирование в радиотехнических системах передачи информации: Метод. Пособие Ч.1. Линейные коды. – Мн.: ВШ, 2004.
|