| ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ЭКОНОМИКИ И ВНЕШНЕЭКОНОМИЧЕСКИХ СВЯЗЕЙ
Контрольная работа
по дисциплине: «Линейная алгебра»
Выполнил:
Воропаева Екатерина Андреевна
(Ф.И.О.)
2010-З-ФК-1
(номер группы)
Вариант № 3
Проверил
преподаватель:
Кирютенко Юрий Александрович
Ростов – на - Дону
2010
Оглавление
1. Комплексные числа. 3
2. Элементы аналитической геометрии. 3
3. Вычисление определителей. 3
4. Метод Гаусса. 3
5. Метод Крамера. 3
6. Матричные уравнения. 3
Решение контрольной работы
Вариант № 3
1.3. а) Вычислите:
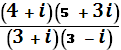 . .
Решение:
Используя следующие правила:
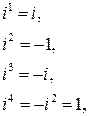 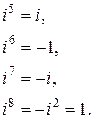
выполним вычисления
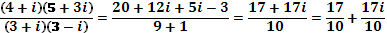
1.3. б) Решите уравнение:
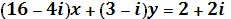 , ,
где 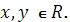
Решение:
Левую часть уравнения можно рассматривать, как некоторое неизвестное комплексное число. Приведя его к виду 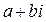 , получаем уравнение равносильное данному: , получаем уравнение равносильное данному: 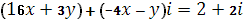 . Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе: . Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе:
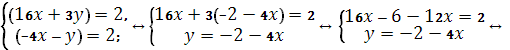
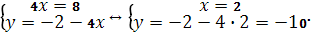
Ответ
: 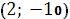 . .
Треугольник 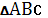 задан координатами вершин на плоскости. Найти уравнения сторон треугольника, медианы ВМ и высоты СН. задан координатами вершин на плоскости. Найти уравнения сторон треугольника, медианы ВМ и высоты СН.
A
(1,7); В
(-3,-1); С
(4,-2).
Решение:
Выполним чертеж:

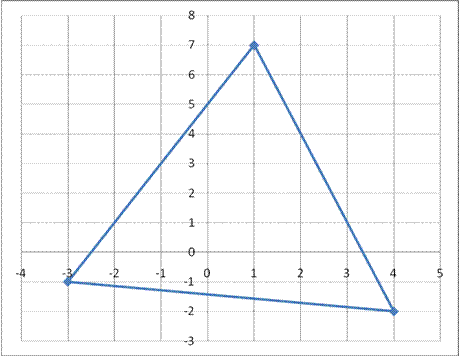 Для нахождения уравнений сторон треугольника воспользуемся формулой уравнения прямой, проходящей через две точки А1
(x1
, y1
) и
А2
(x2
, y2
):
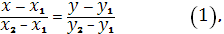
подставив поочередно в формулу (1) попарно координаты точек А
и В
, В
и С
, А
и С
.
Уравнение прямой, проходящей через точки А
(1, 7) и В
(-3, -1):
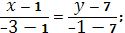
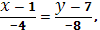
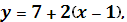
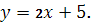
Уравнение прямой, проходящей через точки В
(-3, -1)
b
C
(
4,-2)
:
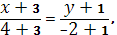
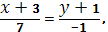
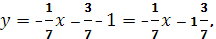
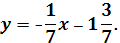
Уравнение прямой, проходящей через точки А
(1, 7) и
C
(
4,-2):
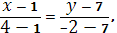
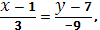
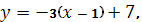
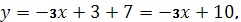
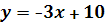
Для определения уравнения медианы ВМ предварительно вычислим координаты точки М, воспользовавшись формулами нахождения координат середины отрезка А1
А2
(А1
(x1
, y1
) и А2
(x2
, y2
)):
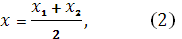
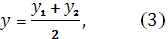
где х1
, у1
– координаты точки А
(1, 7);
х2
, у2
– координаты точки С
(4, -2).
Координаты точки М:
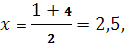
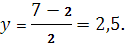
Точка М имеет координаты х = 2,5
и у = 2,5
, т. е. М
(2,5; 2,5).
Для нахождения уравнения медианы ВМ воспользуемся формулой (1), подставив в нее координаты точек В
(-3, -1)
и М
(2,5; 2,5)
.
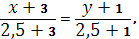
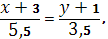
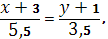
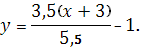
Уравнение медианы ВМ:
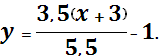
Для определения уравнения высоты СН воспользуемся формулой уравнения прямой, проходящей через данную точку М1
(
x
1
,
y
1
)
перпендикулярно к данной прямой y
=
ax
+
b
:
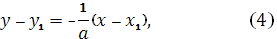
подставив в нее координаты точки С(
4,-2
)
и данные из уравнения прямой АВ 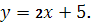 Получим: Получим:
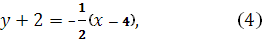
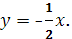
Уравнение высоты СН:
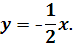
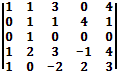
Решение:
Используя алгебраические преобразования, получим в первом столбце в четвертой и пятой строке нули. Для этого от элементов четвертой строки отнимем элементы первой строки и полученный результат запишем на место элементов четвертой строки матрицы. От элементов пятой строки отнимем элементы первой строки и полученный результат запишем на место элементов пятой строки матрицы. Получим:
  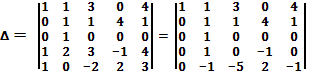
Разложим определитель матрицы по элементам первого столбца, имеем:
  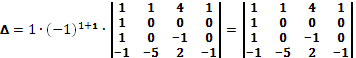
Такой прием называется сведением определителя более высокого порядка к определителю более низкого порядка.
Во второй строке последнего определителя все элементы строки, кроме элемента первого столбца, равны нулю. Поэтому удобно разложить определитель матрицы по элементам второй строки. В результате получим следующий результат.
  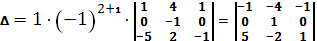
В новом определителе третьего порядка во второй строке только один элемент не равен нулю, поэтому разложим этот определитель по элементам второй строки. Получим следующий результат:
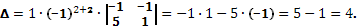
Определитель матрицы равен 4.
Найти решение системы линейных уравнений методом Гаусса.
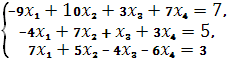
Решение:
Система уравнений
– это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Решением системы уравнений
называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.
Метод Гаусса
– классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Сформируем исходную матрицу:
| х1
|
х2
|
х3
|
х4
|
Столбец свободных членов
|
| 7
|
5
|
-4
|
-6
|
3
|
| -4
|
7
|
1
|
3
|
5
|
| -9
|
10
|
3
|
7
|
7
|
Разделим все элементы первой строки матрицы на 7, получим:
| х1
|
х2
|
х3
|
х4
|
Столбец свободных членов
|
| 1
|
5/7
|
- 4/7
|
- 6/7
|
3/7
|
| -4
|
7
|
1
|
3
|
5
|
| -9
|
10
|
3
|
7
|
7
|
Умножим все элементы первой строки матрицы на 4 и просуммируем с элементами второй строки, результат вычислений запишем во вторую строку:
| х1
|
х2
|
х3
|
х4
|
Столбец свободных членов
|
| 1
|
5/7
|
- 4/7
|
- 6/7
|
3/7
|
| 0
|
9 6/7
|
-1 2/7
|
- 3/7
|
6 5/7
|
| -9
|
10
|
3
|
7
|
7
|
Умножим все элементы первой строки матрицы на 9 и просуммируем с элементами третьей строки, результат вычислений запишем в третью строку:
| х1
|
х2
|
х3
|
х4
|
Столбец свободных членов
|
| 1
|
5/7
|
- 4/7
|
- 6/7
|
3/7
|
| 0
|
9 6/7
|
-1 2/7
|
- 3/7
|
6 5/7
|
| 0
|
16 3/7
|
-2 1/7
|
- 5/7
|
10 6/7
|
Все элементы второй строки разделим на 9 6/7:
| х1
|
х2
|
х3
|
х4
|
Столбец свободных членов
|
| 1
|
5/7
|
- 4/7
|
- 6/7
|
3/7
|
| 0
|
1
|
- 3/23
|
- 1/23
|
47/69
|
| 0
|
16 3/7
|
-2 1/7
|
- 5/7
|
10 6/7
|
Все элементы второй строки умножим на -16 3/7 и складываем с элементами третьей строки:
| х1
|
х2
|
х3
|
х4
|
Столбец свободных членов
|
| 1
|
5/7
|
- 4/7
|
- 6/7
|
3/7
|
| 0
|
1
|
- 3/23
|
- 1/23
|
47/69
|
| 0
|
0
|
0
|
0
|
- 1/3
|
Ранг матрицы системы равен: r(A) = 2; ранг расширенной матрицы (вместе со столбцом свободных членов) r(A1
)=3, т. е. r(A)≠r(A1
); следовательно система уравнений несовместна, т. е. не имеет решений.
Решить систему линейных уравнений методом Крамера.
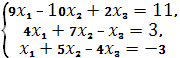
Решение:
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
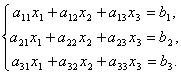
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем
системы.
Составим ещё три определителя следующим образом: заменим в определителе 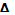 последовательно 1, 2 и 3 столбцы столбцом свободных членов последовательно 1, 2 и 3 столбцы столбцом свободных членов
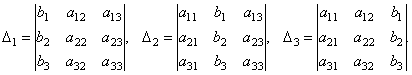
Тогда можно доказать следующий результат.
Теорема (правило Крамера).
Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
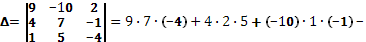
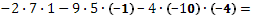 - 331 - 331
Определитель системы не равен нулю, следовательно, система уравнений имеет единственное решение.
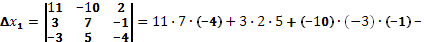
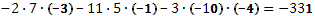
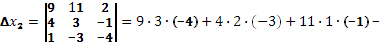
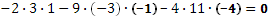
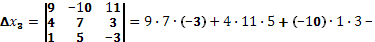
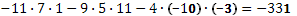
Найдем решение системы уравнений:
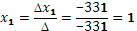
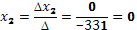
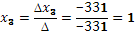
Решить матричное уравнение, вычисляя обратную матрицу, сделать проверку.
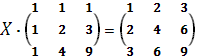
Решение:
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
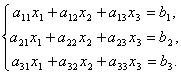
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов
 . .
Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
 или короче A∙X=B. или короче A∙X=B.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением
.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:
 . .
Поскольку A-1
A = E
и E
∙X = X
, то получаем решение матричного уравнения в виде X = A-1
B
.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных
. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A
не будет квадратной и поэтому нельзя найти решение системы в виде X = A-1
B
.
В нашем случае матричная запись системы уравнений будет выглядеть следующим образом: X∙A=B, а решение матричного уравнения получаем в виде X = B∙ A-1
.
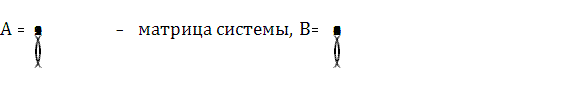
Вычислим обратную матрицу А-1
.
Определитель матрицы
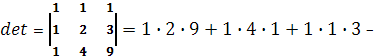
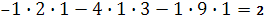
Система совместна и имеет единственное решение.
Вычислим союзную матрицу, состоящую из алгебраических дополнений элементов матрицы А.
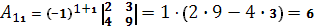
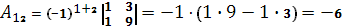
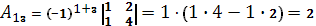
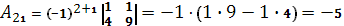
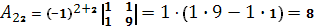
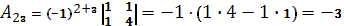
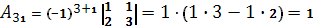
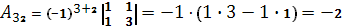
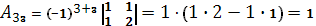
Союзная матрица  . .
Транспонируя союзную матрицу, находим к матрице А присоединенную матрицу.
Присоединенная матрица 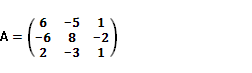 . .
Вычислим обратную матрицу по формуле: 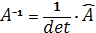 . Получим следующий результат: . Получим следующий результат:
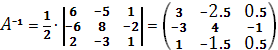 . .
Найдем X
=
B
∙
A
-1
, выполнив умножение матриц B∙ A-1
.
Матрица - математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами.
Умножение матриц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения называется произведением матриц. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором, в этом случае говорят, что форма матриц согласована.
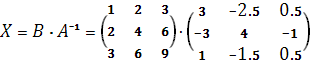
Вычислим элементы матрицы |Х|:
x1,1
= b1,1
∙ a1,1
+ b2,1
∙ a1,2
+ b3,1
∙ a1,3
x1,2
= b1,2
∙ a1,1
+ b2,2
∙ a1,2
+ b3,2
∙ a1,3
x1,3
= b1,3
∙ a1,1
+ b2,3
∙ a1,2
+ b3,3
∙ a1,3
x2,1
= b1,1
∙ a2,1
+ b2,1
∙ a2,2
+ b3,1
∙ a2,3
x2,2
= b1,2
∙ a2,1
+ b2,2
∙ a2,2
+ b3,2
∙ a2,3
x2,3
= b1,3
∙ a2,1
+ b2,3
∙ a2,2
+ b3,3
∙ a2,3
x3,1
= b1,1
∙ a3,1
+ b2,1
∙ a3,2
+ b3,1
∙ a3,3
x3,2
= b1,2
∙ a3,1
+ b2,2
∙ a3,2
+ b3,2
∙ a3,3
x3,3
= b1,3
∙ a3,1
+ b2,3
∙ a3,2
+ b3,3
∙ a3,3
| x1,1
=
|
1
|
∙
|
3
|
+
|
2
|
∙
|
(-3)
|
+
|
3
|
∙
|
1
|
=
|
3
|
+
|
(-6)
|
+
|
3
|
=
|
0
|
| x1,2
=
|
1
|
∙
|
(-2.5)
|
+
|
2
|
∙
|
4
|
+
|
3
|
∙
|
(-1.5)
|
=
|
-2.5
|
+
|
8
|
+
|
(-4.5)
|
=
|
1
|
| x1,3
=
|
1
|
∙
|
0.5
|
+
|
2
|
∙ (
|
-1)
|
+
|
3
|
∙
|
0.5
|
=
|
0.5
|
+
|
(-2)
|
+
|
1.5
|
=
|
0
|
| x2,1
=
|
2
|
∙
|
3
|
+
|
4
|
∙
|
(-3)
|
+
|
6
|
∙
|
1
|
=
|
6
|
+
|
(-12)
|
+
|
6
|
=
|
0
|
| x2,2
=
|
2
|
∙
|
(-2.5)
|
+
|
4
|
∙
|
4
|
+
|
6
|
∙
|
(-1.5)
|
=
|
-5
|
+
|
16
|
+
|
(-9)
|
=
|
2
|
| x2,3
=
|
2
|
∙
|
0.5
|
+
|
4
|
∙
|
(-1)
|
+
|
6
|
∙
|
0.5
|
=
|
1
|
+
|
(-4)
|
+
|
3
|
=
|
0
|
| x3,1
=
|
3
|
∙
|
3
|
+
|
6
|
∙
|
(-3)
|
+
|
9
|
∙
|
1
|
=
|
9
|
+
|
(-18)
|
+
|
9
|
=
|
0
|
| x3,2
=
|
3
|
∙
|
(-2.5)
|
+
|
6
|
∙
|
4
|
+
|
9
|
∙
|
(-1.5)
|
=
|
-7.5
|
+
|
24
|
+
|
(-13.5)
|
=
|
3
|
| x3,3
=
|
3
|
∙
|
0.5
|
+
|
6
|
∙
|
(-1)
|
+
|
9
|
∙
|
0.5
|
=
|
1.5
|
+
|
(-6)
|
+
|
4.5
|
=
|
0
|
Результирующая матрица: .
Выполним проверку, подставив в формулу X∙A=B значения │Х│ и │А│. В результате выполненного умножения матриц должна получится матрица │В│.
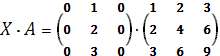
Вычислим элементы матрицы |B|:
b1,1
= x1,1
∙ a1,1
+ x1,2
∙ a2,1
+ x1,3
∙ a3,1
b1,2
= x1,1
∙ a1,2
+ x1,2
∙ a2,2
+ x1,3
∙ a3,2
b1,3
= x1,1
∙ a1,3
+ x1,2
∙ a2,3
+ x1,3
∙ a3,3
b2,1
= a2,1
∙ b1,1
+ a2,2
∙ b2,1
+ a2,3
∙ b3,1
b2,2
= a2,1
∙ b1,2
+ a2,2
∙ b2,2
+ a2,3
∙ b3,2
b2,3
= a2,1
∙ b1,3
+ a2,2
∙ b2,3
+ a2, 3
∙ b3,3
b3,1
= a3,1
∙ b1,1
+ a3,2
∙ b2,1
+ a3,3
∙ b3,1
b3,2
= a3,1
∙ b1,2
+ a3,2
∙ b2,2
+ a3,3
∙ b3,2
b3,3
= a3,1
∙ b1,3
+ a3,2
∙ b2,3
+ a3,3
∙ b3,3
| b1,1
=
|
0
|
∙
|
1
|
+
|
1
|
∙
|
1
|
+
|
0
|
∙
|
1
|
=
|
0
|
+
|
1
|
+
|
0
|
=
|
1
|
| b1,2
=
|
0
|
∙
|
1
|
+
|
1
|
∙
|
2
|
+
|
0
|
∙
|
4
|
=
|
0
|
+
|
2
|
+
|
0
|
=
|
2
|
| b1,3
=
|
0
|
∙
|
1
|
+
|
1
|
∙
|
3
|
+
|
0
|
∙
|
9
|
=
|
0
|
+
|
3
|
+
|
0
|
=
|
3
|
| b2,1
=
|
0
|
∙
|
1
|
+
|
2
|
∙
|
1
|
+
|
0
|
∙
|
1
|
=
|
0
|
+
|
2
|
+
|
0
|
=
|
2
|
| b2,2
=
|
0
|
∙
|
1
|
+
|
2
|
∙
|
2
|
+
|
0
|
∙
|
4
|
=
|
0
|
+
|
4
|
+
|
0
|
=
|
4
|
| b2,3
=
|
0
|
∙
|
1
|
+
|
2
|
∙
|
3
|
+
|
0
|
∙
|
9
|
=
|
0
|
+
|
6
|
+
|
0
|
=
|
6
|
| b3,1
=
|
0
|
∙
|
1
|
+
|
3
|
∙
|
1
|
+
|
0
|
∙
|
1
|
=
|
0
|
+
|
3
|
+
|
0
|
=
|
3
|
| b3,2
=
|
0
|
∙
|
1
|
+
|
3
|
∙
|
2
|
+
|
0
|
∙
|
4
|
=
|
0
|
+
|
6
|
+
|
0
|
=
|
6
|
| b3,3
=
|
0
|
∙
|
1
|
+
|
3
|
∙
|
3
|
+
|
0
|
∙
|
9
|
=
|
0
|
+
|
9
|
+
|
0
|
=
|
9
|
Результирующая матрица: . Как показывают расчет, задача решена верно.
|