| Задание 1
Раскрыть сущность экономико-математической модели. Привести классификацию экономико-математических моделей; дать понятие экономико-математического моделирования и рассмотреть его этапы.
С понятием «моделирование экономических систем» (а также математических и др.) связаны два класса задач:
задачи анализа, когда система подвергается глубокому изучению ее свойств, структуры и параметров, то есть исследуется предметная область будущего моделирования.
Задачи, связанные с задачами синтеза (получения ЭММ данной системы).
Модель
– изображение, представление объекта, системы, процесса в некоторой форме, отличной от реального существования.
Различают физическое и математическое моделирование.
Классификация моделей:
— вещественные
— символьные
— словесно-описательные
1. математические
2. аналитические
· имитационные
· структурные
= формальные
= функциональные
Этапы практического моделирования
1. Анализ экономической системы, ее идентификация и определение достаточной структуры для моделирования.
2. Синтез и построение модели с учетом ее особенностей и математической спецификации.
3. Верификация модели и уточнение ее параметров
4. Уточнение всех параметров системы и соответствие параметров модели, их необходимая валидация (исправление, корректирование).
Задание 3
В качестве примера построим модель оптимального размещения активов для некоторого гипотетического банка, работающего более двух лет, баланс которого приводится в таблицах ниже.
Пассив баланса
| Наименование статей баланса
|
Сумма, млн. руб.
|
Риск одновременного снятия, %
|
| Средства банков на корреспондентских счетах
|
5,1
|
25
|
| Кредиты и депозиты банков (включая НБ РБ)
|
| Кредитные ресурсы, полученные от других банков,
депозиты других банков до востребования
|
2,8
|
55
|
| Кредитные ресурсы, полученные от других банков,
и депозиты других банков с договорными сроками
|
3,4
|
0
|
| Средства клиентов
|
| Остатки на текущих (расчетных) счетах юридических и
физических лиц
|
196
|
25
|
| Вклады (депозиты) юридических и физических лиц:
|
| до востребования
|
5,8
|
25
|
| с договорными сроками
|
85
|
| Прочие пассивы
|
7,6
|
| Итого пассивов
|
305,7
|
| Собственный капитал банка
|
68
|
Актив баланса
| Наименование статей баланса
|
Сумма, млн. руб.
|
Доход-ность, %
|
Степень риска, %
|
Ликвид-ность, %
|
| Касса и приравненные к ней средства
|
х1
|
0
|
0
|
100
|
| Средства на корреспондентских счетах в банках
|
| Средства в НБ РБ
|
х2
|
0
|
0
|
100
|
| Средства в банках стран – членов ОЭСР до востребования
|
х3
|
5
|
30
|
75
|
| Средства в банках стран, не являющихся членами ОЭСР,
до востребования
|
х4
|
7
|
65
|
55
|
| Обязательные резервы в НБРБ
|
33,5
|
0
|
0
|
0
|
| Кредиты и депозиты банкам
|
| Кредиты банкам-резидентам РБ под обеспечение
государственных ценных бумаг РБ в бел. руб.
|
х5
|
32
|
0
|
100
|
| Депозиты в банках-резидентах РБ под гарантии НБ РБ
|
х6
|
25
|
0
|
100
|
| Кредиты юридическим и физическим лицам:
|
| обеспеченные залогом ценных бумаг, эмитированных
юридическими лицами
|
х7
|
38
|
100
|
0
|
| обеспеченные гарантийными депозитами в бел. руб. и СКВ
|
х8
|
33
|
0
|
0
|
| обеспеченные залогом имущества
|
х9
|
39
|
100
|
0
|
| обеспеченные гарантиями и поручительствами юридических лиц
|
х10
|
34
|
100
|
0
|
| Государственные ценные бумаги РБ, номинированные в бел. руб.
|
х11
|
25
|
0
|
100
|
| Основные средства и нематериальные активы
|
12,4
|
0
|
100
|
0
|
Запишем целевую функцию, в данной модели представляющую процентный доход банка от размещения активов, который следует максимизировать:
f(x)= 0,05х3
+ 0,07х4
+ 0,32х5
+ 0,25х6
+ 0,38х7
+ 0,33х8
+ 0,39х9
+
+ 0,34х10
+ 0,25х11
→max
Первое ограничение следует из условия баланса: сумма активных статей баланса должна быть равна сумме пассивных его статей + собственный капитал
х1
+ х2
+ х3
+ х4
+ 33,5 + х5
+ х6
+ х7
+ х8
+ х9
+ х10
+ х11
+ 12,4 = 373,7
Второе ограничение следует из норматива по достаточности капитала, при этом предположим, что R = 0

Третье ограничение следует из норматива мгновенной ликвидности, которое представляет собой отношение балансовых сумм активов и пассивов до востребования и с просроченными сроками:
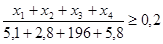
Четвертое ограничение следует из норматива краткосрочной ликвидности, которое представляет соотношение фактической и требуемой ликвидности:

Пятое ограничение запишем исходя из минимально допустимого значения соотношения ликвидных и суммарных активов баланса:

Шестое ограничение следует из ограниченности совокупной суммы крупных рисков.
Пусть х5
≥0,1Ч68 и х6
≥0,1Ч68, тогда
х5
+ х6
≤6Ч68
Седьмое ограничение следует из ограниченности средств, размещенных в банках стран — не членов ОЭСР
х4
≤68
Далее запишем ограничения, вытекающие из норматива максимального размера риска на одного клиента, считая для простоты, что одна статья баланса соответствует одному клиенту:
х3
≤0,25Ч68; х4
≤0,25Ч68; х5
≤0,25Ч68;
х6
≤0,25Ч68; х7
≤0,25Ч68; х8
≤0,25Ч68;
х9
≤0,25Ч68; х10
≤0,25Ч68
 В завершение напишем условие неотрицательности: В завершение напишем условие неотрицательности:
хj
≥ 0, j = 1,11
Таким образом, все вышеперечисленные ограничения представляют собой модель оптимального распределения активов банка с рассмотренным выше балансом.
Задание 4
Построить уравнение регрессии, описывающее зависимость прибыли банка (у) от объема межбанковских кредитов и депозитов (х), оценить ее качество и степень зависимости. С помощью построенной регрессии прогнозировать, какой будет средняя прибыль банка при достижении объема межбанковских кредитов и депозитов величины 53 млн. руб.
| № банка
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
| Кредиты и депозиты
|
18
|
23
|
28
|
29
|
34
|
36
|
37
|
42
|
44
|
45
|
49
|
50
|
| Прибыль
|
12
|
17
|
15
|
25
|
20
|
32
|
25
|
35
|
30
|
40
|
41
|
45
|
Решение
Информацию, представленную в исходных данных представим графически:

Из диаграммы рассеяния видно, что зависимость между прибылью банка и объемом межбанковских кредитов и депозитов носит линейный характер. Кроме того, исследуется зависимость прибыли банка только от одного фактора — объема межбанковских кредитов и депозитов, поэтому регрессию будем строить в виде
у = а + bх
т.е. это будет простая линейная регрессия. Для расчета ее параметров воспользуемся известными формулами:
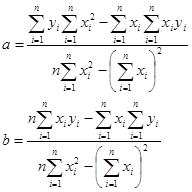
Для этого в рабочей таблице рассчитаем нужные суммы:
| i
|
xi
|
yi
|
xi
yi
|
xi
2
|
yi
2
|
| 1
|
18
|
12
|
216
|
324
|
144
|
| 2
|
23
|
17
|
391
|
529
|
289
|
| 3
|
28
|
15
|
420
|
784
|
225
|
| 4
|
29
|
25
|
725
|
841
|
625
|
| 5
|
34
|
20
|
680
|
1156
|
400
|
| 6
|
36
|
32
|
1152
|
1296
|
1024
|
| 7
|
37
|
25
|
925
|
1369
|
625
|
| 8
|
42
|
35
|
1470
|
1764
|
1225
|
| 9
|
44
|
30
|
1320
|
1936
|
900
|
| 10
|
45
|
40
|
1800
|
2025
|
1600
|
| 11
|
49
|
41
|
2009
|
2401
|
1681
|
| 12
|
50
|
45
|
2250
|
2500
|
2025
|
| ∑
|
435
|
337
|
13358
|
16925
|
10763
|
Подставим результаты, полученные в таблице в формулы:


Таким образом, уравнение регрессии, описывающее зависимость между прибылью банка и объемом межбанковских кредитов и депозитов, имеет вид:
у = –7,71 + 0,987х
Оценим качество построенной регрессии. Для этого рассчитаем коэффициент детерминации, используя формулу:

Значение коэффициента детерминации достаточно близко к единице, поэтому качество построенной регрессии хорошее. Можно утверждать, что изменение прибыли банка на 86,8% зависит от изменения межбанковских кредитов и депозитов, и на 13,2% – от прочих факторов.
Степень зависимости между исследуемыми показателями оценивается на основании коэффициента корреляции:

Коэффициент корреляции близок к единице, поэтому имеем достаточно сильную линейную зависимость между прибылью банка и объемом межбанковских кредитов и депозитов.
Так как качество построенной регрессии хорошее, ее можно использовать для прогнозирования. Подставим прогнозное значение хпр
= 53 в построенное уравнение регрессии:
упр
= –7,71 + 0,987Ч53 = 44,623 (млн. руб.)
Таким образом, если объем межбанковских кредитов и депозитов достигнет 53 млн. руб., то средняя прибыль коммерческого банка составит 44 млн. 623 тыс. руб.
Задание 5
За компаниями A, B и С проводились наблюдения в течение трех периодов. Данные в процентах приводятся в таблице ниже. Оценить ожидаемую доходность и риск каждой акции, на основании этих оценок дать сравнительную характеристику. Рассчитать ковариации доходностей акций друг с другом. Дать определение эффективного портфеля ценных бумаг и построить модели, позволяющие определить структуру эффективных портфелей.
| Период наблюдения
|
Доходность компании А
|
Доходность компании В
|
Доходность компании С
|
| 1
|
27
|
25
|
22
|
| 2
|
30
|
20
|
18
|
| 3
|
33
|
26
|
16
|
Решение
Оценим ожидаемую доходность каждой акции:
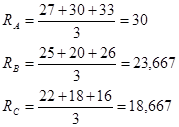
Оценим риск каждой акции, который выражается вариацией:

Из приведенных расчетов следует, что самыми привлекательными для инвестора ценными бумагами являются акции компании А, так как они имеют самую высокую ожидаемую доходность и наименьший риск. Если же сравнить между собой компании В и С, то акции компании В имеют несколько большую ожидаемую доходность, но и больший риск, поэтому выбор зависит от отношения инвестора к риску.
Рассчитаем ковариации доходностей акций друг с другом:
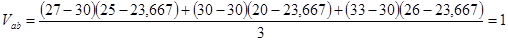

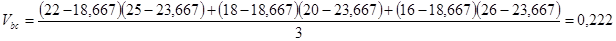
Из расчетов видно, что ковариация доходностей компаний А и С отрицательна, т.е. зависимость между доходностями акций этих компаний обратная, под воздействием одних и тех же факторов доходности меняются в разных направлениях. Ковариации доходностей акций компаний А и В, В и С положительные, что свидетельствует о прямой зависимости между доходностями акций этих компаний, под воздействием одних и тех же факторов доходности меняются в одном направлении.
Дадим определение эффективного портфеля. Портфель, имеющий минимальный риск при заданном уровне ожидаемой доходности или максимальную ожидаемую доходность при заданном уровне риска, называется эффективным.
пусть хА
, хВ
, хС
— доли капитала инвестора, вложенные в акции компаний А, В, С соответственно. Сумма долей равна единице, т.е.:
хА
+ хВ
+ хС
= 1
Так как риск портфеля, составленного из акций компаний А, В и С, выражается формулой:

а ожидаемая доходность этого же портфеля выражается формулой
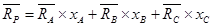
 то, подставляя рассчитанные значения вариаций, ковариаций, получаем модели, определяющие структуру эффективных портфелей: то, подставляя рассчитанные значения вариаций, ковариаций, получаем модели, определяющие структуру эффективных портфелей:
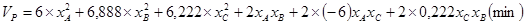
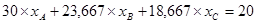
хА
+ хВ
+ хС
= 1
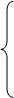 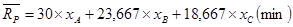
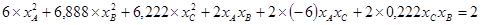
хА
+ хВ
+ хС
= 1
Задание 6
Руководство одного из банков решило разместить ресурсы в операциях с процентным арбитражем с целью получения прибыли от разницы процентных ставок на различных кредитных рынках с учетом изменения валютных курсов. Для проведения операций с процентным арбитражем на домашнем кредитном рынке было приобретено 500000 рос. руб. под 7,5% годовых на месяц. На момент начала операции наиболее привлекательными для банка оказались кредитный рынок США и еврорынок. Процентная ставка по вкладам на месяц на кредитном рынке США равнялась 7,75% годовых, а на еврорынке по вкладам в евро на месяц 7,7% годовых. Соотношение курсов валют было следующее: RUR/€ = 37,7 руб., RUR/$ = 27,8 руб. Через месяц на момент окончания операции прогнозируются следующие курсы валют: с вероятностью 0,4 RUR/€ = 36,3 руб., RUR/$ = 28,2 руб., с вероятностью 0,6 RUR/€ = 38,2 руб., RUR/$ = 26,6 руб. Определить наилучшую стратегию размещения ресурсов сроком на один месяц, используя критерии Вальда, Гурвица и Байеса.
Решение
В данной задаче выделяются 2 игрока: руководство банка, принимающее решения, и природа — рынок валют. Предположим, что руководство банка определило для себя три стратегии:
А1
— разместить 500000 руб. на еврорынке;
А2
— разместить 500000 руб. на рынке США;
А3
— разместить 250000 руб. на рынке США и 250000 руб. на еврорынке.
У природы будут две стратегии, соответствующие двум прогнозам курсов. Для определения наилучшей стратегии построим платежную матрицу. Ее размерность будет 3Ч2 в соответствии с количеством стратегий.
Элементы платежной матрицы будут равны прибыли, которую получит банк в каждой из возможных ситуаций.
Рассчитаем элемент платежной матрицы а 11
:
1. Конвертируем валюту:
500000/37,7 = 13262,6 €
2. Вкладываем получившуюся в валюте сумму на соответствующем рынке на месяц:
13262,6Ч(1+0,077/12) = 13347,7 €
3. Конвертируем полученную сумму в рубли соответственно стратегии природы:
13347,7Ч36,3 = 484,521 руб.
4. Рассчитаем сумму, которую нужно вернуть через месяц на домашнем рынке:
500000Ч(1+0,075/12) = 503125 руб.
5. Находим чистый доход от операции
484521,6 – 503125 = –18603,4 руб.
Аналогично рассчитываются все остальные элементы платежной матрицы. В результате расчетов она принимает вид:
| П1
|
П2
|
| A1
|
-18603,45
|
6757,18
|
| A2
|
7344,87
|
-21617,96
|
| A3
|
5629,29
|
7430,39
|
Для выбора лучшей стратегии воспользуемся следующими критериями:
1. Критерий Вальда — критерий крайнего пессимизма. Наилучшая, по Вальду, стратегия — соответствующая наибольшему из наименьших выигрышей. Наилучшей, по Вальду, будет стратегия А3
, т.е. разместив по 250000 тыс. руб. на рынках США и Европы, банк получит прибыль не менее, чем на 5629,29 руб.
2. Критерий Сэвиджа — критерий минимального риска. Наилучшей, по Сэвиджу, считается стратегия, соответствующая наименьшему из наибольших рисков. Для ее определения построим дополнительную матрицу R:
| П1
|
П2
|
| A1
|
25948,32
|
673,20
|
| A2
|
0,00
|
29048,34
|
| A3
|
1715,59
|
0,00
|
Стратегия А3
соответствует минимальному из максимальных рисков, т.е. наилучшей, по Сэвиджу будет вложение по 250000 руб. на обоих рынках.
3. Критерий Гурвица — критерий пессимизма-оптимизма. Параметр γ в нашем случае равен 0,4. Рассчитаем числа и выберем из них максимальное:
a1
= 0,4Ч(-18603,45) + 0,6Ч6757,18 = -3387,07
a2
= 0,4Ч (-21617,96) + 0,6Ч7344,87 = -4240,26
a3
= 0,4Ч5629,29 + 0,6Ч7430,39 = 6709,95
Таким образом при γ = 0,4, если руководство банка настроено оптимистично оно принимает решение вложить по 250000 руб. на обоих рынках.
4.Критерий Байеса — используется тогда, когда известны вероятности состояний природы. Такая ситуация называется ситуацией риска. Наилучшей, по Байесу, стратегией считается соответствующая наибольшему ожидаемому выигрышу. Рассчитаем а1
, а2
, а3
:
a1
= 0,4Ч (-18603,45) + 0,6Ч 6757,18 = -3387,07
a2
= 0,4Ч7344,87 + 0,6Ч (-21617,96) = -10032,82
a3
= 0,4Ч5629,29 + 0,6Ч7430,39 = 6709,95
Наилучшей, по Байесу, стратегией будет стратегия А3
.
Задание 7
Компания рассматривает строительство филиалов в четырех местах, соответственно имеются четыре проекта, продолжительностью 5 лет. Первоначальные инвестиции и доходы по годам приведены в таблице исходных данных. Инвестиционные возможности компании ограничены. В силу определенных соображений сумма расстояний от компании до филиалов не должна превышать 450 км. Из-за ограниченности фонда заработной платы общее число работников филиала на должно превышать 450 человек. Совместное строительство филиалов не допускается, так как они располагаются достаточно близко друг к другу.
Построить модель оптимального распределения инвестиций по проектам, в качестве критерия оптимальности использовать сумму NPV проектов. Ставка дисконта равна 15%.
| Номер проекта
|
I0
|
Доходы по годам
|
| первый
|
второй
|
третий
|
четвертый
|
пятый
|
| первый
|
1250
|
-200
|
600
|
1200
|
1300
|
1400
|
| второй
|
1300
|
100
|
830
|
700
|
570
|
720
|
| третий
|
1400
|
500
|
250
|
400
|
320
|
710
|
| четвертый
|
2200
|
-330
|
1000
|
1150
|
1600
|
1800
|
Решение
Для расчета NPV будем использовать следующую формулу:
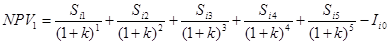 i = 1,2,3,4 i = 1,2,3,4
Отсюда:
NPV1
= 1258,12
NPV2
= 558,68
NPV3
= 22,78
NPV4
= 835,05
Введем переменные. Пусть хi
, i = 1,2,3,4 характеризует i-й проект и может принимать только 2 значения — 0 или 1. Если хi
= 0, это значит, что i-й проект не следует инвестировать. Если хi
= 1, то i-й проект следует инвестировать.
Используя введенные переменные запишем целевую функцию:
NPV = 1258,12х1
+ 558,68х2
+ 22,78х3
+ 835,05х4
Теперь запишем ограничения, которые вытекают из условий задачи.
Первое ограничение следует из ограниченности инвестиционных возможностей компании:
1250х1
+ 1300х2
+ 1400х3
+ 2200х4
≤5600
Второе ограничение следует из того, что в первом году некоторые проекты еще не требуют инвестиций, которые должны быть покрыты доходами от других проектов:
-200х1
+ 100х2
+ 500х3
- 300х4
≥0
Далее запишем ограничение, вытекающее из ограниченности суммы расстояний:
100х1
+ 90х2
+ 120х3
+ 160х4
≤450
Аналогично запишем ограничение, которое следует из того, что общее количество работников филиалов ограничено:
100х1
+ 120х2
+ 120х3
+ 150х4
≤450
Наконец, запишем условие того, что второй и третий филиалы одновременно строить нельзя:
х2
+ х3
≤1
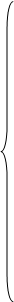 Модель оптимального распределения инвестиций по проектам состоит в максимизации целевой функции при ограничениях, т.е. Модель оптимального распределения инвестиций по проектам состоит в максимизации целевой функции при ограничениях, т.е.
NPV = 1258,12х1
+ 558,68х2
+ 22,78х3
+ 835,05х4
(max)
1250х1
+ 1300х2
+ 1400х3
+ 2200х4
≤5600
-200х1
+ 100х2
+ 500х3
- 300х4
≥0
100х1
+ 90х2
+ 120х3
+ 160х4
≤450
100х1
+ 120х2
+ 120х3
+ 150х4
≤450
х2
+ х3
≤1
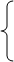 0, если i-й проект не инвестировать 0, если i-й проект не инвестировать
xi
=
1, если i-й проект инвестировать, i=1,2,3,4
|