КУРСОВАЯ РАБОТА
по дисциплине
Статистика
на тему:
«Применение статистических методов в экономических исследованиях»
Ставрополь 2009
Содержание
Введение ………………………………………………………………………….3
1. Система показателей статистики банков…………………………………5
2. Статистический анализ изменения цен производителей в регионе…...10
3. Расчетно-аналитическая часть…………………………………………...18
Заключение……………………………………………………………………….35
Список литературы………………………………………………………………36
Введение
Произошедшие в последнее время в России коренные изменения в общественно-экономической и социальной жизни общества, переход на рыночные отношения вызвали потребность в значительном совершенствовании социально-экономической статистики и общей теории статистики. В частности, в комплексном пересмотре всей системы учета и статистики в стране, необходимость расширения возможности получения точной, объективной и аналитической информации о состоянии и развитии социально-экономических процессов для принятия решения на всех уровнях управления.
Статистическое наблюдение представляет собой массовое, планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, заключающееся в регистрации отобранных признаков у каждой единицы совокупности.
Экономическая статистика разрабатывает и анализирует синтетические показатели, отражающие состояние национальной экономики; структуру, пропорции, взаимосвязь отраслей и элементов общественного воспроизводства; рассматривает особенности размещения производительных сил, состав и использование, материальных, трудовых и финансовых ресурсов; наконец, осуществляет построение и анализ общей макростатистической модели рыночной экономики в виде системы национальных счетов (СНС).
Отрасли экономической статистики – статистика промышленности, сельского хозяйства, строительства, транспорта, связи, труда, природных ресурсов, охраны окружающей среды и т.д. – разрабатывают и изучают статистические показатели развития соответствующих отраслей.
Социально-демографическая статистика формирует и анализирует систему показателей, комплексно характеризующих различные стороны социальных условий и образа жизни населения; ее отрасли – статистика населения, политики, культуры, здравоохранения, науки, просвещения, права и т.д.
Задачей всех отраслевых статистик является разработка статистических показателей соответствующих отраслей.
Статистика развивается как единая наука, и развитие каждой отрасли содействует ее совершенствованию в целом.
Между наукой-статистикой и практикой существует тесная взаимосвязь: статистика использует данные практики, обобщает и разрабатывает методы проведения статистических исследований. В свою очередь, в практической деятельности применяются теоретические положения статистической науки для решения конкретных управленческих задач.
Знание статистики необходимо современному специалисту для принятия решений в условиях стохастики (когда анализируемые явления подвержены влиянию случайностей), для анализа элементов рыночной экономики, в сборе информации, в связи с увеличением хозяйственных единиц и их типов, аудите, финансовом менеджменте, прогнозировании.
Раздел 1. Система показателей статистики банков
Предметом изучения статистики банков является количественная характеристика массовых явлений в сфере денежного обращения и кредитных отношений.
Денежное обращение- это движение денег во внутреннем обороте в наличной и безналичной формах в процессе обращения товаров, оказания услуг и совершения различных платежей. Денежное обращение охватывает движение не только товаров и услуг, но и ссудного и фиктивного капитала. Значительная часть платёжного оборота в странах с рыночной экономикой приходится на финансовые операции, т.е. на сделки с различными видами ценных бумаг, ссудные операции, налоговые платежи и прочие финансовые сделки, большая часть денежного оборота осуществляется в безналичной форме, что связано с резким увеличением платежно-расчетных операций.
Система статистических показателей, характеризующих денежное обращение, основывается на категориях, связанных с функциями денег, определениями денежной массы и её структуры.
Система показателей денежного обращения включает следующие показатели:
-денежная масса и её структура;
-обеспеченность денежными знаками обращения национальной экономики и покупательная способность денежной единицы (национальной валюты);
-показатели, отражающие операции на счетах, с депозитами, золотым запасом государства;
-показатели, отражающие операции с валютой в международных экономических отношениях. В процессе обращения товаров, оказания услуг и совершения различных платежей осуществляется движение денег во внутреннем обороте в наличной и безличной формах. Всю денежную массу можно представить как совокупный денежный агрегат (М3
), включающий в качестве составных частей денежные агрегаты М0
, М1
, М2
. При построении этих агрегатов каждая последующая величина возрастает на предыдущую.
М3
-денежная масса в обороте, измеряемая совокупным объёмом покупательных и платёжных средств, обслуживающих хозяйственный оборот и принадлежащих частным лицам, предприятиям и государству (кроме центрального правительства).
В состав совокупной денежной массы, рассчитываемой Банком России, входят следующие показатели:
1. Денежный агрегат М0
– наличные деньги в обращении, т.е. не включая наличные деньги, держателем которых является банковская система.
2. Средства на расчётных, текущих и специальных счетах предприятий, населения и местных бюджетов.
3. Депозиты населения и предприятий в коммерческих банках.
4. Депозиты населения до востребования в сберегательных банках.
5. Средства Госстраха.
Денежный агрегат М1
= (М0
+ п.2 + п.3 + п.4 + п.5).
6. Срочные депозиты населения в сберегательных банках.
Денежный агрегат М2
= (М1 + п.6).
7. Сертификаты и облигации госзайма.
Денежный агрегат М3
= (М2
+ п.7).
Самостоятельным компонентом денежной массы является показатель денежной базы. Денежная база включает денежный агрегат М0
(наличные деньги в обращении), денежные средства в кассах банков, обязательные резервы коммерческих банков в Центральном банке и их средства на корреспондентских счетах в Центральном банке. Для контроля за динамикой денежной массы, анализа возможности коммерческих банков расширить объёмы кредитных вложений в экономику используется показатель «денежный мультипликатор».
Денежный мультипликатор – это коэффициент, характеризующий увеличение денежной массы в обороте в результате роста банковских резервов. Он рассчитывается по формуле:
М2
/Н = (С+D) / (C+R) = (C/D +1) / (C/D + R/D),
где М2
– денежная масса в обращении;
H – денежная база;
С – наличные деньги;
D – депозиты;
R- обязательные резервы коммерческих банков.
Предельная (максимально возможная) величина денежного мультипликатора находится в обратной зависимости к ставке обязательных резервов, устанавливаемой Центральным банком для коммерческих банков.
Соответствие количества денежных знаков объёму обращения и факторы обесценения денег определяются с помощью следующих показателей:
1. количество денежных единиц, необходимых в данный период для обращения;
2. показатель, характеризующий, во сколько раз произведение количества денег на скорость обращения больше произведения уровня цен на товарную массу;
3. показатель инфляции.
В соответствии с экономическим законом денежного обращения в каждый данный период количество денежных единиц, необходимых для обращения, определяется по формуле:
Д = (Ц – В + П – ВП)/С0
где Ц – сумма цен товаров, подлежащих реализации;
В – сумма цен товаров, платежи по которым выходят за рамки данного периода;
П – сумма цен товаров, проданных в прошлые периоды, сроки платежей по которым наступили;
ВП – сумма взаимопогашаемых платежей;
С0
– скорость оборота денежной единицы (сколько раз в году оборачивается рубль).
В упрощённом виде эта формула выглядит так:
Д = (М Цср
)/ С0
где М – масса реализуемых товаров;
Цср
– средняя цена товара.
Из вышеприведённой формулы получаем равенство (уравнение обмена):
ДС0
= М Цср
.
Следовательно, произведение количества денег в обращении на скорость обращения (ДС0
) равно произведению товарной массы на уровень цен (М Цср
). Когда равенство нарушается (ДС0
> М Цср
) происходит обесценение денег. Указанное уравнение обмена впервые предложено И.Фишером. Современный монетаризм (М.Фридман и др.) также основывается на уравнении И.Фишера. Но если И.Фишер делает упор на взаимосвязи денежного феномена с ценами, то М.Фридман увязывает динамику денежного фактора с номинальным ВВП.
Обесценение денег, проявляющееся в форме роста цен на товары и услуги (инфляция), возникает вследствие переполнения каналов денежного обращения избыточной денежной массы при отсутствии адекватного увеличения товарной массы. Инфляция, как правило, измеряется с помощью двух индексов-дефляторов: дефлятора ВВП и индекса потребительских цен. Чаще всего измерения инфляции применяется индекс потребительских цен. К важным показателям статистики денежного обращения относится показатель, характеризующий изменение покупательной способности рубля (Iп.с.р.
), который определяется как обратная величина индекса потребительских цен (Iп.ц.
). В самом общем виде этот показатель можно определить по формуле:
1 1 ∑ P0
Q1
Iп.с.р.
= -------- = ----------------------- = -------------- ,
Iп.ц.
∑ P1
Q1
/ ∑ P0
Q1
∑ P1
Q1
где Q1
– объём товаров и услуг, потребляемых населением и включаемых в их денежные расходы в текущем периоде;
P0
и P1
– цены на товары и услуги, потребляемые населением соответственно в базисном и текущем периоде.
Раздел 2. Статистический анализ изменения цен производителей в регионе
Цены - сложная система, составной элемент рыночного механизма. Следовательно, статистическое изучение цен требует развернутой системы показателей, соответствующей требованиям рыночной экономики. Система показателей должна отразить различные виды дифференциации рыночных цен: ассортиментный, территориальный, во времени, по социально-доходным группам, раз личным субрынкам.
Таблица 2. Система показателей статистики цен
Блоки
показателей
|
Показатели |
Субпоказатели |
| Уровень цен |
Индивидуальный уровень |
Моментная цена товарного вида, сорта товара-представителя |
| Средний уровень |
Средняя цена на дату и за период: по товарной группе ( комплексу ); по территории, в том числе городу и селу; по субрынкам; по группам покупателей |
| Обобщающий уровень |
Стоимость потребительской корзины; отношение индивидуальной, средней и обобщающей цены к доходу |
| Структура цены |
Себестоимость, наценки, скидки (оптовые, розничные), налоги |
Удельный вес каждого элемента в конечной (розничной) цене товара; удельный вес валового дохода (реализованного наложения) в товарообороте; соотношение оптовых и розничных цен; соотношение структурных элементов розничных цен |
| Соотношение цен |
Коэффициенты соотношения цен регионов, субрынков, товаров |
Отношение цен товаров к базовой цене; степень отклонения соотношений цен от базовых; степень устойчивости соотношений в динамике |
| Вариация цен |
Показатели вариации цен в пространстве (социально-экономическом и географическом) и во времени |
Распределение цен в пределах товарной группы (группировка одноименных товаров по уровню цен); уровень территориальной колеблимости цен; уровень устойчивости цен в динамике (коэффициент аппроксимации трендовой модели); уровень сезонных и циклических колебаний цен; степень различий цен покупок в социальных группах населения (группировки потребителей по уровню цен покупки) |
| Динамика цен |
Показатели динамики отдельных товаров-представителей, товарных групп, всех товаров
|
Индивидуальные индексы цен; групповые индексы цен; общий (сводный) индекс цен; индекс средних цен; тренд цен |
Соответствие цены качеству товара и покупательским мнениям
|
Показатели влияния качества на цену, динамику качества, динамику цен
|
Параметры моделей; коэффициенты эластичности; индексы; экспертные оценки
|
| Эластичность |
Показатели зависимости цен от социально-экономических факторов, зависимости цен одних товаров от цен других |
Эмпирический коэффициент эластичности; коэффициент перекрестной эластичности; теоритический коэффициент эластичности |
Рынок делает цены гибкими, чутко реагирующими на изменение различных факторов. Поэтому показатели эластичности цен, их соотношений должны найти отражение в системе показателей статистики цен. Возможность для населения выбора товаров с определенным сочетанием качества и цен, соответствующих определенному уровню дохода и потребительским требованиям, определяет необходимость использования в системе показателей статистических оценок соответствия и отражения в цене качества товара, потребительских предпочтений.
Важнейшими остаются показатели динамики (особенно индексы) и прогнозные оценки (с учетом прогноза условий и факторов, влияющих на цены). Особое значение приобретают показатели динамики цен, учитывающие качественные изменения товаров. Система показателей статистики цен отражает диалектическое единство анализа цен в статике и динамике, сочетание синтетического и аналитического подхода к изучению указанных проблем, включает показатели государственной статистики цен и статистики цен рыночных структур.
Ведущая роль в статистическом изучении динамики цен принадлежит индексному методу. Сравнение цен одного товара осуществляется с помощью индивидуального (однотоварного) индекса цен:
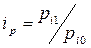
где pi0 , pi1 – цены на товар в базисном и текущем периоде.
Индекс средних цен применяется при изучении изменения цен товарных групп, цен одного товара по различным территориям и субрынкам:

где pi1, qi1 - цена и количество проданного i - го вида товара (товара на i - й территории или i - м субрынке) в отчетном году, i=l,…, n;
pi1, qi1 - цена и количество проданного i - го вида товара (товара на i - й территории или i - м субрынке) в базисном году, i=l,…, n.
Товары должны быть достаточно однородными, чтобы их количество поддавалось суммированию.
Основной формой индекса цен для совокупности разнородных товаров является агрегатный индекс. Цены различных товаров (например, кондитерских изделий и компьютеров) складывать бессмысленно. Несуммируемость элементов совокупности преодолевается путем взвешивания каждой цены по количеству проданных товаров. Сумма произведений цен товаров на их количество составляет товарооборот совокупности товаров. Чтобы выявить непосредственно изменение цен, необходимо зафиксировать показатели количества на одном из уровней:
– базисного периода времени (формула Ласпейреса);

– текущего периода времени (формула Пааше)
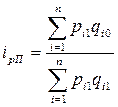
Четкость интерпретации, экономический смысл и удобство практического расчета формулы Ласпейреса сделали ее самой популярной в мире для расчета индекса потребительских цен, который показывает, во сколько раз изменились бы потребительские расходы в текущем периоде по сравнению с базисным, если бы при изменении цен уровень потребления оставался прежним. Такой расчет корректен при отсутствии значительных количественных и качественных изменений в структуре потребления (во времени и по территории, если индекс рассчитывается для нескольких регионов).
Доказано, что наилучший линейный индекс лежит между индексами, вычисленными по формулам Ласпейреса и Пааше. Зарубежные статистики пытались найти компромиссную формулу.
Формула Эджворта - Маршалла:
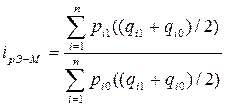
Формула улавливает сдвиги в структуре покупок, но привязана к условной структуре товарооборота, не характерной ни для одного реального периода, не имеет прямого экономического смысла. Ее расчет встречает препятствия в сборе материалов.
Наиболее удачным компромиссом многие экономисты считают «идеальный» индекс Фишера:
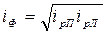
который оценивает не только набор товаров базисного периода по ценам текущего, но и набор товаров текущего периода по ценам базисного. Применяется в случае трудностей с выбором весов или значительного изменения структуры весов.
Разновидностью розничных цен являются цены на продукты массового (общественного) питания. Они образуются на базе розничных или оптовых цен на продукты, покупаемые предприятиями массового питания с добавлением наценки, возмещающей издержки на переработку продуктов и дающей прибыль. Непосредственная регистрация цен продукции массового питания практически невозможна из-за большого разнообразия ее состава и отсутствия стабильной единицы измерения. Поэтому для расчета индекса цен на продукцию массового питания исчисляют индекс цен на израсходованные продукты и товары, проданные на предприятиях массового питания, и индекс ценовых факторов наценки (Inp). Последний, в свою очередь, состоит из двух индексов: индекса норм наценок (т. е. процента наценки к цене продукта) и индекса изменения самих цен:
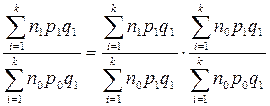
где n1, p1, q1 – норма наценки, цена и количество товаров в отчетном году, n0, p0, q0 – норма наценки, цена и количество товаров в базисном году; k – число i-x разновидностей товаров;
Так как расход продуктов в производстве продукции массового питания учитывается в стоимостных единицах, то для расчета используется формула среднего гармонического индекса:

где inp
= in
* ip
= n1
p1
/ n0
p0
Формула индекса цен массового питания имеет вид:

Индексы при систематическом расчете из года в год образуют индексные ряды. Различают базисные ряды (цены каждого года сравниваются с ценами года, принятого за базу) и цепные (характеризующие изменение цен по сравнению с предыдущим годом). Веса индексов ряда могут быть постоянными (на уровне одного года), и тогда произведение цепных индексов даст базисный индекс.
Применение системы переменных весов (по количеству товаров отчетного года) в индексном ряду цен порождает ошибку при переходе от цепных индексов к базисным и обратно, так как позитивна корреляция между текущим изменением цен и прошлым изменением количества проданных товаров. Эта ошибка мала, если корреляционная связь между изменением цен и количества проданного товара незначительна. На практике система цепных индексов (достоинство - сокращает период сравнения, ограничивает круг несопоставимых товаров) используется для коротких периодов, затем осуществляется поправка по формуле базисного периода, так как за длительный период ошибка накапливается.
Большой интерес для статистического анализа представляют данные о средних ценах в Карачаево-Черкесской Республике. В табл. 2 представлены данные о средних ценах на некоторые продовольственные товары.
Таблица 2. – Средние потребительские цены на отдельные продовольственные товары.
рублей за килограмм
| 2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
Говядина (кроме
бескостного мяса)
|
43,22
|
61,56
|
66,50
|
64,57
|
78,04
|
101,05
|
111,09
|
113,56
|
Свинина (кроме
бескостного мяса)
|
59,01
|
84,43
|
85,64
|
78,86
|
124,64
|
151,45
|
143,62
|
155,90
|
Баранина (кроме
бескостного мяса)
|
58,04
|
76,86
|
84,30
|
80,50
|
98,82
|
127,26
|
133,17
|
143,62
|
| Куры (кроме куриных окорочков) |
48,94
|
60,33
|
66,72
|
74,34
|
74,79
|
80,36
|
78,88
|
94,94
|
| Колбаса полукопченая |
63,23 |
81,49 |
85,57 |
84,79 |
103,57 |
119,37 |
131,60 |
153,40 |
| Рыба замороженая неразделанная |
25,81
|
31,25
|
30,60
|
31,59
|
34,48
|
42,31
|
42,07
|
48,46
|
| Масло сливочное |
60,64 |
63,30 |
72,71 |
74,54 |
78,16 |
84,97 |
91,18 |
132,54 |
| Масло подсолнечное |
20,98 |
29,27 |
33,58 |
34,58 |
36,49 |
36,40 |
36,69 |
56,58 |
Молоко цельное
разливное непастеризованное, за литр
|
6,43
|
8,77
|
9,57
|
9,38
|
11,64
|
12,84
|
14,62
|
20,54
|
Сыры сычужные
твердые и мягкие
|
72,06
|
87,75
|
93,00
|
99,90
|
107,32
|
125,60
|
127,95
|
215,33
|
| Яйца куриные, за 10 шт |
16,90 |
18,33 |
22,10 |
22,76 |
28,69 |
27,22 |
30,10 |
36,06 |
| Сахар – песок |
14,28 |
13,55 |
17,60 |
17,22 |
18,56 |
19,03 |
22,22 |
20,38 |
| Мука пшеничная |
7,08 |
6,86 |
6,67 |
9,56 |
11,38 |
9,77 |
11,17 |
15,48 |
| Хлеб пшеничный из муки 1 и 2 с. |
7,52
|
8,01
|
8,22
|
13,29
|
13,13
|
12,99
|
13,68
|
18,60
|
| Рис шлифованный |
11,49 |
11,88 |
15,49 |
15,20 |
19,57 |
19,26 |
21,98 |
28,92 |
Макаронные изделия
из пшеничной муки
высшего сорта
|
13,66
|
14,86
|
16,18
|
16,49
|
22,06
|
21,71
|
22,05
|
29,70
|
| Картофель |
4,53 |
4,88 |
9,17 |
8,02 |
7,08 |
8,02 |
11,61 |
13,24 |
| Капуста белокочанная свежая |
3,48
|
3,65
|
10,94
|
4,36
|
5,36
|
8,53
|
7,92
|
17,72
|
| Лук репчатый |
3,35 |
6,06 |
11,71 |
9,09 |
7,53 |
9,41 |
12,51 |
15,34 |
| Яблоки |
13,05 |
17,22 |
19,26 |
17,00 |
21,55 |
24,98 |
38,81 |
38,99 |
| Водка обыкновенного качества, за литр |
74,69
|
80,02
|
89,03
|
95,02
|
119,85
|
131,81
|
153,76
|
173,74
|
Средние цены являются показателями, на основе которых вычисляют индексы цен, показывающие изменение цены. Рассмотрим динамику индексов цен по секторам экономики (табл. 3).
Таблица 3. – Динамика индексов цен по секторам экономики в КЧР
| 2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
| Индекс потребительских цен |
113,4 |
119,2 |
119,2 |
109,4 |
112,1 |
112,4 |
110,3 |
114,9 |
Индекс цен производителей
промышленных товаров
|
129,3
|
112,6
|
112,7
|
111,3
|
112,7
|
132,0
|
117,2
|
122,3 |
Индекс цен производителей
на реализованную сельскохозяйственную продукцию |
114,6
|
104,9
|
93,9
|
120,8
|
92,5
|
161,6
|
90,5
|
81,7
|
| Сводный индекс цен строительной продукции |
144,5
|
109,7
|
109,9
|
106,9
|
108,2
|
118,1
|
107,1
|
110,2 |
Индекс тарифов на грузовые
перевозки автомобильным транспортом |
121,2
|
123,4
|
105,4
|
100,0
|
159,4
|
131,3
|
112,1
|
107,4 |
Индекс тарифов на услуги
связи для юридических лиц |
107,9
|
115,7
|
107,6
|
109,4
|
106,7
|
105,0
|
106,2
|
103,4 |
| Индекс цен на вторичном рынке жилья |
97,5
|
106,8
|
115,0
|
118,5
|
218,2
|
111,6
|
101,9
|
120,7
|
Раздел 3.Расчетно-аналитечская часть.
Задача 1.
1. С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском продукции произведите группировку предприятий по среднегодовой стоимости основных производственных фондов, образовав пять групп предприятий с равными интервалами. По каждой группе и совокупности предприятий подсчитайте:
а) число предприятий и их структуру по группам в процентах к итогу;
б) среднегодовую стоимость основных производственных фондов - всего и в среднем на один завод;
в) стоимость продукции - всего и в среднем на один завод.
2. Результаты группировки проиллюстрируйте графически, для чего постройте:
а) гистограмму распределения;
б) секторную диаграмму (по структуре заводов по группам).
3. По данным группировки изучить тесноту связи между выпуском продукции на одно предприятие (результативный признак - у
) и оснащенностью предприятий основными производственными фондами (факторный признак - х
), вычислив коэффициент детерминации и эмпирическое корреляционное отношение. Пояснить их значение.
Таблица 4 - Исходные данные
| Номер предприятия |
Среднегодовая стоимость основных производственных фондов, млн. руб. |
Объем продукции в сопоставимых ценах,
млн. руб.
|
| 1 |
170 |
270 |
| 2 |
120 |
204 |
| 3 |
130 |
135 |
| 4 |
177 |
172 |
| 5 |
48 |
58 |
| 6 |
96 |
77 |
| 7 |
77 |
126 |
| 8 |
178 |
170 |
| 9 |
55 |
66 |
| 10 |
76 |
87 |
| 11 |
98 |
197 |
| 12 |
174 |
175 |
| 13 |
37 |
77 |
| 14 |
199 |
300 |
| 15 |
204 |
210 |
| 16 |
375 |
570 |
| 17 |
126 |
178 |
| 18 |
179 |
201 |
| 19 |
794 |
750 |
| 20 |
251 |
320 |
| 21 |
764 |
785 |
| 22 |
75 |
174 |
| 23 |
66 |
89 |
| 24 |
704 |
75 |
| 25 |
70 |
40 |
Решение.
Зная число групп, определим величину интервала по формуле:
i = (
xmax
-
xmin
) /
n =
(794-37)/5 =151,4
Таблица 5. Группировка предприятий.
| № группы |
Группировка предприятий
по среднегодовой стоимости
|
№ предприятия |
Среднегодовая стоимость
основных фондов
|
Объем продукции в сопоставимых ценах, млн. руб. |
Фондоотдача, в руб. на 1000 руб. ОФ |
| 1 |
37-188,4 |
13 |
37 |
77 |
2081,1 |
| 5 |
48 |
58 |
1208,3 |
| 9 |
55 |
66 |
1200,0 |
| 23 |
66 |
89 |
1348,5 |
| 25 |
70 |
40 |
571,4 |
| 22 |
75 |
174 |
2320,0 |
| 10 |
76 |
87 |
1144,7 |
| 7 |
77 |
126 |
1636,4 |
| 6 |
96 |
77 |
802,1 |
| 11 |
98 |
197 |
2010,2 |
| 2 |
120 |
204 |
1700,0 |
| 17 |
126 |
178 |
1412,7 |
| 3 |
130 |
135 |
1038,5 |
| 1 |
170 |
270 |
1588,2 |
| 12 |
174 |
175 |
1005,7 |
| 4 |
177 |
172 |
971,8 |
| 8 |
178 |
170 |
955,1 |
| 18 |
179 |
201 |
1122,9 |
| Итого по группе:
|
18
|
1952
|
2496
|
1278,7
|
| 2 |
188,4-339,8 |
14 |
199 |
300 |
1507,5 |
| 15 |
204 |
210 |
1029,4 |
| 20 |
251 |
320 |
1274,9 |
| Итого по группе:
|
3
|
654
|
830
|
1269,1
|
| 3 |
339,8-491,2 |
16 |
375 |
570 |
1520,0 |
| Итого по группе:
|
1
|
375
|
570
|
1520,0
|
| 4 |
491,2-642,6 |
0 |
0 |
0 |
0,0 |
| Итого по группе:
|
0
|
0
|
0
|
0,0
|
| 5 |
642,6-794 |
24 |
704 |
75 |
106,5 |
| 21 |
764 |
785 |
1027,5 |
| 19 |
794 |
750 |
944,6 |
| Итого по группе:
|
3
|
2262
|
1610
|
711,8
|
В результате получаем пять групп. При чем, в четвертой группе у нас нету ни одного предприятия
На основе полученной группировки построим диаграмму и графически покажем распределение предприятий.

Рис.1. Структура предприятий по группам

Рис.2. Распределение предприятий по группам.
Используя результаты, полученные в первой таблицы, построим еще одну таблицу.
Таблица 6. Разработочная таблица.
| № группы |
Группировка предприятий |
Кол-во предп. |
Среднегодовая стоимость ОФ |
Выпуск продукции |
Фондоотдача, в руб. на тыс.руб.ОФ |
| по среднегодовой стоимости |
всего |
в среднем на 1 предприятие |
всего |
в среднем на 1 предприятие |
| 1 |
37-188,4 |
18 |
1952 |
108,4 |
2496 |
138,7 |
1278,7 |
| 2 |
188,4-339,8 |
3 |
654 |
218,0 |
830 |
276,7 |
1269,1 |
| 3 |
339-8-491,2 |
1 |
375 |
375,0 |
570 |
570,0 |
1520 |
| 4 |
491,2-642,6 |
0 |
0 |
0,0 |
0 |
0,0 |
0 |
| 5 |
642,6-794 |
3 |
2262 |
754,0 |
1610 |
536,7 |
711,8 |
| Итого |
25 |
5243 |
209,7 |
5506 |
220,2 |
1050,2 |
Чтобы исчислить коэффициент детерминации и эмпирическое корреляционное отношение необходимо найти общую и межгрупповую дисперсии.
Для расчета дисперсий исчислим средний выпуск продукции по каждой группе и общий средний выпуск продукции:
-по первой группе  =2496/18=138,7 =2496/18=138,7
- по второй группе  = 830/3=276,7 = 830/3=276,7
- по третьей группе  =570/1=570 =570/1=570
- по четвертой группе  = 0 = 0
- по пятой группе  = 1610/3=536,7 = 1610/3=536,7
Общий средний выпуск продукции по всем группам: 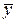 = 5506/25=220,2 = 5506/25=220,2
Строим вспомогательную расчетную таблицу.
Таблица 7. Вспомогательная таблица
| № группы |
№ предприятия |
Объем продукции в сопоставимых ценах, |
 |
 |
 |
 |
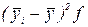 |
1
|
13 |
77 |
-143,2 |
20506,2 |
-81,5 |
6642,3 |
119560,5 |
| 5 |
58 |
-162,2 |
26308,8 |
| 9 |
66 |
-154,2 |
23777,6 |
| 23 |
89 |
-131,2 |
17213,4 |
| 25 |
40 |
-180,2 |
32472,0 |
| 22 |
174 |
-46,2 |
2134,4 |
| 10 |
87 |
-133,2 |
17742,2 |
| 7 |
126 |
-94,2 |
8873,6 |
| 6 |
77 |
-143,2 |
20506,2 |
| 11 |
197 |
-23,2 |
538,2 |
| 2 |
204 |
-16,2 |
262,4 |
| 17 |
178 |
-42,2 |
1780,8 |
| 3 |
135 |
-85,2 |
7259,0 |
| 1 |
270 |
49,8 |
2480,0 |
| 12 |
175 |
-45,2 |
2043,0 |
| 4 |
172 |
-48,2 |
2323,2 |
| 8 |
170 |
-50,2 |
2520,0 |
| 18 |
201 |
-19,2 |
368,6 |
| Итого |
18
|
2496
|
-1467,6 |
189110,3 |
-81,5 |
6642,25 |
119560,5 |
2
|
14 |
300 |
79,8 |
6368,0 |
56,5 |
3192,3 |
9576,75 |
| 15 |
210 |
-10,2 |
104,0 |
| 20 |
320 |
99,8 |
9960,0 |
| итого |
3
|
830
|
169,4 |
16432,12 |
56,5 |
3192,3 |
9576,75 |
| 3 |
16 |
570 |
349,8 |
122360,0 |
349,8 |
122360,0 |
122360 |
| итого |
1
|
570
|
349,8 |
122360 |
349,8 |
122360 |
122360 |
| 4 |
0
|
0
|
0 |
0 |
0 |
0 |
0 |
5
|
24 |
75 |
-145,2 |
21083,0 |
316,5 |
100172,3 |
300516,8 |
| 21 |
785 |
564,8 |
318999,0 |
| 19 |
750 |
529,8 |
280688,0 |
| Итого |
3
|
1610
|
949,4 |
620770,1 |
316,5 |
100172,3 |
300516,8 |
| Всего |
25 |
5506 |
1 |
948672,6 |
641,3 |
232366,8 |
552014,1 |
Исчислим межгрупповую дисперсию по формуле
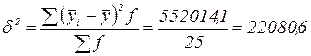
Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп предприятий по среднегодовой стоимости ОПФ.
Исчислим общую дисперсию по формуле:
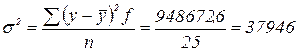
Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию выпуска продукции всеми предприятиями.
Исчислим эмпирический коэффициент детерминации:
 (или 58,19 %) (или 58,19 %)
Это означает, что на 58,19% вариация выпуска продукции предприятиями обусловлена различиями в среднегодовой стоимости их основных фондов и на 41,81 % -влияние прочих факторов.
Найдем эмпирическое корреляционное отношение:
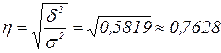
Эмпирическое корреляционное отношение показывает тесноту связи между среднегодовой стоимостью ОФ и выпуском продукции. Сила свзяи равняется 0,76, что свидетельствует о тесной связи между среднегодовой стоимостью ОФ и выпуском продукции.
Задача 2.
В целях изучения норм расхода сырья на единицу продукции из партии изделий проведена 10 %-ная механическая выборка (бесповторная), в результате которой получено распределение:
Таблица 8 - Исходные данные
| Расход сырья, г |
Изготовлено изделий, шт. |
| До 20 |
8 |
| 20-28 |
17 |
| 28-36 |
50 |
| 36-44 |
27 |
| Свыше 44 |
7 |
| Итого |
109 |
Определить:
1. Средний расход сырья на одно изделие.
2. Дисперсию и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0,954 - возможные пределы расхода сырья на единицу продукции для всей партии изделий.
6. С вероятностью 0,997 - возможные пределы доли (удельного веса) изделий с расходом сырья от 20 до 36 г.
Решение:
1. Средний расход сырья на одно изделие находим по формуле средней арифметической взвешенной (х- середина интервала; f- частота, т.е. число изделий в каждой группе):

Таблица 9.
| Группы изделий по удельному расходу сырья, г |
Количество изделий, шт. f |
Середина интервала
х
|
Х*f
|
Накопленная частота,
S
|
Х2
*f
|
(х- )2
*f )2
*f
|
| до 20 |
8 |
16 |
128 |
8 |
2048 |
2204,5 |
| 20-28 |
17 |
24 |
408 |
25 |
9792 |
1257,3 |
| 28-36 |
50 |
32 |
1600 |
75 |
51200 |
18,0 |
| 36-44 |
27 |
40 |
1080 |
102 |
43200 |
1478,5 |
| Свыше 44 |
7 |
48 |
336 |
109 |
16128 |
1660,1 |
| Итого:
|
109 |
-
|
3552
|
--
|
122368 |
6618,4 |
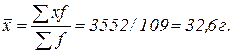 , т.е. в среднем удельный расход сырья составляет 32,6 г. , т.е. в среднем удельный расход сырья составляет 32,6 г.
2. Для нахождения среднего квадратичного отклонения используем формулу:
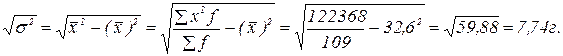
Дисперсию рассчитываем по формуле:

3. Коэффициент вариации является показателем однородности ряда и рассчитывается как отношение среднего квадратического отклонения к среднему значению выполнения норм выработки:
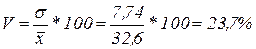
Так как коэффициент вариации меньше 33%, то данную совокупность можно считать однородной.
4. Так как выборка бесповторная 10 %- ная, то формула нахождения предельной ошибки выборочной средней будет:
 г. г.
При этом коэффициент Лапласа t
определяется в зависимости от значения вероятности. В данном случае вероятность равна 0,954, следовательно, коэффициент Лапласа будет равен 2.
Тогда границы генеральной средней будут равны:
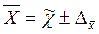 , ,


Это означает, что в генеральной совокупности значение среднего удельного расхода сырья будет находиться в интервале от 31,2 г. до 34г.
5. Долю изделий с удельным расходом сырья от 20 до 36 г. во всей партии продукции по выборочной совокупности можно найти как сумму вариант соответствующих интервалов, т.е. искомая доля составит:
w = m / n =
67/109 = 0,61 или 61% из всей выборочной совокупности.
При этом m
– число изделий с удельным расходом от 20 до 36 г. на одно изделие, n
– численность всех изделий, попавших в выборочное обследование.
Так как вероятность по условию равна 0,997, то коэффициент t
будет равен 3.
Предельная ошибка выборочной доли для бесповторного отбора находится по следующей формуле:
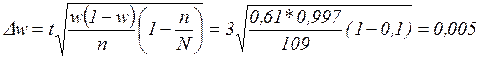 или 0,5% или 0,5%
Тогда границы генеральной доли будут следующими:
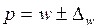


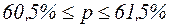
Т.е. доля изделий с удельным расходом сырья от 20 до 36г. и выше по генеральной совокупности будет колебаться от 60,5% до 61,5%.
Задача 3
На основании имеющихся данных вычислите:
1. Для рынка 1 (по двум видам товаров вместе):
а) общий индекс товарооборота;
б) общий индекс цен;
в) общий индекс физического объема продаж.
Определите в отчетном периоде изменение объема товарооборота и разложите по факторам (за счет изменений цен и объема продаж).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух рынков вместе (по продукции МП-25);
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры продаж товаров на динамику средней цены.
Объясните разницу между величинами индексов постоянного и переменного состава.
Таблица 10. Исходные данные
| Вид товара |
Продано товаров, тыс. единиц |
Цена единицы товара, тыс. руб. |
| базисный период |
отчетный период |
базисный период |
Отчетный период |
Рынок 1
МП-25
МП-29
Рынок 2
МП-25
|
175
377
176
|
179
370
174
|
75,0
77,0
7,0
|
74,1
78,2
6,6
|
Решение:
1. Для рынка 1 по двум видам товаров.
Чтобы вычислить для рынка 1 общий индекс товарооборота, общий индекс цен, общий индекс физического объема продаж составим таблицу.
Таблица 11.
Вид товара
|
Продано товаров, тыс. единиц |
Цена единицы товара, тыс. руб. |
| базисный период |
отчетный период |
базисный период |
Отчетный период |
| g0
|
g1
|
p0
|
p1
|
g0
p0
|
g1
p1
|
g1
p0
|
g0
p1
|
| Рынок 1 |
| МП-25 |
175 |
179 |
75 |
74,1 |
13125 |
13264 |
13425 |
12968 |
| МП-29 |
377 |
370 |
77 |
78,2 |
29029 |
28934 |
28490 |
29481 |
| Итого: |
552 |
549 |
152 |
152,3 |
42154 |
42198 |
41915 |
42449 |
| Рынок 2 |
| МП-25 |
176 |
174 |
7 |
6,6 |
1232 |
1148 |
1218 |
1162 |
| Итого по продукции МП-25 |
351 |
353 |
82 |
80,7 |
14357 |
14412,3 |
14643 |
14129 |
| Итого по 2 рынкам |
728 |
723 |
159 |
159 |
43386 |
43346 |
43133 |
43611 |
а) общий индекс товарооборота:
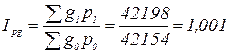
За счет всех факторов общий товарооборот увеличился на 0,1%, то есть на 44 тыс.руб.
б) общий индекс цен:
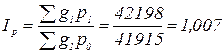
За счет изменения цен, общий товарооборот увеличился на 0,7 %, т.е. на 283 тыс.руб.
в) общий индекс физического объема продаж:
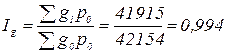
За счет изменения объема продаж общий товарооборот уменьшился на 0,6% или 239 тыс.руб.
Взаимосвязь индексов выглядит следующим образом:
Ipg
=Ip
Ig
= 1,007*0,994=1,001
2. Для двух рынков вместе по продукции МП-25.
а) Индекс цены переменного состава вычисляем по формуле:

За счет изменения всех факторов цена уменьшилась на 0,2%.
б) Индекс цен постоянного (фиксированного) состава или индекс цен в постоянной структуре:

За счет изменения структуры цены средняя цена уменьшилась на 1,6%
в) Индекс структурных сдвигов:

Индекс структурных сдвигов можно также определить, используя взаимосвязи индексов:
 = 0,998/0,984= 1,014
= 0,998/0,984= 1,014
За счет изменения структуры продаж средняя цена увеличилась на 1,4 %.
Задача 4
На основании данных об изменении численности населения города за год (тыс. чел.), определить:
а) численность постоянного и наличного населения на начало и на конец года;
б) коэффициенты рождаемости, смертности и естественного прироста населения;
в) механический прирост постоянного населения города за год и коэффициент механического прироста населения.
Таблица 12. Исходные данные
Данные об изменении численности населения города за год,
тыс. чел.
|
На начало года:
Фактически проживало 370
из них
Временно 27
Временно отсутствовало из числа постоянного
населения 17
В течение года
Родилось детей у постоянных жителей города 8
Умерло из числа постоянных жителей города 5
Прибыло на постоянное жительство из других
городов и сельской местности 10
Выбыло на постоянное жительство в другие города
и сельские местности из числа постоянных жителей
города 4
На конец года:
Временно проживало 27
Временно отсутствовало из числа постоянного
населения 27
|
Решение:
а) Наличное население (лица, фактически находящиеся на момент переписи в данном населенном пункте, включая временно проживающих), а
постоянное население (лица, для которых данный населенный пункт является местом постоянного проживания, включая временно отсутствующих).
Постоянное население:
На начало года – 370-27+17=360 чел.
На конец года – 370+8-5+10-4-27+27=379 чел.
Наличное население:
На начало года – 370 чел.
На конец года – 370+8-5+10-4=383 чел.
б) Вычислим коэффициенты рождаемости, смертности и естественного прироста населения;
1. Общий коэффициент рождаемости:
Кр
=N/S*1000 = 8/397*1000=20
где: N-число родившихся живых детей за анализируемый период;
S-средняя численность населения за тот же период.
2. Общий коэффициент смертности:
Kсм
=M/S*1000 = 5/397*1000=13
где: М – число умерших за анализируемый период.
3. Коэффициент естественного прироста:
Kе.пр.
=(N-M) / S*1000 = (8-5)/397*1000=7
Ке.пр.
= Kр
– Kсм
= 20-13=7
в) Определим показатели механического движения населения:
1. Коэффициент интенсивности прибытия населения:
Ки.п.
= П / S*1000 =10/397*1000=25
где П – число прибывших на постоянное жительство за анализируемый период.
2. Коэффициент интенсивности выбытия населения:
Ки.в.
= В / S*1000= 4/397*1000=10
где В - число лиц, выбывших с целью перемены места жительства.
3. Коэффициент механического прироста населения:
Км.пр.
= (П-В) /S*1000=(10-4)/397*1000=15
Км.пр.
= Ки.п.
– Ки.в.
* 1000= 25-10=15
Задача 5
На основании данных по предприятию определить:
1) изменение среднегодовой и среднедневной заработной платы в абсолютном и относительном выражении;
2) абсолютное изменение фонда оплаты труда за счет изменения среднегодовой заработной плата и среднесписочной численности рабочих. Оформить результаты анализа и сделать вывод.
Таблица 13 Исходные данные
| Показатели |
Предыдущий год |
Отчетный год |
| Годовой фонд заработной платы, тыс. руб. |
10700
|
15700
|
| Среднесписочная численность рабочих, чел. |
107
|
127
|
| Отработанные всеми рабочими человеко-дни, чел.-дн. |
28 700
|
32 700
|
Решение:
Для решения задачи используется следующая зависимость между средним уровнем оплаты труда (f), численностью работающих (T) и фондом заработной платы (F):

Таблица 14
| Показатели |
Предыдущий год |
Отчетный год |
Отклонение |
| абсол. |
относит. |
| Годовой фонд заработной платы, тыс. руб. |
10700 |
15700 |
5000,0 |
46,7 |
| Среднесписочная численность рабочих, чел. |
107 |
127 |
20,0 |
18,7 |
| Отработанные всеми рабочими человеко-дни, чел.-дн. |
28 700 |
32 700 |
4000,0 |
13,9 |
| Среднегодовая зарплата |
100,0 |
123,6 |
23,6 |
23,6 |
| Среднедневная зарплата |
0,4 |
0,5 |
0,1 |
28,8 |
Как видим из таблицы, среднегодовая заработная плата увеличилась в отчетном году по сравнению с предыдущим на 23,6 тыс.руб. или на 23,6%, а среднедневная - на 100 руб. или на 28.8%.
Влияние каждого фактора на изменение фонда заработной платы определяем следующим образом:
а) прирост или уменьшение фонда заработной платы в связи с изменением численности работающих по формуле:
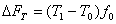 = (127-107)*100=2000
= (127-107)*100=2000
б) прирост или уменьшение фонда заработной платы за счет изменения уровня оплаты труда по формуле:
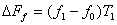 =(123,6-100)*127=2997,2
=(123,6-100)*127=2997,2
Таким образом, рост фонда заработной платы рабочих произошел в результате повышения уровня оплаты труда вследствие увеличения численности работающих.
Заключение
Экономическая статистика обеспечивает предоставление важной цифровой информации об уровне и возможностях развития страны: ее экономическом положении, уровне жизни населения, его составе и численности, рентабельности предприятий, динамике безработице и т.д. Статистическая информация является одним из решающих ориентиров государственной экономической политики.
Статистические методы используют комплексно (системно). Выделяют три основные стадии экономико-статистического исследования: сбор первичной статистической информации, статистическая сводка и обработка первичной информации, обобщение и интепретация статистической информации.
Изучив основные приемы исследования а также методику вычисления наиболее важных статистических величин, необходимо отметить, что конечная цель изучения статистики в целом - анализ изучаемого явления - крайне важен для всех сфер человеческой жизни. Анализ отображает явления в целом и вместе с этим учитывает влияние каждого фактора в отдельности. На основании проведенного анализа можно учитывать и прогнозировать факторы, негативно влияющие на развитие событий.
Список литературы
1. Башина О.Э. Общая теория статистики: Учебник - 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2007.
2. Башкатов Б.И., Рябушкин Б.Т. Практикум по национальному счетоводству. - М.: Финансы и статистика, 2004.
3. Курс социально-экономической статистики: учебник для вузов / Под ред. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ – ДАНА, 2000.
4. Микроэкономическая статистика: Учебник / Под ред. С.Д. Ильенковой – М.: Финансы и статистика, 2004.
5. Национальное счетоводство: Учебник / Под ред. Б.И. Башкатова – 2 изд., перераб. и доп. – М.: Финансы и статистика, 2002.
6. Региональная статистика: Учебник / Под ред. Е.В. Заровой, Г.И. Чудилина. – М.: Финансы и статистика, 2006.
7. Салин В.Н., Кудряшова С.И. Система национальных счетов: Учебное пособие. – М.: Финансы и статистика, 2006.
8. Салин В.Н., Медведев В.Г., Кудряшова С.И., Шпаковская Е.П. Макроэкономическая статистика: учебное пособие – 2-е изд., испр. – М.: Дело, 2001.
|