04.5. Основы расчета надежности технических систем по надежности их элементов
Целевое назначение и классификация методов расчета
Расчеты надежности
- расчеты, предназначенные для определения количественных показателей надежности. Они проводятся на различных этапах разработки, создания и эксплуатации объектов.
На этапе проектирования расчет надежности производится с целью прогнозирования (предсказания) ожидаемой надежности проектируемой системы. Такое прогнозирование необходимо для обоснования предполагаемого проекта, а также для решения организационно-технических вопросов:
- выбора оптимального варианта структуры;
- способа резервирования;
- глубины и методов контроля;
- количества запасных элементов;
- периодичности профилактики.
На этапе испытаний и эксплуатации расчеты надежности проводятся для оценки количественных показателей надежности. Такие расчеты носят, как правило, характер констатации. Результаты расчетов в этом случае показывают, какой надежностью обладали объекты, прошедшие испытания или используемые в некоторых условиях эксплуатации. На основании этих расчетов разрабатываются меры по повышению надежности, определяются слабые места объекта, даются оценки его надежности и влияния на нее отдельных факторов.
Многочисленные цели расчетов привели к большому их разнообразию. На рис. 4.5.1 изображены основные виды расчетов.
Элементный расчет
- определение показателей надежности объекта, обусловленных надежностью его комплектующих частей (элементов). В результате такого расчета оценивается техническое состояние объекта (вероятность того, что объект будет находиться в работоспособном состоянии, средняя наработка на отказ и т.п.).

Рис. 4.5.1. Классификация расчетов надежности
Расчет функциональной надежности - определение показателей надежности выполнения заданных функций (например, вероятность того, что система очистки газа будет работать заданное время, в заданных режимах эксплуатации с сохранением всех необходимых параметров по показателям очистки). Поскольку такие показатели зависят от ряда действующих факторов, то, как правило, расчет функциональной надежности более сложен, чем элементный расчет.
Выбирая на рис 4.5.1 варианты перемещений по пути, указанному стрелками, каждый раз получаем новый вид (случай) расчета.
Самый простой расчет
- расчет, характеристики которого представлены на рис. 4.5.1 слева: элементный расчет аппаратурной надежности простых изделий, нерезервированных, без учета восстановлений работоспособности при условии, что время работы до отказа подчинено экспоненциальному распределению.
Самый сложный расчет
- расчет, характеристики которого представлены на рис. 4.5.1 справа: функциональной надежности сложных резервированных систем с учетом восстановления их работоспособности и различных законов распределения времени работы и времени восстановления.
Выбор того или иного вида расчета надежности определяется заданием на расчет надежности. На основании задания и последующего изучения работы устройства (по его техническому описанию) составляется алгоритм расчета надежности, т.е. последовательность этапов расчета и расчетные формулы.
Последовательность расчета систем
Последовательность расчета системы представлена на рис. 4.5.2. Рассмотрим основные ее этапы.

Рис. 4.5.2. Алгоритм расчета надежности
Прежде всего четко следует сформулировать задание на расчет надежности. В нем должны быть указаны: 1) назначение системы ее состав и основные сведения о функционировании; 2) показатели надежности и признаки отказов, целевое назначение расчетов; 3) условия, в которых работает (или будет работать) система; 4) требования к точности и достоверности расчетов, к полноте учета действующих факторов.
На основании изучения задания делается вывод о характере предстоящих расчетов. В случае расчета функциональной надежности осуществляется переход к этапам 4-5-7, в случае расчета элементов (аппаратурной надежности) - к этапам 3-6-7.
Под структурной схемой надежности понимается наглядное представление (графическое или в виде логических выражений) условий, при которых работает или не работает исследуемый объект (система, устройство, технический комплекс и т.д.). Типовые структурные схемы представлены на рис. 4.5.3.

Рис. 4.5.3. Типовые структуры расчета надежности
Простейшей формой структурной схемы надежности является параллельно-последовательная структура. На ней параллельно соединяются элементы, совместный отказ которых приводит к отказу
В последовательную цепочку соединяются такие элементы, отказ любого из которых приводит к отказу объекта.
На рис. 4.5.3,а представлен вариант параллельно-последовательной структуры. По этой структуре можно сделать следующее заключение. Объект состоит из пяти частей. Отказ объекта наступает тогда, когда откажет или элемент 5, или узел, состоящий из элементов 1-4. Узел может отказать тогда, когда одновременно откажет цепочка, состоящая из элементов 3,4 и узел, состоящий из элементов 1,2. Цепь 3-4 отказывает, если откажет хотя бы один из составляющих ее элементов, а узел 1,2 - если откажут оба элемента, т.е. элементы 1,2. Расчет надежности при наличии таких структур отличается наибольшей простотой и наглядностью. Однако не всегда удается условие работоспособности представить в виде простой параллельно-последовательной структуры. В таких случаях используют или логические функции, или графы и ветвящиеся структуры, по которым оставляются системы уравнений работоспособности.
На основе структурной схемы надежности составляется набор расчетных формул. Для типовых случаев расчета используются формулы, приведенные в справочниках по расчетам надежности, стандартах и методических указаниях. Прежде чем применять эти формулы, необходимо предварительно внимательно изучить их существо и области использования.
Расчет надежности, основанный на использовании параллельно-последовательных структур
Пусть некоторая техническая система в составлена из n элементов (узлов). Допустим, надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом.
Параллельно-последовательная структура надежности сложного изделия дает представление о связи между надежностью изделия и надежностью его элементов. Расчет надежности ведется последовательно - начиная от расчета элементарных узлов структуры к ее все более сложным узлам. Например, в структуре рис. 5.3,а узел, состоящий из элементов 1-2 - элементарный узел, состоящий из элементов 1-2-3-4, сложный. Эта структура может быть сведена к эквивалентной, состоящей из элементов 1-2-3-4 и элемента 5, соединенных последовательно. Расчет надежности в данном случае сводится к расчету отдельных участков схемы, состоящих из параллельно и последовательно соединенных элементов.
Система с последовательным соединением элементов
Самым простым случаем в расчетном смысле является последовательное соединение элементов системы. В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы и называем такое соединение "последовательным" (рис. 4.5.4). Следует пояснить, что "последовательным" такое соединение элементов является только в смысле надежности, физически они могут быть соединены как угодно.

Рис. 4.5.4. Блок-схема системы с последовательным соединением элементов
С позиции надежности, такое соединение означает, что отказ устройства, состоящего из этих элементов, происходит при отказе элемента 1 или элемента 2, или элемента 3, или элемента n. Условие работоспособности можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 и элемент 2, и элемент 3, и элемент n.
Выразим надежность данной системы через надежности ее элементов. Пусть имеется некоторый промежуток времени (0,t), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности Р(t), нам важно знать значение этой надежности при t=t, т.е. Р(t). Это не функция, а определенное число; отбросим аргумент t и обозначим надежность системы просто Р. Аналогично обозначим надежности отдельных элементов P1
, P2
, P3
, ..., Pn
.
Для безотказной работы простой системы в течение времени t нужно, чтобы безотказно работал каждый из ее элементов. Обозначим S - событие, состоящее в безотказной работе системы за время t; s1
, s2
, s3
, ..., sn
- события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий s1
, s2
, s3
, ..., sn
:
S = s1
×s2
×s3
×...×sn
.
Предположим, что элементы s1
, s2
, s3
, ..., sn
отказывают независимо друг от друга (или, как говорят применительно к надежности, "независимы по отказам", а совсем кратко "независимы"). Тогда по правилу умножения вероятностей для независимых событий Р(S)=P(s1
)×P(s2
)×P(s3
)×...×P(sn
) или в других обозначениях,
Р = Р1
×Р2
×Р3
×...×Рn
., (4.5.1)
а короче P = 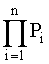 , (4.5.2) , (4.5.2)
т.е. надежность (вероятность работоспособного состояния) простой системы, составленной из независимых по отказам, последовательно соединенных элементов, равна произведению надежностей ее элементов.
В частном случае, когда все элементы обладают одинаковой надежностью P1
=P2
=P3
= ... =Pn
, выражение (4.5.2) принимает вид
Р = Pn
. (4.5.3)
Пример 4.5.1. Система состоит из 10 независимых элементов, надежность каждого из которых равна Р=0,95. Определить надежность системы.
По формуле (4.5.3) Р = 0,9510
» 0,6.
Из примера видно, как резко падает надежность системы при увеличении в ней числа элементов. Если число элементов n велико, то для обеспечения хотя бы приемлемой надежности Р системы каждый элемент должен обладать очень высокой надежностью.
Поставим вопрос: какой надежностью Р должен обладать отдельный элемент для того, чтобы система, составленная из n таких элементов, обладала заданной надежностью Р?
Из формулы (4.5.3) получим:
Р = 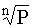 . .
Пример 4.5.2. Простая система состоит из 1000 одинаково надежных, независимых элементов. Какой надежностью должен обладать каждый из них для того, чтобы надежность системы была не меньше 0,9?
По формуле (4.5.4) Р =  ; lgР = lg0,91/1000
; Р»0,9999. ; lgР = lg0,91/1000
; Р»0,9999.
Интенсивность отказов системы при экспоненциальном законе распределения времени до отказа легко определить из выражения
lс
= l1
+ l2
+ l3
+ ... + ln
, (4.5.4)
т.е. как сумму интенсивностей отказов независимых элементов. Это и естественно, так как для системы, в которой элементы соединены последовательно, отказ элемента равносилен отказу системы, значит все потоки отказов отдельных элементов складываются в один поток отказов системы с интенсивностью, равной сумме интенсивностей отдельных потоков.
Формула (4.5.4) получается из выражения
Р = P1
P2
P3
... Pn
= ехр{-(l1
+ l2
+ l3
+ ... + ln
)}. (4.5.5)
Среднее время работы до отказа
Т0
= 1/lс
. (4.5.6)
Пример 4.5.3. Простая система S состоит из трех независимых элементов, плотности распределения времени безотказной работы которых заданы формулами:
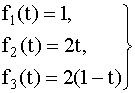 при 0 < t < 1 (рис. 4.5.5). при 0 < t < 1 (рис. 4.5.5).
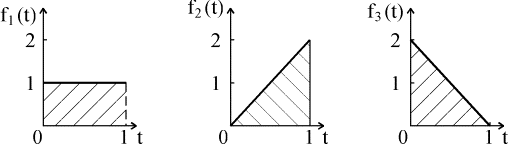
Рис. 4.5.5. Плотности распределения времени безотказной работы
Найти интенсивность отказов системы.
Решение. Определяем ненадежность каждого элемента:
 при 0 < t < 1. при 0 < t < 1.
Отсюда надежности элементов:
 при 0 < t < 1. при 0 < t < 1.
Интенсивности отказов элементов (условная плотность вероятности отказов) - отношение f(t) к р(t):
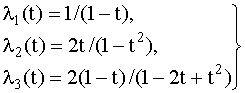 при 0 < t < 1. при 0 < t < 1.
Складывая, имеем: lс
= l1
(t) + l2
(t) + l3
(t).
Пример 4.5.4. Предположим, что для работы системы с последовательным соединением элементов при полной нагрузке необходимы два разнотипных насоса, причем насосы имеют постоянные интенсивности отказов, равные соответственно l1
=0,0001ч-1
и l2
=0,0002ч-1
. Требуется вычислить среднее время безотказной работы данной системы и вероятность ее безотказной работы в течение 100ч. Предполагается, что оба насоса начинают работать в момент времени t=0.
С помощью формулы (4.5.5) находим вероятность безотказной работы Ps
заданной системы в течение 100ч:
Ps
(t)=  . .
Ps
(100)=е-(0,0001+0,0002)
×
100
=0,97045.
Используя формулу (4.5.6), получаем
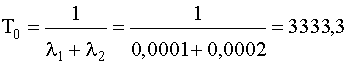 ч. ч.
Система с параллельным соединением элементов
На рис. 4.5.6 представлено параллельное соединение элементов 1, 2, 3. Это означает, что устройство, состоящее из этих элементов, переходит в состояние отказа после отказа всех элементов при условии, что все элементы системы находятся под нагрузкой, а отказы элементов статистически независимы.
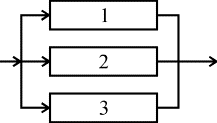
Рис. 4.5.6. Блок-схема системы с параллельным соединением элементов
Условие работоспособности устройства можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 или элемент 2, или элемент 3, или элементы 1 и 2, 1; и 3, 2; и 3, 1; и 2; и 3.
Вероятность безотказного состояния устройства, состоящего из n параллельно соединенных элементов определяется по теореме сложения вероятностей совместных случайных событий как
Р=(р1
+р2
+...рn
)-(р1
р2
+р1
р3
+...)-(р1
р2
р3
+р1
р2
рn
+...)-... ± (р1
р2
р3
...рn
). (4.5.7)
Для приведенной блок-схемы (рис. 4.5.6), состоящей из трех элементов, выражение (4.5.7) можно записать:
Р=р1
+р2
+р3
-(р1
р2
+р1
р3
+р2
р3
)+р1
р2
р3
.
Применительно к проблемам надежности, по правилу умножения вероятностей независимых (в совокупности) событий, надежность устройства из n элементов вычисляется по формуле
Р = 1- 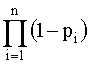 , (4.5.8) , (4.5.8)
т.е. при параллельном соединении независимых (в смысле надежности) элементов их ненадежности (1-pi
=qi
) перемножаются.
В частном случае, когда надежности всех элементов одинаковы, формула (4.5.8) принимает вид
Р = 1 - (1-р)n
. (4.5.9)
Пример 4.5.5. Предохранительное устройство, обеспечивающее безопасность работы системы под давлением, состоит из трех дублирующих друг друга клапанов. Надежность каждого из них р=0,9. Клапаны независимы в смысле надежности. Найти надежность устройства.
Решение. По формуле (4.5.9) Р=1-(1-0,9)3
=0,999.
Интенсивность отказов устройства состоящего из n параллельно соединенных элементов, обладающих постоянной интенсивностью отказов l0
, определяется как
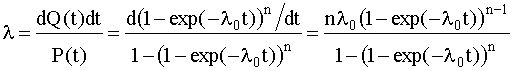 . (4.5.10) . (4.5.10)
Из (4.5.10) видно, что интенсивность отказов устройства при n>1 зависит от t: при t=0 она равна нулю, при увеличении t, монотонно возрастает до l0
.
Если интенсивности отказов элементов постоянны и подчинены показательному закону распределения, то выражение (4.5.8) можно записать
Р(t) = 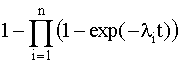 . (4.5.11) . (4.5.11)
Среднее время безотказной работы системы Т0
находим, интегрируя уравнение (4.5.11) в интервале [0,¥]:
Т0
= 
=(1/l1
+1/l2
+…+1/ln
)-(1/(l1
+l2
)+ 1/(l1
+l3
)+…)+ (4.5.12)
+(1/(l1
+l2
+l3
)+1/(l1
+l2
+l4
)+…)+(-1)n+1
´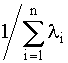 . .
В случае, когда интенсивности отказов всех элементов одинаковы, выражение (4.5.12) принимает вид
Т0
= 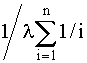 . (4.5.13) . (4.5.13)
Среднее время работы до отказа также можно получить, интегрируя уравнение (4.5.7) в интервале [0,¥]
Пример 4.5.6. Предположим, что два одинаковых вентилятора в системе очистки отходящих газов работают параллельно, причем если один из них выходит из строя, то другой способен работать при полной системной нагрузке без изменения своих надежностных характеристик.
Требуется найти безотказность системы в течение 400ч (продолжительность выполнения задания) при условии, что интенсивности отказов двигателей вентиляторов постоянны и равны l=0,0005ч-1
, отказы двигателей статистически независимы и оба вентилятора начинают работать в момент времени t=0.
Решение. В случае идентичных элементов формула (4.5.11) принимает вид
Р(t) = 2еxp(-lt) - еxp(-2lt).
Поскольку l = 0,0005 ч-1
и t = 400 ч, то
Р(400)
= 2еxp(-0,0005´400) - еxp(-2´0,0005´400)=0,9671.
Среднюю наработку на отказ находим, используя (4.5.13):
Т0
= 1/l(1/1 + 1/2) = 1/l´3/2 = 1,5/0,0005 = 3000 ч.
Способы преобразования сложных структур
Относительная простота расчетов надежности, основанных на использовании параллельно-последовательных структур, делают их самыми распространенными в инженерной практике. Однако не всегда условие работоспособности можно непосредственно представить параллельно-последовательной структурой. В этом случае можно сложную структуру заменить ее эквивалентной параллельно-последовательной структурой. К таким преобразованиям относится:
- преобразование с эквивалентной заменой треугольника на звезду и обратно;
- разложение сложной структуры по базовому элементу.
Существо способа преобразования с помощью эквивалентной замены треугольника на звезду и обратно заключается в том, что узел сложной конфигурации заменяется на узел другой, более простой конфигурации, но при этом подбираются такие характеристики нового узла, что надежности преобразуемой цепи сохранялись прежними.
Пусть, например, требуется заменить треугольник (рис. 4.5.7,а) звездой (рис. 4.5.7,б) при условии, что вероятность отказа элемента a
равна q13
, элемента b
равна q12
, элемента c
- q23
. Переход к соединению звездой не должен изменить надежность цепей 1-2, 1-3, 2-3. Поэтому значение вероятностей отказов элементов звезды q1
, q2
, q3
должны удовлетворять следующим равенствам:
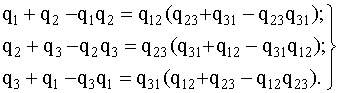 (4.5.14) (4.5.14)
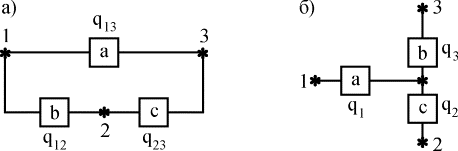
Рис. 4.5.7. Преобразование "треугольник - звезда"
Если пренебречь произведениями вида qi
qj
; qi
qj
qk
, то в результате решения системы уравнения (4.5.14) можно записать:
q1
=q12
q31
; q2
=q23
q12
; q3
=q31
q23
. (4.5.15)
Для обратного преобразования звезды в треугольник
q12
= 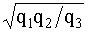 ; q23
= ; q23
= 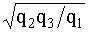 ; q31
= ; q31
= 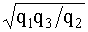 . (4.5.16) . (4.5.16)
Пример 4.5.7. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9, а вероятности отказов равны 0,1.
Решение.
1. Преобразуем соединение элементов 1,2,5 в треугольник (рис. 4.5.8,а), в звезду (рис. 4.5.8, б).
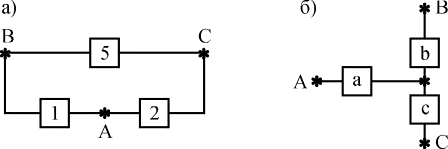
Рис. 4.5.8. К примеру преобразования структуры
2. Определим эквивалентные значения вероятности отказов для новых элементов a, b, c
qa
=q1
q2
=0,1´0,1 = 0,01;
qb
=q1
q5
=0,1´0,1 = 0,01;
qс
=q2
q5
=0,1´0,1 = 0,01.
3. Определим значения вероятности безотказного состояния элементов эквивалентной схемы (рис. 4.5.8,б)
pa
= pb
= pc
= 0,99.
4. Определим вероятность безотказной работы эквивалентного устройства (рис. 4.5.9):
Р = рa
(рb
р3
+ рc
р4
- рb
р3
рc
р4
) =
= 0,99(0,99´0,9+0,99´0,9 - 0,99´0,9´0,99´0,9) = 0,978.
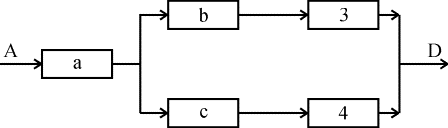
Рис. 4.5.9. Преобразованная структура
Способ преобразования с помощью разложения сложной структуры по некоторому базовому элементу основан на использовании теоремы о сумме вероятностей несовместных событий. В сложной структуре выбирают базовый элемент (или группу базовых элементов) и делаются следующие допущения:
- базовый элемент находится в работоспособном состоянии;
- базовый элемент находится в отказавшем состоянии.
Для этих случаев, представляющих собой два несовместных события, исходная структура преобразовывается в две новые схемы. В первой из них вместо базового элемента ставится "короткое замыкание" цепи, а во второй - разрыв. Вероятности безотказной работы каждой из полученных простых структур вычисляются и умножаются: первая - на вероятность безотказного состояния базового элемента, вторая - на вероятность отказа базового элемента. Полученные произведения складываются. Сумма равна искомой вероятности безотказной работы сложной структуры.
Пример 4.5.8. Решить предыдущий пример методом разложения сложной структуры.
Решение.
1. В качестве базового элемента примем элемент 5 (рис. 4.5.3,б).
2. Закоротим базовый элемент, т.е. сделаем допущение об абсолютной его проводимости. Присоединим к полученной структуре последовательно базовый элемент с характеристикой его надежности р5
. В результате вместо исходной структуры получим новую структуру (рис. 4.5.10,а).
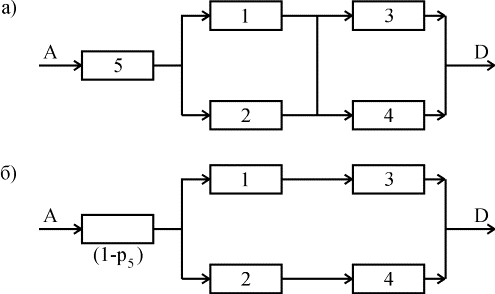
Рис. 4.5.10. Пример разложения мостиковой структуры по базовому элементу
3. Произведем обрыв базового элемента, т.е. сделаем предположение об его абсолютной ненадежности (непроводимости). К полученной структуре присоединим последовательно базовый элемент с характеристикой его ненадежности (1-р5
). В результате получим структуру (рис. 4.5.10,б).
4. Искомая вероятность равна сумме вероятностей структур (рис. 4.5.10,а,б), каждая из которых параллельно-последовательная. Поэтому
Р = р5
[(р1
+р2
-р1
р2
)(р3
+р4
-р3
р4
)] + (1-р5
)[р1
р3
+р2
р4
-р1
р3
р2
р4
]=
= 0,9[(0,9+0,9 - 0,9´0,9) ´ (0,9+0,9 - 0,9´0,9)] +
+ (1-0,9) ´ [0,9´0,9 + 0,9´0,9 - 0,9´0,9´0,9´0,9]»0,978.
Вероятность безотказной работы мостиковой схемы, состоящей из пяти неодинаковых и независимых элементов, можно определить по формуле:
Р=2р1
р2
р3
р4
р5
-р2
р3
р4
р5
-р1
р3
р4
р5
-р1
р2
р4
р5
-р1
р2
р3
р5
-
-р1
р2
р3
р4
+р1
р3
р5
+р2
р3
р4
+р1
р4
+р2
р5
. (4.5.17)
В случае идентичных элементов эта формула принимает вид
Р = 2р5
-5р4
+2р3
+2р2
. (4.5.18)
Подставляя соотношение (4.5.18) в формулу (4.5.4), получаем, что в случае использования элементов с постоянной интенсивностью отказов (экспоненциальном законе распределения отказов)
Р(t) = 2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt). (4.5.19)
Среднее время безотказной работы системы Т0
находим, путем интегрирования уравнения (5.19) в интервале [0,¥]:
Т0
= 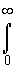 2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt)dt= 2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt)dt=
= (49/60)´(1/l). (4.5.20)
Пример 4.5.9. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9.
Решение.
Так как все элементы идентичны, воспользуемся формулой (4.5.18); с ее помощью получаем:
Р = 2´0,95
- 5´0,94
+2´0,93
+ 2´0,92
»0,978.
Пример 4.5.10. Требуется определить вероятность безотказной работы и среднюю наработку на отказ системы, состоящей из пяти независимых и одинаковых элементов, соединенных по мостиковой схеме (рис. 4.5.3,б); считается, что l=0,0005ч-1
, t=100ч и все элементы начинают работать в момент времени t=0.
Решение.
1. С помощью формулы (4.5.19) получаем
Р(100)
= 2е-0,25
-5е-0,2
+2е-0,15
+2е-0,1
= 0,9999.
2. Подставляя полученное значение вероятности безотказной работы в формулу (4.5.20), находим среднюю наработку на отказ
Т0
= 49/(60´0,0005) = 1633,4 ч.
Надежность резервированной системы
Одним из путей повышения надежности системы является введение в нее резервных (дублирующих) элементов. Резервные элементы включаются в систему как бы "параллельно" тем, надежность которых недостаточна.
Параллельное соединение резервного оборудования системы
Рассмотрим самый простой пример резервированной системы - параллельное соединение резервного оборудования системы. В этой схеме все n
одинаковых образцов оборудования работают одновременно, и каждый образец оборудования имеет одинаковую интенсивность отказов. Такая картина наблюдается, например, если все образцы оборудования держатся под рабочим напряжением (так называемый "горячий резерв"), а для исправной работы системы должен быть исправен хотя бы один из n
образцов оборудования.
В этом варианте резервирования применимо правило определения надежности параллельно соединенных независимых элементов. В нашем случае, когда надежности всех элементов одинаковы, надежность блока определяется по формуле (4.5.9)
Р = 1 - (1-р)n
.
Если система состоит из n
образцов резервного оборудования с различными интенсивностями отказов, то
P(t) = 1-(1-p1
) (1-p2
)... (1-pn
). (4.5.21)
Выражение (4.5.21) представляется как биноминальное распределение. Поэтому ясно, что когда для работы системы требуется по меньшей мере k
исправных из n
образцов оборудования, то
P(t) = 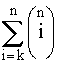 pi
(1-p)n-i
, где pi
(1-p)n-i
, где 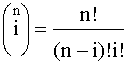 . (4.5.22) . (4.5.22)
При постоянной интенсивности отказов l элементов это выражение принимает вид
P(t) =  , (4.5.22.1) , (4.5.22.1)
где р = еxp(-lt).
Включение резервного оборудования системы замещением
В данной схеме включения n
одинаковых образцов оборудования только один находится все время в работе (рис. 4.5.11). Когда работающий образец выходит из строя, его непременно отключают, и в работу вступает один из (n
-1) резервных (запасных) элементов. Этот процесс продолжается до тех пор, пока все (n
-1) резервных образцов не будут исчерпаны.
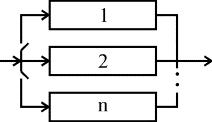
Рис. 4.5.11. Блок-схема системы включения резервного оборудования системы замещением
Примем для этой системы следующие допущения:
1. Отказ системы происходит, если откажут все n
элементов.
2. Вероятность отказа каждого образца оборудования не зависит от состояния остальных (n
-1) образцов (отказы статистически независимы).
3. Отказывать может только оборудование, находящееся в работе, и условная вероятность отказа в интервале t, t+dt равна ldt; запасное оборудование не может выходить из строя до того, как оно будет включено в работу.
4. Переключающие устройства считаются абсолютно надежными.
5. Все элементы идентичны. Резервные элементы имеют характеристики как новые.
Система способна выполнять требуемые от нее функции, если исправен по крайней мере один из n
образцов оборудования. Таким образом, в этом случае надежность равна просто сумме вероятностей состояний системы, исключая состояние отказа, т.е.
Р(t) = еxp(-lt) 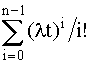 . (4.5.23) . (4.5.23)
В качестве примера рассмотрим систему, состоящую из двух резервных образцов оборудования, включаемых замещением. Для того чтобы эта система работала, в момент времени t, нужно, чтобы к моменту t были исправны либо оба образца, либо один из двух. Поэтому
Р(t) = еxp(-lt) 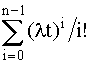 =(exp(-lt))(1+ lt). (4.5.24) =(exp(-lt))(1+ lt). (4.5.24)
На рис. 4.5.12 показан график функции Р(t) и для сравнения приведен аналогичный график для нерезервированной системы.
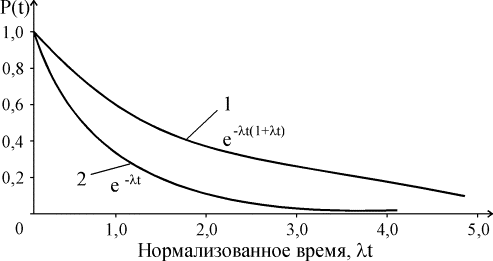 Рис. 4.5.12. Функции надежности для дублированной системы с включением резерва замещением (1) и нерезервированной системы (2) Рис. 4.5.12. Функции надежности для дублированной системы с включением резерва замещением (1) и нерезервированной системы (2)
Пример 4.5.11. Система состоит из двух идентичных устройств, одно из которых функционирует, а другое находится в режиме ненагруженного резерва. Интенсивности отказов обоих устройств постоянны. Кроме того, предполагается, что в начале работы резервное устройство имеет такие же характеристики, как и новое. Требуется вычислить вероятность безотказной работы системы в течение 100 ч при условии, что интенсивности отказов устройств l=0,001 ч-1
.
Решение. С помощью формулы (4.5.23) получаем Р(t) = (exp(-lt))(1+ lt).
При заданных значениях t и l вероятность безотказной работы системы составляет
Р(t) = е-0,1
(1+0,1) = 0,9953.
Во многих случаях нельзя предполагать, что запасное оборудование не выходит из строя, пока его не включат в работу. Пусть l1
- интенсивность отказов работающих образцов, а l2
- резервных или запасных (l2
>0). В случае дублированной системы функция надежности имеет вид:
Р(t) = ехр(-(l1
+l2
)t) + 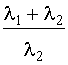 ехр(-l1
t) - ехр(-l1
t) - 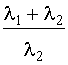 ехр(-(l1
+l2
)t). ехр(-(l1
+l2
)t).
Данный результат для k=2 можно распространить на случай k=n. Действительно
Р(t) = ехр(-l1
(1+a(n-1))t) 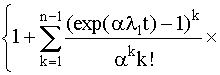 (4.5.25) (4.5.25)
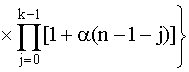 , где a = l2
/l1
> 0. , где a = l2
/l1
> 0.
Надежность резервированной системы в случае комбинаций отказов и внешних воздействий
В некоторых случаях отказ системы возникает вследствие определенных комбинаций отказов образцов входящих в систему оборудования и (или) из-за внешних воздействий на эту систему. Рассмотрим, например, метеоспутник с двумя передатчиками информации, один из которых является резервным или запасным. Отказ системы (потеря связи со спутником) возникает при выходе из строя двух передатчиков или в тех случаях, когда солнечная активность создает непрерывные помехи радиосвязи. Если интенсивность отказов работающего передатчика равна l, а j - ожидаемая интенсивность появления радиопомех, то функция надежности системы
Р(t) = еxp(-(l+j)t) + l t еxp(-(l+j)t). (4.5.26)
Данный тип модели также применим в случаях, когда резерв по схеме замещения отсутствует. Например, предположим, что нефтепровод подвергается гидравлическим ударам, причем воздействие незначительными гидроударами происходит с интенсивностью l, а значительными - с интенсивнностью j. Для разрыва сварных швов (из-за накопления повреждений) трубопроводу следует получить n малых гидроударов или один значительный.
Здесь состояние процесса разрушения представляется числом ударов (или повреждений), причем один мощный гидроудар равносилен n малых. Надежность или вероятность того, что трубопровод не будет разрушен действием микроударов к моменту времени t равна:
Р(t) = еxp(-(l+j)t) 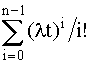 . (4.5.27) . (4.5.27)
Анализ надежности систем при множественных отказах
Рассмотрим метод анализа надежности нагруженных элементов в случае статистически независимых и зависимых (множественных) отказов. Следует заметить, что этот метод может быть применен и в случае других моделей и распределений вероятностей. При разработке этого метода предполагается, что для каждого элемента системы существует некоторая вероятность появления множественных отказов. Как известно, множественные отказы действительно существуют, и для их учета в соответствующие формулы вводится параметр a. Этот параметр может быть определен на основе опыта эксплуатации резервированных систем или оборудования и представляет собой долю отка
зов, вызываемых общей причиной.
Другими словами, параметр а можно рассматривать как точечную оценку вероятности того, что отказ некоторого элемента относится к числу множественных отказов. При этом можно считать, что интенсивность отказов элемента имеет две взаимоисключающие составляющие, т.
е. l=l1
+l2
, где l1
- постоянная интенсивность статистически независимых отказов элемента, l2
- интенсивность множественных отказов резервированной системы или элемента. Поскольку
a=l2
/l, то l2
=
a/ l, и следовательно, l1
=(1- a)l.
Приведем формулы и зависимости для вероятности безотказной работы, интенсивности отказов и средней наработки на отказ в случае систем с параллельным и последовательным соединением элементов, а также систем с k исправными элементами из п
и систем, элементы которых соединены по мостиковой схеме. Система с параллельным соединением элементов (рис. 4.5.13) - обычная параллельная схема, к которой последовательно подсоединен один элемент. Параллельная часть (I) схемы отображает независимые отказы в любой системе из n элементов, а последовательно соединенный элемент (II) - все множественные отказы системы. 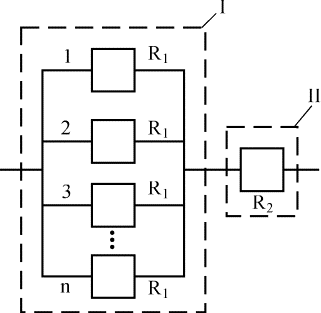 Рис. 4.5.13. Модифицированная система с параллельным соединением одинаковых элементов Гипотетический элемент, характеризуемый определенной вероятностью появления множественного отказа, последовательно соединен с элементами, которые характеризуются независимыми отказами. Отказ гипотетического последовательно соединенного элемента (т.е. множественный отказ) приводит к отказу всей системы. Предполагается, что все множественные отказы полностью взаимосвязаны. Вероятность безотказной работы такой системы определяется как Rр
={1-(1-R1
)n
}R2
, где n - число одинаковых элементов; R1
- вероятность безотказной работы элементов, обусловленная независимыми отказами; R2
- вероятность безотказной работы системы, обусловленная множественными отказами. При постоянных интенсивностях отказов l1
и l2
выражение для вероятности безотказной работы принимает вид Rр
(t)={1-(1-e-(1-
a
)
l
t
)n
}e-
al
t
, (4.5.28) Рис. 4.5.13. Модифицированная система с параллельным соединением одинаковых элементов Гипотетический элемент, характеризуемый определенной вероятностью появления множественного отказа, последовательно соединен с элементами, которые характеризуются независимыми отказами. Отказ гипотетического последовательно соединенного элемента (т.е. множественный отказ) приводит к отказу всей системы. Предполагается, что все множественные отказы полностью взаимосвязаны. Вероятность безотказной работы такой системы определяется как Rр
={1-(1-R1
)n
}R2
, где n - число одинаковых элементов; R1
- вероятность безотказной работы элементов, обусловленная независимыми отказами; R2
- вероятность безотказной работы системы, обусловленная множественными отказами. При постоянных интенсивностях отказов l1
и l2
выражение для вероятности безотказной работы принимает вид Rр
(t)={1-(1-e-(1-
a
)
l
t
)n
}e-
al
t
, (4.5.28)
где t - время. Влияние множественных отказов на надежность системы с параллельным соединением элементов наглядно демонстрируется с помощью рис. 4.5.14 – 4.5.16; при увеличении значения параметра a вероятность безотказной работы такой системы уменьшается. Параметр a принимает значения от 0 до 1. При a=0 модифицированная параллельная схема ведет себя как обычная параллельная схема, а при a=1 она действует как один элемент, т. е. все отказы системы являются множественными.
Поскольку интенсивность отказов и среднее время наработки на отказ любой системы можно определить с помощью (4.3.7) и формул
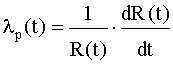 , ,
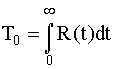 , ,
с учетом выражения для
Rр
(t) получаем, что интенсивность отказов (рис. 4.5.17) и средняя наработка на отказ модифицированной системы соответственно равны
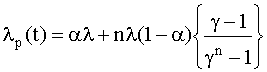 , (4.5.29) , (4.5.29)
 , где , где 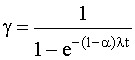 . (4.5.30) . (4.5.30)
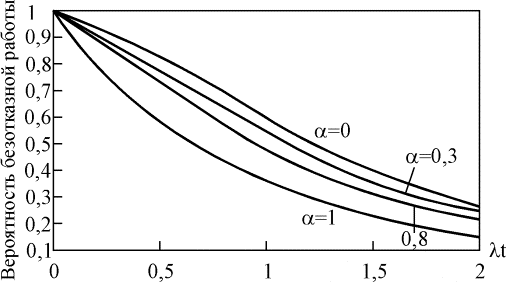 Рис. 4.5.14. Зависимость вероятности безотказной работы системы с параллельным соединением двух элементов от параметра a Рис. 4.5.14. Зависимость вероятности безотказной работы системы с параллельным соединением двух элементов от параметра a 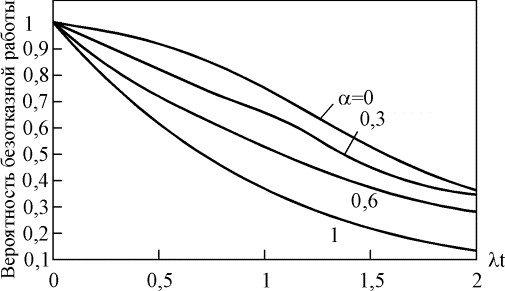 Рис. 4.5.15. Зависимость вероятности безотказной работы системы с параллельным соединением трех элементов от параметра a Рис. 4.5.15. Зависимость вероятности безотказной работы системы с параллельным соединением трех элементов от параметра a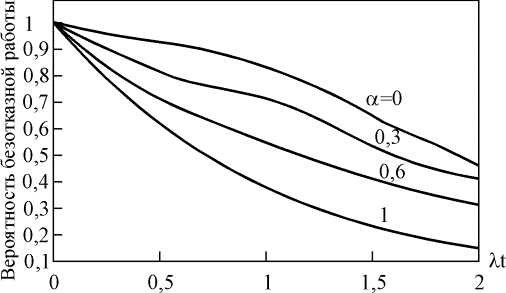 Рис. 4.5.16. Зависимость вероятности безотказной работы системы с параллельным соединением четырех элементов от параметра a Рис. 4.5.16. Зависимость вероятности безотказной работы системы с параллельным соединением четырех элементов от параметра a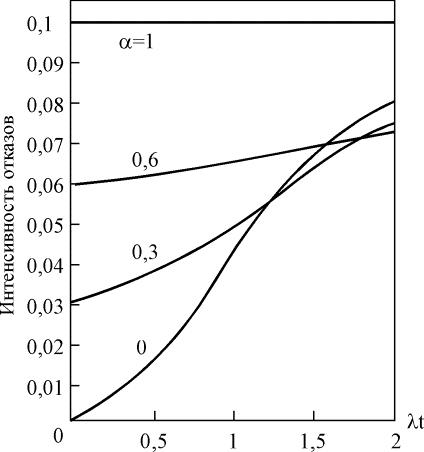 Рис. 4.5.17. Зависимость интенсивности отказов системы с параллельным соединением четырех элементов от параметра a Пример 4.5.12. Требуется определить вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, если l=0,001 ч-1
; a=0,071; t=200 ч. Вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, для которой характерны множественные отказы, равна 0,95769. Вероятность безотказной работы системы, состоящей из двух параллельно соединенных элементов и характеризуемой только независимыми отказами, равна 0,96714. Система с k исправными элементами из п одинаковых элементов включает в себя гипотетический элемент, соответствующий множественным отказам и соединенный последовательно с обычной системой типа k из n, для которой характерны независимые отказы. Отказ, отображаемый этим гипотетическим элементом, вызывает отказ всей системы. Вероятность безотказной работы модифицированной системы с k исправными элементами из n можно вычислить по формуле Рис. 4.5.17. Зависимость интенсивности отказов системы с параллельным соединением четырех элементов от параметра a Пример 4.5.12. Требуется определить вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, если l=0,001 ч-1
; a=0,071; t=200 ч. Вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, для которой характерны множественные отказы, равна 0,95769. Вероятность безотказной работы системы, состоящей из двух параллельно соединенных элементов и характеризуемой только независимыми отказами, равна 0,96714. Система с k исправными элементами из п одинаковых элементов включает в себя гипотетический элемент, соответствующий множественным отказам и соединенный последовательно с обычной системой типа k из n, для которой характерны независимые отказы. Отказ, отображаемый этим гипотетическим элементом, вызывает отказ всей системы. Вероятность безотказной работы модифицированной системы с k исправными элементами из n можно вычислить по формуле
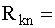 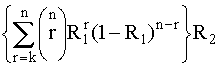 , (4.5.31) , (4.5.31)
где R1
- вероятность безотказной работы элемента, для которого характерны независимые отказы; R2
- вероятность безотказной работы системы с k исправными элементами из n, для которой характерны множественные отказы. При постоянных интенсивностях l1
и l2
полученное выражение принимает вид
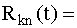 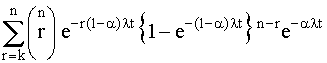 . (4.5.32) . (4.5.32)
Зависимость вероятности безотказной работы от параметра a для систем с двумя исправными элементами из трех и двумя и тремя исправными элементами из четырех показаны на рис. 4.5.18 - 4.5.20. При увеличении параметра a вероятность безотказной работы системы уменьшается на небольшую величину (lt). 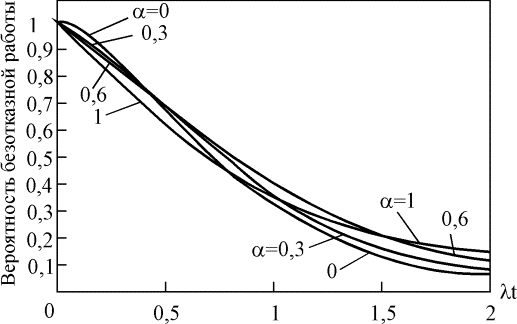 Рис. 4.5.18. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из n элементов Рис. 4.5.18. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из n элементов 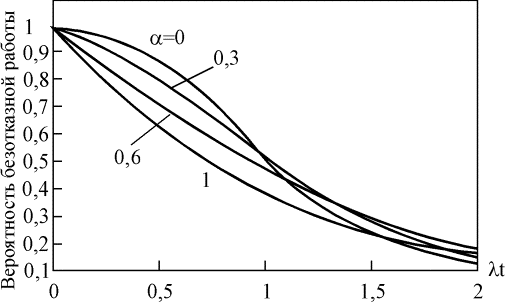 Рис. 4.5.19. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из четырех элементов Рис. 4.5.19. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из четырех элементов 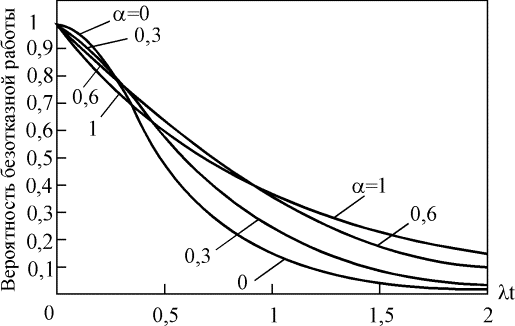 Рис. 4.5.20. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе трех из четырех элементов Интенсивность отказов системы с k исправными элементами из n и средняя наработка на отказ могут быть определены следующим образом: Рис. 4.5.20. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе трех из четырех элементов Интенсивность отказов системы с k исправными элементами из n и средняя наработка на отказ могут быть определены следующим образом:  , (4.5.33) , (4.5.33)
где h = {1-e-(1-
b
)
l
t
},
q = e(r
a
-r-
a
)
l
t
и
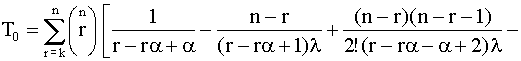
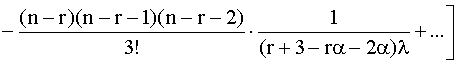 . (4.5.34) . (4.5.34)
Пример 4.5.13. Требуется определить вероятность безотказной работы системы с двумя исправными элементами из трех, если l=0,0005 ч-1
; a=0,3; t=200 ч. С помощью выражения для Rkn
находим, что вероятность безотказной работы системы, в которой происходили множественные отказы, составляет 0,95772. Отметим, что для системы с независимыми отказами эта вероятность равна 0,97455. Система с параллельно-последовательным соединением элементов соответствует системе, состоящей из одинаковых элементов, для которых характерны независимые отказы, и ряда ветвей, содержащих воображаемые элементы, для которых характерны множественные отказы. Вероятность безотказной работы модифицированной системы с параллельно-последовательным (смешанным) соединением элементов можно определить с помощью формулы Rps
={1-(1- 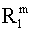 )n
}R2
, где m - число одинаковых элементов в ответвлении, n - число одинаковых ответвлений. )n
}R2
, где m - число одинаковых элементов в ответвлении, n - число одинаковых ответвлений.
При постоянных интенсивностях отказов l1
и l2
это выражение принимает вид
Rрs
(t) = [1-(1-e-n(1-
a
)
l
t
)m
}e-
al
t
. (4.5.35)
Интенсивность отказов системы с параллельно-последовательным соединением элементов и средняя наработка на отказ могут быть определены следующим образом:
lps
(t)=al+mn(1-a)l , (4.5.36)где l=1/[1-e-n(1-
g
)
l
t
] и , (4.5.36)где l=1/[1-e-n(1-
g
)
l
t
] и
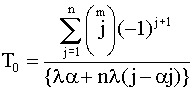 . (4.5.37) . (4.5.37)
Система, элементы которой соединены по мостиковой схеме,соответствует схеме, состоящей из одинаковых элементов, для которых характерны независимые отказы, и последовательно подсоединенного к ним воображаемого элемента, для которого характерны множественные отказы. При множественном отказе
гипотетического элемента вся система выходит из строя. Вероятность безотказной работы модифицированной системы с элементами, соединенными по мостиковой схеме
, можно вычислить по формуле
Rb
={1-2(1-R1
)5
+5(1-R1
)4
-2(1-R1
)3
-2(1-R1
)2
}R2
(4.5.38)
(здесь Rb
- вероятность безотказной работы мостиковой схемы, для которой характерны множественные отказы). Эта формула при постоянных интенсивностях l1
и l2
принимает вид
Rb
(t)=[1-2(1-e-At
)5
+5(1- e-At
)4
-2(1- e-At
)3
-2(1- e-At
)2
] e-
bl
t
. (4.5.39)
(здесь А=(1-a)l). Зависимость безотказной работы системы Rb
(t) для различных параметров a показана на рис. 4.5.21. При малых значениях lt вероятность безотказной работы системы с элементами, соединенными по мостиковой схеме, убывает с увеличением параметра a.  Рис. 4.5.21. Зависимость вероятности безотказной работы системы, элементы которой соединены по мостиковой схеме, от параметра a Рис. 4.5.21. Зависимость вероятности безотказной работы системы, элементы которой соединены по мостиковой схеме, от параметра a
Интенсивность отказов рассматриваемой системы и средняя наработка на отказ могут быть определены следующим образом:
lkn
(t)=bl+A(-8p5
+25p4
-24p3
+4p2
+4p)+  , (4.5.40) , (4.5.40)
где p=(1-e-At
) и
Т0
= 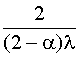 + + 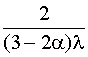 + + 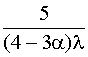 + + 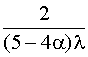 . (4.5.41) . (4.5.41)
Пример 4.5.14. Требуется вычислить вероятность безотказной работы в течение 200 ч для системы с одинаковыми элементами, соединенными по мостиковой схеме, если l=0,0005 ч-1
и a=0,3. Используя выражение для Rb
(t), находим, что вероятность безотказной работы системы с соединением элементов по мостиковой схеме составляет примерно 0,96; для системы с независимыми отказами (т.е. при a=0) эта вероятность равна 0,984.
Модель надежности системы с множественными отказами
Для анализа надежности системы, состоящей из двух неодинаковых элементов, для которых характерны множественные отказы, рассмотрим такую модель, при построении которой были сделаны следующие допущения и приняты следующие обозначения:
Допущения (1) множественные отказы и отказы других типов статистически независимы; (2) множественные отказы связаны с выходом из строя не менее двух элементов; (3) при отказе одного из нагруженных резервированных элементов отказавший элемент восстанавливается, при отказе обоих элементов восстанавливается вся система; (4) интенсивность множественных отказов и интенсивность восстановлений постоянны.
Обозначения
P0
(t) - вероятность того, что в момент времени t оба элемента функционируют;
P1
(t) - вероятность того, что в момент времени t элемент 1 вышел из строя, а элемент 2 функционирует;
P2
(t) - вероятность того, что в момент времени t эл
емент 2 вышел из строя, а элемент 1 функционирует;
P3
(t) - вероятность того, что в момент времени t элементы 1 и 2 вышли из строя;
P4
(t) - вероятность того, что в момент времени t имеются специалисты и запасные элементы для восстановления обоих элементов;
li
- постоянная интенсивность отказов элементов 1 и 2
(i=1,2);
mi
- постоянная интенсивность восстановлений элементов 1 и 2 (i=1,2);
m3
- постоянная интенсивность восстановлений элементов 1 и 2;
a - постоянный коэффициент, характеризующий наличие специалистов и запасных элементов;
b - постоянная интенсивность множественных отказов;
t -время.
Рассмотрим три возможных случая восстановления элементов при их одновременном отказе:
Случай 1. Запасные элементы, ремонтный инструмент и квалифицированные специалисты имеются для восстановления обоих элементов, т. е. элементы могут быть восстановлены одновременно.
Случай 2. Запасные элементы, ремонтный инструмент и квалифицированные специалисты имеются только для восстановления одного элемента, т. е. может быть восстановлен только один элемент. Случай 3. Запасные элементы, ремонтный инструмент и квалифицированные специалисты отсутствуют, и, кроме того, может существовать очередь на ремонтное обслуживание. Математическая модель системы, изображенной на рис. 4.5.22, представляет собой следующую систему дифференциальных уравнений первого порядка:
P'0
(t) = - 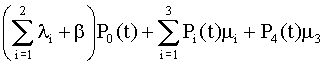 , ,
P'1
(t) = -(l2
+m1
)P1
(t)+P3
(t)m2
+P0
(t)l1
,
P'2
(t) = -(l1
+m2
)P2
(t)+P0
(t)l2
+P3
(t)m1
, (4.5.42)
P'3
(t) = - 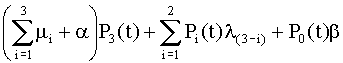 , ,
P'4
(t) = -m3
P4
(t)+P3
(t)a.
При t=0 имеем P0
(0)=1, а другие вероятности равны нулю.
 Рис. 4.5.22. Модель готовности системы в случае множественных отказов Приравнивая в полученных уравнениях производные по времени нулю, для установившегося режима получаем Рис. 4.5.22. Модель готовности системы в случае множественных отказов Приравнивая в полученных уравнениях производные по времени нулю, для установившегося режима получаем
-  , ,
-(l2
+m1
)P1
+P3
m2
+P0
l1
= 0,
-(l1
+m2
)P2
+P0
l2
+P3
m1
= 0, (4.5.43)
- 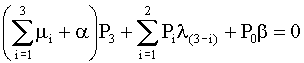 , ,
-m3
P4
+P3
a = 0,
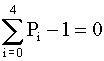 . .
Решая эту совместную систему уравнений, получаем
P0
= 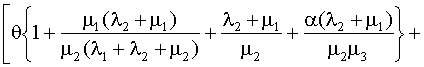
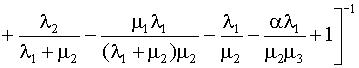 , (4.5.44) , (4.5.44)
где
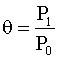 , ,
(P1
/P0
)= 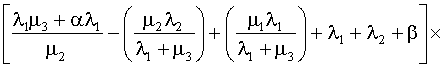
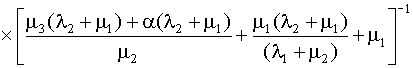 , (4.5.45) , (4.5.45)
P1
=qP0
,
P2
= 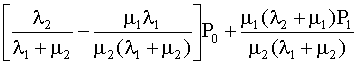 , ,
P3
= 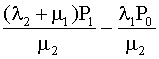 , ,
P4
= 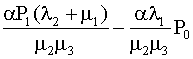 . .
Стационарный коэффициент готовности может быть вычислен по формуле
Kг
= 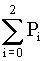 . .
|



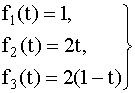 при 0 < t < 1 (рис. 4.5.5).
при 0 < t < 1 (рис. 4.5.5).
 при 0 < t < 1.
при 0 < t < 1. при 0 < t < 1.
при 0 < t < 1.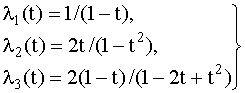 при 0 < t < 1.
при 0 < t < 1.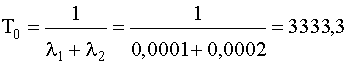 ч.
ч.
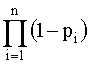 , (4.5.8)
, (4.5.8)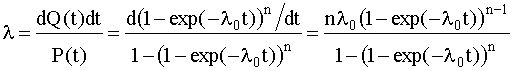 . (4.5.10)
. (4.5.10)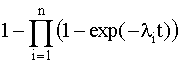 . (4.5.11)
. (4.5.11)
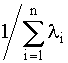 .
.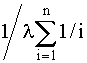 . (4.5.13)
. (4.5.13)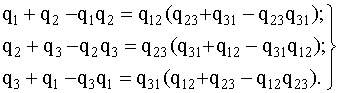 (4.5.14)
(4.5.14)



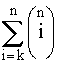 pi
(1-p)n-i
, где
pi
(1-p)n-i
, где 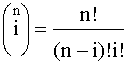 . (4.5.22)
. (4.5.22) , (4.5.22.1)
, (4.5.22.1)
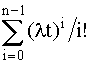 . (4.5.23)
. (4.5.23) Рис. 4.5.12. Функции надежности для дублированной системы с включением резерва замещением (1) и нерезервированной системы (2)
Рис. 4.5.12. Функции надежности для дублированной системы с включением резерва замещением (1) и нерезервированной системы (2) 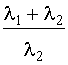 ехр(-l1
t) -
ехр(-l1
t) - 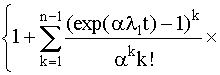 (4.5.25)
(4.5.25)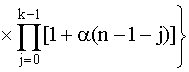 , где a = l2
/l1
> 0.
, где a = l2
/l1
> 0. Рис. 4.5.13. Модифицированная система с параллельным соединением одинаковых элементов Гипотетический элемент, характеризуемый определенной вероятностью появления множественного отказа, последовательно соединен с элементами, которые характеризуются независимыми отказами. Отказ гипотетического последовательно соединенного элемента (т.е. множественный отказ) приводит к отказу всей системы. Предполагается, что все множественные отказы полностью взаимосвязаны. Вероятность безотказной работы такой системы определяется как Rр
={1-(1-R1
)n
}R2
, где n - число одинаковых элементов; R1
- вероятность безотказной работы элементов, обусловленная независимыми отказами; R2
- вероятность безотказной работы системы, обусловленная множественными отказами. При постоянных интенсивностях отказов l1
и l2
выражение для вероятности безотказной работы принимает вид Rр
(t)={1-(1-e-(1-
a
)
l
t
)n
}e-
al
t
, (4.5.28)
Рис. 4.5.13. Модифицированная система с параллельным соединением одинаковых элементов Гипотетический элемент, характеризуемый определенной вероятностью появления множественного отказа, последовательно соединен с элементами, которые характеризуются независимыми отказами. Отказ гипотетического последовательно соединенного элемента (т.е. множественный отказ) приводит к отказу всей системы. Предполагается, что все множественные отказы полностью взаимосвязаны. Вероятность безотказной работы такой системы определяется как Rр
={1-(1-R1
)n
}R2
, где n - число одинаковых элементов; R1
- вероятность безотказной работы элементов, обусловленная независимыми отказами; R2
- вероятность безотказной работы системы, обусловленная множественными отказами. При постоянных интенсивностях отказов l1
и l2
выражение для вероятности безотказной работы принимает вид Rр
(t)={1-(1-e-(1-
a
)
l
t
)n
}e-
al
t
, (4.5.28)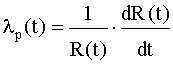 ,
,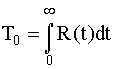 ,
,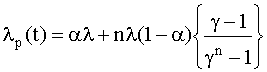 , (4.5.29)
, (4.5.29) , где
, где 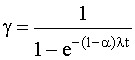 . (4.5.30)
. (4.5.30) Рис. 4.5.14. Зависимость вероятности безотказной работы системы с параллельным соединением двух элементов от параметра a
Рис. 4.5.14. Зависимость вероятности безотказной работы системы с параллельным соединением двух элементов от параметра a  Рис. 4.5.15. Зависимость вероятности безотказной работы системы с параллельным соединением трех элементов от параметра a
Рис. 4.5.15. Зависимость вероятности безотказной работы системы с параллельным соединением трех элементов от параметра a Рис. 4.5.16. Зависимость вероятности безотказной работы системы с параллельным соединением четырех элементов от параметра a
Рис. 4.5.16. Зависимость вероятности безотказной работы системы с параллельным соединением четырех элементов от параметра a Рис. 4.5.17. Зависимость интенсивности отказов системы с параллельным соединением четырех элементов от параметра a Пример 4.5.12. Требуется определить вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, если l=0,001 ч-1
; a=0,071; t=200 ч. Вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, для которой характерны множественные отказы, равна 0,95769. Вероятность безотказной работы системы, состоящей из двух параллельно соединенных элементов и характеризуемой только независимыми отказами, равна 0,96714. Система с k исправными элементами из п одинаковых элементов включает в себя гипотетический элемент, соответствующий множественным отказам и соединенный последовательно с обычной системой типа k из n, для которой характерны независимые отказы. Отказ, отображаемый этим гипотетическим элементом, вызывает отказ всей системы. Вероятность безотказной работы модифицированной системы с k исправными элементами из n можно вычислить по формуле
Рис. 4.5.17. Зависимость интенсивности отказов системы с параллельным соединением четырех элементов от параметра a Пример 4.5.12. Требуется определить вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, если l=0,001 ч-1
; a=0,071; t=200 ч. Вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, для которой характерны множественные отказы, равна 0,95769. Вероятность безотказной работы системы, состоящей из двух параллельно соединенных элементов и характеризуемой только независимыми отказами, равна 0,96714. Система с k исправными элементами из п одинаковых элементов включает в себя гипотетический элемент, соответствующий множественным отказам и соединенный последовательно с обычной системой типа k из n, для которой характерны независимые отказы. Отказ, отображаемый этим гипотетическим элементом, вызывает отказ всей системы. Вероятность безотказной работы модифицированной системы с k исправными элементами из n можно вычислить по формуле 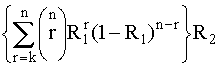 , (4.5.31)
, (4.5.31)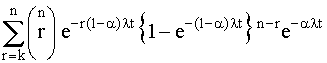 . (4.5.32)
. (4.5.32) Рис. 4.5.18. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из n элементов
Рис. 4.5.18. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из n элементов  Рис. 4.5.19. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из четырех элементов
Рис. 4.5.19. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из четырех элементов  Рис. 4.5.20. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе трех из четырех элементов Интенсивность отказов системы с k исправными элементами из n и средняя наработка на отказ могут быть определены следующим образом:
Рис. 4.5.20. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе трех из четырех элементов Интенсивность отказов системы с k исправными элементами из n и средняя наработка на отказ могут быть определены следующим образом:  , (4.5.33)
, (4.5.33) 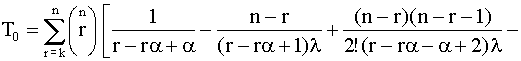
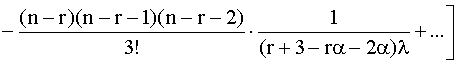 . (4.5.34)
. (4.5.34) , (4.5.36)где l=1/[1-e-n(1-
g
)
l
t
] и
, (4.5.36)где l=1/[1-e-n(1-
g
)
l
t
] и 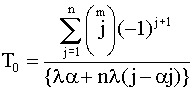 . (4.5.37)
. (4.5.37) Рис. 4.5.21. Зависимость вероятности безотказной работы системы, элементы которой соединены по мостиковой схеме, от параметра a
Рис. 4.5.21. Зависимость вероятности безотказной работы системы, элементы которой соединены по мостиковой схеме, от параметра a , (4.5.40)
, (4.5.40)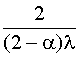 +
+ 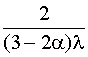 +
+ 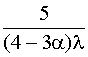 +
+ 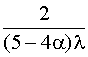 . (4.5.41)
. (4.5.41)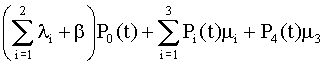 ,
,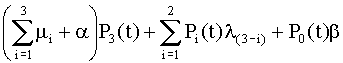 ,
, Рис. 4.5.22. Модель готовности системы в случае множественных отказов Приравнивая в полученных уравнениях производные по времени нулю, для установившегося режима получаем
Рис. 4.5.22. Модель готовности системы в случае множественных отказов Приравнивая в полученных уравнениях производные по времени нулю, для установившегося режима получаем  ,
,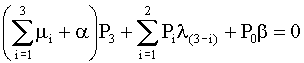 ,
,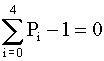 .
.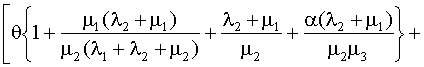
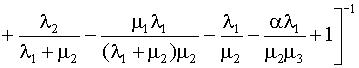 , (4.5.44)
, (4.5.44)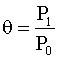 ,
,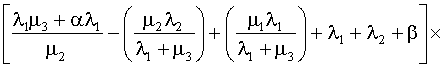
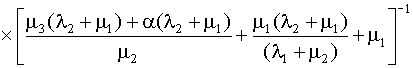 , (4.5.45)
, (4.5.45)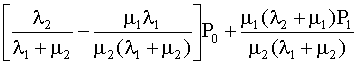 ,
,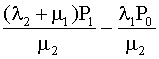 ,
,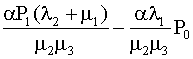 .
.