Содержание
Введение
Расчет операторной передаточной функции активного четырехполюсника
Параметрический синтез фильтра
Расчет частотных характеристик фильтра
Расчет переходной характеристики фильтра
Анализ полученных результатов
Список использованной литературы
Введение
Активные RC
-фильтры
Электрические фильтры, то есть устройства, пропускающие электрические колебания одних частот и задерживающие колебания других, широко применяются в современной промышленной электронике. Область частот пропускаемых колебаний, для которых модуль передаточной функции с заданной точностью равен некоторому определенному значению, называется полосой пропускания фильтра. Граничные частоты полосы пропускания принято называть частотами среза. Область частот задерживаемых колебаний, для которых модуль передаточной функции не превосходит некоторого установленного уровня, называется полосой задерживания. В связи с тем, что идеального разделения полос пропускания и задерживания добиться невозможно, говорят об области спада амплитудно-частотной характеристики (АЧХ) фильтра. В зависимости от взаимного расположения полос пропускания и задерживания (рис. 2) различают фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ), режекторные (заграждающие) фильтры (РФ).
В общем случае передаточную функцию фильтра с сосредоточенными параметрами можно записать в виде отношения двух рациональных выражений (полиномов):
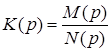 = = , ,
где  , , 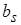 – вещественные числа; – вещественные числа;  – комплексная частота. Наибольшая степень – комплексная частота. Наибольшая степень 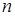 переменной переменной  в знаменателе в знаменателе 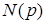 соответствует порядку фильтра. соответствует порядку фильтра.
 |
| Рис. 2 |
Особый интерес представляют фильтры первого и второго порядка, так как фильтры более высоких порядков строятся, как правило, на их основе. Для различного типа фильтров первого и второго порядков передаточные функции в дробно-рациональной форме приведены в табл. 1 (форма 1).
Таблица 1
Порядок
фильтра
|
Тип
фильтра
|
Коэффициент передачи фильтра |
| форма 1 |
форма 2 |
Фильтры
первого
порядка
|
ФНЧ
|
 |
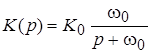 |
ФВЧ
|
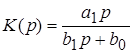 |
 |
Фильтры
второго
порядка
|
ФНЧ
|
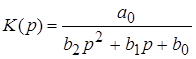 |
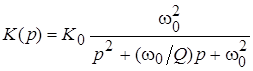 |
ФВЧ
|
 |
 |
ПФ
|
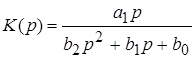 |
 |
РФ
|
 |
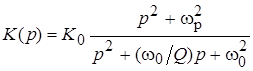 |
На практике при описании передаточных функций фильтров первого и второго порядков принято пользоваться такими параметрами, как коэффициент передачи фильтра в полосе пропускания  , характеристическая (собственная) частота , характеристическая (собственная) частота  = = , добротность , добротность  (для фильтров второго порядка), частота режекции (для фильтров второго порядка), частота режекции 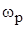 = =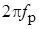 (для РФ). Выражения для передаточных функций, получаемые при использовании названных параметров, также приведены в табл. 1 (форма 2). Сравнение двух форм записи передаточных функций позволяет легко проследить связь параметров фильтров (для РФ). Выражения для передаточных функций, получаемые при использовании названных параметров, также приведены в табл. 1 (форма 2). Сравнение двух форм записи передаточных функций позволяет легко проследить связь параметров фильтров  , ,  , ,  , , 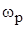 с коэффициентами с коэффициентами  , ,  , ,  , ,  , ,  , , 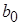 . .
Анализ установившегося режима при воздействии синусоидальных сигналов проводят, полагая  = =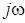 ( ( , , – циклическая и угловая частоты синусоидального колебания; – циклическая и угловая частоты синусоидального колебания;  = =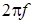 ). Имеющая при этом место зависимость модуля передаточной функции ). Имеющая при этом место зависимость модуля передаточной функции  от частоты является уравнением АЧХ фильтра. Обычно значение модуля передаточной функции выражается в децибелах: от частоты является уравнением АЧХ фильтра. Обычно значение модуля передаточной функции выражается в децибелах:
 [дБ]= [дБ]=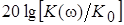 . .
Коэффициент передачи в полосе пропускания  в этой формуле соответствует частоте в этой формуле соответствует частоте  =0 для ФНЧ ( =0 для ФНЧ ( = = ), ),  ∞ для ФВЧ ( ∞ для ФВЧ ( = =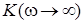 ), ),  = = для ПФ ( для ПФ ( = =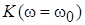 ). ).
Для РФ характерными являются коэффициенты передачи на частотах  =0 ( =0 ( = = ) и ) и  ∞ ( ∞ ( = =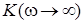 ). Причем выполняется соотношение ). Причем выполняется соотношение  = = . В случае симметричной АЧХ характеристическая частота РФ совпадает с частотой максимального затухания колебаний – частотой режекции ( . В случае симметричной АЧХ характеристическая частота РФ совпадает с частотой максимального затухания колебаний – частотой режекции ( = =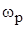 ), а коэффициенты передачи для нижнего и верхнего участков полосы пропускания равны ( ), а коэффициенты передачи для нижнего и верхнего участков полосы пропускания равны ( = = ). ).
За полосу пропускания фильтра  обычно принимают интервал частот, на границах которого модуль передаточной функции падает до уровня обычно принимают интервал частот, на границах которого модуль передаточной функции падает до уровня 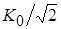 ≈ ≈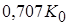 , то есть на –3 дБ. , то есть на –3 дБ.
При таком задании полосы пропускания частота среза ФНЧ и ФВЧ первого порядка совпадает с их характеристической частотой ( = = ). Близки к характеристическим и частоты среза ФНЧ и ФВЧ второго порядка, хотя в общем случае они различаются ( ). Близки к характеристическим и частоты среза ФНЧ и ФВЧ второго порядка, хотя в общем случае они различаются ( ≠ ≠ ). При ). При  > > на графиках АЧХ этих фильтров в области частоты на графиках АЧХ этих фильтров в области частоты  наблюдается «всплеск», а наблюдается «всплеск», а  > > . Полное совпадение . Полное совпадение  = = имеет место лишь при имеет место лишь при  = = . .
У ПФ характеристическая частота  соответствует частоте, на которую приходится максимум передаточной функции (для наименования такой частоты употребляются термины резонансная или квазирезонансная). Справедливы соотношения: соответствует частоте, на которую приходится максимум передаточной функции (для наименования такой частоты употребляются термины резонансная или квазирезонансная). Справедливы соотношения:
 = = ; ;  = = – – = =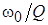 , ,
где  , ,  – нижняя и верхняя частоты среза ПФ. – нижняя и верхняя частоты среза ПФ.
Избирательные свойства фильтров в значительной мере зависят от крутизны их АЧХ в области спада. Крутизна спада  является характерным параметром фильтра и рассчитывается в децибелах на декаду является характерным параметром фильтра и рассчитывается в децибелах на декаду
 [дБ/дек]= [дБ/дек]= , ,
где  , , 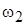 – выборочные частоты в области спада. – выборочные частоты в области спада.
Декада – практическая единица измерения частотного интервала; соответствует интервалу между частотами  и и 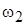 , различающимися в 10 раз ( , различающимися в 10 раз (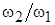 =10; =10; 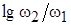 =1). =1).
Возможны реализации фильтров с использованием лишь одних пассивных элементов (пассивные фильтры). Однако в настоящее время построение фильтров часто проводится с применением активных элементов (активные фильтры), в частности, операционных усилителей (ОУ). Если подобный активный фильтр из пассивных элементов содержит только емкостные и резистивные элементы, то его называют активным RC
–фильтром.
Активные RC
–фильтры не содержат катушек индуктивности. Индуктивные катушки – это громоздкие элементы (особенно предназначенные для работы при низких частотах). Их микроэлектронное исполнение весьма затруднительно. Кроме того, в низкочастотном диапазоне катушки индуктивности имеют невысокую добротность.
Активные фильтры выгодно отличаются от пассивных еще и тем, что имеется возможность обеспечения их высокого входного и малого выходного сопротивлений. Это облегчает согласование фильтров при их соединениях между собой (имеет место независимость АЧХ промежуточных звеньев).
При проектировании сложных фильтров на основе фильтров первого и второго порядков используются различные комбинации последних. Например, применяется каскадное соединение – выход предыдущего фильтра соединяется со входом последующего. Каскадное соединение звеньев первого и второго порядков позволяет создать фильтр любого порядка. В этом случае передаточная функция фильтра равна произведению передаточных функций входящих в его состав элементарных звеньев:
 = =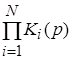 . .
Каскадное проектирование является самым распространенным методом создания активных фильтров.
1. Расчет операторной передаточной функции активного четырехполюсника
На основании исходной схемы четырехполюсника составим операторную схему замещения (рис. 3). Для этого пассивные элементы в исходной схеме заменим пассивными двухполюсниками с соответствующими операторными сопротивлениями (резистивному элементу с сопротивлением  соответствует двухполюсник с операторным сопротивлением соответствует двухполюсник с операторным сопротивлением 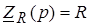 , емкостному с емкостью , емкостному с емкостью 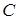 – двухполюсник с операторным сопротивлением – двухполюсник с операторным сопротивлением  ). ).

Рис.3. Схема замещения фильтра
Осуществим расчет методом узловых напряжений. Проведем топологический анализ схемы, в ходе которого выявим и пронумеруем узлы. Узел, помеченный знаком общей шины, обозначим как нулевой (узел 0) и примем его за базисный узел. Для операторных изображений узловых напряжений узлов 1–4 введем обозначения  – – . При этом отметим, что . При этом отметим, что  = =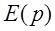 , ,  = = . Запишем систему уравнений: . Запишем систему уравнений:
U11(g1+g2+pC1)-U22pC1-U44g2=Eg1
-U11pC1+U22(g3+pC1+pC2)=0
U33(g4+g5)-U44g5=0
U44=k(U22-U33)
При  имеем U22=U33 имеем U22=U33
U11(g1+g2+pC1)-U22pC1-U44g2=Eg1
-U11pC1+U22(g3+pC1+pC2)=0
U22(g4+g5)-U44g5=0
В матричной форме система узловых уравнений примет вид

Из этой системы линейных уравнений по правилу Крамера могут быть определены операторное изображение узлового напряжения выхода четырехполюсника:
 = = , ,

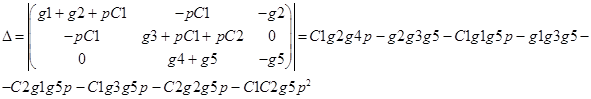
Операторная функция передачи рассматриваемого активного четырехполюсника будет равна
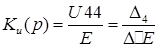
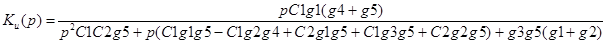
 в виде дробно-рациональной функции: в виде дробно-рациональной функции:

| где |
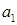 =С1g1(g4+g5) =С1g1(g4+g5) |
 =g3g5(g1+g2) =g3g5(g1+g2) |
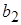 =C1C2g5 =C1C2g5 |
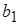 =C1g1g5-C1g2g4+C2g1g5+C1g3g5+C2g2g5 =C1g1g5-C1g2g4+C2g1g5+C1g3g5+C2g2g5 |
2.
Параметрический синтез фильтра
Сравним между собой две употребляемые формы записи передаточной функции  ПФ второго порядка (см. табл. 1, формы 1, 2), ПФ второго порядка (см. табл. 1, формы 1, 2),
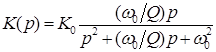 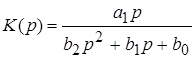
можно видеть, что
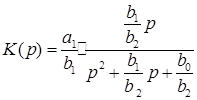
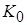 = =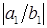 , , 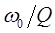 =b1/b2, =b1/b2, 
в результате получаем 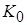 = =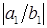 ; ;  = = = = ; ;  = = . .
Таким образом, для определения параметров (параметрического синтеза) семи пассивных элементов (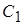 , , 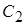 , , 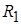 – – ) заданной цепи, удовлетворяющей заданным электрическим свойствам, имеем три уравнения. Недостающие уравнения получим, наложив следующие дополнительные условия. Исходя из сокращения номенклатуры номиналов элементов и в целях обеспечения относительно большого входного сопротивления каскадов положим ) заданной цепи, удовлетворяющей заданным электрическим свойствам, имеем три уравнения. Недостающие уравнения получим, наложив следующие дополнительные условия. Исходя из сокращения номенклатуры номиналов элементов и в целях обеспечения относительно большого входного сопротивления каскадов положим 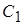 = =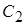 = =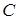 =10нФ, =10нФ, 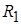 = =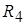 = = =1000 Ом. =1000 Ом.
Воспользуемся полученными в пункте 1 выражениями для коэффициентов  , ,  дробно-рационального представления передаточной функции дробно-рационального представления передаточной функции  через параметры элементов схемы через параметры элементов схемы 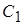 , , 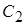 , , 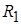 – – . В результате подстановки получим . В результате подстановки получим
 

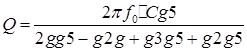
Отсюда находим
 R5= R5=
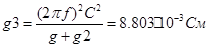 R3=114 ОМ R3=114 ОМ

Параметры всех элементов фильтра определены. Их конкретные значения выбраны в соответствии с рядами номинальных значений сопротивлений резисторов и емкостей конденсаторов.
Численные значения коэффициентов дробно-рационального представления передаточной функции  = =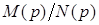 рассчитанного ФНЧ равны: рассчитанного ФНЧ равны:
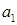 =1.013∙10-1
4
; =1.013∙10-1
4
; |
 =1.277∙10-
10 =1.277∙10-
10
|
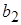 =1.299∙10-
21
; =1.299∙10-
21
; |
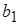 =2.099∙10-1
6
; =2.099∙10-1
6
; |
Нули 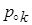 и полюсы и полюсы  фильтра определим из уравнений фильтра определим из уравнений
M(p0
)=1.013∙10-1
4
p0
=0
N(p*
)=1.299∙10-
21
p*
2
+2.099∙10-1
6
p*
+1.277 ∙10-
10
=0
Получаем, что фильтр имеет один нуль и два комплексно-сопряженных полюса:  =0 рад/с; =0 рад/с;  =-80792±ј∙302950рад/с. =-80792±ј∙302950рад/с.
Графическое изображение расположения нулей и полюсов функции на плоскости операторной переменной р=α+jwназывается диаграммой или картой нулей и полюсов
Полюсно–нулевая карта, построенная по этим данным, представлена на рис.4.

3.
Расчет частотных характеристик фильтра
Уравнение комплексной передаточной функции  может быть получено из уравнения операторной передаточной функции может быть получено из уравнения операторной передаточной функции  при замене операторной переменной при замене операторной переменной  на мнимую частоту на мнимую частоту 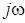 : :
 = =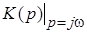 . .
В свою очередь, после выделения действительных 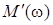 , , 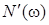 и мнимых и мнимых  , , 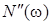 составляющих числителя составляющих числителя 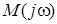 и знаменателя и знаменателя  дробного выражения комплексной передаточной функции дробного выражения комплексной передаточной функции
 = = = =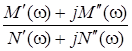 , ,
легко находятся уравнения АЧХ и ФЧХ цепи:
 = =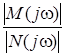 = = ; ;
 = = = = - -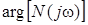 ; ;
 = = при при  ; ;
 = =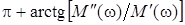 при при  , ,  ; ;
 = =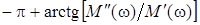 при при  , , 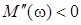 ; ;
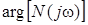 = = при при 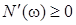 ; ;
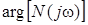 = = при при  , , 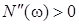 ; ;
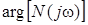 = =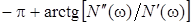 при при  , ,  . .
Уравнения АЧХ и ФЧХ фильтра получим из дробно-рационального выражения его операторной функции передачи:
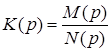 = =
Положив  = =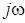 , получим выражение для комплексной передаточной функции: , получим выражение для комплексной передаточной функции:
 = = = = = =
=
Определив модуль этого комплексного выражения, найдем уравнение АЧХ фильтра:
 = =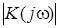 = =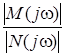 = =
Для нахождения уравнения ФЧХ нужно найти аргумент функции  : :
 = = = = = = - -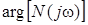 . .
Оставаясь действительным, полином числителя
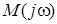 = =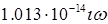
при любой частоте не меняет свой знак. Поэтому  =0 при любой =0 при любой ( (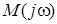 ≥0). ≥0).
У полинома знаменателя
 = = 
действительная часть
 = =
при частоте ω>313538 рад\с меняет знак. В зависимости от знака действительной части аргумент комплексной функции будет определяться по разным формулам:
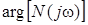 = =
при 0≤ <313538 рад/с ( <313538 рад/с ( >0); >0);
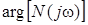 = = 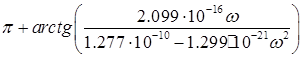
при  ≥313538 рад/с ( ≥313538 рад/с ( <0). <0).
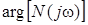 = =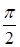
при  =313538 рад/с =313538 рад/с
Таким образом, уравнение ФЧХ будет выглядеть следующим образом
 =- =-
при 0≤ <313538рад/с <313538рад/с
 = =
при  >313538рад/с >313538рад/с
 = =
при  =313538 рад/с =313538 рад/с
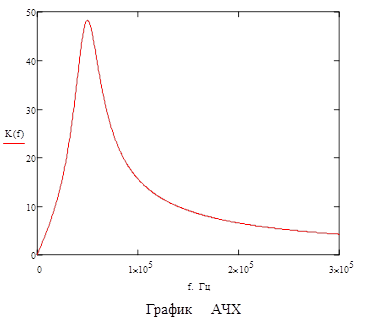
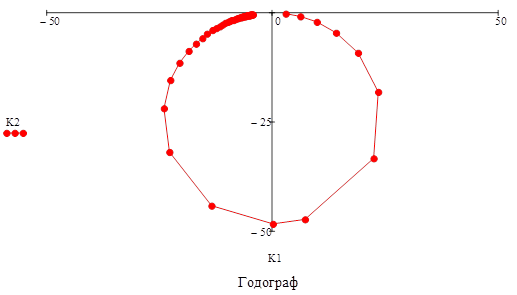
По полученным уравнениям (задавая с определенным шагом значения  и вычисляя соответствующие значения и вычисляя соответствующие значения  =2π =2π ) можно построить графики АЧХ ) можно построить графики АЧХ  и ФЧХ и ФЧХ  фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU
(jf)=K(ω)ехр(jφ(f)),а алгебраической КU
(jf)=A(f)+jB(f)=K(f)cosφ(f) + jK(f)sinφ(f). фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU
(jf)=K(ω)ехр(jφ(f)),а алгебраической КU
(jf)=A(f)+jB(f)=K(f)cosφ(f) + jK(f)sinφ(f).
По графику определим частоту среза 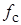 полосу пропускания полосу пропускания 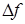 , крутизну спада амплитудно-частотной характеристики , крутизну спада амплитудно-частотной характеристики  : :
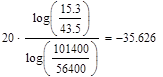 
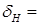 Дб/дек Дб/дек  Дб/дек Дб/дек
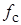 н
=39300 Гц н
=39300 Гц
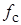 н
=63300Гц н
=63300Гц
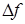 →63300-39300=24000Гц →63300-39300=24000Гц
Расчет частотных характеристик всегда проводятв определенном диапазоне частот, вкотором проявляются основные частотные свойства электрической цепи. Величину диапазона частот можно определить по полюсно-нулевой карте операторной функции.
В качестве нижней граничной частоты fн
можно принять значение, близкое к величине

где Smin
– расстояние от начала координат до ближайшей особой точки (нуля или полюса)
Это расстояние определяется как модуль особой точки: S =p0
или S=p*
.
За верхнюю граничную частоту fв
можно взять значение
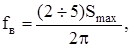
где Smax
– расстояние от начала координат до самой удаленной особой точки. Рассчитаем граничные частоты для нашего примера.
p0
=0 рад/c, 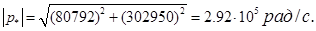
Следовательно, Smin
=p0
, Smax
=p*
,

4.
Расчет переходной характеристики фильтра
По формуле  = = найдем операторное изображение переходной характеристики найдем операторное изображение переходной характеристики  фильтра. Используя выражение для операторной передаточной функции фильтра. Используя выражение для операторной передаточной функции  из пункта 3, запишем из пункта 3, запишем
 = = = =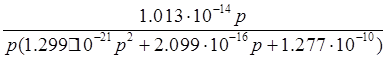
Определение оригинала переходной характеристики 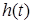 по данному изображению по данному изображению  осуществим по теореме разложения. Для этого вычислим корни уравнения осуществим по теореме разложения. Для этого вычислим корни уравнения
 = = =0, =0,
которые являются полюсами операторной функции  . Она имеет два комплексно-сопряженных полюса: . Она имеет два комплексно-сопряженных полюса:
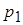 =– 80792+ј∙302950 ; =– 80792+ј∙302950 ;  = – 80792-ј∙302950 рад/с. = – 80792-ј∙302950 рад/с.
Воспользуемся формулой теоремы разложения для случая трех простых (некратных) полюсов, один из которых нулевой:
 = =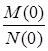 + + + + . .
 h(t)= h(t)=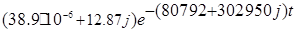 + + + +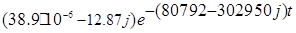
 Проведя преобразования, получим искомое уравнение переходной характеристики фильтра: Проведя преобразования, получим искомое уравнение переходной характеристики фильтра:
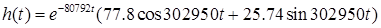
В ходе преобразований при подобных вычислениях полезно помнить формулы
 ; ; 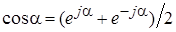 ; ;
Расчет переходной характеристики проводят в определенном временном интервале
и с определенным шагом изменения времени, которые зависит от вида функции, составляющих переходную характеристику.
Временной интервал 0 ÷ T1
определяется показателем экспоненты s и принимается примерно равным
T1
= (4 ÷ 5)/s=
Шаг изменения времени T2
можно оценить по периоду T гармонического колебания
T = 2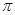 /w =6.28/302950=2,074∙ /w =6.28/302950=2,074∙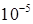 с. с.
Если принять 10 точек на период T, то шаг изменения времени T2
будет равным


5.
Анализ полученных результатов
В случае 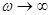 конфигурация цепи упрощается, т.к. емкостные сопротивления стремятся к нулю и емкостные элементы следует закоротить. конфигурация цепи упрощается, т.к. емкостные сопротивления стремятся к нулю и емкостные элементы следует закоротить.
Рассмотрим уравнения АЧХ и ФЧХ при условии:
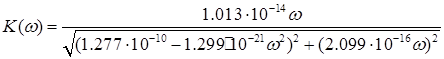
а)  =- =-
при 0≤ <313538рад/с <313538рад/с
б)  = =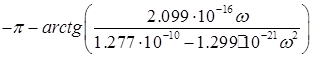
при  >313538рад/с >313538рад/с
в)  = =
при  =313538 рад/с =313538 рад/с
так как у нас  , то для ФЧХ будем применять формулу б). , то для ФЧХ будем применять формулу б).
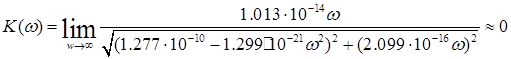

В случае 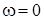 (режим постоянного тока) конфигурация цепи упрощается, так как постоянный ток не протекает через емкостные элементы. Поэтому для определения передаточной функции на постоянном токе емкостные элементы следует заменить разрывом цепи. (режим постоянного тока) конфигурация цепи упрощается, так как постоянный ток не протекает через емкостные элементы. Поэтому для определения передаточной функции на постоянном токе емкостные элементы следует заменить разрывом цепи.

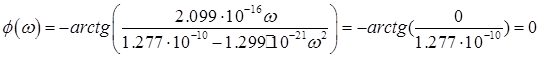
При w=313538 рад/с имеем
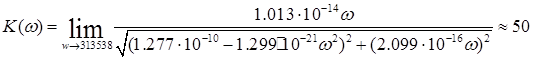
 = =
Список использованной литературы
1. Расчёт линейных активных RC-цепей: Методические указания к выполнению курсового проекта по курсу «Теоретические основы электротехники». Старцев С.А. –КГЭУ, Казань, 24с.
2. Расчет частотных и переходных характеристик линейных активных цепей: методическое пособие по курсовой работе. В.А. Михайлов, Э.И. Султанов. Казан. гос. техн. ун-т. Казань, 2001, 27 с.
3.Основыпромышленной электроники/Под ред. В. Г. Герасимова. М.: Высшая школа, 1986.
|