| ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Курсовая работа
по дисциплине «Статистика»
на тему:
«Метод средних величин
в изучении общественных явлений»
Выполнила студентка III курса
учетно-статистического факультета
специальности бухучет, анализ и аудит
***
№ зачетной книжки ***
Проверила Лаптева И.П.
Киров
2004
ОГЛАВЛЕНИЕ
Введение.. 3
Теоретическая часть.. 4
Расчетная часть.. 14
Аналитическая часть.. 19
Заключение.. 26
Список используемой литературы... 29
Введение
В данной работе рассмотрим такое понятие, как средние величины. Большое распространение в статистике коммерческой деятельности имеют средние величины. В средних величинах отображаются важнейшие показатели товарооборота, товарных запасов, цен. Средними величинами характеризуются качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др. Правильное понимания сущности средней определяет ее особую значимость в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития.
В теоретической части рассмотрим виды средних величин, а именно: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая и структурные средние - в экономическом анализе, а также условия их применения. Материал изложен с пояснениями и примерами.
В расчетной части представлены задачи на нахождение средних величин, на примере этих задач покажем различные способы нахождения средних величин, и использование их в экономическом анализе.
В аналитической части проведем небольшое исследование в области дифференциации заработной платы с использованием средних величин.
Средняя величина – важнейший вид обобщающих показателей, имеющий широкое практическое использование.
В изучении общественных явлений, социально-экономических исследованиях средняя величина является наиболее распространенной формой.
Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средняя величина отражает величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Средние величины характеризуют однотипные общественные явления по одному количественному признаку.
Средние величины используют при прогнозировании экономических и социальных показателей, составлении бизнес-планов, анализе реализации прогнозов, динамики, структуры, в расчетах экономической эффективности.
Средние величины применяют в практике учреждений банков, например, определяют средние остатки денежных средств на расчетных счетах предприятий, средние остатки просроченных ссуд, среднюю оборачиваемость кредитов.
В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.
Например, обобщающим показателем доходов рабочих акционерного общества служит средний доход одного рабочего, определяемый отношением фонда заработной платы и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих акционерного общества.
Одной из задач органов государственной статистики является характеристика уровня жизни населения в целом, а также уровня его доходов в разрезе различных социальных групп.
Уровень жизни включает большое число единиц, поэтому сравнение индивидуальных доходов каждой семьи рабочего, служащего, студента, банкира и т.д. является абсолютно невозможным. Сравнение суммарных доходов отдельных социальных групп не представляет особого интереса, так как эти группы существенно различаются по численности.
Например, численность рабочих и численность людей, занятых в сфере предпринимательства. В таких случаях используется средние показатели, средние величины доходов, доходов в расчете на одного человека или на одну семью по каждой социальной группе.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значение признака отдельных единиц совокупности могут колебаться в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, доходы такой социальной группы, как студенты государственных вузов определяется действующим положением о начислении стипендий. В то же время доходы отдельно взятого студента могут быть и очень большими (например, студент работает на хорошо оплачиваемой работе) и могут совсем отсутствовать (например, при нахождении в академическом отпуске). Сущность средних в том и заключается, что в них взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней величине отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
В каждом явлении и его развитии имеет место сочетании случайности и закономерности. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от искусственных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайных отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупности.
Там, где возникает потребность обобщения расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях.
Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и пространстве.
Средняя – это свободная характеристика закономерностей процесса в тех условиях, в которых он протекает.
Анализ средних выявляет, например, закономерности изменения производительности труда, заработной платы рабочих отдельного предприятия на определенном этапе его экономического развития, изменения климата в конкретном пункте земного шара на основе многолетних наблюдений средней температуры и т.д.
Для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних.
Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания ее типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений, исчисляется система средних показателей. Например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности труда, степенью механизации и автоматизации работ и т.д.
Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе научного способа расчета.
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая;
- средняя кубическая и т.д.
Средняя арифметическая рассчитывается в двух формах – простой и взвешенной. Исходной, определяющей формой служит простая средняя.
Средняя арифметическая простая применяется в тех случаях, когда известны только отдельные значения признака (варианты).
Чтобы исчислить среднюю арифметическую нужно сумму всех значений признаков разделить на их число. Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений.
    
где х1
, х2
, …, хn
– индивидуальные значения варьирующего признака, n – число единиц совокупности.
Средняя из вариантов, которые повторяются различное число раз, или имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности.
Средняя арифметическая взвешенная – средняя сгруппировочных величин вычисляется по формуле

где f1
, f2
, …, fn
– веса (частоты повторения признаков),
 – сумма произведений величины признаков на их частоты, – сумма произведений величины признаков на их частоты,
 – общая численность единиц совокупности. – общая численность единиц совокупности.
Например:
Вклады населения в 2000 году характеризуются следующими данными (млрд. руб.):
Таблица 1. Информация о вкладах населения в 2000 году
| 1 полугодие
|
| Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
Июнь
|
| 76007,3
|
84347,0
|
89694,6
|
93653,
|
96062,
|
97933,7
|
| 2 полугодие
|
| 1.07
|
1.08
|
1.09
|
1.10
|
1.11
|
1.12
|
1.01
|
| 99203,5
|
104396,8
|
108565,2
|
111522,5
|
114864,8
|
116404,5
|
118244,8
|
Рассчитать среднемесячную сумму вкладов населения в первом и втором полугодии.
Для расчета среднемесячной суммы вкладов населения в первом полугодии используем формулу средней арифметической простой.


Для расчета среднемесячной суммы вкладов населения во втором полугодии применим формулу средней хронологической

 
Вывод. Среднемесячные суммы вкладов в первом и втором полугодиях рассчитываются по разным формулам.
В первом полугодии по средней арифметической простой, так как данный ряд динамики интервальный.
Во втором полугодии среднемесячная сумма вкладов рассчитывается по средней хронологической, так как этот ряд динамики моментный.
Средняя арифметическая взвешенная рассчитывается в тех случаях, когда связь между признаками прямая, т.е. при умножении одного признака (х) на другой (f). Получают третий признак, имеющий реальный экономический смысл. Например, если при определении средней заработной платы известны заработная плата одного рабочего и численность рабочих, определяемый фонд заработной платы (х*f).

Если связь между признаками обратная, то нужно делить один показатель (объемный – w) на другой (х), используют формулу средней гармонической
 , где х – варианты, w – объем признака , где х – варианты, w – объем признака
Например, если дан фонд заработной платы (w) и заработная плата рабочего (х), то путем деления первого показателя на второй находят численность рабочих  . .
Например, заработная плата работников предприятия за год составила:
Таблица 2. Информация о заработной плате работников за год
| Номер чеха
|
Средняя заработная плата работника,
тыс. руб. (х)
|
Число работников
(f)
|
Фонд заработной платы
(x*f)
|
| 1
2
3
|
62
70
58
|
180
200
120
|
11160
14000
6960
|
| Всего
|
190
|
500
|
32120
|
Определить среднегодовую заработную плату работника предприятия.

 тыс. руб. тыс. руб.
Для определения среднегодовой заработной платы использована формула средней арифметической взвешенной.
Например:
Рассчитать среднюю заработную плату одного рабочего по трем цехам предприятия.
Таблица 3. Информация о заработной плате работников по цехам
| Номер чеха
|
Средняя заработная плата рабочего,
(х)
|
Число работников, чел.

|
Фонд заработной платы, руб.
(w)
|
| 1
2
3
|
50
62
70
|
80
120
100
|
4000
7440
7000
|
| Всего
|
300
|
18440
|
В данной задаче имеется такой показатель, как фонд заработной платы, который является объемным, следовательно, задача решается по средней гармонической взвешенной.

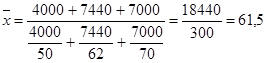 тыс. руб. тыс. руб.
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной, которая имеет формулу  . .
Средняя квадратическая простая применяется средней величины стороны n квадратных участков.
Например:
Имеются три участка земельной площади со сторонами квадрата
х1
= 200 м
х2
= 100 м
х3
= 300 м

 м м
 - средняя квадратическая невзвешенная - средняя квадратическая невзвешенная
 - средняя кубическая взвешенная - средняя кубическая взвешенная
 - средняя геометрическая - средняя геометрическая
Основное применение средняя геометрическая находит при определении средних темпов роста.
Например:
Стоимость потребительской корзины за год в результате инфляции возросла в 6 раз. Каков среднемесячный темп инфляции?
 ; ;
 или 116 %. или 116 %.
Среднемесячный темп инфляции составляет 16 %.
Например:
За 1 год объем производства вырос на 20 %, а за 2 год снизился на 20 %. Определить средний тем роста производства за 2 года.
1 год – 120 % (100+20)
2 год – 80 % (100-20)


Т.е. темп роста за 2 года снизился на 2,02 % (100-97,98).
1. По первичным данным таблицы 5 (в методическом указании 5.5) определите средний размер розничного товарооборота в расчете на одно предприятие торговли. Укажите вид средней.
2. Постройте статистический ряд распределения торговых предприятий по размеру товарооборота, образовав пять групп с равными интервалами, охарактеризовав их числом предприятий и удельным весом предприятий. По ряду распределения рассчитайте средний размер розничного товарооборота на одно торговое предприятие, взвешивая значение варьирующего признака:
а) по числу предприятий;
б) по удельному весу предприятий.
Сравните полученную среднюю с п.1 и поясните их расхождение.
3. За отчетный год имеются данные о кредитных операциях банков:
Таблица 4. Данные о кредитных операциях банков
| Вид кредита
|
Банк 1
|
Банк 2
|
| Годовая процентная ставка
|
Сумма кредита, млн. руб.
|
Годовая процентная ставка
|
Доход банка, млн. руб.
|
| Краткосрочный
Долгосрочный
|
20
16
|
500
150
|
21
15
|
126
30
|
Определите среднюю процентную ставку кредита:
а) по каждому банку;
б) по двум банкам.
Таблица 5. Розничный товарооборот и издержки обращения предприятий
| № п/п
|
Розничный товарооборот
|
Издержки обращения
|
| А
|
1
|
2
|
| 1
|
510
|
30
|
| 2
|
560
|
33
|
| 3
|
800
|
46
|
| 4
|
465
|
31
|
| 5
|
225
|
16
|
| 6
|
390
|
25
|
| 7
|
640
|
39
|
| 8
|
405
|
26
|
| 9
|
200
|
15
|
| 10
|
425
|
34
|
| 11
|
570
|
37
|
| 12
|
472
|
28
|
| 13
|
250
|
19
|
| 14
|
665
|
38
|
| 15
|
650
|
36
|
| 16
|
620
|
35
|
| 17
|
380
|
24
|
| 18
|
550
|
38
|
| 19
|
750
|
44
|
| 20
|
660
|
36
|
| 21
|
450
|
27
|
| 22
|
563
|
34
|
| 23
|
400
|
26
|
| 24
|
553
|
38
|
| 25
|
772
|
45
|
Решение:
1. Для определения среднего размера розничного товарооборота в расчете на одно предприятие торговли воспользуемся формулой средней арифметической взвешенной
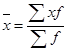
 =(510*30+560*33+800*46+465*31+225*16+390*25+640*39++405*26+200*15+425*34+570*37+472*28+250*19+665*38+ +650*36+620*35+380*24+550*38+750*44+660*36+450*27+ +563*34+400*26+553*38+772*45):(30+33+46+31+16+25+39+ +26+15+34+37+28+19+38+36+35+24+38+44+36+27+34+26+ +38+45) = 444937: 800 =556,2 =(510*30+560*33+800*46+465*31+225*16+390*25+640*39++405*26+200*15+425*34+570*37+472*28+250*19+665*38+ +650*36+620*35+380*24+550*38+750*44+660*36+450*27+ +563*34+400*26+553*38+772*45):(30+33+46+31+16+25+39+ +26+15+34+37+28+19+38+36+35+24+38+44+36+27+34+26+ +38+45) = 444937: 800 =556,2
Средний размер розничного товарооборота в расчете на одно предприятие торговли составляет 556,2 млн. руб.
2. Для построения статистического ряда распределения торговых предприятий по размеру товарооборота с выделением пяти групп найдем величину равного интервала.
Величина равного интервала определяется по формуле:  , где где xmax
и xmin
– максимальное и минимальное значение признака, n – число групп. , где где xmax
и xmin
– максимальное и минимальное значение признака, n – число групп.
В данной задаче величина интервала  . .
| 225, 200, 250
|
3
|
675
|
| 390, 405, 425, 380, 400
|
5
|
2000
|
| 465, 472, 450, 510, 553, 550
|
6
|
3000
|
| 560, 640, 570, 620, 563, 665, 650, 660
|
8
|
4928
|
| 750, 772, 800
|
3
|
2322
|
| 25
|
12925
|
Далее находим средний размер розничного товарооборота на одно торговое предприятие по числу предприятий по формуле 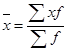
 млн.руб. млн.руб.
Находим средний размер розничного товарооборота на одно торговое предприятие по удельному весу предприятий.
 млн.руб. млн.руб.
Из данных расчетов можем составить таблицу.
Таблица 6. Интервальный ряд распределения предприятий
| Группы предприятий
|
Число предприятий в группе
|
Товарооборот
|
Удельный вес, %
|
| 200 – 320
|
3
|
675
|
5,20
|
| 320 – 440
|
5
|
2000
|
15,50
|
| 440 – 560
|
6
|
3000
|
23,20
|
| 560 – 680
|
8
|
4928
|
38,10
|
| 680 – 800
|
3
|
2322
|
18,00
|
| Всего
|
25
|
12925
|
100
|
При сравнении полученных в п.2 результатов средней с результатом, полученным в п.1 обнаруживаем небольшое расхождение, которое объясняется тем, что в первом случае расчет проводился по формуле средней арифметической взвешенной в расчете на одно предприятие, а во втором случае по формуле средней арифметической взвешенной по ряду распределения предприятий по размеру товарооборота с выделением пяти групп (интервалов). При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы.
3. а) Для определения средней процентной ставки по банку № 1 применим формулу средней арифметической взвешенной  . .
 или 19 % годовых или 19 % годовых
Для определения средней процентной ставки по банку № 2 используем формулу средней гармонической, так как в задании указан доход банка

 , т.е. 19,5 % годовых. , т.е. 19,5 % годовых.
б) Средняя процентная ставка по двум банкам определяется по средней арифметической простой

 , т.е. 18 % годовых по обоим видам кредитов. , т.е. 18 % годовых по обоим видам кредитов.
В данной части курсовой работы проведены аналитические исследования в области дифференциации заработной платы с использованием средних величин, на примере Кировской области. Все используемые данные взяты за 2004г.
На начало 2004 г. в области насчитывалось 33,9 тыс. крупных и средних предприятий, представивших данные о заработной плате, которая в мае в среднем составила 4358,3 руб. На этих предприятиях работало 433855 человек.
Данные статистических наблюдений сообщают информацию только о средней по отраслям экономики заработной плате. Однако если взвесить среднюю заработную плату на численность работающих, то есть условно распространить среднюю зарплату по отрасли на каждого, работающего в данной сфере, то можно проследить дифференциацию оплаты труда.
Номинальная начисленная средняя заработная плата в мае 2004 года в целом по области (включая предприятия и организации малого предпринимательства) составила 4358,3 рубля.
Динамика начисленной номинальной и реальной средней заработной платы в расчете на одного работника характеризуется следующими данными:
Таблица 7. Средняя номинальная и средняя реальная заработная плата в расчете на одного работника
| Средняя номиналь-ная заработная плата, рублей
|
В процентах к
|
Реальная заработная плата в процентах к
|
| преды-дущему месяцу
|
соответствующему периоду предыдущего года
|
преды-дущему месяцу
|
соответствующему периоду предыдуще-го года
|
| 2003
|
| Январь
|
3137,4
|
83,9
|
120,3
|
82,1
|
105,8
|
| Февраль
|
3142,6
|
100,0
|
122,0
|
98,6
|
106,6
|
| Март
|
3413,4
|
108,6
|
121,0
|
108,0
|
106,0
|
| Январь - март
|
3233,2
|
…
|
121,2
|
…
|
106,2
|
| Апрель
|
3416,1
|
100,1
|
119,4
|
99,3
|
105,0
|
| Май
|
3441,3
|
100,8
|
118,6
|
100,5
|
105,7
|
| Июнь
|
3648,4
|
106,1
|
117,4
|
104,5
|
104,1
|
| Январь - июнь
|
3365,6
|
...
|
119,7
|
...
|
105,5
|
| Июль
|
3727,7
|
102,2
|
114,9
|
101,2
|
101,8
|
| Август
|
3630,3
|
97,5
|
114,4
|
97,3
|
101,4
|
| Сентябрь
|
3701,8
|
102,0
|
114,0
|
101,4
|
100,5
|
| Январь - сентябрь
|
3470,4
|
...
|
117,7
|
....
|
103,9
|
| Октябрь
|
3975,3
|
107,1
|
122,3
|
105,0
|
107,1
|
| Ноябрь
|
4006,8
|
100,8
|
124,4
|
99,9
|
109,3
|
| Декабрь
|
4847,1
|
121,0
|
129,0
|
119,8
|
113,9
|
| Январь – декабр
|
3668,4
|
...
|
119,8
|
...
|
105,6
|
| 2004
|
| Январь
|
4012,5
|
82,5
|
123,7
|
81,6
|
110,5
|
| Февраль
|
4150,6
|
103,6
|
131,1
|
102,7
|
117,7
|
| Март
|
4417,2
|
106,3
|
128,7
|
105,2
|
115,0
|
| Январь - март
|
4192,6
|
...
|
127,8
|
...
|
114,4
|
| Апрель
|
4423,8
|
100,1
|
128,6
|
99,4
|
115,1
|
| Май
|
4358,3
|
98,6
|
125,9
|
97,8
|
112,0
|
| Январь - май
|
4270,7
|
...
|
127,5
|
...
|
114,0
|

Рис.1. Темпы роста (снижения) номинальной и реальной заработной платы
Начисленная средняя заработная плата в расчете на одного работника по отраслям экономики приведены в таблице:
Таблица 8. Средняя заработная плата по отраслям экономики
| Начисленная средняя заработная плата в месяц, рублей
|
Май 2004
в % к
|
| маю 2003
|
средне-областному уровню
|
| январь - май 2004
|
май 2004
|
| Всего
|
4270,7
|
4358,3
|
125,9
|
100,0
|
| в том числе:
|
| Промышленность
|
4899,1
|
4948,7
|
128,5
|
113,5
|
| Сельское хозяйство
|
2061,8
|
2370,0
|
125,7
|
54,4
|
| Транспорт
|
6584,6
|
6805,3
|
133,5
|
156,1
|
| Связь
|
5324,0
|
5795,0
|
135,0
|
133,0
|
| Строительство
|
4236,6
|
4431,5
|
118,8
|
101,7
|
| Торговля и общественное питание
|
3206,6
|
3416,0
|
128,2
|
78,4
|
| Оптовая торговля продукцией производственно-технического назначения
|
5558,6
|
5430,7
|
121,1
|
124,6
|
| Непроизводствен-ные виды бытового обслуживания населения
|
2661,2
|
2891,1
|
94,8
|
66,3
|
| Здравоохранение, физкультура и социальное обеспечение
|
3253,4
|
3485,3
|
132,2
|
80,0
|
| Образование
|
3056,4
|
3145,4
|
132,5
|
72,2
|
| Культура и искусство
|
2607,3
|
2678,6
|
130,3
|
61,5
|
| Наука и научное
обслуживание
|
5401,0
|
5726,1
|
131,3
|
131,4
|
| Финансы, кредит,
страхование
|
10542,3
|
8905,4
|
91,8
|
в 2,0р
|
| Управление
|
6328,7
|
6185,3
|
121,6
|
141,9
|
| Общественные
организации
|
4037,0
|
4218,2
|
121,0
|
96,8
|
Таблица 9. Распределение работающих по уровню заработной платы
| Численность работающих, (человек)
|
В к общей численности работающих
|
Кумулятивный (накапливаемый процент)
|
| Всего работающих:
|
433855
|
100,0
|
| В том числе с уровнем средней заработной платы на предприятии рублей:
до 1000
|
| 1000-2000
|
| 2000-3000
|
71472
|
16,5
|
16,5
|
| 3000-4000
|
146036
|
33,7
|
50,2
|
| 4000-5000
|
143856
|
33,1
|
83,3
|
| 5000-6000
|
16455
|
3,8
|
87,1
|
| 6000-8000
|
47840
|
11,0
|
98,1
|
| 8000-10000
|
8196
|
1,9
|
100
|
| Свыше 10000
|

Рис. 2. Отклонение средней заработной платы по отраслям экономики от среднего уровня по области в мае 2004 года
В мае 2004 года уровень начисленной средней заработной платы работников здравоохранения, образования, культуры и искусства относительно средней зарплаты в промышленности составил соответственно - 74,0, 63,6 и 54,1 процента.
Территориальная дифференциация заработной платы обусловлена отраслевой структурой экономики районов. В среднем за май 2004 года наиболее высокий ее уровень (относительно среднеобластного) на крупных и средних предприятиях и организациях сложился в Кирово-Чепецком районе (выше в 1,2 раза), самый низкий - в Пижанском, Малмыжском, Богородском, Кильмезском, Лебяжском, Немском и Тужинском районах (ниже в 2,2 - 2,0 раза). Средняя заработная плата на крупных и средних предприятиях города Кирова составила 5738,3 рубля, что выше среднеобластного значения на 30,7 процента.
Итак, в области наблюдается существенная дифференциация уровней заработной платы, что отражает процесс расслоения общества по величине доходов. Применяемое в статистической практике среднее, вычисляемое без проверки характера распределения данных, испытывает влияние экстремальных значений и может искажать явления, происходящие в обществе. Значимость этого вывода имеет особую важность для показателей, характеризующих уровень жизни.
В заключении подведем итоги. Средние величины — это обобщающие показатели, в которых находят выражения действие общих условий, закономерность изучаемого явления. Статистические средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения (сплошного или выборочного). Однако статистическая средняя будет объективна и типична, если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений). Применение средних должно исходить из диалектического понимания категорий общего и индивидуального, массового и единичного.
Средняя отражает то общее, что складывается в каждом отдельном, единичном объекте благодаря этому средняя получает большое значение для выявления закономерностей присущих массовым общественным явлениям и незаметных в единичных явлениях.
Отклонение индивидуального от общего — проявление процесса развития. В отдельных единичных случаях могут быть заложены элементы нового, передового. В этом случае именно конкретных фактор, взятые на фоне средних величин, характеризует процесс развития. Поэтому в средней и отражается характерный, типичный, реальный уровень изучаемых явлений. Характеристики этих уровней и их изменений во времени и в пространстве являются одной из главных задач средних величин. Так, через средние проявляется, например, свойственная предприятиям на определенном этапе экономического развития; изменение благосостояния населения находит свое отражение в средних показателях заработной платы, доходов семьи в целом и по отдельным социальным группам, уровня потребления продуктов, товаров и услуг.
Средний показатель — это значение типичное (обычное, нормальное, сложившееся в целом), но таковым оно является по тому, что формируется в нормальных, естественных условиях существования конкретного массового явления, рассматриваемого в целом. Средняя отображает объективное свойство явления. В действительности часто существует только отклоняющиеся явления, и средняя как явления может и не существовать, хотя понятие типичности явления и заимствуется из действительности. Средняя величина является отражения значения изучаемого признака и, следовательно, измеряется в той же размеренности что и этот признак. Однако существуют различные способы приближенного определения уровня распределения численности для сравнения сводных признаков, непосредственно не сравнимых между собой, например средняя численность населения по отношению к территории (средняя плотность населения). В зависимости от того, какой именно фактор нужно элиминировать, будет находиться и содержание средней.
Сочетание общих средних с групповыми средними дает возможность ограничить качественно однородные совокупности. Расчленяя массу объектов, составляющих то или иное сложное явления, на внутренне однородные, но качественно различные группы, характеризуя каждую из групп своей средней, можно вскрыть резервы процесс нарождающегося нового качества. Например, распределения населения по доходу позволяет выявить формирование новых социальных групп. В аналитической части мы рассмотрели частный пример использования средней величины. Подводя итог можно сказать, что область применения и использования средних величин в статистике довольно широка.
1. Гусаров В.М. Статистика: Учебн. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 463 с.
2. Гусаров В.М. Теория статистики: Учебн. пособие для вузов. – М.:Аудит, ЮНИТИ,1998. – 247 с.
3. Социально-экономическая статистика: Учебник для вузов /Под ред. проф. Б.И. Башкатова. – М.: ЮНИТИ-ДАНА, 2002. – 703 с.
4. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / А.И. Харламов, О.Э.Башина, В.Т. Бабурин и др.; Под ред. А.А. Спирина, О.Э.Башиной. – М.: Финансы и статистика, 1994. – 296 с.
5. Практикум по статистике: Учеб. пособие для вузов / Под ред. В.М.Симчеры /ВЗФЭИ. – М.: ЗАО «Финстатинформ», 1999. – 259с.
6. Российский статистический ежегодник: стат. Сб./Госкомстат России. - Р76 М., 2004. - 679 стр.
7. http://www.infostat.ru/
|