ПАКЕТЫ ДЛЯ МАТЕМАТИЧЕСКИХ РАСЧЕТОВ
В настоящее время программные средства, ориентированные на решение
математических задач
(при этом, под математической
понимается любая задача, алгоритм которой может быть описан в терминах того или иного раздела математики), весьма обширны и условно могут быть дифференцированы на пять
уровней:
1. встроенные средства различной степени развития той или иной системы программирования; (системы программирования, как Basic, С, Pascal)
2. специальные языки программирования; (Fortran, Prolog)
3. узкоспециальные.( пакеты MacMath, Phaser, Eureka)
4. специальные (пакеты StatGraf, Macsyma, Dynamics, Derive)
5. общие пакеты. (MathCAD, REDUCE, MatLab
)
Наконец, современное развитие компьютерных технологий, ориентированных на создание интегрированных пакетов multimedia-
технологии
привело к появлению нового уровня математических пакетов, из которых наиболее известными являются пакеты MAPLE V
фирмы Maple
Software
Inc.
и Mathematica
фирмы Wolfram
Research
Inc.
Пакет MATHCAD как средство решения математических задач.
Общая характеристика пакета
Пакет имеет естественный
входной язык представления математических зависимостей и инструменты их набора типа предлагаемых в Microsoft Equation
Mathcad оборудован текстовым процессором, позволяющим, например, оформить статью без помощи специализированных средств.
Особенности ввода:
· Мнимая единица записывается как i или j сразу
после числового множителя.
· Углы по умолчанию задаются в радианах.
· Латинские буквы, цифры и знаки операций, включая возведение в степень
· указывающие прядок действий круглые скобки
- набираются непосредственно с клавиатуры.
Нажатие [Ctrl+G] вслед за набором латинской буквы преобразует ее в греческую.
Умножение набирается как *, деление — посредством /. В процессе ввода, знак умножения автоматически заменяется точкой, а делимое и делитель представляются как числитель и знаменатель дроби. Знак возведения в степень переводит последующее выражение в показатель степени, а открывающая квадратная скобка — в индекс. Возврат на основной уровень строки, (а также переход к набору знаменателя) выполняется нажатием [Space].
Набор \ вызывает шаблон для квадратного корня, апострофа — появление круглых скобок вокруг выделенного подвыражения, вертикальной черты — шаблон для вычисления абсолютной величины или определителя матрицы.
Присваивание переменным; числовых значений производится набором конструкции <имя>:<число> (двоеточие будет заменено знаком присваивания).
Например x:6 получаем на экране x:=6.<
Вывод результатов выполняется по нажатию клавиши [=]. Знаки равенства в условиях и уравнениях набираются только по [Ctrl+=]. Набор завершается нажатием [Enter] или щелчком мышью вне поля набора.
Интерфейс пакета MATHCAD

MathCAD работает с
документами
. С точки зрения пользователя, документ - это чистый лист бумаги, на котором можно размещать блоки трех основных типов: математические выражения, текстовые фрагменты и графические области.
Расположение нетекстовых блоков в документе имеет принципиальное значение - слева направо и сверху вниз.
Точка ввода на рабочем листе отмечается красным крестиком он называется
«визир
»
Математические выражения
К основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры.
Операторы
- элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.
К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы)
Функции
Функция - выражение, согласно которому проводятся некоторые вычисления с аргументами и определяется его числовое значение.
Следует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок.
Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции.

Главным признаком функции является возврат значения
, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.

Функции в пакете MathCAD могут быть встроенные.
Способы вставки встроенной функции
· Выбрать пункт меню Вставка / Функция.
· Нажать комбинацию клавиш Ctrl + E.
· Щелкнуть на кнопке 
Текстовые области
Текстовая область предназначена для небольших кусков текста - подписей, комментариев и т. п. Вставляется с помощью команды Вставка / Текстовая область
или комбинации клавиш Shift + "
(двойная кавычка).
Графические области
Графические области делятся на три основных типа - двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на основании обработанных данных.
Для создания декартового
графика
:
1. Установить визир в пустом месте рабочего документа.
2. Выбрать команду Вставка / График / Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку  Графики. Появится шаблон декартового графика. Графики. Появится шаблон декартового графика.
3. Введите в средней метке под осью Х первую независимую переменную, через запятую - вторую и так до 10, например х1, х2, …
4. Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую - вторую и т. д., например у1(х1), у2(х2), …, или соответствующие выражения.
5. Щелкните за пределами области графика, что бы начать его построение.
Трехмерные, или 3D-графики,
отображают функции двух переменных вида Z(X, Y).
Пример:

Решение математических задач с помощью MATHCAD
Численное решение нелинейного уравнения
Для простейших уравнений вида f
(x
) = 0 решение в Mathcad находится с помощью функции root.
root( f
(х
1, x
2, …
), х
1, a, b
)
Возвращает значение х
1
, принадлежащее отрезку [a, b
]
, при котором выражение или функция f
(х
)
обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.
Аргументы
f
(х
1, x
2, …
)
- функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
х
1 -
имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
a, b
-
необязательны, если используются, то должны быть вещественными числами, причем a
< b
.
Приближенные значения корней (начальные приближения
) могут быть:
1. Известны из физического смысла задачи.
2. Найдены графическим способом.
Наиболее распространен графический способ
определения начальных приближений. Принимая во внимание, что действительные корни уравнения f
(x
) = 0 - это точки пересечения графика функции f
(x
) с осью абсцисс, достаточно построить график функции f
(x
) и отметить точки пересечения f
(x
) с осью Ох,
или отметить на оси Ох
отрезки, содержащие по одному корню.
Пример решения нелинейного уравнения:
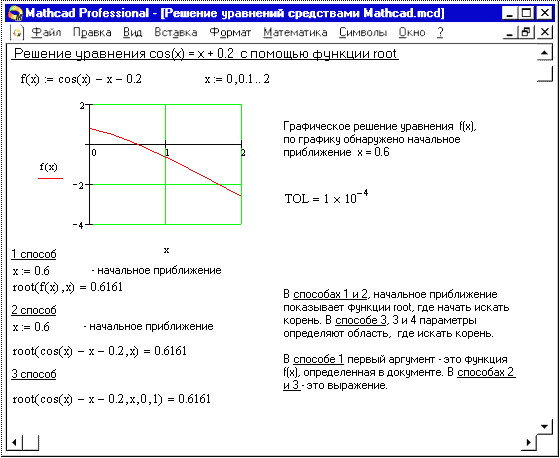
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
nx
n
+ ... + v2x
2
+ v
1x
+ v
0,
лучше использовать функцию polyroots
, нежели root.
В отличие от функции root,
функция polyroots
не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.
Polyroots(v
)
возвращает корни полинома степени n
. Коэффициенты полинома находятся в векторе v
длины n
+1. Возвращает вектор длины n
, состоящий из корней полинома.
Аргументы: v - вектор, содержащий коэффициенты полинома.
Вектор v удобно создавать использую команду Символы Þ Коэффициенты полинома.
Пример нахождения корней полинома:

Решение систем уравнений
MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.
Для решения системы уравнений необходимо выполнить следующее:
1. Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.
2. Напечатать ключевое слово Given
. Оно указывает Mathcad, что далее следует система уравнений.
3. Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >,
4. Введите любое выражение, которое включает функцию Find
, например: а:= Find(х, у)
.
Find
(z
1, z
2, . . .
)
Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
Ключевое слово Given
, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find
, называют блоком решения уравнений.
Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given
и имя функции Find
.
Пример решение системы уравнений в MathCAD.
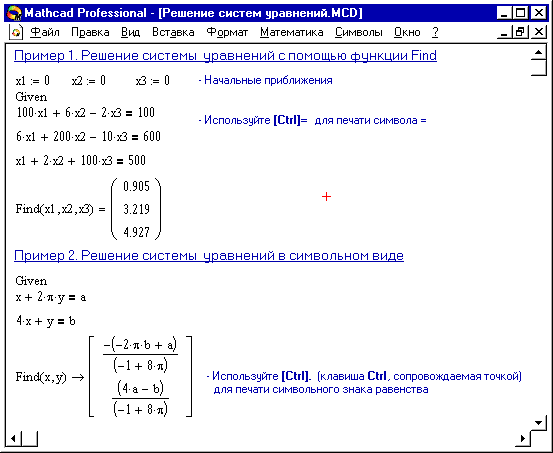
Возможности пакета MAPLE для решения математических задач.
Общая характеристика пакета
Документ системы Maple состоит из различных объектов — текстовых областей, областей ввода, графических областей, секций, подсекций и т.д. На экране дисплея в среде Maple по умолчанию строки ввода прописаны красным цветом, ответ системы - синим, комментарии пользователя - черным. В строках рабочего листа после приглашения > набираются команды состоящие главным образом ввызове ее процедур. Команды выполняются последовательно сверху вниз. Команды Maple завершаются символами :
или ;
(первый вариант подавляет вывод). Часть строки после символа. # воспринимается как комментарий.

Типы данных
Входной язык пакета Maple не предусматривает обязательного объявления типов переменных. К встроенным типам данных, относятся рациональные, вещественные (с плавающей точкой), логические и символьные.
Система имеет встроенные константы Pi, I =  . Основание натуральных логарифмов е
отсутствует, и работа с ним: заменяется ссылками на функцию ехр. В частности, собственно е
приходится представлять как ехр(1).
Бесконечность задается словом infinity. Все переменные по умолчанию считаются комплексными. . Основание натуральных логарифмов е
отсутствует, и работа с ним: заменяется ссылками на функцию ехр. В частности, собственно е
приходится представлять как ехр(1).
Бесконечность задается словом infinity. Все переменные по умолчанию считаются комплексными.
Из элементарных объектов могут быть сформированы более сложные – множества и списки. Элементы множества перечисляются через запятую в фигурных скобках и порядок их не важен, элементы списка – в [ ] и порядок важен. Обычно решения уравнений выдаются в виде списка.
Операторы обработки
Для формирования выражений используют стандартные символы +, -, *, /, ^, !.
Чтобы запомнить результаты вычислений необходимо присвоить некоторой переменной это значение. Ссылки на результаты трех предшествующих пунктов рабочего листа осуществляются с помощью знака %. Соответствующей кратности. Например:
>ex:=expand((x+l)*(x~2-x+l)); #перемножить
ex:=x^3+1
>factor(%);
#разложить на множители выражение, полученное в предыдущем пункте
(x+l)(x^2-x+l)
Примеры использования Maple для решения математических задач
Решение уравнений и систем уравнений
Используется оператор Solve(выражение, переменная)
;
Пример
:
>ex:=x^2+2*x-12;
>sol:=solve(ex,x);
>sol:=[1,-1,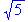 ,- ,-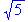 ]; ];
Если необходимо решить систему уравнений по одной или нескольким переменным данные необходимо вводить как множества - в фигурных скобках.
Эквивалентные преобразования
subs
– выполняет замену переменных во втором аргументе согласно первому.
Пример
: >
subs (x=sqrt(r), 3*x+x^2);
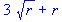
expand
- разворачивает произведения и функции сложных аргументов в суммы
Пример
:
>
expand((x+3)*(x-2));
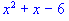
>
expand(cos(x-y));

factor
выполняет противоположные преобразования.
Пример:
> factor(x^3-1,complex);

normal
- приводит выражение к форме многочленов или дробей, числитель и знаменатель которых – взаимно простые полиномы с целыми коэффициентами.
Пример
:
> normal ((x^2-y^2)/(x-y)^3);

combine
– пытается объединить показатели степенных функций-сомножителей и понизить степени тригонометрических функций переходом к кратным углам.
Пример
:
>combine(4*sin(x)^3,trig);

>combine(exp(x)^2*exp(y),exp);

Операции математического анализа
| Операция
|
Пример команды MAPLE
|
Ответ
|
| Вычисление пределов
|
>limit(sin(x)/x, x=0);
|

1
|
| Дифференцирование
|
>diff(sin(x),x)
|

|
| Неопределенный интеграл
|
>int(sin(x),x)
|
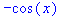
|
| Определенный интеграл
|
>int(sin(x),x=0..Pi)
|

|
Графические возможности пакета Maple
Построение двумерных и трехмерных графиков.
Используется команда
Plot
(
f,
h,
v,
options)
где
f – задаваемая функция,
h – диапазон аргумента (по умолчанию –10,10),
v – диапазон значений функции (необязателен),
options – опции, задающие вид координат, внешний вид графика и т.п.
| Построение графиков функций в декартовых
координатах
|
Построение графика в полярных
координатах
|
| > plot([sin(x), x^2/6], x=-5..5, color=[red,blue], style=[line, point]);
|
> plot (sqrt(x),x=-5..5, coords=polar);
|
| 
|

|
Столь же просто, как и график обычной функции в Декартовой системе координат, можно построить график трехмерной поверхности. В данном случае задана функция двух переменных Z(x,y):=sin(x*y) и ее график строится с использованием графической функции plot3d.

|