| Некоторые приложения определенного интеграла в математике
Курсовая работа студента гр. МТ-21
Нургалиев А.З.
Павлодарский университет
Павлодар 2005 год.
1. Введение.
В курсовой работе рассмотрены вопросы некоторого приложения определенного интеграла. Цель: изучить актуальность применения определенного интеграла и широту его использования в математике, оценить ее практическую и теоретическую значимость.
При разработки данного вопроса, был также рассмотрен несобственный интеграл, как частный случай определенного интеграла, его определение и виды.
2. Определенный интеграл.
Пусть функция f(x) задана в некотором промежутке [a,b]. Разобьем этот промежуток произвольным образом на части, вставив между a и b точки деления: 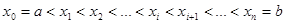 . Наибольшую из разностей . Наибольшую из разностей
 (i=0,1,2, …,n-1) будем впредь обозначать через λ. (i=0,1,2, …,n-1) будем впредь обозначать через λ.
Возьмем в каждом из частных промежутков 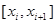 по произволу точку по произволу точку 
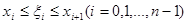
и составим сумму
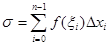 . .
Говорят, что сумма σ при λ→0 имеет (конечный) предел I, если для каждого числа ε>0 найдется такое число δ>0, что, лишь только λ<δ (т.е. основной промежуток разбит на части, с длинами 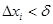 ), неравенство ), неравенство
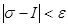
выполняется при любом выборе чисел  . .
Записывают это так:
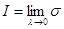 . (1) . (1)
Этому определению «на языке ε-δ», как обычно, противопоставляется определение «на языке последовательностей». Представим себе, что промежуток [α,b] последовательно разбивается на части, сначала одним способом, затем – вторым, третьим и т.д. Такую последовательность разбиений промежутка на части мы будем называть основной, если соответствующая последовательность значений 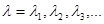 сходится к нулю. сходится к нулю.
Равенство (1) можно понимать теперь и в том смысле, что последовательность значений суммы σ, отвечающая любой основной последовательности разбиений промежутка, всегда стремится к пределу I, как бы ни выбирать при этом  . .
Второе определение позволяет перенести основные понятия и предложения теории пределов и на этот новый предел.
Конечный предел I суммы σ при λ→0 называется определенным интегралом функции f(x) в промежутке от α до b и обозначается символом
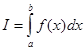 ; ;
в случае существования такого предела функции f(x) называется интегрируемой в промежутке [α,b].
Числа α и b носят название, соответственно, нижнего и верхнего пределов интеграла. При постоянных пределах определенный интеграл представляет собой постоянное число.
3. Несобственные интегралы.
Пусть f непрерывна на луче на луче 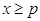 и F(x) – первообразная для f на луче и F(x) – первообразная для f на луче 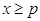 . Если существует . Если существует
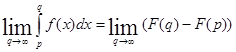 , ,
то этот предел обозначается 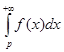 и называется сходящимся несобственным интегралом. и называется сходящимся несобственным интегралом.
Несобственные интеграл вида 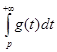 и аналогичный интеграл и аналогичный интеграл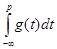 получаются при замене в интеграле Римана с помощью функции t=t(x), непрерывной и дифференцируемой на полуинтервале [a,b) ( или (a,b] ) и являющейся бесконечно большой определенного знака при получаются при замене в интеграле Римана с помощью функции t=t(x), непрерывной и дифференцируемой на полуинтервале [a,b) ( или (a,b] ) и являющейся бесконечно большой определенного знака при 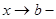 (или (или 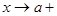 ). ).
Здесь существенно, что особой точкой функции t является именно конец (левый или правый) отрезка [a,b]. Если особой точкой t(x) (как в разобранном выше примере) является внутренняя точка с интервала (a,b), то 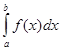 разбивается на разбивается на 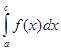 и и 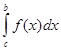 , и переход к аргументу t делается раздельно в каждом из слагаемых. , и переход к аргументу t делается раздельно в каждом из слагаемых.
Пример.
Вычислим  . .
Пусть  , ,
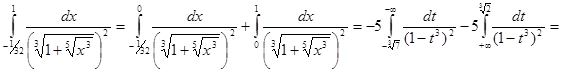

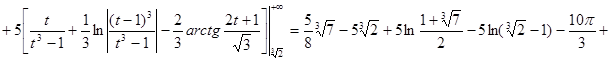
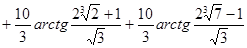
Другим видом несобственного интеграла является интеграл 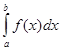 , если функция f не ограничена на , если функция f не ограничена на 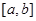 , но непрерывна на , но непрерывна на 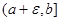 при любом при любом 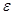 , , 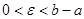 (или на (или на 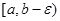 ), т.е. не ограничена в окрестности точки ), т.е. не ограничена в окрестности точки 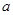 (точки b). (точки b).
Этот интеграл существует (сходится), если существует:
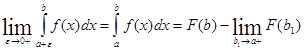
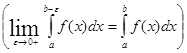
Пример.
 , если , если 
f(x) непрерывна на [0,1]. После замены  получаем получаем
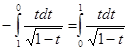 . .
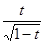 не ограничена на [0,1], т.к. первообразная функция не ограничена на [0,1], т.к. первообразная функция 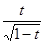 на на  при любом при любом 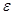 , ,  равна: равна:  , то , то
 . .
Несобственный интеграл может появится и при интегрировании по частям.

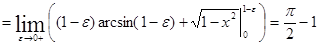 , ,
т.е.
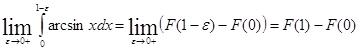 , ,
где 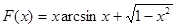 - первообразная для arcsinx на [0,1]. - первообразная для arcsinx на [0,1].
4.1.Формула Валлиса.
Для вывода формулы Валлиса необходимо вычислить следующий интеграл:
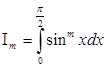 (при натуральном m). (при натуральном m).
Интегрируя по частям, найдём
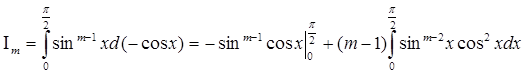 . .
Двойная подстановка обращает в нуль. Заменяя 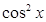 через через  , получим , получим
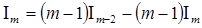
откуда рекуррентная формула:
 , ,
по которой интеграл 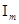 последовательно приводится к последовательно приводится к  и и 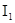 . Именно, при m=2n имеем . Именно, при m=2n имеем
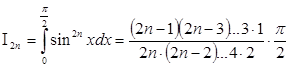 , ,
если же m=2n+1, то
 . .
Такие же точно результаты получаются и для 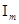 . .
Для более короткой записи найденных выражений воспользуемся символом m!!(произведение натуральных чисел, не превосходящих m и одной с ним чётности). Тогда можно будет написать
|  при m не при m не четном нечётном. четном нечётном.
|
|
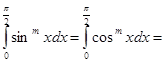 (1) (1) Из формулы (1) можно вывести знаменитую формулу Валлиса (J. Wallis).
Предполагая 0<x< , имеем неравенства , имеем неравенства
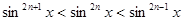 . .
Проинтегрируем эти неравенства в промежутке от 0 до  : :

Отсюда, в силу (1), находим

или
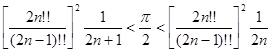 . .
Так как разность между двумя крайними выражениями
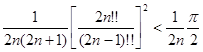 , ,
очевидно, стремится к 0 при 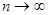 , то , то  является их общим пределом. Итак, является их общим пределом. Итак,

или
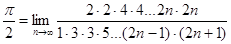 . .
Отсюда в свою очередь вытекает
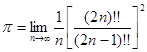
Эта формула носит название формулы Валлиса. Она дает довольно простое выражение числа p через натуральные числа. Теоретически этот результат интересен. Что касается ценности этой формулы как средства фактического вычисления p, то она невелика. Именно, чтобы получить удовлетворительную точность, надо взять n довольно большим, а тогда выражение  оказывается весьма громоздким. оказывается весьма громоздким.
4.2. Применение формулы Валлиса для интеграла Эйлера-Пуассона.
Интеграл Эйлера-Пуассона имеет вид:
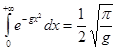 ; ;
Приведём метод его нахождения. Мы знаем что положив:
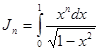 (т.к. (т.к. 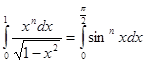 ), ),
имеем соотношение:
 ; ;
отсюда заключаем:
 , ,

что дает:
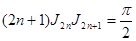 . .
Установив это, замечаем, что предел отношения  при бесконечно большом n равен единице; действительно, так как при бесконечно большом n равен единице; действительно, так как  убывает при возрастании n, то мы имеем неравенство: убывает при возрастании n, то мы имеем неравенство:
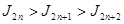
или:
 . .
Мы видим, следовательно, что 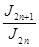 заключается между единицей и дробью заключается между единицей и дробью 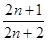 , которая также равна единице при бесконечном n. , которая также равна единице при бесконечном n.
Установив это, получаем равенство:
 , ,
которое нам дает, если заставим n бесконечно возрастать:
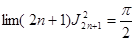 , ,
и, следовательно:
 . .
Полагая теперь 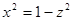 в интеграле в интеграле  , мы получим следующее новое выражение: , мы получим следующее новое выражение:
 ; ;
заменив затем z на  , получаем: , получаем:
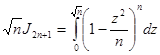
и, следовательно, при бесконечном n
 . .
Достаточно затем положить  , чтобы установить результат, к которому мы стремились: , чтобы установить результат, к которому мы стремились:
 . .
4.3. Вывод формулы Тейлора с остаточным членом в интегральной форме.
Формула интегрирования по частям: 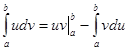 , ,
а обобщенная формула примет вид:
 . (1) . (1)
Положим, что в формуле (1) . Тогда . Тогда 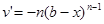 , , 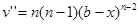 , …, , …, 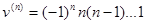 , , 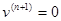 ; при x=b все функции v, v’, …, ; при x=b все функции v, v’, …,  обращаются в нуль. Пользуясь для u, u’, u’’, … функциональным обозначением f(x), f’(x), f’’(x), …, перепишем (1) в виде обращаются в нуль. Пользуясь для u, u’, u’’, … функциональным обозначением f(x), f’(x), f’’(x), …, перепишем (1) в виде

 . .
Отсюда получается формула Тейлора с дополнительным членом в виде определенного интеграла
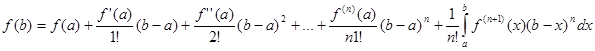 . .
Заменим здесь b через x, а  через через  : :
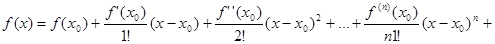
 . .
Новое выражение для дополнительного члена, не содержит никаких неизвестных чисел.
Если угодно, из этого выражения можно было бы вывести и уже знакомые нам формы дополнительного члена. Например, воспользовавшись тем, что множитель 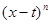 подинтегральной функции не меняет знака, можно применить к последнему интегралу обобщенную теорему о среднем подинтегральной функции не меняет знака, можно применить к последнему интегралу обобщенную теорему о среднем
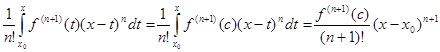 , ,
где с содержится в промежутке  . Таким образом, мы вновь получили лангранжеву форму дополнительного члена. . Таким образом, мы вновь получили лангранжеву форму дополнительного члена.
5. Заключение.
В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой рациональной варианты, а также вычисление интеграла Эйлера-Пуассона с помощью этой формулы. Рассмотрен способ получения формулы Тейлора с дополнительным членом в интегральной форме.
Формулой Валлиса в теоретических исследованиях пользуются и сейчас (например, при выведении формулы Стирлинга). Что касается фактического приближенного вычисления p, то существуют методы, гораздо более быстро ведущие к цели.
Интеграл Эйлера-Пуассона применяется при вычислении более сложных несобственных интегралов, встречается в теории вероятности.
Новое выражение для дополнительного члена в формуле Тейлора интересно тем, что оно не содержит никаких неизвестных чисел.
Данную курсовую работу можно использовать в качестве лекционного и справочного материала.
Список литературы
Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления»(II том) – Москва, 1970г.
Пискунов Н.С. «Дифференциальное и интегральное исчисления»(I том) - Москва, 1970г.
Эрмит Ш. «Курс анализа» - Москва, 1936г.
|