| Академия России
Кафедра Физики
Реферат
ОПЕРАТОРНЫЙ МЕТОД АНАЛИЗА переходных КОЛЕБАНИЙ в электрических цепях
Орел 2009
Содержание
Вступление
Основные свойства преобразования Лапласа
Законы Кирхгофа и Ома в операторной форме
Операторные схемы замещения
Литература
ВСТУПЛЕНИЕ
Действия над многозначными числами, как известно, существенно упрощаются при использовании логарифмов. Так операция умножения сводится к сложению логарифмов, деление – к вычитанию логарифмов и т. д. Каждому числу соответствует свой логарифм и поэтому логарифм можно рассматривать как своего рода изображение числа.
Так, например, 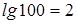 , следовательно, в этой системе 2 есть изображение числа 100. , следовательно, в этой системе 2 есть изображение числа 100.
В основе операторного метода также лежит понятие об изображении. Однако если в случае логарифмов речь шла об изображении числа, то в операторном методе используется изображение функций времени. Здесь каждой функции времени 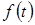 , определенной в области , определенной в области 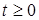 , соответствует некоторая функция новой переменной , соответствует некоторая функция новой переменной  и, наоборот, функции переменной и, наоборот, функции переменной 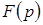 соответствует определенная функция времени соответствует определенная функция времени 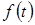 . .
Функция 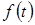 называется оригиналом, функция называется оригиналом, функция 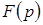 – изображением, а переменная – изображением, а переменная 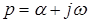 – оператором. – оператором.
Фраза "функция 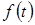 имеет своим изображением имеет своим изображением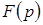 " условно записывается так " условно записывается так 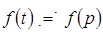 . .
Знак 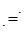 называют знаком соответствия. называют знаком соответствия.
Основанный на таком представлении функций метод получил название операторного и используется для аналитического решения линейных дифференциальных
и интегро-дифференциальных уравнений в теории электрических цепей. Решение задачи при этом как бы разбивается на 3 этапа.
На первом этапе осуществляется переход из временной области в операторную, на втором – решение задачи в операторной форме и на третьем – обратный переход в область реального времени.
Основные свойства преобразования Лапласа
Нахождение изображений функции времени (равно как и обратные переходы от изображений к оригиналу) выполняются с помощью специальных интегральных преобразований, приводимых в курсе высшей математики. В настоящее время в большей части современной технической литературы операторные методы связывают с применением преобразования Лапласа, в основе которого лежит соотношение:
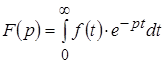 . .
Важно отметить, что функции, описывающие реально возможные воздействия и соответствующие им реакции, всегда преобразуемы по Лапласу. Полученную в результате такого преобразования функцию называют иногда лапласовым изображением функции 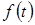 или ее или ее 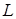 -изображением и обозначают: -изображением и обозначают:
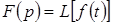 . .
Отыскание 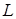 -изображения заданной функции называется прямым преобразованием Лапласа, а нахождение -изображения заданной функции называется прямым преобразованием Лапласа, а нахождение 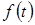 по известному по известному 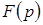 – обратным преобразованием Лапласа. – обратным преобразованием Лапласа.
Основные свойства и правила этих преобразований:
Свойство единственности
.
Каждому оригиналу (исходной функции) соответствует единственное изображение и наоборот, каждому изображению соответствует единственный оригинал.
Свойство линейности.
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений:
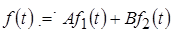 – оригинал; – оригинал;
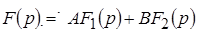 – изображение. – изображение.
Преобразование операции дифференцирования.
Если оригинал 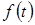 представляет производную от некоторой функции представляет производную от некоторой функции
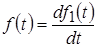 , ,
то его изображение имеет вид:
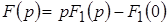 . .
При нулевых начальных условиях (ННУ) 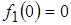 и и 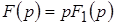 , т. е. дифференцированию оригинала соответствует умножение его изображения на оператор , т. е. дифференцированию оригинала соответствует умножение его изображения на оператор  (при ННУ). (при ННУ).
Преобразование операции интегрирования
.
Если оригинал представляет от некоторой функции интеграл:
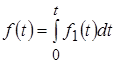 , ,
то его изображение имеет вид: 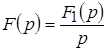 , т. е. интегрированию оригинала соответствует деление его изображения на оператор , т. е. интегрированию оригинала соответствует деление его изображения на оператор  . .
Теорема запаздывания (оригинала)
.
Если 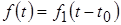 , то , то 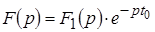 , где , где 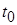 — время запаздывания, т. е. запаздыванию оригинала на время — время запаздывания, т. е. запаздыванию оригинала на время 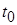 соответствует умножение его изображения на экспоненциальный множитель соответствует умножение его изображения на экспоненциальный множитель 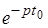 . .
Теорема смещения (изображения).
Если 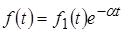 , то , то 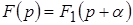 , т. е. умножению оригинала на экспоненциальный множитель , т. е. умножению оригинала на экспоненциальный множитель 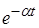 соответствует смещение его изображения на величину соответствует смещение его изображения на величину 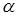 . .
Решение задач прямого и обратного преобразований Лапласа существенно упрощаются в тех случаях, когда удается использовать справочные таблицы, которые содержат пары оригинал – изображение. Эти таблицы приводятся в справочниках.
Следует учесть, что при обратном преобразовании Лапласа полученные функции иногда не подходят под табличные. В этом случае используется разложение этой функции на простые дроби или в ряд с последующим применением обратного преобразования Лапласа.
Законы Кирхгофа и Ома в операторной форме
Возможность существенного упрощения решения задачи анализа колебаний в электрических цепях операторным методом основывается на том, что для 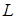 -изображений колебаний формально верны законы Кирхгофа и Ома. -изображений колебаний формально верны законы Кирхгофа и Ома.
Действительно, согласно первому закону Кирхгофа:
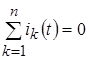
Если обе части этого равенства подвергнуть преобразованию Лапласа, то оно переходит в равенство:
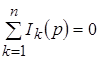 , ,
и следовательно, алгебраическая сумма 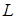 -изображений токов в любом узле цепи равна нулю
. Аналогично доказывается справедливость второго закона Кирхгофа для операторных напряжений в контуре: -изображений токов в любом узле цепи равна нулю
. Аналогично доказывается справедливость второго закона Кирхгофа для операторных напряжений в контуре:
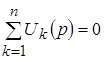 . .
При выводе закона Ома в операторной форме будем полагать, что реактивные элементы находятся при ННУ (конденсатор разряжен, через катушку индуктивности не протекает ток).
Рассмотрим соотношения в элементах электрических цепей.
Элемент резистивного сопротивления.
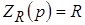 – операторное резистивное сопротивление, – операторное резистивное сопротивление,
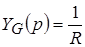 – резистивная операторная проводимость. – резистивная операторная проводимость.
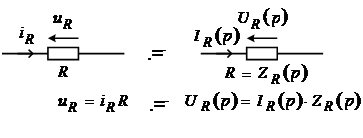
Таким образом, операторное напряжение на резистивном сопротивлении равно произведению сопротивления на величину операторного тока.
Элемент индуктивности.
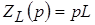 – операторное индуктивное сопротивление, – операторное индуктивное сопротивление,
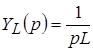 – операторная индуктивная проводимость. – операторная индуктивная проводимость.
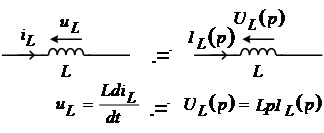
Следовательно, операторное напряжение на индуктивности равно произведению операторного индуктивного сопротивления на величину операторного тока.
Элемент емкости.
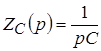 – операторное емкостное сопротивление, – операторное емкостное сопротивление,
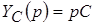 – операторная емкостная проводимость. – операторная емкостная проводимость.
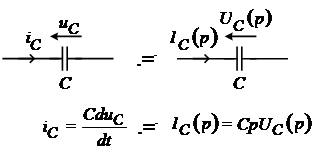
Операторное напряжение на емкости равно произведению операторного емкостного сопротивления на величину операторного тока.
Выражения
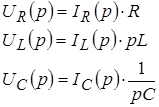
представляют закон Ома в операторной форме.
Выводы:
– законы Кирхгофа и Ома справедливы и в операторной форме, причем закон Ома справедлив только при нулевых начальных условиях;
– все ранее изученные методы анализа электрических цепей (метод контурных токов, метод узловых напряжений, метод эквивалентного генератора и др.) справедливы и в операторной форме.
Операторные схемы замещения реактивных элементов
при ненулевых начальных условиях
Часто коммутация осуществляется в момент времени, когда реактивные элементы обладают энергией. В этом случае они находятся при ненулевых начальных условиях и к ним нельзя применить закон Ома в операторной форме. Для устранения этого препятствия используют прием, суть которого состоит в том, что физически один реактивный элемент искусственно заменяют двумя: операторным источником, отражающим энергию реактивного элемента на момент коммутации, и самим реактивным элементом, но находящимся теперь уже при нулевых начальных условиях. Такое изображение называется схемой замещения. Ее можно получить, используя свойства преобразования Лапласа:
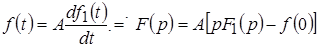 . .
Так, для индуктивности с током схемы замещения имеют вид, показанный на рисунке 1.

а) б) в)
Рис. 1
Они являются следствием преобразования следующих выражений:
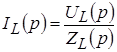 ; ; 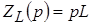
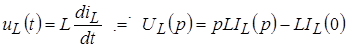
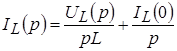
Здесь следует иметь в виду два обстоятельства: направление операторного тока должно совпадать с направлением тока через индуктивность в момент непосредственно предшествующий коммутации и второе, что реально существует один элемент, поэтому операторный ток через индуктивность в схеме замещения определяется в общей ветви (рис. 1б).
Заряженная емкость отображается схемами замещения, показанными на рисунке 2б, в.
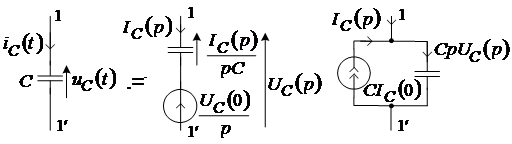
а) б) в)
Рис. 2
Они являются следствием преобразования следующих выражений:
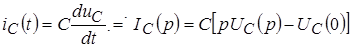 , ,
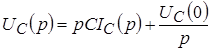 . .
Здесь напряжение операторного источника совпадает с напряжением на емкости до коммутации, а операторное напряжение на емкости определяется между зажимами 1 – 1¢.
Применение операторных схем замещения реактивных элементов, находящихся при ненулевых начальных условиях, дает возможность применять закон Ома в операторной форме, что широко используется на практике и, в частности, при рассмотрении свободных колебаний в электрических цепях. Известно, что такие колебания возникают за счет энергии, запасенной реактивными элементами при отключении внешних источников. Следует иметь в виду, что указанная коммутация может осуществляться как путем механического отключения, так и путем гашения источников. В последнем случае источник напряжения заменяется коротким замыканием, а источник тока – обрывом.
При решении задач приходится осуществлять переход от обычной к операторной схеме. Если реактивные элементы находятся при ННУ, то такой переход не вызывает особых затруднений. Например, на рисунке 3, а показана исходная схема, а на рисунке 3, б – эквивалентная ей операторная.
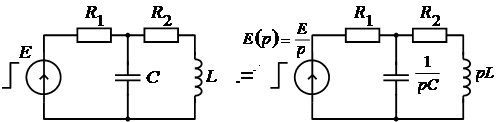
а) б)
Рис. 3
Если же реактивные элементы находятся при ненулевых начальных условиях, то в операторной схеме они должны быть отображены схемами замещения.
Пример.
Пусть в цепи, изображенной на рисунке 4 в момент 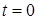 замыкается ключ "К
". Требуется определить эквивалентную ей операторную схему. замыкается ключ "К
". Требуется определить эквивалентную ей операторную схему.
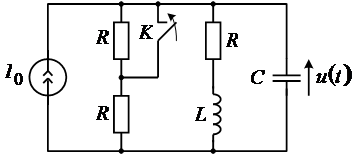
Рис. 4
Так как реактивные элементы в данном случае находятся при ненулевых начальных условиях, то предварительно следует определить 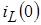 и и 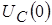 . Для этого изобразим эквивалентную схему цепи при . Для этого изобразим эквивалентную схему цепи при 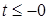 (рис. 5). (рис. 5).
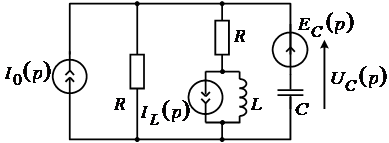
Рис. 5
Видно, что 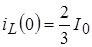 ; ; 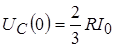 . .
Таким образом 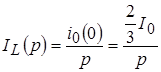 ; ; 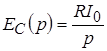 и соответствующая этому схема показана на рисунке 6. и соответствующая этому схема показана на рисунке 6.
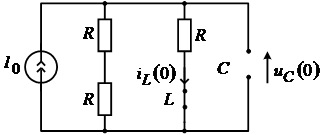
Рис. 6
Далее находится требуемая реакция в операторной форме, а затем осуществляется переход в область реального времени.
Вывод: нахождение реакций при ненулевых начальных условиях требует применения схем замещения в операторной форме и является более сложной задачей, чем при ННУ.
Литература
1. Белецкий А. Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986.
2. Шалашов Г. В. Переходные процессы в электрических цепях. – Орел: ОВВКУС 1981.
|