| Лабораторная работа № 2
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ПРОЗРАЧНОЙ ЖИДКОСТИ ПО МЕТОДУ СТОКСА
Цель работы:
ознакомиться с методом определения коэффициента вязкости прозрачной жидкости методом движущегося в жидкости шарика.
Оборудование:
стеклянный цилиндр, с прозрачной жидкостью; секундомер; микрометр; масштабная линейка; шарики из свинца.
Теория вопроса и метод выполнения работы
Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества. К явлениям переноса относятся диффузия, внутреннее трение и теплопроводность.
Явлением внутреннего трения (вязкости) называется появление сил трения между слоями газа или жидкости, движущимся, друг относительно друга, параллельно и с разными по величине скоростями. Слой, движущийся быстрее, действует с ускоряющей силой на более медленно движущийся соседний слой. Силы внутреннего трения, которые возникают при этом, направлены по касательной к поверхности соприкосновения слоев (рис. 1, 2).
Величина силы внутреннего трения 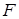 между соседними слоями пропорциональна их площади между соседними слоями пропорциональна их площади 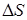 и градиенту скорости и градиенту скорости 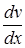 , то есть справедливо соотношение, полученное экспериментально Ньютоном , то есть справедливо соотношение, полученное экспериментально Ньютоном
 .(1) .(1)
Величина 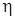 называется коэффициентом внутреннего трения или динамическим коэффициентом вязкости. В СИ называется коэффициентом внутреннего трения или динамическим коэффициентом вязкости. В СИ 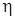 измеряется в измеряется в  . .
Входящая в (1) величина 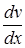 показывает, как меняется скорость жидкости в пространстве при перемещении точки наблюдения в направлении, перпендикулярном слоям. Понятие градиента скорости иллюстрируется рис. 1, 2. показывает, как меняется скорость жидкости в пространстве при перемещении точки наблюдения в направлении, перпендикулярном слоям. Понятие градиента скорости иллюстрируется рис. 1, 2.

Рис. 1. Постоянный градиент скорости
На рисунке 1 показано распределение скоростей слоев жидкости между двумя параллельными пластинами, одна из которых неподвижна, а другая имеет скорость  . Подобная ситуация возникает в прослойке смазки между движущимися деталями. В этом случае слои жидкости, непосредственно прилегающие к каждой из пластин, имеют одинаковую с ней скорость. Движущиеся слои частично увлекают за собой соседние. В результате в пространстве между пластинами скорость жидкости меняется по направлению . Подобная ситуация возникает в прослойке смазки между движущимися деталями. В этом случае слои жидкости, непосредственно прилегающие к каждой из пластин, имеют одинаковую с ней скорость. Движущиеся слои частично увлекают за собой соседние. В результате в пространстве между пластинами скорость жидкости меняется по направлению  равномерно. Таким образом, здесь равномерно. Таким образом, здесь
 . .

Рис. 2. Переменный градиент скорости
На рисунке 2 показано распределение скоростей жидкости около движущегося в ней вертикально вниз со скоростью  шарика. шарика.
Предполагается, что скорость  мала, так что завихрения в жидкости не образуются. В этом случае жидкость, непосредственно прилегающая к поверхности шарика, имеет скорость мала, так что завихрения в жидкости не образуются. В этом случае жидкость, непосредственно прилегающая к поверхности шарика, имеет скорость  . В это движение частично вовлекаются удаленные от шарика слои жидкости. При этом скорость наиболее быстро меняется по направлению . В это движение частично вовлекаются удаленные от шарика слои жидкости. При этом скорость наиболее быстро меняется по направлению  вблизи шарика. вблизи шарика.
Наличие градиента скорости у поверхности тела указывает, что на него действует сила внутреннего трения, зависящая от коэффициента вязкости 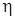 . Сама величина . Сама величина 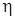 определяется природой жидкости и обычно существенно зависит от ее температуры. определяется природой жидкости и обычно существенно зависит от ее температуры.
Сила внутреннего трения и коэффициент вязкости жидкости может быть определен различными методами – по скорости истечения жидкости через калиброванное отверстие, по скорости движения тела в жидкости и т.д. В данной работе для определения 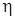 используется метод, предложенный Стоксом. используется метод, предложенный Стоксом.
Рассмотрим для примера равномерное движение маленького шарика радиуса 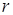 в жидкости. Обозначим скорость шарика относительно жидкости через в жидкости. Обозначим скорость шарика относительно жидкости через  . Распределение скоростей в соседних слоях жидкости, увлекаемых шариком, должно иметь вид, изображенный на рис. 2. В непосредственной близости к поверхности шара эта скорость . Распределение скоростей в соседних слоях жидкости, увлекаемых шариком, должно иметь вид, изображенный на рис. 2. В непосредственной близости к поверхности шара эта скорость  равна равна  , а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии , а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии  от поверхности шара. от поверхности шара.
Очевидно, чем больше радиус шара, тем большая масса жидкости вовлекается им в движение, и  должно быть пропорционально радиусу шарика должно быть пропорционально радиусу шарика 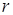 : :  . Тогда среднее значение градиента скорости на поверхности шара равно . Тогда среднее значение градиента скорости на поверхности шара равно
 . .
Поверхность шара  , и полная сила трения, испытываемая движущимся шаром, равна , и полная сила трения, испытываемая движущимся шаром, равна
 . .
Более подробные расчеты показывают, что для шара  , окончательно , окончательно  – формула Стокса. – формула Стокса.
По формуле Стокса можно, например, определить скорости оседания частиц тумана и дыма. Ею можно пользоваться и для решения обратной задачи – измеряя скорость падения шарика в жидкости, можно определить ее вязкость.
Упавший в жидкость шарик движется равноускоренно, но, по мере того, как растет его скорость, будет возрастать и сила сопротивления жидкости до тех пор, пока сила тяжести шарика в жидкости не сравняется с суммой силы сопротивления и силы трения жидкости движению шарика. После этого движение будет происходить с постоянной скоростью  . .
При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движение, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика. Таким образом, при вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.
Если шарик падает в жидкости, простирающейся безгранично по всем направлениям 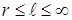 , не оставляя за собой никаких завихрений (малая скорость падения, маленький шарик), то, как показал Стокс, сила сопротивления равна , не оставляя за собой никаких завихрений (малая скорость падения, маленький шарик), то, как показал Стокс, сила сопротивления равна
 ,(2) ,(2)
где  – коэффициент внутреннего трения жидкости; – коэффициент внутреннего трения жидкости; 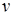 – скорость шарика; – скорость шарика; 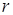 – его радиус. – его радиус.
Кроме силы 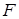 на шарик действует сила тяжести на шарик действует сила тяжести 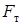 и архимедова сила и архимедова сила 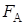 , равная весу , равная весу  вытесненной шариком жидкости. Для шара вытесненной шариком жидкости. Для шара
 ; ;  ,(3) ,(3)
где 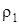 , , 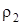 – плотность материала шарика и исследуемой жидкости. – плотность материала шарика и исследуемой жидкости.
Все три силы будут направлены по вертикали: сила тяжести – вниз, подъемная сила и сила сопротивления – вверх. Первое время, после вхождения в жидкость, шарик движется ускоренно. Считая, что к моменту прохождения шариком верхней метки скорость его уже установилась, получим
 , ,
где  – время прохождения шариком расстояния между метками, – время прохождения шариком расстояния между метками, 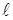 – расстояние между метками. – расстояние между метками.
Движения шарика возрастает, ускорение уменьшается и, наконец, шарик достигнет такой скорости, при которой ускорение становится равным нулю, тогда
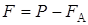 .(4) .(4)
Подставляя в равенство (4) значение величин, получим:
 .(5) .(5)
Решая уравнение (5) относительно коэффициента внутреннего трения, получаем расчетную формулу:
 .(6) .(6)

Рис. 3. Прибор Стокса
На рисунке 3 представлен прибор, состоящий из широкого стеклянного цилиндра с нанесенными на него двумя кольцевыми горизонтальными метками  и и  ( ( – расстояние между метками), который наполняется исследуемой жидкостью (касторовое масло, трансформаторное масло, глицерин) так, чтобы уровень жидкости был на 5¸8 см выше верхней метки. – расстояние между метками), который наполняется исследуемой жидкостью (касторовое масло, трансформаторное масло, глицерин) так, чтобы уровень жидкости был на 5¸8 см выше верхней метки.
Порядок выполнения работы
Для измерения коэффициента внутреннего трения жидкости, например, масла, берутся очень маленькие шарики. Диаметр этих шариков измеряют микрометром. Время падения шарика – секундомером.
1. С помощью микрометра измерьте диаметр шарика.
2. Измерьте время опускания каждого шарика между двумя метками  и и  . Шарик опустите в отверстие воронки и в момент прохождения через верхнюю метку включите секундомер, а в момент прохождения через нижнюю метку его выключите. . Шарик опустите в отверстие воронки и в момент прохождения через верхнюю метку включите секундомер, а в момент прохождения через нижнюю метку его выключите.
3. Проведите опыт не менее пяти раз.
4. Измерьте расстояние между метками. Вычислите скорость движения шарика и по формуле (5) найдите значение коэффициента вязкости.
5. Плотность жидкости и шариков возьмите из таблицы физических величин.
6. Найдите среднее значение коэффициента вязкости, оценить абсолютную и относительную погрешности измерений.
| №
п/п
|

|

|

|

|

|

|

|

|

|

|
| м
|
м
|
м
|
с
|
м/с
|
H×c/м2
|
H×c/м2
|
H×c/м2
|
H×c/м2
|
%
|
| 1
|
| 2
|
| 3
|
| 4
|
| 5
|
Контрольные вопросы
1. В чем заключается метод определения коэффициента вязкости жидкости по Стоксу?
2. Какие силы действуют на шарик при его движении в жидкости?
3. Как зависит коэффициент внутреннего трения жидкостей от температуры?
4. Какие течения жидкости называют ламинарными и турбулентными? Как определяются числом Рейнольдса эти течения?
5. Каков физический смысл коэффициента вязкости жидкости?
6. Почему измерения верны только при малых скоростях?
7. Для какой жидкости глицерина или воды коэффициент вязкости можно определить точнее рассматриваемым методом?
8. Имеется два свинцовых шарика разного диаметра. У какого из них скорость падения в жидкости будет больше?
9. Охарактеризуйте другие явления переноса (диффузию и теплопроводность). Каким законам они подчиняются?
|