| Міністерство освіти і науки України
Прикарпатський національний університет імені Василя Стефаника
Факультет математики та інформатики
кафедра диференціальних рівнянь і прикладної математики
Курсова робота на тему:
Деякі скінченно-різнецеві методи розв’язування
звичайних диференціальних рівнянь
Виконав:
студент групи ПМ-41
Васьків Святослав
Перевірив:
науковий керівник:
Василишин П.Б.
Івано-Франківськ 2010
План
Вступ.
1. Чисельна ітерація рівнянь Ньютона
2. Алгоритм Бімана і Шофілда
3. Метод Рунге-Кутта
a) Метод Рунге — Кутта 4-го порядку
б) Неявні схеми Рунге-Кутта
в) Неявні інтерполяційні схеми
г) Програма Рунге-Кутта на мові С#
д) Програма Beeman
4. Метод Адамса
5.Метод Крилова
6. Метод Чаплигіна
Висновок
Список використаної літератури
Вступ
Приведемо декілька найбільш відомих скінченно-різнецевих методів рішення рівнянь руху з непереривною силою. Важливо пам'ятати про те, що успішне використання чисельного метода визначається не лише тим, наскільки добре він наближає похідну на кожному кроці, але і тим, наскільки добре він апроксимує інтеграли руху, наприклад повну енергію. Безліч алгоритмів, використовуються в наш час, свідчить про те, що жоден метод не перевершує по усіх параметрах усіх інших.
1. Чисельна ітерація рівнянь Ньютона
Для спрощення запису розглянемо одновимірний рух частини і запишемо рівняння Ньютона у виді:
 (1)
(1)
 (2) (2)
Метою усіх скінцеворізнецевих методів являється знаходження значень x
n
+1
і v n+1
(точка в "фазовому просторі") у момент часу tn+1
=tn
+∆t
Нам вже відомо, що величину кроку ∆t потрібно вибирати таким чином, щоб метод інтегрування породжував приймати однакове рішення. Один із способів перевірки стійкості методу полягає в контролі величини повною енергії і забезпеченні того, щоби вона не відхилялася від початкового значення у разі, коли повна енергія зберігалась. Досить велике значення кроку приводить до не збереження повної енергії і до різних розв’язків для хn
+1
i vn+1
, тобто до таких розв’язків, які все більше відхиляються з потоком часу від істинного розв’язку.
Суть багатьох алгоритмів, можна зрозуміти, розкладаючи
vn
+1
≡ v(tn
+∆t) i
xn
+1
≡ x(tn
+∆t ) в ряд Тейлора. Запишемо
 (3) (3)
і
 (4) (4)
Добре відомий метод Ейлера еквівалентний збереженню в формулі (3) членів 
 (5) (5)
і
 (6) (6)
Оскільки ми утримали у формулах (5-6) члени порядку ∆t, то «локальна» погрішність (погрішність на кроці) складає величину O(∆t)2
Оскільки ми від кроку до кроку погрішності накопичуються, позтому можна припускати, що «глобальна» погрішність, що є сумарною погрішністю за розглядом проміжок часу, буде величиной O(∆t). Ось ця оцінка погрішності цілком правдоподібна, оскільки число кроків, на яке розбивається часовий інтервал, пропорційна  1/∆t
. Звідси випливає, порядок глобальної погрішності збільшується в ∆t
разів по відношенню до локальної погрішності. Оскільки прийнято "говорити, що метод має n-й порядок аппроксимації, якщо ця локальна погрішність рівна О((∆t)n
+1
), то метод Ейлера відноситься до методів першого порядку. 1/∆t
. Звідси випливає, порядок глобальної погрішності збільшується в ∆t
разів по відношенню до локальної погрішності. Оскільки прийнято "говорити, що метод має n-й порядок аппроксимації, якщо ця локальна погрішність рівна О((∆t)n
+1
), то метод Ейлера відноситься до методів першого порядку.
Метод Ейлера являється асиметричним, оскільки він просуває вирішення на один часовий крок ∆t, а використовує при цьому інформацію про похідну тільки в початковій точці інтервалу. Ми вже переконалися в тому, що точність методу Ейлера обмежується і частенько породжуване його рішення нестійке. На щастя, як правило, немає необхідності використовувати більш складні алгоритми. Наприклад, швидше ми знайшли, що проста модифікація методу (5-6), запропонована Кромером і іншими авторами, породжує стійке рішення для коливальних систем. Для закріплення повторимо алгоритм Ейлера-Кромера або наближення по «останній точці»:
 (7) (7)
і
 (8) (8)
Мабуть найбільш очевидний шлях удосконалення методу Ейлера, полягає в використанні для обрахування нового значення координати середини на відрізку швидкості. Відповідний метод середньої точки
можна записати в вигляді:
 (9) (9)
і
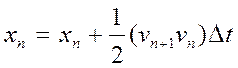 (10) (10)
Замітимо, що якщо підставити вираз (9) для vn
+1
в (10) то отримаємо
 (11) (11)
Звідси випливає, що метод середньої точки другого порядку точності по координаті і першого порядку по швидкості. Хоча наближення по середній точці дає точні результати для випадку постійного прискорення, взагалом він не приводить до значного покращення результату, ніж метод Ейлера. На справді оці два методи однаково погані, оскільки з кожним кроком погрішність збільшується.
Метод напівкроку відноситься до методів більше за високого порядок точностіз обмеженою погрішністю. Приймається, що средияя скорість на відрізку рівна значенню швидкості в середиие відрізок. Метод напівкроку можна записати у виді:
 (12) (12)
і
 (13) (13)
Замітио, що метод напів кроку не являє собою «самостартючим», так чи однакще фомули не дозволять порахвати v1/2.
Цю незручність модна здолати поклавши
 (14) (14)
Оскільки формули (12-14) можна повторювати до безмежності, то метод напів кроку отримав широке розповсюдження в навчальній літературі.
Один із найбільш відомих алгоритмів вищого порядку привласнюєтья Верле. Запишемо в ряд Тейлора для хn
-1
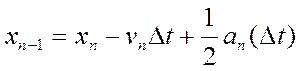
(15)
Якщо скласти формули інтегрування вперед і назад (вирази (3) і (14) відповідно) то отримаємо
 (16) (16)
або
 (17 ) (17 )
Аналогічно розв'язання розкладу в ряд Тейлора для xn
+1
i
xn
-1
дає
 (18) (18)
Підмітимо, що звязок з алгоритом Верле (18)
велика погрішність має третій порядок для координати і другий порядок для швидкості. Проте швидкість не бере участі в інтегруванні рівнянь руху. В літературі по чисельному аналізу алгоритм Верле називається «неявна симетричність різновидної схеми».
Менш відомим, про те математично еквівалентної версії алгоритму Верле являє собою схема
  (19) (19)
і
 (20) (20)
Видно, що схема (19-20), називається швидкісною формулою алгоритму Верле, являється самостартуючою і не приводить до накопичення погрішностей округлення. Формули (19-20) можна вивести із формул (16-19) наступним чином.. Спочатку додамо і віднімемо із рівнянь (16-19) по (1/2)хn
+1
і запишемо:

 (21) (21)
Тут ви використаємо вираз (18). Із (17) знайдемо аn
для метода Верле:
 (22) (22)
Легко помітити, що підстановка (22)в вираз (21) приводить до (19). В томуж дусі перепишемо (17) для vn
+1
 (23) (23)
Тепер перепишемо формулу (17) для хn
+2
і підтавимо її в отриманий результат формули (23). Отримуємо:
 (24)
(24)
Тоді використовуємо вираз (17) для xn
+1,
повторимо цю процедуру і поставимо xn
+1
в (24); після не важких перестановок отримаємо потрібний результат (20)
2. Алгоритм Бімана і Шофілда
Інший корисний алгоритм, в якому немає нагромаження погрішностей округлення, як в алгоритмі Верле, належить Біміану і Шофілду. Запишемо алгоритм Бімана в наступному виді:
 (25а) (25а)
і
 (25б) (25б)
Підмітимо, що точність розразунку траєктторії по схемі (25) не вища, ніж в алгоритмі Верле. Її перевага заключається в тому, що просто вона краще зберігає енергію. Однак алгоритм Бімана не самостартуючий. Алгорим Бімана і алгоритм Верле в швидкісній вормулі викоритані в програмі BEEMAN
Завершимо наше обговорення оротким викладом двох методів, які зазвичай приводяться в підручниках по чисельному аналізу. Один приклад метода предиктор:
 (26а)
(26а)
Передбучуване значення коодринати дозволить оприділити прискорення 
Тоді, використовуючи  , отримаємо скоректироване з
начення vn
+1
і xn
+1 , отримаємо скоректироване з
начення vn
+1
і xn
+1
коректор: 
 (26б)
(26б)
Скоректироване значення xn
+1
використовується для визначення нового передбачуваного значення аn
+1
і, значить, нових передбачених значень vn
+1
i xn
+
r
Ця процедура повторяється до тих пір, доки передбачення і скоррективонане значення xn
+1
відрізняються менше ніж на задану величину! Даний метод можна розробити на схемі більш високого порядку, які зв’язуються між собою не тільки xn
+1 ,
xn
і vn
, але і так само значеннями vn
-1
і vn
-2.
Замітимо, що метод предиктора-коректора не являється самостартуючим.
3. Метод Рунге-Кутта
Для пояснення методу Рунге-Кутта подивимось спочатку розв’язок диференціального рівняння першого порядку
 (27) (27)
Метод Рунге-Кутти другого порядку
для розв’язку рівняння (27) модна, використовуючи стандартні значення, записати наступним чином:
 (28) (28)
Сенс формул (28) полягає у наступному: В методі Ейлера допускається, що для екстаполяції в наступну точку модна використовувати нахил кривої f(xn
,yn
)в точці (xn
,yn
) так чи однакше yn
+1
=yn
+f(xn
,yn
)*∆x. Однак можна повисити почність оцінки нахилу, якщо методом Ейлера повести екстраполяцію в середню
точку відрізку, а потім використати центральну похідну на всьому відрізку. Звідси оцінка нахилу в методі Рунге-Котти рівна
 де де 
Застосування методу Рунге-Кутти до рівнянь руху Ньютона дає
 (29) (29)
Оскільки методи Руиге-Кутти є такими, що самостартуючими, то їх часто використовують для вираховання декількох перших кроків для несамостартуючих алгоритмів.
4. Метод Рунге — Кутта 4-го порядку
Цей метод настільки широко розповсюджений, що його часто називають просто методом Рунге — Кутта.
Розглянемо задачу Коші для системи диференціальних рівнянь довільного порядку, що записується у векторній формі як:
 
Тоді значення невідомої функції в точці xn
+1
обчислюється відносно значення в попередній точці xn
по такій формулі:

де h— крок інтегрування, а коефіцієнти k n
розраховуються наступним чином:

Це метод 4-го порядку, тобто похибка на кожному кроці становить O
(
h
5
)
,
а сумарна похибка на кінцевому інтервалі інтегрування є величиною O
(
h
4
)
.
Прямі методи Рунге — Кутта
Група прямих методів Рунге — Кутта є узагальненням методу Рунге — Кутти 4-го порядку. Воно задається формулами

де


Конкретний метод визначається числом s
і коефіцієнтами bi
,
aij
i
ci
. Ці коефіцієнти часто впорядковують в таблицю
 0 0
c2
a21
c3
a31
a32
∙ ∙ ∙ ∙
∙ ∙ ∙ ∙
∙ ∙ ∙ ∙
cs
as1
as2
∙ ∙ ∙
as,s − 1
b1
b2
bs − 1
bs
Для коефіцієнтів методу Рунге — Кутта мають справджуватись умови

Якщо ми хочемо, щоб метод мав порядок p
, то варто так само забезпечити умову  — наближення, отримане по методу Рунге — Кутти. Після багаторазового диференціювання ця умова перетвориться в систему поліноміальних рівнянь на коефіцієнти методу. — наближення, отримане по методу Рунге — Кутти. Після багаторазового диференціювання ця умова перетвориться в систему поліноміальних рівнянь на коефіцієнти методу.
5. Неявні схеми Рунге-Кутта
Викладений тут алгоритм є неявна схема Рунге-Кутта четвертого порядку. У неї, як завжди, вбудована оцінка погрішності, яка дорівнює різниці відповідей четвертого і третього порядків точності, вычисленних по використаних точках. Іншими словами, в порівнянні з рекомендованим вище явним методом Рунге-Кутта п'ятого порядку, усі порядки в точності на одиницю менше. Нагадаємо, що в методі Рунге-Кутта п’ятого порядку використовується шість точок. У неявній схемі точок буде значно менше, оскільки для неявних схем зв'язок порядку точності з кількістю використаних точок не така, як для явних схем. Наприклад, як ми вже бачили, одноточкова неявна схема може мати другий порядок точності. У нашій неявній схемі четвертого порядку ми обійдемося всього-навсього трьома точками:





На перший погляд, слід спочатку вичислити матрицю  , а потім застосовувати її потрібну кількість разів до усім f
j
. Проте, як ми знаєм (див. частину I, розділ "Системи лінійних рівнянь"), це не є правильний спосіб рішення СЛР "про запас". Правильний спосіб рішення СЛР з цією матрицею , а потім застосовувати її потрібну кількість разів до усім f
j
. Проте, як ми знаєм (див. частину I, розділ "Системи лінійних рівнянь"), це не є правильний спосіб рішення СЛР "про запас". Правильний спосіб рішення СЛР з цією матрицею  раз і назавжди (для довільної правої частини) - це LU - розкладання матриці раз і назавжди (для довільної правої частини) - це LU - розкладання матриці  . При цьому матриця . При цьому матриця  розкладається на ліву нижню трикутну матрицю L і праву верхню трикутну матрицю U. Після цього рішення будь-хто СЛР з матрицею розкладається на ліву нижню трикутну матрицю L і праву верхню трикутну матрицю U. Після цього рішення будь-хто СЛР з матрицею  будується за допомогою прямої підстановки (для матриці L) і потім зворотної підстановки (для матриці U). Кожна з підстановок вимагає N2
операцій. У нашому випадку має сенс скомбінувати праві частини усіх СЛР так, щоб кількість застосувань матриці будується за допомогою прямої підстановки (для матриці L) і потім зворотної підстановки (для матриці U). Кожна з підстановок вимагає N2
операцій. У нашому випадку має сенс скомбінувати праві частини усіх СЛР так, щоб кількість застосувань матриці  (точніше, кількість СЛР, які потрібно вирішити) була мінімальною. Для цього досить ввести проміжні змінні (точніше, кількість СЛР, які потрібно вирішити) була мінімальною. Для цього досить ввести проміжні змінні  . В результаті ми отримаємо наступний рецепт для одного кроку за часом t→t + h. . В результаті ми отримаємо наступний рецепт для одного кроку за часом t→t + h.
Алгоритм:
Для поточної точки  обчислюваний обчислюваний 
Крім того, вираховуєм 
Виконуємо LU - розкладання матриці А. (Це робиться один раз і назавжди для цього кроку за часом t→t + h
).
За допомогою LU-розкладання обчислюємо  . Обчислюваний . Обчислюваний  . Обчислювано . Обчислювано  . З допомогою LU - розкладання обчислюваний . З допомогою LU - розкладання обчислюваний 
Обчислюємо 
Обчислюваний  . .
За допомогою LU розкладання обчислюємо
 
За допомогою LU розкладання обчислюваний

Обчислюємо значення   : :

Обчислюємо погрішність  
- Перетворюємо вектор Е на одне число є, що характеризує погрішність на цьому кроці.
Ця схема призводить до досить забавної поведінки "швидких" змінних. Поведінка виявляється абсолютно однаковою як у разі релаксаційного рівняння  , так і у разі осциляторного рівняння , так і у разі осциляторного рівняння  . Саме, при Ch>>1 "швидкі" змінні експоненциально вибуваєть, причому швидкість вибування абсолютно не залежить від величини C: x(t+h)=x(t)/3
. Отже стійкість гарантована, але сподіватися на правильний опис еволюції "швидких" змінних не доводиться. . Саме, при Ch>>1 "швидкі" змінні експоненциально вибуваєть, причому швидкість вибування абсолютно не залежить від величини C: x(t+h)=x(t)/3
. Отже стійкість гарантована, але сподіватися на правильний опис еволюції "швидких" змінних не доводиться.
Повний алгоритм рішення системи ОДУ з адаптивною зміною кроку будується на основі цього рецепту таким самим чином, як будувався повний алгоритм в звичайному (явному) методі Рунге-Кутта п'ятого по-рядка. Єдина модифікація полягає в тому, що міри "1/4" і "1 /5", відповідна п'ятому порядку точність явної схеми, належить замінити на мірі "1/3" і "1/4", відповідна четвертому порядку точність неявної схеми.
Необхідно також нагадати, що для "жорсткої" системи ОДР перетворити вектор Е в одне число 6, що оцінює погрішність, набагато важче, чим для звичайної системи ОДР.
6. Неявні інтерполяційні схеми
Алгоритм неявних інтерполяційних методів дослівно повторює алгоритм звичайних (явних) інтерполяційних методів. Єдина відмінність полягає в тому, що ми не використовуємо звичайну (явну) схему Рунге-Кутта другого порядку:

Ми заміняємо її на неявну схему Рунге-Кутта другого порядку:

Нагадаємо, що для цієї схеми можна використовувати два різних рецепта:
• шукати точне рішення цієї системи нелінійних рівнянь методом Ньютона;
• обмежитися лінеаризованим рівнянням, тобто зробити тільки перший крок методу Ньютона :

У будь-якому випадку доведеться вирішувати СЛР. В більшості випадків можна обійтись другим варіантом, але в дуже нестійких завданнях доведеться вдатися до першого (до речі, при цьому не доведеться сильно міняти текст програми).
Нагадаємо, що існують варіанти інтерполяційного методу з фіксованим кроком Н
і змінним порядком m
, з фіксованому порядку те і змінним кроком Н
і, нарешті, із змінними m
і Н
. Тут можна привечти тільки простий алгоритм з фіксованим H
.
Алгоритм:
Вибираємо постійний крок H
за часом (як правило слід брати H
близько 0.2). Рухаємося по траєкторії з цим кроком. Кожен окремий крок реалізується так:
Для k
= 1,2,.. виконуємо наступне:
Для чергового Nk
з набору {4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128} обчислюємо крок hk
= H/Nk
.
За допомогою цього кроку hk
знаходимо 

тут tn
= t+nhk
, n = 0.. Nk
-1
; при цьому  . Зрозуміло, тут не слід обчислювати зворотну матрицю, потрібно просто вирішувати СЛР. . Зрозуміло, тут не слід обчислювати зворотну матрицю, потрібно просто вирішувати СЛР.
Для кожного хі
по k
точок:

виконуємо поліноміальну інтерполяцію взалежності Y(X) в точку X = 0. Результат інтерполяції, отриманий на k -му етапі, означаємо   . Оцінюємо погрішність . Оцінюємо погрішність
 як як 
Перетворюємо вектор  на число на число  характеризуючи погрішність. Якщо характеризуючи погрішність. Якщо  менше замовленого менше замовленого  те вважаємо те вважаємо  і завершуємо даний крок t
→
t
+
H
. і завершуємо даний крок t
→
t
+
H
.
Перша неприємна відмінність від явного методу полягає в тому, що кожен маленький крок на hk
(великий крок H
складається з Nk
штук таких кроків) вимагає рішення СЛР.
Друга неприємна відмінність від явного методу полягає в тому, що тут набагато складніше перетворити вектор  на одне число на одне число  , оцінюючи погрішність. На жаль, рецепт цього перетворення слідує підібрати залежно від конкретного завдання, тобто від конкретних властивостей "швидких" і "повільних" змінних. , оцінюючи погрішність. На жаль, рецепт цього перетворення слідує підібрати залежно від конкретного завдання, тобто від конкретних властивостей "швидких" і "повільних" змінних.
На перший погляд, цей алгоритм приведе не просто до багатьох помилок в описі динаміки "швидких" змінних, а до помилок якісних. Дійсно, якщо рівняння для "швидкої" змінної має вигляд 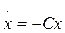 , то при Ch
>>1
неявна схема Рунге-Кутта другого порядку замість експоненціального вибуває дає x
(
t
+
h
)≈-
x
(
t
)
, тобто |
x
(
t
+
H
)|≈|
x
(
t
)|
. На щастя, наступна інтерполяція виправляє ситуацію. Інтерполяційний алгоритм "помічає", що у міру зменшення hk
абсолютна величина x
(
k
)
(
t
+
H
)
зменшується. Причому це зменшення тим помітніше, чим менше hk
- В результаті остаточна відповідь , то при Ch
>>1
неявна схема Рунге-Кутта другого порядку замість експоненціального вибуває дає x
(
t
+
h
)≈-
x
(
t
)
, тобто |
x
(
t
+
H
)|≈|
x
(
t
)|
. На щастя, наступна інтерполяція виправляє ситуацію. Інтерполяційний алгоритм "помічає", що у міру зменшення hk
абсолютна величина x
(
k
)
(
t
+
H
)
зменшується. Причому це зменшення тим помітніше, чим менше hk
- В результаті остаточна відповідь  буде помітна менше за абсолютною величиною, чим x(t). буде помітна менше за абсолютною величиною, чим x(t).
7. Програма Рунге-Кутта на мові С
#
Наведемо приклад пограми Рунге-Кутта на мові С#. В програмі використовується абстрактний клас TrungeKutta, в якому потрібно перекрити абстрактний метод F, який задає перші чаcтини рівняння.
using System;
using System.Collections.Generic;
namespace rwsh_rk4
{
abstract class TRungeKutta
{
public int N;
double t; // теперішній час
public double[] Y; // шукане число Y[0] – саме рішення, Y[i] - i-та змінна розвязку
double[] YY, Y1, Y2, Y3, Y4; // внутрішня змінна
public TRungeKutta(int N) // N – розмір системи
{
this.N = N; // зберегти розміри системи
if (N < 1)
{
this.N = -1; // якщо розмірність менше одиниці, то установити флаг помилки
return; // і вийти із конструктора
}
Y = new double[N]; // створення вектора розв’язку
YY = new double[N]; // внутрішній розв’язок
Y1 = new double[N];
Y2 = new double[N];
Y3 = new double[N];
Y4 = new double[N];
}
public void SetInit(double t0, double[] Y0) // встановлення початкових умов.
{ // t0 – початковий час, Y0 – початкова умова
t = t0;
int i;
for (i = 0; i < N; i++)
{
Y[i] = Y0[i];
}
}
public double GetCurrent() // повернути даний час
{
return t;
}
abstract public void F(double t, double[] Y, ref double[] FY); // перші частини с-ми.
public void NextStep(double dt) // наступний крок метода Рунге-Кутта, dt – крок по часу
{
if(dt<0)
{
return;
}
int i;
F(t, Y, ref Y1); // вирахувати Y1
for (i = 0; i < N; i++)
{
YY[i] = Y[i] + Y1[i] * (dt / 2.0);
}
F(t + dt / 2.0, YY, ref Y2);
for (i = 0; i < N; i++)
{
YY[i] = Y[i] + Y2[i] * (dt / 2.0);
}
F(t + dt / 2.0, YY, ref Y3); // вирахувати Y3
for (i = 0; i < N; i++)
{
YY[i] = Y[i] + Y3[i] * dt;
}
F(t + dt, YY, ref Y4); // вирахувати Y4
for (i = 0; i < N; i++)
{
Y[i] = Y[i] + dt / 6.0 * (Y1[i] + 2.0 * Y2[i] + 2.0 * Y3[i] + Y4[i]); // виразувати р-зок на новому кроці
}
t = t + dt; // збільшити крок
}
}
class TMyRK : TRungeKutta
{
public TMyRK(int aN) : base(aN) { }
public override void F(double t, double[] Y, ref double[] FY)
{
FY[0] = Y[1]; // приклад математичний маятник
FY[1] = -Y[0]; // y''(t)+y(t)=0
}
}
class Program
{
static void Main(string[] args)
{
TMyRK RK4 = new TMyRK(2);
double[] Y0 = {0, 1}; // задаємо початкові умови y(0)=0, y'(0)=1
RK4.SetInit(0, Y0);
while (RK4.GetCurrent() < 10) // розв’язуєм до 10
{
Console.WriteLine("{0}\t{1}\t{2}", RK4.GetCurrent(), RK4.Y[0], RK4.Y[1]); // вивести t, y, y'
RK4.NextStep(0.01); // розв’язати на наступному кроці, крок інтегрування dt=0.01
}
}
}
}
8. Програма
Beeman
У програмі Вееman моделюється осцилятор Морза з допомогою алгоритму Бімана. Оскільки цей алгоритм не самостартуючий, то для всіх - числових значень х(, і використовується швидкісна форма алгоритму Верле.
PROGRAM Beeman І моделювання осцилятора Морза
CALL initialfx, v, aold, dt, dt2, nmax)
CALL energy(x, v, ecum, e2cum) 1 значення початкової енергії
CALL Verleg x, v, a, aold, dt, dt2) CALL energy{ x, v, ecum, e2cum) LET n = 1
DO whiie n < nmax
LET n = n + 1 1 число кроку
CALL Bceman{x, v, a, aold, dl, dl2)
І образування повної знергії після кожного кроку за часом CALL energY(x, v, ecum, e2cum) LOOP
CALL output{ ecum, e2cum, n) END
SUB initial( x, v, aold, dt, dt2, nmax) DECLARE DEF f LET х = 2 LET v = 0 LET aold = f(x)
INPUT prompt "крок по часу (c) = ": dt LET dt2 = dt" dt
INPUT prompt "тривалість = ": tmax LET nmax = tmax/dt END SUB
SUB Ver!et( x, v, a, aold, dt, dt2) DECLARE DEF f
LET x = x + v*dt + 0.5*ao!d*dt2 LET a = f(x)
LET v = v + 0.5"{a + ao!d)*dt END SUB
SUB Beeman(x, v, a, aold, dt, dt2) DECLARE DEF f
LET x = x + v*dt + (4*a - aold)*dt2/6
LET anew = f(x) І значення на (п+1) -му кроці LET v = v + (2*anew + 5*a - aold)*dt/6
LET aold = a значення на (n-1) -му кроці
LET а = anew значення на n-му кроці END SUB
DEF f(x) LET e = exp(- x) LET f = 2*e*(e - 1) END DEF
SUB energY(x, v, ecum, e2cuin) LET KE = 0.5*v" v LET e = exp(- x) LET PE = e*{e - 2) LET etot = KE + PE LET ecum = ecum + etot LET e2cum = e2cum + etot*etot END SUB
SUB output{ecum, e2cuiT!, n) LET n = n + 1 І вирахування початкового значення
LET ebar = ecum/n PRINT "середня енергія = ";ebar LET sigma2 = e2cum/n - ebar*ebar PRINT "sigma = "; sqr(sigma2) END SUB
Метод Адамса
Цей метод чисельного інтегрування розроблений Адамсом в 1855 році на прохання видомого англійського алтелериста Башфора, який займався внутрішньою балістикою. В подальшому цей метод був забутий і знову відкритий був норвезьким математиком Штермером. Популяризація метода Адамса і подальше його вдосконалення пов’язане із іменем Крилова.
Запишемо рівняння першого порядку
З початковими умовами  (1,2)
(1,2)
Нехай xi
(
i
=0,1,2…)-
система рівнозначних значень з кроком h
i y(xi
). Очевидно маємо
 (3) (3)
В силу другої інтерполяційної формули Ньютона з точністб до різниць четвертого порядку отримуємо:
 (4) (4)
де  або або  (4а) (4а)
Підставляю вираз (4а) в формулу (3) і враховуючи те, що  будемо мати будемо мати

З відси отримуємо формулу експоляриціональну Адамса
 (5) (5)
Для початкового процессу потрібно чотири початкових значення y0,
y1,
y2
, y3,
- початковий відрізок, який приділяє, виходячи із початкових умов (2), яким-небуть чисельним методом. Мажна наприклад використати метод Рунге-Кутта або розкласти в ряд Тейлора

Де i
=1,2,3 (або
i
=-1,1,2)
із відповідною зміною нумерування. Знаючи ці значення, із рівнянь (1) можна знайти значення похідних  і скласти таблицю і скласти таблицю
 (6) (6)
Подальше значення yi
(
i
=4,5…)
шуканого розвязку можна крок за кроком обчислювати за формулою Адамса, поповнюючи по мірі можливості таблицю різниць (6)
Вирахувавши перше наближення для  по формулі по формулі

Визначити  підрахувати кінцеві різниці підрахувати кінцеві різниці
 (7) (7)
а потім знайти друге наближення для більш точній формулі
 (8) (8)
 
 Якщо Якщо  і і  відрізняються лишень на дкілька одиниць останнього зберігаючого десяткового розряду, то можна поставити відрізняються лишень на дкілька одиниць останнього зберігаючого десяткового розряду, то можна поставити  а потім знайшовши а потім знайшовши  перерахувавши кінцеві різниці (7). Після цього, потрібно знову знайти перерахувавши кінцеві різниці (7). Після цього, потрібно знову знайти  по формулі (8) Поту цей крок h
повинен бути таким, щоб цей перерахунок був зміненим. по формулі (8) Поту цей крок h
повинен бути таким, щоб цей перерахунок був зміненим.
На практиці крок h
вибирають малим, щоб можна було знехтувати членом  в формулі (8) в формулі (8)
Якщо за розбіжність величин  і і  суттєва, то потрібно зменшити крок h
. суттєва, то потрібно зменшити крок h
.
Звичайно крок h
зменшують рівно в 2 рази. Можна показати, як в цьому випадку, маючи до деякого значення і
таблицю величин х
j
,
yj
,
Yj
=
hy
’
j
(
j
<=
i
)
з кроком  , можна просто побудувати таблицю величин , можна просто побудувати таблицю величин  з кроком з кроком 
На основі формули (4) будемо мати
 (9) (9)
Де  Звідси, Звідси, 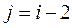 і і  і враховуючи, що і враховуючи, що  заходимо заходимо
 (10) (10)
Аналогічно при  із формули (9) отримаєм, що аргументу із формули (9) отримаєм, що аргументу  відповідає значення відповідає значення
 (11) (11)
Що стосується значень Yi
-1
i Yi
, то вони знаходяться в старій таблиці. Після цього складаємо початковий відрізок для нової таблиці:

і знаходимо кінцеві різниці:
   
Далі таблиця будується простим способом, подальшою модифікацією формули (5):

Для роботи на компютерах формулу Адамса (5) вигідно використовувати в розкритому виді. Враховуючи, що
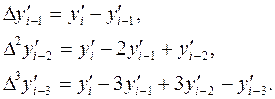
Після цього маємо:  причому причому 

Метод Крилова
Для спрощеня запису обмежимось розглядом диференціальних рівнянь першого порядка
 (1) (1)
З початковими умовами 
Введемо спочатку ряд допоміжних формул

В силу формули Адамса отримаємо
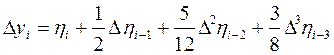 (2) (2)
Введемо позначення 
Формула (2) називається формулою
похилого
рядка
, так як в ній використовуються різниці, які знаходяться на діагоналі таблиці різниць. Враховуючи, що 
Із формули (2) будемо мати

Звідси отримуємо першу допоміжну формулу – яку ще можна назвати перша формула ламаного рядка
 (3) (3)
Далі враховуючи, що  і і  із формули (3) виводимо другу формулу – друга формула ламаного рядка із формули (3) виводимо другу формулу – друга формула ламаного рядка
 (4) (4)
Якщо  отримаємо формулу горизонтального рядка отримаємо формулу горизонтального рядка
 (5) (5)
Підмітимо, що формулу (5) можна отримати безпосередньо за допомогою інтегрування, в межах від xi
до xi
+1
розкладанням  за допомогою першої інтерполяційної формули Ньютона: за допомогою першої інтерполяційної формули Ньютона:

Перейдемо до опису метода Крилова послідовних наближень. Перше наближення полягає у тому, щоб знайти наближене значення 
 Після цього знайдемо Після цього знайдемо  і складає різницю і складає різницю  , де , де   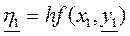 . .
Значення які знайшли заносимо в розділ (І) основного бланку (таблиця 1)
Схема обчислення відрізка методом послідовних наближень
| № наближення
|
і
|
x
|
y
|

|

|

|

|

|
| І
|
0
1
|
x0
x1
|


|

|


|

|
|
|
| ІІ
|
0
1
2
|
x0
x1
x2
|



|


|



|


|

|
|
| ІІІ
|
0
1
2
3
|
x0
x1
x2
x3
|




|



|




|
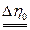


|


|

|
Далі переходимо до другого наближення. Для того, використовуємо дані із знаходження ламаних рядків, обчислюємо значення 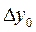 і і  : :
 (7) (7)
 (8) (8)
Двочленні формули отримуються відповідно із формули (5) при і=0
і із формули (2) при і=1
в результаті відкидання різниць порядка вищого ніж перший.
Таким чином, отримаємо можливість знайти
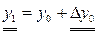 і і  , ,
в результаті чого можна порахувати

і скласти різниці

Отримані результати записуємо у таблицю в розділ 2 основного бланка
Для знаходження третього наближення застосовуємо трьохчленні формули, які отримуються із формули (2) при і=2
після відкидання різниць третього порядку. Обчислюємо значення  із трьохчленних формул: із трьохчленних формул:
 (9) (9)
 (10) (10)
 (11) (11)
Звідси можна знайти
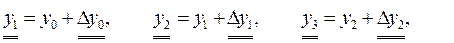
і обчислити    . Після цього можна заповнити розділ ІІІ в таблиці (І) знайшовши потрібні різниці звичайним порядком. . Після цього можна заповнити розділ ІІІ в таблиці (І) знайшовши потрібні різниці звичайним порядком.
Метод Чаплигіна
Метод Чаплигіна є одним із найбільш точним із аналітичних методів наближеного інтегрування диф. рівнянь причому допускаючи просту оцінку погрішності. Суть полягає у тому, що шуканий розв’язок  апроксимуючись двома послідовними функціями апроксимуючись двома послідовними функціями
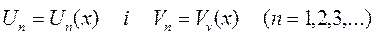
задовольняючи подвійну нерівність

і початковими умовами  причому такими, що причому такими, що  на на  при при  . Геометрично це означає, що шукана інтегральна крива . Геометрично це означає, що шукана інтегральна крива  стискається в як завгодно малий криволінійний сектор А0
Вn
Cn
(мал. 1). стискається в як завгодно малий криволінійний сектор А0
Вn
Cn
(мал. 1).
 Якщо положити Якщо положити  то максимальна абсолютна погрішність наближеного розв’язку то максимальна абсолютна погрішність наближеного розв’язку  буде рівна буде рівна   ця погрішність на кожному кроці визначається безпосередньо. ця погрішність на кожному кроці визначається безпосередньо.
Покажемо ідею метода Чаплигіна для диф. рівнянь першого порядку
 (1) (1)
з початковою умовою
 (2) (2)
Причому будемо мати на увазі, що права частина  непереривна і має неперервні похідні непереривна і має неперервні похідні 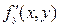 і і  в деякому околі початкової точки в деякому околі початкової точки  . Метод побудований на одній лемі. . Метод побудований на одній лемі.
Лема Чаплигіна про інтегральні нерівності
.
Нехай
 - диференціальний оператор, який відповідає диференціальному рівнянню (1), і - диференціальний оператор, який відповідає диференціальному рівнянню (1), і
 інтеграл рівняння (1)
інтеграл рівняння (1)
 (3) (3)
яке задовольняє початкову умову
 і вибраний при
і вибраний при
 .
.
Якщо функція
 задовольняючи умови:
задовольняючи умови:
 (4)
(4)
і

то на відрізку
 виконується нерівність
виконується нерівність
 (5)
(5)
так чи однаке функція і являється наближеним розв’язком
 .
.
Аналогічно і для функції
 виконуються умови:
виконуються умови:
 (6)
(6)

то на відрізку
 має місце нерівність
має місце нерівність
 , (7)
, (7)
так чи однаке функція
 являється верхнім наближеним розв’язком
являється верхнім наближеним розв’язком
 у.
у.
Доведення:
Достатньо доказати лиш одне із нерівностей (5) або (7). Доведемо наприклад нерівність (5). Із формул (3) і (4) маємо  і і  Звіди Звіди
 (8) (8)
Де
 (9) (9)
Функція  втрачає зміст при х
, для якого втрачає зміст при х
, для якого  . В цьому випадку . В цьому випадку

В силу наведених вище умов функція р(х)
визначена і неперервна на відрізку  . .
Помножимо обидві частини диференціальної нерівності (8) на інтегруючий множник  будемо мати будемо мати
 (10) (10)
Звідси інтегруючи нерівність (10) в межах від  до до  , де , де  отримаєм отримаєм  , або так як , або так як  то остаточно знаходимо то остаточно знаходимо  при при  , що і потрібно було довести. , що і потрібно було довести.
194-Чисельні методи
Висновок:
Недоліком деяких з алгоритмів, яквляється те, що деякі з них не мають амостарту, і необхідно використовувати другий алгоритм для отримання кількох пешрих точок фазовоо простору. Недоліком алгоритму Верле полягає в тому, що нова швидкість знаходиться по формулі вираховуванням близьких по величині чисел. Така операція обумовлює втрату значущих цифр і може привести до значного збільшеня погрішності округлення.
Як вже підкреслювалося, не слід віддавати перевагу одному якому-небудь алгоритму. Успіхи в комп'ютерній технології нині дозволяють легко експерементувати з різними алгоритмами для разнообразних динамічних систем.
Список використаної літератури:
1) Х. Гулд, Я.Тобочник. Компьютерное моделирование в физике: часть1.
2) В.А.Ильина, П.К. Силаев. Численные методы для физиков-теоретиков часть2. Москва, Ижевск 2004р.
3) сайт http://uk.wikipedia.org/wiki/Метод_Рунге_—_Кутти
4) И.С. Березин, Н.П. Жидков. Методы вычислений том. 2 Москва 1959р.
5) Б.П. Демидович,И.А.Марон, З.Шувалова. Численные методы анализа. «Наука» Москва 1967р.
|