Теплоемкость
Теплоемкость есть свойство вещества, характеризующее отношение количества тепла, сообщенного этому веществу, к вызванному им изменению температуры. Согласно более строгому определению, теплоемкость - термодинамическая величина, определяемая выражением
 ,(3.1) ,(3.1)
где  - количество теплоты, сообщенное системе и вызвавшее изменение ее температуры на - количество теплоты, сообщенное системе и вызвавшее изменение ее температуры на  . .
Знание теплоемкости необходимо для выполнения самых разнообразных расчетов, например, при расчете тепловых балансов, при проектировании всевозможной теплообменной аппаратуры и реакторов, при расчете химического равновесия и пр. Знание температурной зависимости теплоемкости необходимо при определении энтропии вещества, изучение теплоемкости вещества несет важную информацию о строении его молекул и пр.
При практических расчетах используются следующие понятия:
· средняя теплоемкость - это отношение конечных разностей  ; ;
· истинная теплоемкость - это отношение бесконечно малых величин  ; ;
· теплоемкость при постоянном объеме - соответствует процессу подвода тепла при постоянном объеме, когда не совершается работа расширения и количество тепла соответствует изменению внутренней энергии
 ; (3.2) ; (3.2)
· теплоемкость при постоянном давлении
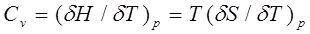 (3.3) (3.3)
соответствует процессу подвода тепла при постоянном давлении, когда повышение температуры приводит к изменению объема и, таким образом, одновременно совершается некоторая работа расширения 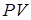 . Поскольку при изобарическом нагревании часть тепла помимо увеличения внутренней энергии идет на работу расширения, то . Поскольку при изобарическом нагревании часть тепла помимо увеличения внутренней энергии идет на работу расширения, то  . .
Для идеального газа
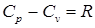 ,(3.4) ,(3.4)
где R – газовая постоянная.
На величину теплоемкости влияет природа вещества. Так, газы со сходным строением молекул имеют близкие значения теплоемкостей. С усложнением строения молекул теплоемкость, как правило, возрастает. Повышение температуры также обычно приводит к росту теплоемкости. Температурную зависимость теплоемкости нельзя получить на основе законов термодинамики, ее определяют опытным путем. Зависимость теплоемкости от температуры имеет достаточно сложный вид, для описания ее в относительно узком интервале температур в большинстве случаев используют степенные уравнения вида
 (3.5) (3.5)
или
 . (3.6) . (3.6)
Значения коэффициентов этих уравнений для многих веществ можно найти в [6].
Влияние температуры на теплоемкость жидкости меньше, чем на теплоемкость газов. Теплоемкость твердых тел при низких температурах резко уменьшается и стремится к нулю при приближении температуры к абсолютному нулю.
Теплоемкость многоатомных газов, находящихся под небольшими давлениями, практически зависит только от температуры (у одноатомных, идеальных газов она постоянна). Теплоемкость реальных газов меняется и с температурой, и с давлением, причем с повышением температуры эффект воздействия давления уменьшается. Влияние давления велико вблизи кривой насыщения, в сверхкритической и особенно в критической области, так как в критической точке значение Cv
проходит через максимум, а Cp
стремится к бесконечности. Влиянием давления на теплоемкость твердых тел можно пренебречь. Теплоемкость жидкостей с давлением меняется незначительно; только вблизи кривой насыщения и более всего в критической области влияние давления становится существенным.
Экспериментальное определение теплоемкости обычно проводят при постоянном давлении, и потому в справочной литературе чаще приводятся значения Cр
. В практике химических расчетов также чаще используются теплоемкости при постоянном давлении, поэтому в “Пособии” нами рассмотрены методы их прогнозирования. Ниже приведены методы прогнозирования теплоемкости при постоянном давлении, равном стандартному (1 физическая атмосфера) - 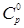 . .
При оценочных расчетах можно считать, что для большинства жидкостей их удельная теплоемкость лежит в пределах от 1,7 Дж/(г×К) до 2,5 Дж/(г×К). Исключение составляют H2
O и NH3
, для которых удельная теплоемкость равна примерно 4 Дж/(г×К), а также многие галогенпроизводные органических соединений, для которых удельная теплоемкость составляет 0,6–1,5 Дж/(г×К). Теплоемкость насыщенного пара при сравнительно небольших давлениях можно принять равной 2/3 от теплоемкости жидкости. Теплоемкость веществ, находящихся в твердом состоянии (при температурах не очень низких), можно считать примерно в 2 раза большей теплоемкости того же вещества в газообразном состоянии.
3.1. Расчет теплоемкости органических веществ
методом Бенсона [5-7, 17-18]
В табл. 1.2 приведены значения групповых вкладов для расчета теплоемкостей веществ, находящихся в состоянии идеального газа, при температурах, кратных 100 К. Расчет 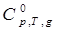 при указанных температурах выполняется аналогично прогнозированию энтальпии образования и энтропии соединений путем суммирования парциальных вкладов схемы Бенсона и введением соответствующих поправок. В отличие от энтропии при расчете теплоемкости веществ используются только те поправки, которые приведены в табл. 1.2. При расчете теплоемкости следует иметь в виду, что таблица Бенсона составлена таким образом, что для каждого из парциальных вкладов в соседних столбцах корректной является линейная интерполяция. Последний прием используется при вычислении теплоемкостей веществ, находящихся при температурах, которые не кратны 100 К. при указанных температурах выполняется аналогично прогнозированию энтальпии образования и энтропии соединений путем суммирования парциальных вкладов схемы Бенсона и введением соответствующих поправок. В отличие от энтропии при расчете теплоемкости веществ используются только те поправки, которые приведены в табл. 1.2. При расчете теплоемкости следует иметь в виду, что таблица Бенсона составлена таким образом, что для каждого из парциальных вкладов в соседних столбцах корректной является линейная интерполяция. Последний прием используется при вычислении теплоемкостей веществ, находящихся при температурах, которые не кратны 100 К.
Расчет теплоемкости методом Бенсона иллюстрируется примером 3.1.
Пример 3.1
Методом Бенсона рассчитать теплоемкость изобутилбензола в идеально-газовом состоянии (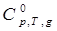 ) при 300, 400, 500, 600, 800 и 1000 К. Представить графически и аналитически температурную зависимость ) при 300, 400, 500, 600, 800 и 1000 К. Представить графически и аналитически температурную зависимость 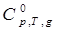 . .
Рассчитать теплоемкость 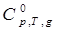 изобутилбензола при 325,0, 487,5 и 780,0 К, используя возможности метода Бенсона и результаты аппроксимации изобутилбензола при 325,0, 487,5 и 780,0 К, используя возможности метода Бенсона и результаты аппроксимации 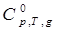 от температуры. Сопоставить полученные результаты. от температуры. Сопоставить полученные результаты.
Решение
1. Рассчитываются теплоемкости при заданных температурах. Результаты расчета для 300, 400, 500, 600 и 800 К приведены в табл. 3.1.
Температурная зависимость теплоемкости имеет нелинейный характер и иллюстрируется рис. 3.1. Там же дан вид аппроксимирующего уравнения. Из рисунка видно, что принятым в таблицах Бенсона температурным диапазонам, действительно, свойственен близкий к линейному вид для температурных зависимостей теплоемкости.
2. Вычисляется теплоемкость при заданных температурах.
T = 325,0 K
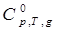 = (228,7–174,25)/100×25+174,25 = 187,9 Дж/(моль×К); = (228,7–174,25)/100×25+174,25 = 187,9 Дж/(моль×К);
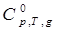 = –0,0003×3252
+0,7339×325–17,615 = 189,2 Дж/(моль×К); = –0,0003×3252
+0,7339×325–17,615 = 189,2 Дж/(моль×К);
Расхождение в оценках: (189,2–187,9)/187,9×100 = 0,7 % отн.
T = 487,5 K
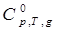 = (277,15-228,7)/100×87,5+228,7 = 271,1 Дж/(моль×К); = (277,15-228,7)/100×87,5+228,7 = 271,1 Дж/(моль×К);
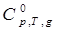 = –0,0003×487,52
+0,7339×487,5–17,615 = 268,9 Дж/(моль×К); = –0,0003×487,52
+0,7339×487,5–17,615 = 268,9 Дж/(моль×К);
Расхождение в оценках: -0,8 % отн.
T = 780,0 K
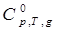 = (374,63–315,16)/200×180+315,16 = 368,7 Дж/(моль×К); = (374,63–315,16)/200×180+315,16 = 368,7 Дж/(моль×К);
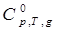 = –0,0003×7802
+ 0,7339×780–17,615 = 372,3 Дж/(моль×К). = –0,0003×7802
+ 0,7339×780–17,615 = 372,3 Дж/(моль×К).
Расхождение в оценках: 1 % отн.
Таблица 3.1
Тип атома
или группы
|
Кол-во |
Теплоемкость в Дж/(моль·К) при температуре, К |
| 300 |
400 |
500 |
600 |
800 |
| Парц. вклад |
 |
Парц. вклад |
 |
Парц. вклад |
 |
Парц. вклад |
 |
Парц. вклад |
 |
| CH3–(C) |
2 |
25,91 |
51,82 |
32,82 |
65,64 |
39,95 |
79,9 |
45,17 |
90,34 |
54,5 |
90,34 |
| CH–(3C) |
1 |
19,00 |
19,00 |
25,12 |
25,12 |
30,01 |
30,01 |
33,7 |
33,7 |
38,97 |
38,97 |
| CH2–(С,Cb) |
1 |
24,45 |
24,45 |
31,85 |
31,85 |
37,59 |
37,59 |
41,9 |
41,9 |
48,1 |
48,1 |
| Cb-(H) |
5 |
13,56 |
67,80 |
18,59 |
92,95 |
22,85 |
114,25 |
26,37 |
131,85 |
31,56 |
157,8 |
| Cb–(C) |
1 |
11,18 |
11,18 |
13,14 |
13,14 |
15,4 |
15,40 |
17,37 |
17,37 |
20,76 |
20,76 |
| |
10 |
174,25 |
228,7 |
277,15 |
315,16 |
374,63 |

Рис. 3.1. Температурная зависимость идеально-газовой теплоемкости изобутилбензола
Таким образом, прогнозирование теплоемкости при температурах, которые не кратны 100 К, может практически с равным успехом осуществляться как линейной интерполяцией “соседних” значений теплоемкостей при температурах, кратных 100 К, так и на основе аппроксимирующего их уравнения.
3.2. Теплоемкость органических веществ,
находящихся при повышенных давлениях [6]
Экспериментальные сведения о теплоемкости при высоких давлениях являются ограниченными. Поэтому прогнозирование теплоемкости оказывается неизбежным в большинстве практических расчетов. Поскольку речь идет о свойстве веществ в реальном состоянии, методы прогнозирования основаны на принципе соответственных состояний. При массовых расчетах широко используется подход, основанный на разложении Питцера, которое для теплоемкости принимает вид
 ,(3.7) ,(3.7)
где w - ацентрический фактор,
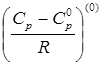 - поправка к теплоемкости на давление, характеризующая поведение простого вещества, - поправка к теплоемкости на давление, характеризующая поведение простого вещества,
 - функция отклонения в поведении рассматриваемого вещества от поведения простого вещества, - функция отклонения в поведении рассматриваемого вещества от поведения простого вещества,
 - идеально-газовая теплоемкость вещества при рассматриваемой температуре, - идеально-газовая теплоемкость вещества при рассматриваемой температуре,
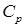 - искомая теплоемкость, - искомая теплоемкость,
R - газовая постоянная, равная 8,31441 Дж/(моль×К), или 1,98725 кал/(моль×К).
Значения 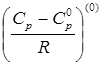 и и  представлены в таблицах Ли-Кеслера (табл. 3.2-3.3) как функции приведенной температуры и давления. Таблицы Ли-Кеслера составлены на основе уравнения состояния Бенедикта-Уэбба-Рубина с соблюдением общепринятых принципов, т.е. между любыми соседними значениями в столбцах или строках таблицы корректной является линейная интерполяция. В таблицах область, лежащая выше линии бинодали (в таблицах это жирная ломаная линия), принадлежит жидкому состоянию вещества, ниже - газообразному состоянию. представлены в таблицах Ли-Кеслера (табл. 3.2-3.3) как функции приведенной температуры и давления. Таблицы Ли-Кеслера составлены на основе уравнения состояния Бенедикта-Уэбба-Рубина с соблюдением общепринятых принципов, т.е. между любыми соседними значениями в столбцах или строках таблицы корректной является линейная интерполяция. В таблицах область, лежащая выше линии бинодали (в таблицах это жирная ломаная линия), принадлежит жидкому состоянию вещества, ниже - газообразному состоянию.
Расчет теплоемкости иллюстрируется примером 3.2.
Пример 3.2
Рассчитать теплоемкость (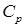 ) изобутилбензола при давлении, изменяющемся от 0,31 до 150 атм, и при температурах 325,0, 487,5 и 780,0 К. Дать графическую зависимость изотерм и выполнить их анализ. Указать фазовые состояния изобутилбензола при рассматриваемых параметрах. Критические температура, давление и ацентрический фактор изобутилбензола равны: 650 К, 31 атм и 0,378. ) изобутилбензола при давлении, изменяющемся от 0,31 до 150 атм, и при температурах 325,0, 487,5 и 780,0 К. Дать графическую зависимость изотерм и выполнить их анализ. Указать фазовые состояния изобутилбензола при рассматриваемых параметрах. Критические температура, давление и ацентрический фактор изобутилбензола равны: 650 К, 31 атм и 0,378.
Изотермические изменения теплоемкости, рассчитанные по уравнению
Значения для простого вещества 
| Tr |
Pr |
| 0,010 |
0,050 |
0,100 |
0,200 |
0,400 |
0,600 |
0,800 |
| 0,30 |
2,805 |
2,807 |
2,809 |
2,814 |
2,830 |
2,842 |
2,854 |
| 0,35 |
2,808 |
2,810 |
2,812 |
2,815 |
2,823 |
2,835 |
2,844 |
| 0,40 |
2,925 |
2,926 |
2,928 |
2,933 |
2,935 |
2,940 |
2,945 |
| 0,45 |
2,989 |
2,990 |
2,990 |
2,991 |
2,993 |
2,995 |
2,997 |
| 0,50 |
3,006 |
3,005 |
3,004 |
3,003 |
3,001 |
3,000 |
2,998 |
| 0,55 |
0,118 |
3,002 |
3,000 |
2,997 |
2,990 |
2,984 |
2,978 |
| 0,60 |
0,089 |
3,009 |
3,006 |
2,999 |
2,986 |
2,974 |
2,963 |
| 0,65 |
0,069 |
0,387 |
3,047 |
3,036 |
3,014 |
2,993 |
2,973 |
| 0,70 |
0,054 |
0,298 |
0,687 |
3,138 |
3,099 |
3,065 |
3,033 |
| 0,75 |
0,044 |
0,236 |
0,526 |
3,351 |
3,284 |
3,225 |
3,171 |
| 0,80 |
0,036 |
0,191 |
0,415 |
1,032 |
3,647 |
3,537 |
3,440 |
| 0,85 |
0,030 |
0,157 |
0,336 |
0,794 |
4,404 |
4,158 |
3,957 |
| 0,90 |
0,025 |
0,131 |
0,277 |
0,633 |
1,858 |
5,679 |
5,095 |
| 0,93 |
0,023 |
0,118 |
0,249 |
0,560 |
1,538 |
4,208 |
6,720 |
| 0,95 |
0,021 |
0,111 |
0,232 |
0,518 |
1,375 |
3,341 |
9,316 |
| 0,97 |
0,020 |
0,104 |
0,217 |
0,480 |
1,240 |
2,778 |
9,585 |
| 0,98 |
0,019 |
0,101 |
0,210 |
0,463 |
1,181 |
2,563 |
7,350 |
| 0,99 |
0,019 |
0,098 |
0,204 |
0,447 |
1,126 |
2,378 |
6,038 |
| 1,00 |
0,018 |
0,095 |
0,197 |
0,431 |
1,076 |
2,218 |
5,156 |
| 1,01 |
0,018 |
0,092 |
0,191 |
0,417 |
1,029 |
2,076 |
4,516 |
| 1,02 |
0,017 |
0,089 |
0,185 |
0,403 |
0,986 |
1,951 |
4,025 |
| 1,05 |
0,016 |
0,082 |
0,169 |
0,365 |
0,872 |
1,648 |
3,047 |
| 1,10 |
0,014 |
0,071 |
0,147 |
0,313 |
0,724 |
1,297 |
2,168 |
| 1,15 |
0,012 |
0,063 |
0,128 |
0,271 |
0,612 |
1,058 |
1,670 |
| 1,20 |
0,011 |
0,055 |
0,113 |
0,237 |
0,525 |
0,885 |
1,345 |
| 1,30 |
0,009 |
0,044 |
0,089 |
0,185 |
0,400 |
0,651 |
0,946 |
| 1,40 |
0,007 |
0,036 |
0,072 |
0,149 |
0,315 |
0,502 |
0,711 |
| 1,50 |
0,006 |
0,029 |
0,060 |
0,122 |
0,255 |
0,399 |
0,557 |
| 1,60 |
0,005 |
0,025 |
0,050 |
0,101 |
0,210 |
0,326 |
0,449 |
| 1,70 |
0,004 |
0,021 |
0,042 |
0,086 |
0,176 |
0,271 |
0,371 |
| 1,80 |
0,004 |
0,018 |
0,036 |
0,073 |
0,150 |
0,229 |
0,311 |
| 1,90 |
0,003 |
0,016 |
0,031 |
0,063 |
0,129 |
0,196 |
0,265 |
| 2,00 |
0,003 |
0,014 |
0,027 |
0,055 |
0,112 |
0,170 |
0,229 |
| 2,20 |
0,002 |
0,011 |
0,021 |
0,043 |
0,086 |
0,131 |
0,175 |
| 2,40 |
0,002 |
0,009 |
0,017 |
0,034 |
0,069 |
0,104 |
0,138 |
| 2,60 |
0,001 |
0,007 |
0,014 |
0,028 |
0,056 |
0,084 |
0,112 |
| 2,80 |
0,001 |
0,006 |
0,012 |
0,023 |
0,046 |
0,070 |
0,093 |
| 3,00 |
0,001 |
0,005 |
0,010 |
0,020 |
0,039 |
0,058 |
0,078 |
| 3,50 |
0,001 |
0,003 |
0,007 |
0,013 |
0,027 |
0,040 |
0,053 |
| 4,00 |
0,001 |
0,002 |
0,005 |
0,010 |
0,019 |
0,029 |
0,038 |
Таблица 3.2
состояния Ли-Кеслера
| Pr |
| 1,000 |
1,200 |
1,500 |
2,000 |
3,000 |
5,000 |
7,000 |
10,000 |
| 2,866 |
2,878 |
2,896 |
2,927 |
2,989 |
3,122 |
3,257 |
3,466 |
| 2,853 |
2,861 |
2,875 |
2,897 |
2,944 |
3,042 |
3,145 |
3,313 |
| 2,951 |
2,956 |
2,965 |
2,979 |
3,014 |
3,085 |
3,164 |
3,293 |
| 2,999 |
3,002 |
3,006 |
3,014 |
3,032 |
3,079 |
3,135 |
3,232 |
| 2,997 |
2,996 |
2,995 |
2,995 |
2,999 |
3,019 |
3,054 |
3,122 |
| 2,973 |
2,968 |
2,961 |
2,951 |
2,938 |
2,934 |
2,947 |
2,988 |
| 2,952 |
2,942 |
2,927 |
2,907 |
2,874 |
2,840 |
2,831 |
2,847 |
| 2,955 |
2,938 |
2,914 |
2,878 |
2,822 |
2,753 |
2,720 |
2,709 |
| 3,003 |
2,975 |
2,937 |
2,881 |
2,792 |
2,681 |
2,621 |
2,582 |
| 3,122 |
3,076 |
3,015 |
2,928 |
2,795 |
2,629 |
2,537 |
2,469 |
| 3,354 |
3,277 |
3,176 |
3,038 |
2,838 |
2,601 |
2,473 |
2,373 |
| 3,790 |
3,647 |
3,470 |
3,240 |
2,931 |
2,599 |
2,427 |
2,292 |
| 4,677 |
4,359 |
4,000 |
3,585 |
3,096 |
2,626 |
2,399 |
2,227 |
| 5,766 |
5,149 |
4,533 |
3,902 |
3,236 |
2,657 |
2,392 |
2,195 |
| 7,127 |
6,010 |
5,050 |
4,180 |
3,351 |
2,684 |
2,391 |
2,175 |
| 10,011 |
7,451 |
5,785 |
4,531 |
3,486 |
2,716 |
2,393 |
2,159 |
| 13,270 |
8,611 |
6,279 |
4,743 |
3,560 |
2,733 |
2,395 |
2,151 |
| 21,948 |
10,362 |
6,897 |
4,983 |
3,641 |
2,752 |
2,398 |
2,144 |
| ****** |
13,281 |
7,686 |
5,255 |
3,729 |
2,773 |
2,401 |
2,138 |
| 22,295 |
18,967 |
8,708 |
5,569 |
3,821 |
2,794 |
2,405 |
2,131 |
| 13,184 |
31,353 |
10,062 |
5,923 |
3,920 |
2,816 |
2,408 |
2,125 |
| 6,458 |
20,234 |
16,457 |
7,296 |
4,259 |
2,891 |
2,425 |
2,110 |
| 3,649 |
6,510 |
13,256 |
9,787 |
4,927 |
3,033 |
2,462 |
2,093 |
| 2,553 |
3,885 |
6,985 |
9,094 |
5,535 |
3,186 |
2,508 |
2,083 |
| 1,951 |
2,758 |
4,430 |
6,911 |
5,710 |
3,326 |
2,555 |
2,079 |
| 1,297 |
1,711 |
2,458 |
3,850 |
4,793 |
3,452 |
2,628 |
2,077 |
| 0,946 |
1,208 |
1,650 |
2,462 |
3,573 |
3,282 |
2,626 |
2,068 |
| 0,728 |
0,912 |
1,211 |
1,747 |
2,647 |
2,917 |
2,525 |
2,038 |
| 0,580 |
0,719 |
0,938 |
1,321 |
2,016 |
2,508 |
2,347 |
1,978 |
| 0,475 |
0,583 |
0,752 |
1,043 |
1,586 |
2,128 |
2,130 |
1,889 |
| 0,397 |
0,484 |
0,619 |
0,848 |
1,282 |
1,805 |
1,907 |
1,778 |
| 0,336 |
0,409 |
0,519 |
0,706 |
1,060 |
1,538 |
0,696 |
1,656 |
| 0,289 |
0,350 |
0,443 |
0,598 |
0,893 |
1,320 |
1,505 |
1,531 |
| 0,220 |
0,265 |
0,334 |
0,446 |
0,661 |
0,998 |
1,191 |
1,292 |
| 0,173 |
0,208 |
0,261 |
0,347 |
0,510 |
0,779 |
0,956 |
1,086 |
| 0,140 |
0,168 |
0,210 |
0,278 |
0,407 |
0,624 |
0,780 |
0,917 |
| 0,116 |
0,138 |
0,172 |
0,227 |
0,332 |
0,512 |
0,647 |
0,779 |
| 0,097 |
0,116 |
0,144 |
0,190 |
0,277 |
0,427 |
0,545 |
0,668 |
| 0,066 |
0,079 |
0,098 |
0,128 |
0,187 |
0,289 |
0,374 |
0,472 |
| 0,048 |
0,057 |
0,071 |
0,093 |
0,135 |
0,209 |
0,272 |
0,350 |
Изотермические изменения теплоемкости, рассчитанные по уравнению
Значения для простого вещества 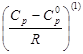
| Tr |
Pr |
| 0,010 |
0,050 |
0,100 |
0,200 |
0,400 |
0,600 |
0,800 |
| 0,30 |
8,462 |
8,445 |
8,424 |
8,381 |
8,281 |
8,192 |
8,102 |
| 0,35 |
9,775 |
9,762 |
9,746 |
9,713 |
9,646 |
9,568 |
9,499 |
| 0,40 |
11,494 |
11,484 |
11,471 |
11,438 |
11,394 |
11,343 |
11,291 |
| 0,45 |
12,651 |
12,643 |
12,633 |
12,613 |
12,573 |
12,532 |
12,492 |
| 0,50 |
13,111 |
13,106 |
13,099 |
13,084 |
13,055 |
13,025 |
12,995 |
| 0,55 |
0,511 |
13,035 |
13,030 |
13,021 |
13,002 |
12,981 |
12,961 |
| 0,60 |
0,345 |
12,679 |
12,675 |
12,668 |
12,653 |
12,637 |
12,620 |
| 0,65 |
0,242 |
1,518 |
12,148 |
12,145 |
12,137 |
12,128 |
12,117 |
| 0,70 |
0,174 |
1,026 |
2,968 |
11,557 |
11,564 |
11,563 |
11,559 |
| 0,75 |
0,129 |
0,726 |
1,747 |
10,967 |
10,995 |
11,011 |
11,019 |
| 0,80 |
0,097 |
0,532 |
1,212 |
3,511 |
10,490 |
10,536 |
10,566 |
| 0,85 |
0,075 |
0,399 |
0,879 |
2,247 |
9,999 |
10,153 |
10,245 |
| 0,90 |
0,058 |
0,306 |
0,658 |
1,563 |
5,486 |
9,793 |
10,180 |
| 0,93 |
0,050 |
0,263 |
0,560 |
1,289 |
3,890 |
****** |
10,285 |
| 0,95 |
0,046 |
0,239 |
0,505 |
1,142 |
3,215 |
9,389 |
9,993 |
| 0,97 |
0,042 |
0,217 |
0,456 |
1,018 |
2,712 |
6,588 |
****** |
| 0,98 |
0,040 |
0,207 |
0,434 |
0,962 |
2,506 |
5,711 |
****** |
| 0,99 |
0,038 |
0,198 |
0,414 |
0,911 |
2,324 |
5,027 |
****** |
| 1,00 |
0,037 |
0,189 |
0,394 |
0,863 |
2,162 |
4,477 |
10,511 |
| 1,01 |
0,035 |
0,181 |
0,376 |
0,819 |
2,016 |
4,026 |
8,437 |
| 1,02 |
0,034 |
0,173 |
0,359 |
0,778 |
1,884 |
3,648 |
7,044 |
| 1,05 |
0,030 |
0,152 |
0,313 |
0,669 |
1,559 |
2,812 |
4,679 |
| 1,10 |
0,024 |
0,123 |
0,252 |
0,528 |
1,174 |
1,968 |
2,919 |
| 1,15 |
0,020 |
0,101 |
0,205 |
0,424 |
0,910 |
1,460 |
2,048 |
| 1,20 |
0,016 |
0,083 |
0,168 |
0,345 |
0,722 |
1,123 |
1,527 |
| 1,30 |
0,012 |
0,058 |
0,116 |
0,235 |
0,476 |
0,175 |
0,938 |
| 1,40 |
0,008 |
0,042 |
0,083 |
0,166 |
0,329 |
0,484 |
0,624 |
| 1,50 |
0,006 |
0,030 |
0,061 |
0,120 |
0,235 |
0,342 |
0,437 |
| 1,60 |
0,005 |
0,023 |
0,045 |
0,089 |
0,173 |
0,249 |
0,317 |
| 1,70 |
0,003 |
0,017 |
0,034 |
0,068 |
0,130 |
0,187 |
0,236 |
| 1,80 |
0,003 |
0,013 |
0,027 |
0,052 |
0,100 |
0,143 |
0,180 |
| 1,90 |
0,002 |
0,011 |
0,021 |
0,041 |
0,078 |
0,111 |
0,140 |
| 2,00 |
0,002 |
0,008 |
0,017 |
0,032 |
0,062 |
0,088 |
0,110 |
| 2,20 |
0,001 |
0,005 |
0,011 |
0,021 |
0,040 |
0,057 |
0,072 |
| 2,40 |
0,001 |
0,004 |
0,007 |
0,014 |
0,028 |
0,039 |
0,049 |
| 2,60 |
0,001 |
0,003 |
0,005 |
0,010 |
0,020 |
0,028 |
0,035 |
| 2,80 |
0,000 |
0,002 |
0,004 |
0,008 |
0,014 |
0,021 |
0,026 |
| 3,00 |
0,000 |
0,001 |
0,003 |
0,006 |
0,011 |
0,016 |
0,020 |
| 3,50 |
0,000 |
0,001 |
0,002 |
0,003 |
0,006 |
0,009 |
0,012 |
| 4,00 |
0,000 |
0,001 |
0,001 |
0,002 |
0,004 |
0,006 |
0,008 |
Таблица 3.3
состояния Ли-Кеслера
| Pr |
| 1,000 |
1,200 |
1,500 |
2,000 |
3,000 |
5,000 |
7,000 |
10,000 |
| 8,011 |
7,920 |
7,785 |
7,558 |
7,103 |
6,270 |
5,372 |
4,020 |
| 9,430 |
9,360 |
9,256 |
9,080 |
8,728 |
8,013 |
7,290 |
6,285 |
| 11,240 |
11,188 |
11,110 |
10,980 |
10,709 |
10,170 |
9,625 |
8,803 |
| 12,451 |
12,409 |
12,347 |
12,243 |
12,029 |
11,592 |
11,183 |
10,533 |
| 12,964 |
12,933 |
12,886 |
12,805 |
12,639 |
12,288 |
11,946 |
11,419 |
| 12,939 |
12,917 |
12,882 |
12,823 |
12,695 |
12,407 |
12,103 |
11,673 |
| 12,589 |
12,574 |
12,550 |
12,506 |
12,407 |
12,165 |
11,905 |
11,526 |
| 12,105 |
12,092 |
12,060 |
12,026 |
11,943 |
11,728 |
11,494 |
11,141 |
| 11,553 |
11,536 |
11,524 |
11,495 |
11,416 |
11,208 |
10,985 |
10,661 |
| 11,024 |
11,022 |
11,013 |
10,986 |
10,898 |
10,677 |
10,448 |
10,132 |
| 10,583 |
10,590 |
10,587 |
10,556 |
10,446 |
10,176 |
9,917 |
9,591 |
| 10,297 |
10,321 |
10,324 |
10,278 |
10,111 |
9,740 |
9,433 |
9,075 |
| 10,349 |
10,409 |
10,401 |
10,279 |
9,940 |
9,389 |
8,999 |
8,592 |
| 10,769 |
10,875 |
10,801 |
10,523 |
9,965 |
9,225 |
8,766 |
8,322 |
| 11,420 |
11,607 |
11,387 |
10,865 |
10,055 |
9,136 |
8,621 |
8,152 |
| 13,001 |
****** |
12,498 |
11,445 |
10,215 |
9,061 |
8,485 |
7,986 |
| ****** |
****** |
****** |
11,856 |
10,323 |
9,037 |
8,420 |
7,905 |
| ****** |
****** |
****** |
12,388 |
10,457 |
9,011 |
8,359 |
7,826 |
| ****** |
****** |
****** |
13,081 |
10,617 |
8,990 |
8,293 |
7,747 |
| ****** |
****** |
****** |
****** |
10,805 |
8,973 |
8,236 |
7,670 |
| ****** |
****** |
****** |
****** |
11,024 |
8,960 |
8,182 |
7,595 |
| 7,173 |
2,277 |
****** |
****** |
11,852 |
8,939 |
8,018 |
7,377 |
| 3,877 |
4,002 |
3,927 |
****** |
****** |
8,933 |
7,759 |
7,031 |
| 2,587 |
2,844 |
2,236 |
7,716 |
12,812 |
8,849 |
7,504 |
6,702 |
| 1,881 |
2,095 |
1,962 |
2,965 |
9,494 |
8,508 |
7,206 |
6,384 |
| 1,129 |
1,264 |
1,327 |
1,288 |
3,855 |
6,758 |
6,365 |
5,735 |
| 0,743 |
0,833 |
0,904 |
0,905 |
1,652 |
4,524 |
5,193 |
5,035 |
| 0,517 |
0,580 |
0,639 |
0,666 |
0,907 |
2,823 |
3,944 |
4,289 |
| 0,374 |
0,419 |
0,466 |
0,499 |
0,601 |
1,755 |
2,871 |
3,545 |
| 0,278 |
0,312 |
0,349 |
0,380 |
0,439 |
1,129 |
2,060 |
2,867 |
| 0,212 |
0,238 |
0,267 |
0,296 |
0,337 |
0,764 |
1,483 |
2,287 |
| 0,164 |
0,185 |
0,209 |
0,234 |
0,267 |
0,545 |
1,085 |
1,817 |
| 0,130 |
0,146 |
0,166 |
0,187 |
0,217 |
0,407 |
0,812 |
1,466 |
| 0,085 |
0,096 |
0,110 |
0,126 |
0,150 |
0,256 |
0,492 |
0,941 |
| 0,058 |
0,066 |
0,076 |
0,089 |
0,109 |
0,180 |
0,329 |
0,644 |
| 0,042 |
0,048 |
0,056 |
0,066 |
0,084 |
0,137 |
0,239 |
0,466 |
| 0,031 |
0,036 |
0,042 |
0,051 |
0,067 |
0,110 |
0,187 |
0,356 |
| 0,024 |
0,028 |
0,033 |
0,041 |
0,055 |
0,092 |
0,153 |
0,285 |
| 0,015 |
0,017 |
0,021 |
0,026 |
0,038 |
0,067 |
0,108 |
0,190 |
| 0,010 |
0,012 |
0,015 |
0,019 |
0,029 |
0,054 |
0,085 |
0,146 |
Решение
1. Рассчитываются приведенные температуры:
 = 325/650 =0,50; = 325/650 =0,50; 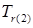 = 487,5/650 =0,75; = 487,5/650 =0,75;  = 780/650 =1,20. = 780/650 =1,20.
2. При полученных приведенных температурах и значениях приведенных давлений таблиц Ли-Кеслера вычисляются значения 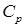 . Необходимые для расчета величины . Необходимые для расчета величины  получены в примере 3.1. Для получены в примере 3.1. Для  и и  = 0,01 имеем: = 0,01 имеем:
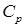 = 187,9 + 8,31441×(3,006+0,378×13,111) = 254,1 Дж/(моль×К). = 187,9 + 8,31441×(3,006+0,378×13,111) = 254,1 Дж/(моль×К).
Фрагмент результатов расчета приведен в табл. 3.4 и 3.5, где жирным шрифтом выделены сведения, относящиеся к жидкому состоянию изобутилбензола.
3. Зависимость теплоемкости от давления при избранных температурах приведена на рис. 3.2. Характер полученных графических зависимостей различен для изотерм, принадлежащих жидкому и газообразному состояниям вещества. Теплоемкость жидкости мало зависит от давления, что очевидно. Теплоемкость газа в закритической области возрастает с увеличением давления до некоторого уровня, а затем начинает падать, т.е. зависимость носит экстремальный характер. Для докритической изотермы резкое изменение теплоемкости происходит при изменении фазового состояния вещества.

Рис. 3.2. Зависимость теплоемкости изобутилбензола от давления при 325, 487,5 и 780 К
Таблица 3.4
 |

при приведенном давлении, 
|

при приведенном давлении, 
|
| 0,010 |
0,050 |
0,100 |
0,200 |
0,400 |
0,010 |
0,050 |
0,100 |
0,200 |
0,400 |
| 0,50 |
3,006 |
3,005 |
3,004 |
3,003 |
3,001 |
13,111 |
13,106 |
13,099 |
13,084 |
13,055 |
| 0,010 |
0,050 |
0,100 |
0,200 |
0,400 |
0,010 |
0,050 |
0,100 |
0,200 |
0,400 |
| 0,75 |
0,044 |
0,236 |
0,526 |
3,351 |
3,284 |
0,129 |
0,726 |
1,747 |
10,967 |
10,995 |
| 1,20 |
0,011 |
0,055 |
0,113 |
0,237 |
0,525 |
0,016 |
0,083 |
0,168 |
0,345 |
0,722 |
Таблица 3.5
| T, K |
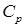 , Дж/(моль×К), при давлении, атм , Дж/(моль×К), при давлении, атм |
| 0,31 |
1,55 |
3,1 |
6,2 |
12,4 |
18,6 |
24,8 |
31 |
37,2 |
46,5 |
| 325,0 |
254,00 |
253,97 |
253,94 |
253,89 |
253,78 |
253,68 |
253,56 |
253,46 |
253,35 |
253,20 |
| 487,5 |
270,70 |
274,17 |
279,79 |
332,25 |
331,79 |
331,35 |
330,92 |
330,53 |
330,14 |
329,61 |
| 780,0 |
368,68 |
369,25 |
370,00 |
371,59 |
375,17 |
379,42 |
384,52 |
390,67 |
398,05 |
411,53 |
|