Задание № 1
В урне 5 белых и 4 черных шара. Из нее вынимают подряд два ряда шара. Найти вероятность того, что оба шара белые.
Решение:
Всего возможно 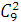 . (это общее количество возможных элементарных исходов испытания). Интересующая нас событие заключается в том, что данная выборка содержит 2 белых шара, подсчитаем число благоприятствующих этому событию вариантов: . (это общее количество возможных элементарных исходов испытания). Интересующая нас событие заключается в том, что данная выборка содержит 2 белых шара, подсчитаем число благоприятствующих этому событию вариантов: 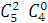
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
По формуле полной вероятности имеем:


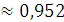
Задание № 2
Имеется 2 урны: в первой 3 белых и 4 черных шара, во второй 5 белых и 7 черных. Из наудачу выбранной урны берут один шар. Найти вероятность того, что этот шар будет белым.
Решение:
Пусть событие А сводится к тому, что шар достали (из одной из урн). Предположим, что:
1) Н1 = шар достали из урны первой
2) Н2 = шар достали из урны второй
Вероятность того, что шар достали из первой урны Р (Н1) = 1/3, а вероятность того, что шар достали из второй урны Р (Н1) = 1/5. Согласно условию задачи в случае Н1 шар достанут с вероятностью: Р (А/Н1) = 3/7, а в случае Н2 – с вероятностью Р (А/Н2) = 5/12. По формуле полной вероятности имеем:
Р (А) = Р (Н1) * Р (А/Н1) + Р (Н2) * Р (А/Н2),

Задание № 3
Дана вероятность p появления события А в серии из n независимых испытаний. Найти вероятность того, что в этих испытаниях событие А появится:
а) равно к раз;
б) не менее к раз;
в) не менее к1
раз и не более к2
раз.
Решение:
В нашем случае р = 0,3, тогда g = 1 – 0,3 = 0,7, n = 6 и к = 3, отсюда вероятность появления события в серии из 6 независимых испытаний:
а) n = 6, к = 3, р = 0,3, тогда g = 0,7. По формуле Бернуле имеем:
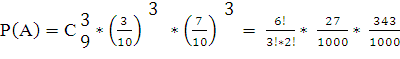 = =

б) вероятность появления события а не менее 3 раз из независимых испытаний предположим, что событие должно повторяться более 3 раз: Рn (к1;n) = Ф (в) – Ф (а),
 

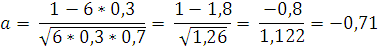
Р6 (1; 6) = Ф (3,74) – (+Ф (-0,71)) = 0,6233 + 0,2528 = 0,8761
Так как рассматриваемое событие появляется не менее 3 раз, имеем:
1 – Рn
(К1
; n) = = 1 - 0,8761 = 0,1449
в) вероятность того, что событие появится в серии из 6 независимых испытаний не менее 1 раза и не более 3 раз можно найти по Формуле Лапласа:
Рn (к1; к2) = Ф (в) – Ф (а),
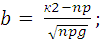 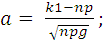

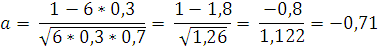
Р6 (1; 3) = Ф (1,07) – (+Ф (-0,71)) = 0,3103 + 0,2528 = 0,5631
Задание № 4
| х |
-2 |
-1 |
0 |
3 |
| р |
0,2 |
0,5 |
0,1 |
0,2 |
Таблицей задан закон распределения дискретной случайной, величины Х. Найти математическое ожидание М (х), D(х) и среднее квадратическое отклонение σ (х). Закон распределения.
Решение:
М (х) = -2 * 0.2 + (-1) * 0,5 + 0 * 0,1 + 3 * 0,2 = -0,4 – 0,5 + 0 + 0,6 = 0,5
D (х) = М (х2
) – (М (х))2
, найдем х2
;
| х |
-2 |
-1 |
0 |
3 |
| р |
0,2 |
0,5 |
0,1 |
0,2 |
М (х2
) = 4 * 0,2 + 1 * 0,5 + 0 * 0,1 + 9 * 0,2 = 0,8 + 0,5 + 0 + 1,8 = 3,1, тогда в (х) = = 3,1 + (0,5)2
= 3,1 – 0,25 = 2,85.
Среднее квадратическое отклонение:
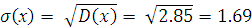
Задание № 5
Дана интегральная функция распределения случайная величина Х. Найти дифференциальную функцию распределения, математическое ожидание М (х), дисперсия в (х) и среднее квадратическое отклонение σ (х).
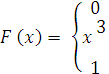 
Решение:




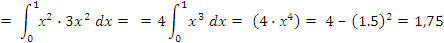
Среднее квадратическое отклонение равно:

Задание № 6
Диаметры деталей распределены по нормальному закону. Среднее значение диаметра равно в мм, среднее квадратическое отклонение σ мм. Найти вероятность того, что диаметр наудачу взятой детали будет больше, α мм и меньше β мм; вероятность того, что диаметр детали отклонится от стандартной длины не более, чем на Δ мм.
Решение:
Пусть х – длина детали. Если случайная величина х распределена по нормальному закону, то вероятность ее попадания на отрезок [а; в].


= 
Вероятность отклонения длины детали от ее математического ожидания а не больше, чем на в = 1 мм, очевидно, что есть вероятность того, что длина детали попадает в интервал [а - d; а + d] и потому вычисляется также с помощью функции Лапласа:


Задание № 7
Признак Х представлен дискретным выборочным распределением в виде таблицы выборочных значений (таблица 1). Требуется:
‾ составить интервальное распределение выборки;
‾ построить гистограмму относительных частот;
‾ перейти от составленного интервального распределения к точечному выборочному распределению, взяв за значение признака середины частичных интервалов;
‾ построить полигон относительных частот;
‾ найти эмпирическую функцию распределения и построить ее график;
‾ вычислить все точечные статистические оценки числовых характеристик признака: среднее х; выборочную дисперсию и исправленную выборочную дисперсию; выборочное среднее квадратическое отклонение и исправленное среднее квадратическое отклонение S;
‾ считая первый столбец таблицы 1 выборкой значений признака X, а второй столбец выборкой значений Y, оценить тесноту линейной корреляционной зависимости между признаками и составить выборочное уравнение прямой регрессии Y на X.
Таблица 1 Таблица выборочных значений
| 66,7 |
70,5 |
57,5 |
58,5 |
74,7 |
75,8 |
99,9 |
58,5 |
93,0 |
74,8 |
| 26,7 |
37,5 |
61,5 |
38,0 |
62,5 |
60,5 |
59,0 |
71,5 |
65,5 |
65,2 |
| 91,5 |
79,5 |
31,8 |
71,5 |
63,0 |
69,5 |
79,3 |
95,0 |
83,5 |
51,0 |
| 66,4 |
65,3 |
66,2 |
85,5 |
46,5 |
48,5 |
36,9 |
68,5 |
86,9 |
73,7 |
| 40,3 |
66,5 |
87,7 |
39,5 |
64,3 |
63,9 |
67,3 |
94,8 |
43,5 |
73,1 |
| 67,8 |
75,1 |
44,9 |
58,9 |
70,9 |
68,2 |
65,3 |
65,9 |
74,0 |
63,9 |
| 50,0 |
66,5 |
43,5 |
56,2 |
74,0 |
64,3 |
34,9 |
52,1 |
44,9 |
54,1 |
| 66,0 |
43,2 |
70,5 |
85,1 |
45,8 |
79,2 |
47,7 |
60,3 |
60,5 |
85,6 |
| 362,8 |
93,2 |
53,6 |
85,7 |
55,8 |
46,5 |
59,5 |
62,6 |
92,8 |
79,5 |
| 46,5 |
60,3 |
81,3 |
38,5 |
55,3 |
58,8 |
81,3 |
57,5 |
34,3 |
46,5 |
Решение:
1) определим максимальное и минимальное значение имеющихся значений: хmin
= 26,7 хmax
= 99,9
2) Выстроим в порядке возрастания, имеющиеся у нас значения (табл.2)
Таблица 2
| 26,7 |
31,8 |
34,3 |
34,9 |
36,9 |
37,5 |
38,0 |
38,5 |
39,5 |
40,3 |
43,2 |
| 43,5 |
43,5 |
44,9 |
44,9 |
45,8 |
46,5 |
46,5 |
46,5 |
46,5 |
47,7 |
48,5 |
| 50,0 |
51,0 |
52,1 |
53,6 |
54,1 |
55,3 |
55,8 |
56,2 |
57,5 |
57,5 |
58,5 |
| 58,5 |
58,8 |
58,9 |
59,0 |
59,5 |
60,3 |
60,3 |
60,5 |
60,5 |
61,5 |
62,5 |
| 62,6 |
62,8 |
63,0 |
63,9 |
63,9 |
64,3 |
64,3 |
65,2 |
65,3 |
65,3 |
65,5 |
| 65,9 |
66,0 |
66,2 |
66,4 |
66,5 |
66,5 |
66,7 |
67,3 |
67,8 |
68,2 |
68,5 |
| 69,5 |
70,5 |
70,5 |
70,9 |
71,5 |
73,1 |
73,7 |
74,0 |
74,0 |
74,7 |
74,8 |
| 75,1 |
75,8 |
79,2 |
79,3 |
79,3 |
79,5 |
81,3 |
81,3 |
83,5 |
85,1 |
85,5 |
| 85,6 |
85,7 |
86,9 |
87,7 |
91,5 |
92,8 |
93,0 |
93,2 |
94,8 |
95,0 |
99,9 |
3) Определим размах R: R = хmax
- хmin
= 99,9 - 26,7 = 73,2

Нижняя граница х0
= хmin
– L / 2 = 26,7 – 10 / 2 = 21,7;
Верхняя граница хi
= хmax
+ L / 2 = 99.9 + 10 / 2 = 104,9,
следовательно, у нас имеются интервалы: [21,7; 31,7); [31,7; 41,7); [41,7; 51,7); [51,7; 61,7); [61,7; 71,7); [71,7; 81,7); [81,7; 91,7); [91,7; 104,7].
5) wi = ni / n
| х 1-i x i |
[21,7;
31,7)
|
[31,7;
41,7)
|
[41,7;
51,7)
|
[51,7;
61,7)
|
[61,7;
71,7)
|
[71,7;
81,7)
|
[81,7;
91,7)
|
[91,7;
104,7]
|
| ni |
1 |
9 |
14 |
19 |
29 |
14 |
8 |
6 |
| wi |
0,01 |
0,09 |
0,14 |
0,19 |
0,29 |
0,14 |
0,08 |
0,06 |
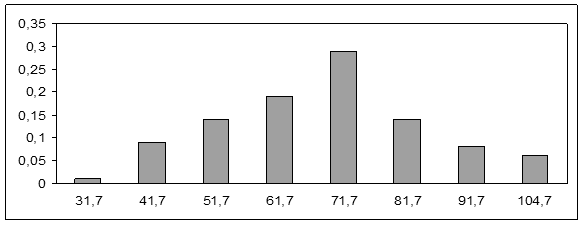
Рис. 1. Гистограмма относительных частот
Перейдем от составленного интервального распределения к точечному выборочному распределению, взяв за значение признака середины частичных интервалов. Построим полигон относительных частот и найдем эмпирическую функцию распределения, построим ее график:
| x i |
26,7 |
36,7 |
46,7 |
56,7 |
66,7 |
76,7 |
86,7 |
98,3 |
| ni |
1 |
9 |
14 |
19 |
29 |
14 |
8 |
6 |
| wi |
0,01 |
0,09 |
0,14 |
0,19 |
0,29 |
0,14 |
0,08 |
0,06 |

Рис. 2. График интервального распределения.



Рис. 3. График эмпирической функции распределения
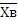 =
=  ∑ xi
wi
= ∑ xi
wi ∑ xi
wi
= ∑ xi
wi
∑ xi
wi
= 26,7 * 0,01 + 36,7 * 0,09 + 46,7 * 0,14 + 56,7 * 0,19 + 66,7 * 0,29 + 76,7 * 0,14 + 86,7 *0,08 + 98,3 * 0,06 =26,71 + 3, 303 + 6,538 + 10,773 +
+ 19,343 + 10,738 + 6,936 + 5,898 = 90,2
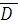 = ∑ = ∑ = = (26,7 – 90,2)2
* 0,01 +(36,7 – 90,2) 2
*0,09 + (46,7 – 90,2) 2
* 0,14 + (56,7 – 90,2) 2
* 0,19 + (66,7 – 90,2) 2
* 0,29 + (76,7 – 90,2) 2
*0,14 + (86,7 – 90,2) 2
* 0,08 + (98,3 – 90,2) 2
* 0,06 = 40,32 + 257,6 + 264,92 +213,23 + 160,15 + 25,52 + 0,98 + 3,94 = 966,66 = = (26,7 – 90,2)2
* 0,01 +(36,7 – 90,2) 2
*0,09 + (46,7 – 90,2) 2
* 0,14 + (56,7 – 90,2) 2
* 0,19 + (66,7 – 90,2) 2
* 0,29 + (76,7 – 90,2) 2
*0,14 + (86,7 – 90,2) 2
* 0,08 + (98,3 – 90,2) 2
* 0,06 = 40,32 + 257,6 + 264,92 +213,23 + 160,15 + 25,52 + 0,98 + 3,94 = 966,66


Задание № 8
Даны среднее квадратическое отклонение σ, выборочное среднее  и объем выборки nнормального распределенного признака генеральной совокупности. Найти доверительные интервалы для оценки генеральной средней и объем выборки nнормального распределенного признака генеральной совокупности. Найти доверительные интервалы для оценки генеральной средней 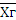 с заданной надежностью γ. с заданной надежностью γ.
| σ |
 |
n |
γ |
| 7 |
112,4 |
26 |
0,95 |
Решение:
Доверительный интервал, в котором с вероятностью γ будет находиться средний интервал совокупности) для нормального распределения случайной величины с известным квадратичным отклонением σ, выборочной средней  и объемом выборки n равен. и объемом выборки n равен.

t – решение уравнения 2Ф (t) = γ, Ф (t) – функция Лапласа. В нашем случае Ф (t) =  = 0,475, следовательно, значение Ф (t) соответствует t = 2,13, тогда доверительный интервал будет равен: = 0,475, следовательно, значение Ф (t) соответствует t = 2,13, тогда доверительный интервал будет равен:

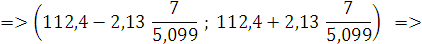
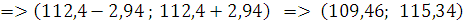 . .
В этом интервале с вероятностью γ = 0,95, будет находиться средняя генеральной совокупности.
Задание № 9
Даны исправленное среднее квадратическое отклонение S, выборочное среднее  и объем выборки n нормально распределенного признака генеральной совокупности. Пользуясь распределением Стьюдента, найти доверительные интервалы для оценки генеральной средней и объем выборки n нормально распределенного признака генеральной совокупности. Пользуясь распределением Стьюдента, найти доверительные интервалы для оценки генеральной средней 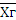 , с заданной надежностью γ. , с заданной надежностью γ.
| S |
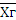 |
n |
γ |
| 13 |
119.5 |
18 |
0,99 |
Решение:
Доверительный интервал, для нормального распределения случайной величины с известным квадратичным отклонением σ, но с известным исправленным средним квадратичным отклонением S, выборочной средней  и объемом выборки n и доверительной вероятностью γ, имеет вид. и объемом выборки n и доверительной вероятностью γ, имеет вид.

где tγ
= t (γ; n) – коэффициенты Стьюдента, значения n = 18 и γ = 0,99, tγ
= 2,39, то есть t (0,99; 18) = 2,39.
Тогда доверительный интервал:
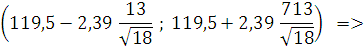

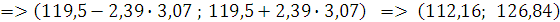
В интервале (112,16; 126,84) с вероятностью γ = 0,99 будет находиться средняя генеральной совокупности.
Задание № 10
При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты.
| эмпирические частоты, ni |
3 |
13 |
17 |
45 |
13 |
14 |
5 |
| теоретические частоты, n’i |
5 |
15 |
14 |
50 |
11 |
12 |
3 |
Решение:
В соответствии с критерием согласия х 2
(Пирсона) определим наблюдаемое значение критерия:




Таким образом, Хо
2
= 2,91, по таблице критических точек распределения при уровне значимости в = 0,05 и числе степени свободы к = m – 3 = 7 – 3 = 4, где m – число различных вариантов выборки, находим: Хкр
2
.
Хкр
2
= х2
(0,05; 4) = 8,0
Так как Хо
2
<Хкр
2
, то нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности.
|