Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Государственный университет управления
Кафедра статистики
Семестровое домашнее задание
по статистике
Раздел «Общая теория статистики»
| Выполнил |
Проверил |
Студент II курса ИМ
2 курс, вечернее отделение
Герасимов Г. Н.
Вариант № 6-45
|
Доцент кафедры статистики
канд. экон. наук
СИЛЬЧЕНКО Александр Семенович
Итоговая оценка
__________________________
__________________________
|
Москва, 2008
ЗАДАНИЯ:
1. Произвести группировку предприятий
по стоимости основных производственных фондов в отчетном году
с целью выявления зависимости между
размером предприятия по стоимости основных производственных фондов и
физическим объемом выработанной продукции.
Результаты представить в виде статистической таблицы, сформулировать выводы.
2. Построить ряд распределения
предприятий по физическому объему выпущенной продукции в отчетном году, рассчитав величину интервала по формуле Стерджесса.
Для построенного ряда определить среднюю арифметическую величину, моду, медиану, показатели вариации, показатель ассимстрии.
По правилу 3-х сигм проверить соответствие эмпирического распределения нормальному, сформулировать выводы.
3. Используя ранее выполненную группировку предприятий по стоимости основных фондов, (п.1), проверить правило сложения дисперсий
по физическому объему выпущенной продукции.
4. Предприятия, по которым имеются отчетные данные, представляют собой десятипроцентную простую случайную выборку из общего числа предприятий данной отрасли.
Требуется определить:
а) среднюю стоимость основных производственных фондов для всех предприятий отрасли в отчетном году, гарантируя результат с вероятностью 0,997;
б) вероятность того, что средняя стоимость основных производственных фондов отличается от полученной по выборке не более, чем на 1,0млн.руб. (на 10% от выборочной средней).
5. Рассчитав индексы цен Пааше, Ласперса и Фишера. Проанализировать полученные результаты.
6. Определить прирост стоимости произведенной продукции за счет выпуска экспорта в каждом году.
ИСХОДНЫЕ ДАННЫЕ:
№ пред-
при-ятия
|
Выпуск кирпича млн. пп:. |
Цена 1-ого кирпича |
Средняя годовая стоимость основных средств, млн.руб |
| Базисный год |
Отчетный год |
Базисный год |
Отчетный год |
Базисный
год
|
Отчетный
год
|
| всего |
в т.ч. экспорт |
всего |
в т.ч. экспорт |
всего |
в т.ч. экспорт |
всего |
в т.ч. экспорт |
| 6 |
35,20 |
7,20 |
36,30 |
7,30 |
10,00 |
13,00 |
11,00 |
13,00 |
18,00 |
18,50 |
| 7 |
29,50 |
6,00 |
30,60 |
6,60 |
8,00 |
11,00 |
9,00 |
12,00 |
18,60 |
18,70 |
| 8 |
29,40 |
6,40 |
29,30 |
6,30 |
9,00 |
12,00 |
9,00 |
12,00 |
18,30 |
18,60 |
| 9 |
40,80 |
8,80 |
45,90 |
9,90 |
10,00 |
12,00 |
11,00 |
13,00 |
21,90 |
23,20 |
| 10 |
39,10 |
8,10 |
40,40 |
8,40 |
10,00 |
13,00 |
12,00 |
15,00 |
19,00 |
19,60 |
| 11 |
38,20 |
7,20 |
40,30 |
8,30 |
9,00 |
12,00 |
10,00 |
13,00 |
20,10 |
22,60 |
| 12 |
34,10 |
6,10 |
34,60 |
6,60 |
8,00 |
11,00 |
9,00 |
12,00 |
18,90 |
19,20 |
| 13 |
27,80 |
7,80 |
28,80 |
5,80 |
9,00 |
12,00 |
9,00 |
12,00 |
18,30 |
18,90 |
| 14 |
34,70 |
5,70 |
35,80 |
7,80 |
8,00 |
11,00 |
9,00 |
13,00 |
19,90 |
21,30 |
| 15 |
27,10 |
4,90 |
27,80 |
5,00 |
9,00 |
12,00 |
10,00 |
13,00 |
18,40 |
18,40 |
| 16 |
32,40 |
7,40 |
36,00 |
6,00 |
10,00 |
13,00 |
12,00 |
14,00 |
19,70 |
21,80 |
| 17 |
29,90 |
6,90 |
29,10 |
6,10 |
9,00 |
11,00 |
10,00 |
12,00 |
16,90 |
17,00 |
| 18 |
30,50 |
5,50 |
30,80 |
6,80 |
9,00 |
12,00 |
10,00 |
14,00 |
18,10 |
19,80 |
| 19 |
38,50 |
8,50 |
38,00 |
8,00 |
10,00 |
12,00 |
11,00 |
15,00 |
19,80 |
19,90 |
| 20 |
34,20 |
6,20 |
36,00 |
7,00 |
9,00 |
11,00 |
11,00 |
14,00 |
17,90 |
18,30 |
| 21 |
34,80 |
6,90 |
35,00 |
7,10 |
10,00 |
12,00 |
11,00 |
13,00 |
18,10 |
18,50 |
| 22 |
39,60 |
10,60 |
39,00 |
9,00 |
9,00 |
12,00 |
10,00 |
13,00 |
20,50 |
22,00 |
| 23 |
31,00 |
5,00 |
30,50 |
6,50 |
8,00 |
11,00 |
9,00 |
12,00 |
17,50 |
17,80 |
| 24 |
34,10 |
6,10 |
34,40 |
6,40 |
9,00 |
12,00 |
9,00 |
13,00 |
19,10 |
21,10 |
| 25 |
35,30 |
7,30 |
36,00 |
7,00 |
9,00 |
12,00 |
10,00 |
14,00 |
18,80 |
19,50 |
| 26 |
29,60 |
6,60 |
30,60 |
5,60 |
8,00 |
11,00 |
9,00 |
12,00 |
17,10 |
17,30 |
| 27 |
33,50 |
7,50 |
34,00 |
5,40 |
9,00 |
12,00 |
10,00 |
13,00 |
18,00 |
18,30 |
| 28 |
35,20 |
5,20 |
35,90 |
8,90 |
9,00 |
11,00 |
10,00 |
14,00 |
18,10 |
18,50 |
| 29 |
39,70 |
8,70 |
41,00 |
9,00 |
9,00 |
12,00 |
10,00 |
13,00 |
20,00 |
21,80 |
| 30 |
30,00 |
6,00 |
30,00 |
6,00 |
9,00 |
11,00 |
10,00 |
14,00 |
17,60 |
17,80 |
| 31 |
40,00 |
8,00 |
39,50 |
8,00 |
10,00 |
13,00 |
12,00 |
15,00 |
19,00 |
19,20 |
| 32 |
29,50 |
5,50 |
30,60 |
6,60 |
9,00 |
12,00 |
10,00 |
14,00 |
18,60 |
19,70 |
| 33 |
28,80 |
7,80 |
29,00 |
6,80 |
8,00 |
11,00 |
9,00 |
13,00 |
18,30 |
18,60 |
| 34 |
40,80 |
6,80 |
41,00 |
8,20 |
9,00 |
12,00 |
10,00 |
14,00 |
21,90 |
22,40 |
| 35 |
39,00 |
7,00 |
40,00 |
7,50 |
9,00 |
11,00 |
11,00 |
13,00 |
19,00 |
19,40 |
| 36 |
38,20 |
6,20 |
39,30 |
7,30 |
10,00 |
12,00 |
12,00 |
14,00 |
20,10 |
22,20 |
| 37 |
34,30 |
5,30 |
34,30 |
6,30 |
9,00 |
11,00 |
10,00 |
12,00 |
18,90 |
19,20 |
| 38 |
27,80 |
5,80 |
28,80 |
6,80 |
8,00 |
12,00 |
9,00 |
13,00 |
18,30 |
18,90 |
| 39 |
34,70 |
6,70 |
34,00 |
6,50 |
9,00 |
12,00 |
11,00 |
13,00 |
20,00 |
21,30 |
| 40 |
27,10 |
5,10 |
27,80 |
5,80 |
8,00 |
11,00 |
9,00 |
12,00 |
18,20 |
18,40 |
| 41 |
32,50 |
7,50 |
36,70 |
7,70 |
9,00 |
11,00 |
10,00 |
13,00 |
19,70 |
21,90 |
| 42 |
29,90 |
5,90 |
29,00 |
6,00 |
10,00 |
13,00 |
12,00 |
15,00 |
16,90 |
17,20 |
| 43 |
30,50 |
5,50 |
30,80 |
6,80 |
9,00 |
12,00 |
10,00 |
14,00 |
18,10 |
19,80 |
| 44 |
38,50 |
6,50 |
38,00 |
7,00 |
8,00 |
11,00 |
9,00 |
13,00 |
19,20 |
19,70 |
| 45 |
34,20 |
5,20 |
36,00 |
6,00 |
9,00 |
12,00 |
10,00 |
14,00 |
17,90 |
18,30 |
1.
Произвести группировку предприятий по стоимости основных производственных фондов в отчетном году
с целью выявления зависимости между размером предприятия по стоимости основных производственных фондов и физическим объемом выработанной продукции.
Результаты представить в виде статистической таблицы, сформулировать выводы.
| Количество групп по формуле Стерджесса |
Размах вариации |
Величина равного интервала |
| 1+3,22*LOG10(40)=6,16 |
23,2-17=6,20 |
6,2/6,16=1,01 |
| Средне-годовая стоимость ОС, млн. руб |
кол-во предпр-иятий |
Расчетные показатели |
| общая средне-годовая стоимость ОС |
средняя стоимость ОС |
общий выпуск кирпича, млн. шт |
средний выпуск |
| до 18 |
5 |
87,10 |
17,42 |
149,20 |
29,84 |
| 18-19 |
13 |
240,90 |
18,53 |
415,30 |
31,94615 |
| 19-20 |
11 |
215,00 |
19,55 |
393,00 |
35,72727 |
| 20-21 |
0 |
0,00 |
0,00 |
| 21-22 |
6 |
129,20 |
21,53 |
217,90 |
36,31667 |
| больше 22 |
5 |
112,40 |
22,48 |
205,50 |
41,1 |
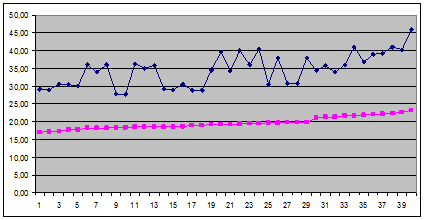
Выводы:
1) Явно прослеживается связь между стоимостью ОС и объемом выпуска: чем больше величина ОС, тем выше объем выпуска.
Это видно, в частности, на графике.
2) Интервал 20-21 пуст, что вообще говоря маловероятно для выборочного метода. Возможна ошибка при сборе статистических сведений.
Это тоже видно на графике: между 29 и 31 ряд резко «подскакивает» вверх.
2.
Построить ряд распределения предприятий по физическому объему выпущенной продукции в отчетном году, рассчитав величину интервала по формуле Стерджесса.
Для построенного ряда определить среднюю арифметическую величину, моду, медиану, показатели вариации, показатель асимметрии.
По правилу 3-х сигм проверить соответствие эмпирического распределения нормальному, сформулировать выводы.
| Количество групп по формуле Стерджесса |
Размах вариации |
Величина равного интервала |
| 6,16 |
18,10 |
2,94 |
4
| выпуск кирпича, млн. шт. |
кол-во предприятий |
Расчетные показатели |
| x'i, середина интервала |
x'i * fi |
кумулята |
| 27,8-30,82 |
15 |
29,31 |
439,65 |
15 |
| 30,82-33,84
|
0
|
32,33
|
15
|
| 33,84-36,86 |
14 |
35,35 |
494,90 |
29 |
| 36,86-39,88 |
5 |
38,37 |
191,85 |
34 |
| 39,88-42,90 |
5 |
41,39 |
206,95 |
39 |
| 42,90-45,92 |
1 |
44,41 |
44,41 |
40 |
| Сумма: |
1377,76 |
Средняя арифметическая интервального ВР: 34,44

Для надежности, вычисляем среднюю арифметическую несгруппированного ряда:

Сумма: 1380,90
Средняя арифметическая ВР:34,52
Здесь можно заметить небольшие различия, в 0,08 (менее одного процента).
Моду вычисляем по формуле:

| мода
|
29,31
|
| модальный интервал:
|
27,8-30,82
|
По накопленным частотам, определяем, что медиана находится в 3м интервале
медиана для несгруппированного ряда: Me=(34,6+35)/2
(20 и 21 элемент ранжированной выборки).
 =33,84+3,02*((40+1/2)-15)/14 = 39,34 =33,84+3,02*((40+1/2)-15)/14 = 39,34
Показатели вариации:
| среднее линейное отклонение
|
дисперсия (взвешенная)
|
| расчетные показатели |
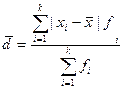 |
расчетные показатели |
| x'i- -x |
|x'i- -x|fi |
x'i- -x |
(x'i- -x)2
|
(x'i- -x) 2
*f i |
| -5,13 |
77,01 |
-5,13 |
26,36 |
395,37 |
| -2,11 |
0,00 |
-2,11 |
4,47 |
0,00 |
| 0,91 |
12,68 |
0,91 |
0,82 |
11,49 |
| 3,93 |
19,63 |
3,93 |
15,41 |
77,07 |
| 6,95 |
34,73 |
 |
6,95 |
48,25 |
241,23 |
| 9,97 |
9,97 |
9,97 |
99,32 |
99,32 |
| 154,02 |
824,48 |
| среднее линейное отклонение
|
3,85
|
дисперсия (взвешенная)
|
20,61
|
среднее квадратическое отклонение = √
D
= √20,61= 4,540
Показатель асимметрии рассчитывается по формуле As = μ3
/σ3
,
но мы воспользуемся более простой формулой: 
(средняя арифметическая минус мода деленное на среднее квадратическое отклонение).
Показатель асимметрии
As
= 1,14,
что значит, что функция плотности скошена влево:
(Если А>0, кривая имеет положительную (правостороннюю) асимметрию).
По правилу 3-х сигм проверить соответствие эмпирического распределения нормальному, сформулировать выводы.
«Правило трех сигм»:
Если случайная величина X имеет нормальный закон распределения с параметрами а
и σ2
, т.е. N[a
; σ2
],
то практически достоверно, что ее значения заключены в интервале (а
- 3σ, а
+ 3σ), где a
- средняя арифметическая.
3σ = 13,487
20,96 ≤ x ≤ 47,93
Действительно, для нашего случая значения не выходят за данные пределы,
а значит, наш ряд распределения может быть распределен по нормальному закону.
3.
Используя ранее выполненную группировку предприятий по стоимости основных фондов, (п.1), проверить правило сложения дисперсий по физическому объему выпущенной продукции.
Правило дисперсии: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии: 
| Средне-годовая стоимость ОС, млн. руб |
кол-во предпр-иятий |
Расчетные показатели
|
| -xi(средний для интервала выпуск продукции) |
x'ifi(общий выпуск кирпича, млн. шт) |
(-xi
- -x0
)(отклонение внутри-групповых средних от общей средней) |
(-xi
- -x0
)2
|
(-xi
- -x0
)2
*ni
|
внутригрупповая дисперсия
σj
2
|
внутригрупповая дисперсия*кол-во элем-в в данной группе
σj
2
*nj
|
| до 18 |
5 |
29,84 |
149,20 |
-4,68 |
21,93 |
109,63 |
0,46 |
2,30 |
| 18-19 |
13 |
31,946 |
415,30 |
-2,58 |
6,64 |
86,29 |
11,74 |
152,62 |
| 19-20 |
11 |
35,727 |
393,00 |
1,20 |
1,45 |
15,97 |
12,99 |
142,89 |
| 20-21 |
0 |
0,00 |
0,00 |
| 21-22 |
6 |
36,317 |
217,90 |
1,79 |
3,22 |
19,31 |
5,25 |
31,50 |
| больше 22 |
5 |
41,1 |
205,50 |
6,58 |
43,26 |
216,32 |
6,27 |
31,35 |
| cумма: |
447,52 |
сумма: |
360,66 |
| общая средняя арифметическая: |
34,52 |
межгрупповая дисперсия: |
11,188 |
средняя из внутригрупповых: |
9,02 |
общая дисперсия:
11,188 + 9,02 = 20,20
| Дисперсия:
|
20,20
|
Внутригрупповая дисперсия
|
| xi - -x |
квадрат |
xi - -xi |
квадрат |
результат: |
| 29,10 |
-5,42 |
29,40 |
29,10 |
-0,74 |
0,55 |
| 29,00 |
-5,52 |
30,50 |
29,00 |
-0,84 |
0,71 |
| 30,60 |
-3,92 |
15,39 |
30,60 |
0,76 |
0,58 |
| 30,50 |
-4,02 |
16,18 |
30,50 |
0,66 |
0,44 |
| 30,00 |
-4,52 |
20,45 |
30,00 |
0,16 |
0,03 |
| 36,00 |
1,48 |
2,18 |
2,29 |
0,46 |
| 34,00 |
-0,52 |
0,27 |
| 36,00 |
1,48 |
2,18 |
36,00 |
4,05 |
16,43 |
| 27,80 |
-6,72 |
45,19 |
34,00 |
2,05 |
4,22 |
| 27,80 |
-6,72 |
45,19 |
36,00 |
4,05 |
16,43 |
| 36,30 |
1,78 |
3,16 |
27,80 |
-4,15 |
17,19 |
| 35,00 |
0,48 |
0,23 |
27,80 |
-4,15 |
17,19 |
| 35,90 |
1,38 |
1,90 |
36,30 |
4,35 |
18,96 |
| 29,30 |
-5,22 |
27,27 |
35,00 |
3,05 |
9,33 |
| 29,00 |
-5,52 |
30,50 |
35,90 |
3,95 |
15,63 |
| 30,60 |
-3,92 |
15,39 |
29,30 |
-2,65 |
7,00 |
| 28,80 |
-5,72 |
32,75 |
29,00 |
-2,95 |
8,68 |
| 28,80 |
-5,72 |
32,75 |
30,60 |
-1,35 |
1,81 |
| 34,60 |
0,08 |
0,01 |
28,80 |
-3,15 |
9,90 |
| 39,50 |
4,98 |
24,78 |
28,80 |
-3,15 |
9,90 |
| 34,30 |
-0,22 |
0,05 |
152,67 |
11,74 |
| 40,00 |
5,48 |
30,00 |
| 36,00 |
1,48 |
2,18 |
34,60 |
-1,13 |
1,27 |
| 40,40 |
5,88 |
34,55 |
39,50 |
3,77 |
14,23 |
| 30,60 |
-3,92 |
15,39 |
34,30 |
-1,43 |
2,04 |
| 38,00 |
3,48 |
12,09 |
40,00 |
4,27 |
18,26 |
| 30,80 |
-3,72 |
13,86 |
36,00 |
0,27 |
0,07 |
| 30,80 |
-3,72 |
13,86 |
40,40 |
4,67 |
21,83 |
| 38,00 |
3,48 |
12,09 |
30,60 |
-5,13 |
26,29 |
| 34,40 |
-0,12 |
0,02 |
38,00 |
2,27 |
5,17 |
| 35,80 |
1,28 |
1,63 |
30,80 |
-4,93 |
24,28 |
| 34,00 |
-0,52 |
0,27 |
30,80 |
-4,93 |
24,28 |
| 36,00 |
1,48 |
2,18 |
38,00 |
2,27 |
5,17 |
| 41,00 |
6,48 |
41,96 |
142,88 |
12,99 |
| 36,70 |
2,18 |
4,74 |
| 39,00 |
4,48 |
20,05 |
34,40 |
-1,92 |
3,67 |
| 39,30 |
4,78 |
22,82 |
35,80 |
-0,52 |
0,27 |
| 41,00 |
6,48 |
41,96 |
34,00 |
-2,32 |
5,37 |
| 40,30 |
5,78 |
33,38 |
36,00 |
-0,32 |
0,10 |
| 45,90 |
11,38 |
129,45 |
41,00 |
4,68 |
21,93 |
| 808,19
|
36,70 |
0,38 |
0,15 |
| 31,49 |
5,25 |
| 39,00 |
-2,10 |
4,41 |
| 39,30 |
-1,80 |
3,24 |
| 41,00 |
-0,10 |
0,01 |
| 40,30 |
-0,80 |
0,64 |
| 45,90 |
4,80 |
23,04 |
| 31,34 |
6,27 |
Вывод. Правило дисперсии выполняется:  , 20,2 = 20,2. , 20,2 = 20,2.
Значит, общая, межгрупповая и средняя внутригрупповых дисперсий рассчитаны верно.
Таким образом, общую дисперсию выпуска продукции (признака) можно разложить на 2 составляющие:
на 11,188 (на 55,4 %) она зависит от объема ОС предприятия,
на 9,02 (на 44,6%) - от прочих факторов.
4. Предприятия, по которым имеются отчетные данные, представляют собой десятипроцентную простую случайную выборку из общего числа предприятий данной отрасли. Требуется определить:
а) среднюю стоимость основных производственных фондов для всех предприятий отрасли в отчетном году, гарантируя результат с вероятностью 0,997;
 |
Отчетный
год
|
Расчетные показатели |
| ОС |
xi
- ¬x |
(xi
- ¬x)2
|
| 17,00 |
-2,61 |
6,84 |
| 17,20 |
-2,42 |
5,83 |
| 17,30 |
-2,31 |
5,36 |
| 17,80 |
-1,81 |
3,29 |
| 17,80 |
-1,81 |
3,29 |
| 18,30 |
-1,31 |
1,73 |
| 18,30 |
-1,31 |
1,73 |
| 18,30 |
-1,31 |
1,73 |
| 18,40 |
-1,22 |
1,48 |
| 18,40 |
-1,22 |
1,48 |
| 18,50 |
-1,11 |
1,24 |
| 18,50 |
-1,11 |
1,24 |
| 18,50 |
-1,11 |
1,24 |
| 18,60 |
-1,01 |
1,03 |
| 18,60 |
-1,01 |
1,03 |
| 18,70 |
-0,91 |
0,84 |
| 18,90 |
-0,71 |
0,51 |
| 18,90 |
-0,71 |
0,51 |
| 19,20 |
-0,41 |
0,17 |
| 19,20 |
-0,41 |
0,17 |
| 19,20 |
-0,41 |
0,17 |
| 19,40 |
-0,21 |
0,05 |
| 19,50 |
-0,11 |
0,01 |
| 19,60 |
-0,01 |
0,00 |
| 19,70 |
0,09 |
0,01 |
| 19,70 |
0,09 |
0,01 |
| 19,80 |
0,19 |
0,03 |
| 19,80 |
0,19 |
0,03 |
| 19,90 |
0,29 |
0,08 |
| 21,10 |
1,49 |
2,21 |
| 21,30 |
1,69 |
2,84 |
| 21,30 |
1,69 |
2,84 |
| 21,80 |
2,19 |
4,77 |
| 21,80 |
2,19 |
4,77 |
| 21,90 |
2,29 |
5,22 |
| 22,00 |
2,39 |
5,69 |
| 22,20 |
2,59 |
6,68 |
| 22,40 |
2,79 |
7,76 |
| 22,60 |
2,99 |
8,91 |
| 23,20 |
3,59 |
12,85 |
| средняя арифметическая:
|
19,62
|
105,69
|
дисперсия: в = σ2
= 105,69/40 = 2,64
СКО = σ = √2,64 = 1,63
Средняя квадратическая ошибка случайной бесповторной выборки
Если бы мы не знали, какой процент от генеральной совокупности составляет выборочная совокупность (40 предприятий), то в таких случаях пришлось бы использовать формулу для
средней квадратической стандартной ошибки простой случайной повторной выборки:
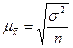
μx
= √σ2
/n = 1,63/ √40 = 1,63/6,32 = 0,258
Но так как мы знаем, какой процент от генеральной совокупности составляет выборочная совокупность (40 предприятий), то в таких случаях приходится использовать формулу для
средней квадратической стандартной ошибки простой случайной повторной выборки:
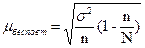
μx
= √σ2
/n(1 - n/N) = 1,63/ √40 ●(1-1/10) = 1,63/6,32●0,9 = 0,258●0,9 = 0,2322
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности ~х
и величину предельной ошибки этой средней Δ¬х
, которая с определенной вероятностью показывает, насколько выборочная средняя может отличаться от генеральной средней в большую или меньшую сторону.
Доверительный интервал для генеральной средней:
~x - tμ¬х
≤ ¬x ≤ ~x + tμ¬х
Величина предельной ошибки выборки равна tμ
t - принятый уровень доверительной вероятности;
μ - величина стандартной ошибки выборки.
При доверительной вероятности 0,997 t = 3
Следовательно, tμ = 3 * 0,232 = 0,70
=> средняя стоимость ОПФ с вероятностью 0,997 находится в интервале
18,92 ≤ 19,62 ≤ 20,32
б) вероятность того, что средняя стоимость основных производственных фондов отличается от полученной по выборке не более, чем на 1,0млн.руб. (на 10% от выборочной средней).
1) случай 1 млн. руб.: 18,62 ≤ 19,62 ≤ 20,62
2) случай 10% (19,62 * 10% = 1,96):
17,66 ≤ 19,62 ≤ 21,58
1 млн = 0,26 * 4 = μ * t
при t = 4 доверительная вероятность равна 1, то есть это достоверно.
Для 2го случая интервал еще шире (в 2 раза).
Следовательно, почти достоверно, что генеральная средняя находится в указанных пределах.
Другими словами, искомая вероятность равна 1.
5. Рассчитав индексы цен Пааше, Ласперса и Фишера. Проанализировать полученные результаты.
№ пред приятия
|
Выпуск кирпича млн. пп:.
|
Цена 1-ого кирпича
|
Расчетные показатели
|
| Базисный год |
Отчетный год |
Базисный год |
Отчетный год |
p0
q0
|
p1
q0
|
p1
q1
|
p0
q1
|
| 6 |
35,20 |
36,30 |
10,00 |
11,00 |
352,00 |
387,20 |
399,30 |
363,00 |
| 7 |
29,50 |
30,60 |
8,00 |
9,00 |
236,00 |
265,50 |
275,40 |
244,80 |
| 8 |
29,40 |
29,30 |
9,00 |
9,00 |
264,60 |
264,60 |
263,70 |
263,70 |
| 9 |
40,80 |
45,90 |
10,00 |
11,00 |
408,00 |
448,80 |
504,90 |
459,00 |
| 10 |
39,10 |
40,40 |
10,00 |
12,00 |
391,00 |
469,20 |
484,80 |
404,00 |
| 11 |
38,20 |
40,30 |
9,00 |
10,00 |
343,80 |
382,00 |
403,00 |
362,70 |
| 12 |
34,10 |
34,60 |
8,00 |
9,00 |
272,80 |
306,90 |
311,40 |
276,80 |
| 13 |
27,80 |
28,80 |
9,00 |
9,00 |
250,20 |
250,20 |
259,20 |
259,20 |
| 14 |
34,70 |
35,80 |
8,00 |
9,00 |
277,60 |
312,30 |
322,20 |
286,40 |
| 15 |
27,10 |
27,80 |
9,00 |
10,00 |
243,90 |
271,00 |
278,00 |
250,20 |
| 16 |
32,40 |
36,00 |
10,00 |
12,00 |
324,00 |
388,80 |
432,00 |
360,00 |
| 17 |
29,90 |
29,10 |
9,00 |
10,00 |
269,10 |
299,00 |
291,00 |
261,90 |
| 18 |
30,50 |
30,80 |
9,00 |
10,00 |
274,50 |
305,00 |
308,00 |
277,20 |
| 19 |
38,50 |
38,00 |
10,00 |
11,00 |
385,00 |
423,50 |
418,00 |
380,00 |
| 20 |
34,20 |
36,00 |
9,00 |
11,00 |
307,80 |
376,20 |
396,00 |
324,00 |
| 21 |
34,80 |
35,00 |
10,00 |
11,00 |
348,00 |
382,80 |
385,00 |
350,00 |
| 22 |
39,60 |
39,00 |
9,00 |
10,00 |
356,40 |
396,00 |
390,00 |
351,00 |
| 23 |
31,00 |
30,50 |
8,00 |
9,00 |
248,00 |
279,00 |
274,50 |
244,00 |
| 24 |
34,10 |
34,40 |
9,00 |
9,00 |
306,90 |
306,90 |
309,60 |
309,60 |
| 25 |
35,30 |
36,00 |
9,00 |
10,00 |
317,70 |
353,00 |
360,00 |
324,00 |
| 26 |
29,60 |
30,60 |
8,00 |
9,00 |
236,80 |
266,40 |
275,40 |
244,80 |
| 27 |
33,50 |
34,00 |
9,00 |
10,00 |
301,50 |
335,00 |
340,00 |
306,00 |
| 28 |
35,20 |
35,90 |
9,00 |
10,00 |
316,80 |
352,00 |
359,00 |
323,10 |
| 29 |
39,70 |
41,00 |
9,00 |
10,00 |
357,30 |
397,00 |
410,00 |
369,00 |
| 30 |
30,00 |
30,00 |
9,00 |
10,00 |
270,00 |
300,00 |
300,00 |
270,00 |
| 31 |
40,00 |
39,50 |
10,00 |
12,00 |
400,00 |
480,00 |
474,00 |
395,00 |
| 32 |
29,50 |
30,60 |
9,00 |
10,00 |
265,50 |
295,00 |
306,00 |
275,40 |
| 33 |
28,80 |
29,00 |
8,00 |
9,00 |
230,40 |
259,20 |
261,00 |
232,00 |
| 34 |
40,80 |
41,00 |
9,00 |
10,00 |
367,20 |
408,00 |
410,00 |
369,00 |
| 35 |
39,00 |
40,00 |
9,00 |
11,00 |
351,00 |
429,00 |
440,00 |
360,00 |
| 36 |
38,20 |
39,30 |
10,00 |
12,00 |
382,00 |
458,40 |
471,60 |
393,00 |
| 37 |
34,30 |
34,30 |
9,00 |
10,00 |
308,70 |
343,00 |
343,00 |
308,70 |
| 38 |
27,80 |
28,80 |
8,00 |
9,00 |
222,40 |
250,20 |
259,20 |
230,40 |
| 39 |
34,70 |
34,00 |
9,00 |
11,00 |
312,30 |
381,70 |
374,00 |
306,00 |
| 40 |
27,10 |
27,80 |
8,00 |
9,00 |
216,80 |
243,90 |
250,20 |
222,40 |
| 41 |
32,50 |
36,70 |
9,00 |
10,00 |
292,50 |
325,00 |
367,00 |
330,30 |
| 42 |
29,90 |
29,00 |
10,00 |
12,00 |
299,00 |
358,80 |
348,00 |
290,00 |
| 43 |
30,50 |
30,80 |
9,00 |
10,00 |
274,50 |
305,00 |
308,00 |
277,20 |
| 44 |
38,50 |
38,00 |
8,00 |
9,00 |
308,00 |
346,50 |
342,00 |
304,00 |
| 45 |
34,20 |
36,00 |
9,00 |
10,00 |
307,80 |
342,00 |
360,00 |
324,00 |
| Индекс Ласперса: |
1,13 |
| Индекс Пааше: |
1,13 |
| Индекс Фишера: |
1,13 |
Индекс Фишера = 1,13
Значит, индекс цен производства кирпичей составил 13%.
6. Определить прирост стоимости произведенной продукции за счет выпуска экспорта в каждом году.
Используем для расчета следующую формулу:
объем выпуска в текущем году * цена в текущем году / объем выпуска в базовом году * цена в базовом году
№ пред-
приятия
|
выпуск кирпича, млн. шт |
цена 1-го кирпича |
Расчетные показатели
|
| базовый год |
отчетный год |
базовый год |
отчетный год |
объем выпуска базов
*цена базовый
|
объем выпуска текущ
* цена текущ
|
| в т.ч. экспорт |
в т.ч. экспорт |
в т.ч. экспорт |
в т.ч. экспорт |
| 6 |
7,20 |
7,30 |
13,00 |
13,00 |
93,60 |
94,90 |
| 7 |
6,00 |
6,60 |
11,00 |
12,00 |
66,00 |
79,20 |
| 8 |
6,40 |
6,30 |
12,00 |
12,00 |
76,80 |
75,60 |
| 9 |
8,80 |
9,90 |
12,00 |
13,00 |
105,60 |
128,70 |
| 10 |
8,10 |
8,40 |
13,00 |
15,00 |
105,30 |
126,00 |
| 11 |
7,20 |
8,30 |
12,00 |
13,00 |
86,40 |
107,90 |
| 12 |
6,10 |
6,60 |
11,00 |
12,00 |
67,10 |
79,20 |
| 13 |
7,80 |
5,80 |
12,00 |
12,00 |
93,60 |
69,60 |
| 14 |
5,70 |
7,80 |
11,00 |
13,00 |
62,70 |
101,40 |
| 15 |
4,90 |
5,00 |
12,00 |
13,00 |
58,80 |
65,00 |
| 16 |
7,40 |
6,00 |
13,00 |
14,00 |
96,20 |
84,00 |
| 17 |
6,90 |
6,10 |
11,00 |
12,00 |
75,90 |
73,20 |
| 18 |
5,50 |
6,80 |
12,00 |
14,00 |
66,00 |
95,20 |
| 19 |
8,50 |
8,00 |
12,00 |
15,00 |
102,00 |
120,00 |
| 20 |
6,20 |
7,00 |
11,00 |
14,00 |
68,20 |
98,00 |
| 21 |
6,90 |
7,10 |
12,00 |
13,00 |
82,80 |
92,30 |
| 22 |
10,60 |
9,00 |
12,00 |
13,00 |
127,20 |
117,00 |
| 23 |
5,00 |
6,50 |
11,00 |
12,00 |
55,00 |
78,00 |
| 24 |
6,10 |
6,40 |
12,00 |
13,00 |
73,20 |
83,20 |
| 25 |
7,30 |
7,00 |
12,00 |
14,00 |
87,60 |
98,00 |
| 26 |
6,60 |
5,60 |
11,00 |
12,00 |
72,60 |
67,20 |
| 27 |
7,50 |
5,40 |
12,00 |
13,00 |
90,00 |
70,20 |
| 28 |
5,20 |
8,90 |
11,00 |
14,00 |
57,20 |
124,60 |
| 29 |
8,70 |
9,00 |
12,00 |
13,00 |
104,40 |
117,00 |
| 30 |
6,00 |
6,00 |
11,00 |
14,00 |
66,00 |
84,00 |
| 31 |
8,00 |
8,00 |
13,00 |
15,00 |
104,00 |
120,00 |
| 32 |
5,50 |
6,60 |
12,00 |
14,00 |
66,00 |
92,40 |
| 33 |
7,80 |
6,80 |
11,00 |
13,00 |
85,80 |
88,40 |
| 34 |
6,80 |
8,20 |
12,00 |
14,00 |
81,60 |
114,80 |
| 35 |
7,00 |
7,50 |
11,00 |
13,00 |
77,00 |
97,50 |
| 36 |
6,20 |
7,30 |
12,00 |
14,00 |
74,40 |
102,20 |
| 37 |
5,30 |
6,30 |
11,00 |
12,00 |
58,30 |
75,60 |
| 38 |
5,80 |
6,80 |
12,00 |
13,00 |
69,60 |
88,40 |
| 39 |
6,70 |
6,50 |
12,00 |
13,00 |
80,40 |
84,50 |
| 40 |
5,10 |
5,80 |
11,00 |
12,00 |
56,10 |
69,60 |
| 41 |
7,50 |
7,70 |
11,00 |
13,00 |
82,50 |
100,10 |
| 42 |
5,90 |
6,00 |
13,00 |
15,00 |
76,70 |
90,00 |
| 43 |
5,50 |
6,80 |
12,00 |
14,00 |
66,00 |
95,20 |
| 44 |
6,50 |
7,00 |
11,00 |
13,00 |
71,50 |
91,00 |
| 45 |
5,20 |
6,00 |
12,00 |
14,00 |
62,40 |
84,00 |
| 3152,50 |
3723,10 |
Прирост стоимости произведенной продукции за счет выпуска экспорта в каждом году.
без учета инфляции (без поправки на индекс Фишера): 1,18
с учетом инфляции 1,18/1,13 = 1,044.
То есть, прирост стоимости составляет 18% либо 4,4%, в зависимости от того, как считать.
|