МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра информатики
Типовой расчет
по дисциплине: «Экономико-математические методы и модели»
по теме: «Сетевое планирование и управление. Основы регрессионного анализа»
Витебск, 2009
 1. Сетевое планирование и управление 1. Сетевое планирование и управление
1.1
Назначение и область применения
Сетевое планирование – это комплекс графических и расчетных методов организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок, например, таких как:
· строительство и реконструкция каких-либо объектов;
· выполнение научно-исследовательских и конструкторских работ;
· подготовка производства к выпуску продукции;
· перевооружение армии.
Характерной особенностью таких проектов является то, что они состоят из ряда отдельных, элементарных работ. Они обусловливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие.
1.2 Сетевая модель и её основные элементы
Основными понятиями сетевых моделей являются понятия события, работы и пути. Построение сетевой модели (структурное планирование) начинается с разбиения проекта на четко определенные работы, для которых определяется продолжительность.
Работа-это некоторый процесс, приводящий к достижению определенного результата, требующий затрат каких-либо ресурсов и имеющий протяженность во времени.
По своей физической природе работы можно рассматривать как:
· действие (заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка);
· процесс (старение отливок, выдерживание вина, травление плат);
· ожидание (ожидание поставки комплектующих, пролеживание детали в очереди к станку).
По количеству затрачиваемого времени работа может быть:
· действительной, т.е. требующей затрат времени;
· фиктивной, т.е. формально не требующей затрат времени и представляющей связь между какими-либо работами (передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению).
Фиктивная работа может реально существовать, например, "передача документов от одного отдела к другому". Если продолжительность такой работы несоизмеримо мала по сравнению с продолжительностью других работ проекта, то формально ее принимают равной 0. Существуют фиктивные работы, которым в реальности не соответствуют никакие действия. Такие фиктивные работы только представляют связь между другими работами сетевой модели. Работы связаны друг с другом таким образом, что выполнение одних работ может быть начато только после
завершения некоторых других.
Событие
– момент времени, когда завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и в отличие от работ не имеет протяженности во времени. Например, фундамент залит бетоном, старение отливок завершено, комплектующие поставлены, отчеты сданы и т.д.
Таким образом, начало и окончание любой работы описываются парой событий, которые называются начальным
и конечным
событиями. Поэтому для идентификации конкретной работы используют код работы (ij), состоящий из номеров начального (i-ro) и конечного (j-ro) событий, например 2-4; 3-8; 9-10.
На этапе структурного планирования взаимосвязь работ и событий изображается с помощью сетевого графика, где работы изображаются стрелками, которые соединяют вершины, изображающие события. Около каждой стрелки ставится среднее время выполнения соответствующей работы. Любое событие может считаться наступившим только тогда, когда закончатся все
входящие в него работы. Поэтому работы, выходящие из некоторого события не могут начаться, пока не будут завершены все операции, входящие в это событие.
работа
i
,
j
Рис. 1.1 –
Кодирование работы
Номер исходного события равен единице. Номера остальных событий соответствуют последней цифре кода предшествующей данному событию работы (или работ).
Событие, не имеющее предшествующих ему событий, т.е. с которого начинается проект, называют исходным
событием. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающим
.
Событие, характеризующее собой факт окончания всех предшествующих работ и начало всех последующих работ, называется промежуточным
или просто событием.
 
Рис. 1.2
Важное значение для анализа сетевых моделей имеет понятие пути.
Путь
– это любая последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Различают следующие виды путей:
Полный
путь
–
это путь от исходного до завершающего события. Критический
путь
– максимальный по продолжительности полный путь. Подкритический путь
– полный путь, ближайший по длительности к критическому пути.
Работы, лежащие на критическом пути, называют критическими.
Каждый путь характеризуется своей продолжительностью (длительностью), которая равна сумме продолжительностей составляющих его работ.
1.3
Правила построения сетевых графиков
При построении сетевого графика необходимо следовать следующим правилам:
· длина стрелки не зависит от времени выполнения работы;
· стрелка не обязательно должна представлять прямолинейный отрезок;
· для действительных работ используются сплошные, а для фиктивных – пунктирные стрелки;
· каждая операция должна быть представлена только одной стрелкой;
· не должно быть параллельных работ между одними и теми же событиями, для избежания такой ситуации используют фиктивные работы;
· следует избегать пересечения стрелок;
· не должно быть стрелок, направленных справа налево;
· номер начального события должен быть меньше номера конечного события;
· не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме исходного;
· не должно быть тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего;
Сетевой график включает в себя работы и события.
Работы на сетевом графике обозначаются стрелками, около которых ставится среднее время выполнения соответствующей работы.
При построении сетевого графика имеют место следующие события:
· исходное событие – это событие, в отношении которого предполагается, что оно не имеет предшествующей работы;
· завершающее событие – это событие, в отношении которого предполагается, что оно не имеет последующих работ;
· промежуточное или просто событие – это событие, характеризующее собой факт окончания всех предшествующих работ и начало всех последующих работ.
Событие обозначается кружком, который содержит следующую информацию:

Номер исходного события равен единице. Номера остальных событий соответствуют последней цифре кода предшествующей данному событию работы (или работ).
При построении сетевого графика должна соблюдаться существующая очерёдность выполнения работ.
Для определения средних значений резервов времени по отдельным событиям определяются средние значения ранних и поздних сроков событий начала и окончания работ.
Путём в сетевом графике называется любая последовательность работ (стрелок), связывающая какие-либо два события. При этом пути, связывающие исходное и завершающее события сети, считаются полными, а все другие пути – неполными. Каждый путь характеризуется своей продолжительностью (длительностью), которая равна сумме продолжительностей составляющих его работ.
Наиболее простым и наглядным методом расчёта параметров сети является графический. Кружки-события заполняются в следующем порядке:
В нижний сектор ставится порядковый номер события.
Путём последовательного перехода от исходного события, ранний срок свершения которого равен нулю, к завершающему событию рассчитываются ранние сроки его свершения. Ранний срок наступления события представляет собой минимальный из возможных моментов наступления должного события при заданной продолжительности работ и начальном моменте.
Ранний срок
наступления j-го события  вычисляется по формуле: вычисляется по формуле:
 ,
i =1,…,к, ,
i =1,…,к,
где  (i =1,…,к) – ранний срок наступления i-го события; (i =1,…,к) – ранний срок наступления i-го события;
 (i =1,…,к) – средняя продолжительность работы ij; (i =1,…,к) – средняя продолжительность работы ij;
к – число работ, непосредственно предшествующих j-му событию.
Ранние сроки определяются величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.
Путём последовательного перехода от завершающего события, поздний срок которого равен величине критического пути, рассчитывают поздний срок
его свершения. Этот срок  определяется разностью продолжительности критического пути и максимальным из путей, следующим за этим событием. определяется разностью продолжительности критического пути и максимальным из путей, следующим за этим событием.
 , j =1,…, , j =1,…, , ,
где 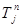 (j=1,…, (j=1,…, ) – поздний срок наступления j-го события; ) – поздний срок наступления j-го события;
 – число работ, непосредственно следующих за i-м событием (все эти работы на сетевом графике обозначаются стрелками, выходящими из кружка, обозначающего i-ое событие). – число работ, непосредственно следующих за i-м событием (все эти работы на сетевом графике обозначаются стрелками, выходящими из кружка, обозначающего i-ое событие).
Поздний срок наступления завершающего события принимается равным раннему сроку наступления того же события.
Разность между поздним и ранним сроками свершения событий – есть резерв времени этого события. Резерв времени i-го события 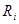 вычисляется по формуле: вычисляется по формуле:
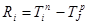 . .
После вычисления резервов времени определяется критический путь 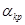 , то есть полный путь, имеющий наибольшую продолжительность. Для него является характерным, что все события, принадлежащие ему, не имеют резервов времени (они равны нулю). , то есть полный путь, имеющий наибольшую продолжительность. Для него является характерным, что все события, принадлежащие ему, не имеют резервов времени (они равны нулю).
Полный резерв времени работы, представляющий собой максимальное время, на которое можно увеличить продолжительность работы (не изменяя длительности критического пути), определяется как разность между поздним сроком свершения события, завершающего работу, и ранним сроком свершения предшествующего работе события минус продолжительность самой работы.
1.4 Решение типовой задачи
На предприятии осуществляется реконструкция цеха. Известна средняя продолжительность выполнения отдельных работ (таблица 1.1). Среднеквадратическое отклонение продолжительности выполнения работ по всем работам равно одному дню.
Необходимо:
1. Построить сетевой график по выполнению работ по реконструкции цеха и определить значение его параметров (ранние и поздние сроки наступления событий, начала и окончания работ, резервы времени по отдельным событиям).
2. Определить на сетевом графике критический путь, дать перечень работ, принадлежащих к критическому пути и его длительность. На сетевом графике выделить критический путь.
Таблица 1.1
| Код работ |
1-2 |
2-3 |
3-8 |
1-4 |
4-6 |
4-7 |
6-7 |
7-8 |
1-5 |
5-8 |
2-4 |
5-6 |
| Продолжительность (дни) |
2 |
4 |
4 |
6 |
5 |
4 |
6 |
5 |
14 |
3 |
1 |
0 |
Определяем ранние сроки наступления j-го события 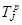 сетевого графика: сетевого графика:

Определяем поздние сроки свершения i- го события  : :
 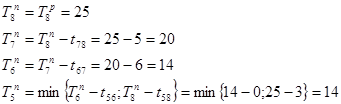

Определим резерв времени i-го события сетевого графика.
Определим критический путь сетевого графика 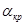 , т.е. полный путь, имеющий наибольшую продолжительность и характеризующийся тем, что все принадлежности ему события не имеют резервов времени (они равны нулю). , т.е. полный путь, имеющий наибольшую продолжительность и характеризующийся тем, что все принадлежности ему события не имеют резервов времени (они равны нулю).
Рассмотрим все пути, проходящие через вершины сетевого графика с нулевыми резервами времени:
1) 1-5-6-7-8
. Его продолжительность равна:
 (дней). (дней).
2) 1-5-8
. Его продолжительность равна:
 (дней). (дней).
Таким образом, критическим путем является путь 1-5-6-7-8 и его продолжительность составляет 25 дней.
Перечень работ, принадлежащих критическому пути, представлен в таблице 1.2.
Таблица 1.2
| Коды работ |
Продолжительность работы (дни) |
| 1-5 |
14 |
| 5-6 |
0 |
| 6-7 |
6 |
| 7-8 |
5 |
Найдём полный резерв времени работ.

Сетевой график выполнения работ по реконструкции цеха представлен на рисунке 1.3.
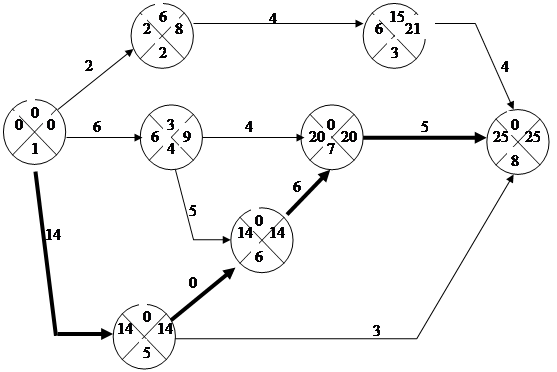
Рисунок 1.3
Ответ:
Таким образом, критический путем является путь 1-5-6-7-8 и его длительность (продолжительность) составляет 25 дней.
2. Основы регрессионного анализа
2.1 Понятие корреляционного и регрессионного анализа
Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, что эти данные являются значениями случайной величины. Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.
При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).
Пример функциональной зависимости выпуск продукции и ее потребление в условиях дефицита.
Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов образование, здоровье и т.д. эта зависимость может быть искажена.
Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом
(от лат.correlatio соотношение, соответствие).
Основная задача корреляционного анализа это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов. Характер связи между показателями определяется по корреляционному полю. Если у
зависимый признак, а х
независимый, то, отметив каждый случай х
(i) с координатами  и и  , получим корреляционное поле. , получим корреляционное поле.
Теснота связи определяется с помощью коэффициента
корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы.
Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от -0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полном ее отсутствии.
Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.
Регрессионный анализсвоей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимо;
i или независимых переменных известна. Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.
По числу факторов различают одно-, двух- и многофакторные уравнения регрессии.
По характеру связи однофакторные уравнения регрессии подразделяются: а) на
линейные:
У=
a
*
bx
,
где х
экзогенная (независимая) переменная, у
эндогенная (зависимая, результативная) переменная, а,
b
параметры;
б) степенные
:
У=
a
*

в) показательные:
У=
a
*

г) прочие.
2.2 Решение типовой задачи
Определить уравнение связи между производительностью труда и рентабельностью предприятия. Вычислить коэффициент корреляции между производительностью труда и рентабельностью предприятия. Проверить гипотезу о значимости отличия коэффициента корреляции от нуля.
Исходные данные представлены в таблице 2.1.
Таблица 2.1
| Уровень рентабельности (млн. руб.) У |
9,3 |
9,2 |
9,5 |
9,6 |
9,1 |
9,0 |
9,2 |
9,5 |
9,8 |
9,0 |
| Производительность труда (тыс. руб.) Х |
138 |
126 |
173 |
188 |
113 |
118 |
121 |
173 |
192 |
118 |
Расчёты произведены с помощью программы KORREL (результаты расчетов представлены в приложении А).
Исходя из наименьшей ошибки аппроксимации, равной 0,7% (приложение А), выбираем гиперболическую зависимость, тогда уравнение связи имеет вид:
 . .
Коэффициент корреляции равен 0,9566. Это говорит о том, что между производительностью труда и рентабельностью предприятия наблюдается сильная положительная корреляционная зависимость.
Задача отыскания уравнения связи состоит в расчёте таких значений коэффициентов  и и  , при которых сумма квадратов отклонений расчётных значений у
от фактических была бы минимальной. , при которых сумма квадратов отклонений расчётных значений у
от фактических была бы минимальной.
В результате расчетов (приложение А) получены следующие значения коэффициентов:  =-177,0966, =-177,0966,  =10,5833. =10,5833.
Таким образом, уравнение связи между производительностью труда и рентабельностью предприятия имеет вид:
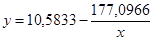 . .
Используя MS
EXCEL, находим расчетные значения у
(таблица 2.2).
Таблица 2.2
| X |
Yфактич
|
Yрасч
|
| 138 |
9,3 |
9,3000 |
| 126 |
9,2 |
9,1778 |
| 173 |
9,5 |
9,5596 |
| 188 |
9,6 |
9,6413 |
| 113 |
9,1 |
9,0161 |
| 118 |
9,0 |
9,0825 |
| 121 |
9,2 |
9,1197 |
| 173 |
9,5 |
9,5596 |
| 192 |
9,8 |
9,6609 |
| 118 |
9,0 |
9,0825 |
По данным таблицы 2.2 строим графики с использованием MSEXCEL (рисунок 2.1).

Рисунок 2.1
Ответ:
Таким образом, произведенный анализ показывает, что величина рентабельности предприятия очень сильно связана с производительностью труда (коэффициент корреляции равен 0,9566) гиперболической зависимостью. Уравнение регрессии имеет вид:
 , где , где
х
– производительность труда, тыс. руб.;
у – рентабельность предприятия, млн. руб.
Приложение
Линейная функция
Х среднее: 146.00000
Х^2 среднее:22224.40000
Y среднее: 9.32000
Сумма Х:1460.00000
Сумма У: 93.20000
Сумма ХУ:13681.50000
Сумма Х^2:222244.00000
Сумма Х^3:35206964.00000
Сумма Х^4:5779526020.00000
Сумма Х^5:977620238660.00000
Сумма Х^6:169393426206244.00000
Сигма Х: 3.01396748489429E+0001
Сигма Y: 2.56124969498246E-0001
Линейная зависмость...
Коэфф. линейной корреляции: 9.62494665792165E-0001
Коэффициент регрессии: 8.17921620434764E-0003
Критерий z Фишера: 1.97874428159125E+0000
B линейн: 8.12583443416641E+0000
M линейн: 8.17921620434764E-0003
Коэффициент элластичности: 1.27293114526625E+0002
Ошибка аппроксимации:100.00%
Квадратическая функция
Х среднее: 146.00000
Х^2 среднее:22224.40000
Y среднее: 9.32000
Сумма Х:1460.00000
Сумма У: 93.20000
Сумма ХУ:13681.50000
Сумма Х^2:222244.00000
Сумма Х^3:35206964.00000
Сумма Х^4:5779526020.00000
Сумма Х^5:977620238660.00000
Сумма Х^6:169393426206244.00000
Сигма Х: 3.01396748489429E+0001
Сигма Y: 2.56124969498246E-0001
Квадратическая зависмость...
B1: 3.46922673040546E-0003
B2: 1.55057167225825E-0005
B0: 8.37472964616692E+0000
Коэфф. тесноты связи: 8.89956472480589E-0001
Критерий t Стьюдента: 1.21031231930916E+0001
Ошибка аппроксимации: 1.01%
Гиперболическая функция
Х среднее: 146.00000
Х^2 среднее:22224.40000
Y среднее: 9.32000
Сумма Х:1460.00000
Сумма У: 93.20000
Сумма ХУ:13681.50000
Сумма Х^2:222244.00000
Сумма Х^3:35206964.00000
Сумма Х^4:5779526020.00000
Сумма Х^5:977620238660.00000
Сумма Х^6:169393426206244.00000
Сигма Х: 3.01396748489429E+0001
Сигма Y: 2.56124969498246E-0001
Гиперболическая зависмость...
B0: 1.05833048281678E+0001
B1:-1.77096572793607E+0002
Коэфф. тесноты связи: 9.56563625865627E-0001
Критерий t Стьюдента: 3.18354736234179E+0001
Ошибка аппроксимации: 0.70%
Степенная функция
Х среднее: 146.00000
Х^2 среднее:22224.40000
Y среднее: 9.32000
Сумма Х:1460.00000
Сумма У: 93.20000
Сумма ХУ:13681.50000
Сумма Х^2:222244.00000
Сумма Х^3:35206964.00000
Сумма Х^4:5779526020.00000
Сумма Х^5:977620238660.00000
Сумма Х^6:169393426206244.00000
Сигма Х: 3.01396748489429E+0001
Сигма Y: 2.56124969498246E-0001
Степенная зависмость...
b0: 9.32981521162895E+0000
b1:-7.19246032216071E-0005
Коэфф. тесноты связи: 9.56563625865627E-0001
Критерий t Стьюдента: 3.18354736234179E+0001
Ошибка аппроксимации: 2.41%
Показательная функция
Х среднее: 146.00000
Х^2 среднее:22224.40000
Y среднее: 9.32000
Сумма Х:1460.00000
Сумма У: 93.20000
Сумма ХУ:13681.50000
Сумма Х^2:222244.00000
Сумма Х^3:35206964.00000
Сумма Х^4:5779526020.00000
Сумма Х^5:977620238660.00000
Сумма Х^6:169393426206244.00000
Сигма Х: 3.01396748489429E+0001
Сигма Y: 2.56124969498246E-0001
Показательная зависимость...
A: 9.26805458600855E+0000
B: 1.00003571231918E+0000
Коэфф. тесноты связи: 2.71410458071453E-0001
Критерий t Стьюдента: 8.28710533241120E-0001
Ошибка аппроксимации: 2.29%
Таблица
Z
r 0 1 2 3 4 5 6 7 8 9
0.0 0.0000 0.0100 0.0200 0.0300 0.0400 0.0500 0.0601 0.0701 0.0802 0.0902
0.1 0.1003 0.1104 0.1206 0.1307 0.1409 0.1511 0.1614 0.1717 0.1820 0.1923
0.2 0.2027 0.2132 0.2237 0.2342 0.2448 0.2554 0.2661 0.2769 0.2877 0.2986
0.3 0.3095 0.3205 0.3316 0.3428 0.3541 0.3654 0.3769 0.3884 0.4001 0.4118
0.4 0.4236 0.4356 0.4477 0.4599 0.4722 0.4847 0.4973 0.5101 0.5230 0.5361
0.5 0.5493 0.5627 0.5763 0.5901 0.6042 0.6184 0.6328 0.6475 0.6625 0.6777
0.6 0.6931 0.7089 0.7250 0.7414 0.7582 0.7753 0.7928 0.8107 0.8291 0.8480
0.7 0.8673 0.8872 0.9076 0.9287 0.9505 0.9730 0.9962 1.0203 1.0454 1.0714
0.8 1.0986 1.1270 1.1568 1.1881 1.2212 1.2562 1.2933 1.3331 1.3758 1.4219
0.9 1.4722 1.5275 1.5890 1.6584 1.7380 1.8318 1.9459 2.0923 2.2976 2.6466
0.99 2.6466 2.6996 2.7587 2.8257 2.9031 2.9945 3.1063 3.2504 3.4534 3.8002
Таблица
t
Число степеней свободы P=0.95 P=0.99 Число степеней свободы P=0.95 P=0.99
1 12.69 63.655 2 4.302 9.924
3 3.183 5.841 4 2.777 4.604
5 2.571 4.032 6 2.447 3.707
7 2.364 3.500 8 2.307 3.356
9 2.263 3.250 10 2.227 3.169
11 2.200 3.138 12 2.179 3.055
13 2.161 3.012 14 2.145 2.977
15 2.131 2.946 16 2.119 2.921
17 2.110 2.898 18 2.100 2.877
19 2.093 2.860 20 2.086 2.846
21 2.078 2.832 22 2.074 2.818
23 2.069 2.807 24 2.064 2.795
25 2.059 2.787 26 2.054 2.778
27 2.052 2.771 28 2.049 2.764
29 2.045 2.757 30 2.042 2.750
32 2.037 2.739 34 2.032 2.728
36 2.027 2.718 38 2.025 2.711
40 2.020 2.704 42 2.017 2.696
44 2.015 2.691 46 2.012 2.685
48 2.010 2.681 50 2.007 2.678
55 2.005 2.668 60 2.000 2.661
65 1.997 2.653 70 1.994 2.648
|