1. МОДЕЛІ ПОВЕДІНКИ СПОЖИВАЧІВ
В теорії споживання вважається, що споживач керується принципом рацiональностi: вiн завжди прагне максимізувати свою корисність, i єдине, що його стримує, — це обмежений дохід:
max u(x)
(1.1)
px = M
де х=(х1
,...,хn
)′
– вектор-стовпчик обсягів споживчих товарів, що придбав споживач за заданих цін; n
– число різноманітних товарів; u(х)
– функція корисності споживача; р = (p1
,…,pn
) – вектор-рядок цін товарів; М
– обсяг доходу споживача.
Це задача на умовний екстремум, i її розв’язок зводиться до знаходження безумовного екстремуму функції Лагранжа:
L(x,λ)=u(x)-λ(px-M)
.
Необхідними умовами локального екстремуму є:
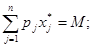 (1.2) (1.2)
  (1.3) (1.3)
Точка екстремуму справді визначає точку максимуму, оскільки матриця Гессе U(х)=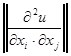 є вiд’ємно визначеною. З виразу (1.3) бачимо, що споживач за фіксованого доходу так обирає набір
є вiд’ємно визначеною. З виразу (1.3) бачимо, що споживач за фіксованого доходу так обирає набір  , що в цій точці відношення граничної корисності дорівнює відношенню цін: , що в цій точці відношення граничної корисності дорівнює відношенню цін:
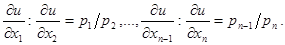
Якщо розв’язати (1.2), (1.3) відносно  , отримаємо функцію попиту споживача: , отримаємо функцію попиту споживача:
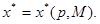
2. РІВНЯННЯ СЛУЦЬКОГО
Розглянемо, як зміниться попит споживача, що визначається моделлю (1.1), якщо зміниться ціна одного з товарів. Нехай ціна n
-го товару зросла на 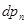 . Це приводить до такої зміни попиту на товари . Це приводить до такої зміни попиту на товари
 (2.1) (2.1)
де р
– вектор-рядок цін; U
– матриця Гессе;  – вектор-стовпчик попиту на товари; – вектор-стовпчик попиту на товари; 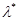 – множник Лагранжа; – множник Лагранжа;  – індекс n
за дужками біля матриці означає, що взято й n
-й стовпчик. – індекс n
за дужками біля матриці означає, що взято й n
-й стовпчик.
Проаналізуємо зміст складових, що входять у рівняння (2.1).
Зміна попиту за збільшення ціни з компенсацією доходу. Нехай дохід споживача збільшився на таку величину 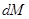 , яка компенсує споживачеві збільшення ціни на n
-й товар (благо) на , яка компенсує споживачеві збільшення ціни на n
-й товар (благо) на 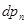 . .
Збільшення ціни з компенсацією доходу приводить до такої зміни попиту:
 (2.2) (2.2)
Тобто друга складова у правій частині рівняння (2.1) — це зміна попиту, якщо зростання ціни n
-го товару на 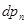 компенсується збільшенням доходу на компенсується збільшенням доходу на 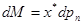 . .
Зміна попиту за зміни доходу. Якщо дохід змінюється на 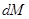 , то відповідно змінюється попит: , то відповідно змінюється попит:
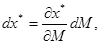
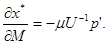 (2.3) (2.3)
Об’єднуючи вирази (2.1), (2.2), (2.3), отримаємо рівняння Слуцького, яке є серцевиною теорії корисності:
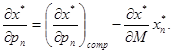 (2.4) (2.4)
Оскільки вивчається зміна попиту за зростання ціни на n
-й товар, що не компенсується підвищенням доходу, то друга складова в (2.4) (з від’ємним знаком) знімає штучний приріст по спричинений компенсуючим зростанням доходу.
Ефект доходу полягає у змiнi споживання внаслідок зміни реального доходу, яка виникла через зміну цін.
Ефект заміщення полягає у змiнi споживання внаслідок зміни відносних цін.
Графік представлено на малюнку 2.1

Малюнок 2.1 - Графік
3. МОДЕЛІ ПОВЕДІНКИ ВИРОБНИКІВ
Моделі оптимального (раціонального) вибору виробника (фірми). Нехай виробнича фірма випускає один продукт (чи багато продуктів, але з постійною структурою). Позначимо річний випуск у натурально-речовiй формі через Х
– кількість одиницьпродукту одного виду, вектор-стовпчик можливих обсягів різних видів ресурсів через х
=
(х1
,
...,
хn
)′
. Тоді технологія фірми визначатиметься її виробничою функцією, яка виражає зв'язок між випуском i витратами ресурсів:
Х=F(х).
Припускається, що F(х)
двiчi неперервно диференційована, неокласична, i матриця її других похідних є вiд’ємно визначеною.
Якщо  –вектор-рядок цін ресурсів, а р
– цінапродукції, то кожному вектору витрат х
вiдповiдає прибуток: –вектор-рядок цін ресурсів, а р
– цінапродукції, то кожному вектору витрат х
вiдповiдає прибуток:
 (3.1) (3.1)
У (3.1)  –вартість річного випуску фірми,або її річний дохід, –вартість річного випуску фірми,або її річний дохід, 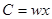 – витрати виробництва чи вартість витрат ресурсів за рік. – витрати виробництва чи вартість витрат ресурсів за рік.
Якщо не вводити інших обмежень, крім невід’ємних обсягів витрат ресурсів, то задача знаходження максимуму прибутку набере вигляду:
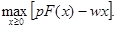  (3.2) (3.2)
Це задача нелiнiйного програмування з n
умовами невід’ємності: 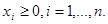 Необхідними умовами існування екстремуму є умови Куна-Таккера: Необхідними умовами існування екстремуму є умови Куна-Таккера:
 (3.3) (3.3)
Якщо в оптимальному розв’язку використовуються всi види ресурсів, тобто 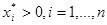 , то умови (3.3) матимуть вигляд: , то умови (3.3) матимуть вигляд:
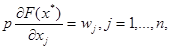 (3.4) (3.4)
тобто в оптимальній точці вартість граничного продукту даного ресурсу повинна дорівнювати його цiнi.
Розглянемо задачу знаходження максимуму випуску за заданого обсягу витрат
 (3.5) (3.5)
Це задача нелiнiйного програмування з одним лiнiйним обмеженням i умовою невiд’ємностi змінних. Побудуємо функцію Лагранжа

і знайдемо її максимум за умови невiд’ємностi змiнних. Для цього необхідно, щоб виконувались умови Куна-Таккера:
 (3.6) (3.6)
Як бачимо, якщо покласти  , умови (3.6) збiгаються з умовами (3.3). , умови (3.6) збiгаються з умовами (3.3).
|