1.Понятие о стат таблице. Элементы стат таблицы.
Таблица
– это рациональное изображение цифрового материала, полученного в результате статистического наблюдения. Таблица состоит из 1) макета, 2) цифрового материала. Макет: заголовочная часть, отделяется жирными линиями, остаточная часть – хвост, котор в свою очередь делится на боковик (первую слева графу) и прографку (остальные части таблицы).
Заголовочная часть включает в себя заголовок и подзаголовок. Справа наверху пишется номер таблицы, чуть ниже посередине – её название. Название должно содержать объект, место и время действия. Каждая таблица состоит из 2х элементов – подлежащего и сказуемого. Подлежащее
– это то, о чём говорится в данной таблице (объект исследования). Подлежащее записывается слева в таблице по строкам. Сказуемое
– это то, что говорится о подлежащем. Сказуемое записывается справа в графах. В зависимости от построения подлежащего и сказуемого различают простые и сложные таблицы. Простая
– подлежащее которой не огруппировано. Это таблица подлежащее которой содержит перечень единиц наблюдения (перечневая таблица), хронологических дат (хронолог таблица) или территориальных подразделений (территориальная таблица) Такие табл имеют чисто описательный хар-р. Их задача показать существенные типы соц-эк явлений.
Групповая
- это табл подлежащее котор содержит группировку единиц наблюдения по одному существенному признаку.
Комбинационная
- это табл подлежащее котор содержит группировку ед-ц наблюдения по двум или нескольким существенным признакам взятым в совкупности.
2. Понятие о статистическом графике. Элементы статистического графика.
График – это наглядное изображение табличного материала. Любой график строится на основании таблицы. График состоит из: графический образ, поле графика, пространственные и масштабные ориентиры, экспликация графика. Полем графика является место, на котором он выполняется. Графический образ — это символические знаки, с помощью которых изображаются статистические данные (линии, точки, прямоугольники, квадраты, круги и т.д.). Пространственные ориентиры определяют размещение графических образов. Масштабные ориентиры придают этим образам колич определенность. Вводятся ось абсцисс и ось ординат, как правило, используется равномерная линейная шкала и на осях откладываются масштабы. Экспликация графика — это пояснение его содержания, включает в себя заголовок графика, объяснения масштабных шкал, условные обозначения. Графики различают в соответствии с 2 признаками: 1) графич образ, 2) задачи, решаемые с помощью графика. 1)Графич образы выбираются в зависим от цели, поставленной перед графиком. В завис от гр образа различают виды графиков: точечные, линейные, полосовые, столбиковые, квадратные, круговые, секторные, прямоугольные, фигурные. Графики важны не только для придания наглядности, но и имеют большое аналитическое значение. Посредством графиков выявляются качественные особенности и тенденции в развитии явлений, изучается структура и динамика сложных совокупностей, устанавливается теснота связей между признаками, обнаруживаются ошибки в статистических материалах.
3. Формы и виды статистического наблюдения.
Статистическое наблюдение
– это первая стадия всякого статистического исследования, представляющая собой научно организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни, и сбор полученных на основе этого учета массовых данных. Статистическое наблюдение должно быть планомерным, массовым и систематическим. К статистическому наблюдению предъявляются следующие требования:1) полноты и практической ценности статистических данных; 2) достоверности и точности данных; 3) их единообразия и сопоставимости. По форме: 1)отчётность, 2)специально организованное.
Отчетность
- форма наблюдения при которой стат. орг-ции в опред. срок получают от организаций и пр-ий необходимые стат. данные в виде отчетов по установленным формам. Спец. орг-ное
пров-ся с целью получения сведений, отсутств-щих в отчётности, или для проверки её данных ( пример-перепись).
Перепись – получение необходимых данных путем спец обследований.
С точки зрения полноты охвата фактов статистическое наблюдение может быть сплошным и несплошным. Сплошное
наблюдение представляет собой полный учет всех единиц изучаемой совокупности.
Несплошное
наблюдение организуют как учет части единиц совокупности, на основе которой можно получить обобщающую характеристику всей совокупности. К видам несплошного наблюдения относятся: способ основного массива, выборочные наблюдения, монографические описания. Выборочное – по принципу случайного отбора, обследованию подвергается часть единиц совокупности, отобранная на основании научных принципов, обеспечивающих получение достаточно достоверных данных для хар-ки всей совокупности. Монографическое – подробное описание одной или нескольких ед совокупности.(высокая детализация) , для выявления имеющ-ся или намеч-ся тенденций в развитии данного явл-я. Основного массива- подверг-ся самые крупные единицы изуч-ой совок-ти, имеют наиб-ый удельный вес в общей сов-ти (работа городских рынков).
По времени регистрации: Текущие
- фиксир-ся по мере их наступления (рождение, смерть, брак) Периодически
е- перепись населения каждые 10 лет. Единовременное
- сведения о коллич-ых хар-ах явления или процесса в момент его исследования (повторная регистр-ия спустя какое-то время).
По способу стат-го набл-ия: непосредственное, документальное, опрос: анкетный, корреспондентский, экспедиционный. Документальное – на основе учетных документов. Непосредственное – обследование совокупности в натуре (обмер, взвешивание). Опросное – регистрация данных со слов опрошенных.
 4. Виды группировок. Их определение и область применения на предприятиях нг профиля. 4. Виды группировок. Их определение и область применения на предприятиях нг профиля.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная).
Типологическая
группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей). Структурная
дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. Аналитическая (факторная)
группировка позволяет оценивать связи между взаимодействующими признаками. В зависимости от числа положенных в их основание признаков различают простые и сложные группировки. Группировка, выполненная по одному признаку, называется простой. Сложн группировка производится по двум и более признакам. Частным случаем сложн группировки явл комбинационная группировка, базирующаяся на 2-4 признаках, взятых во взаимосвязи, многомерная – свыше 6 признаков.Типологическая
- явл. группир-ки, построенные по соц.-экономич-им или классовым признакам с целью выделения их хар-ки соц.-эк. типов. Структурные
- явл. группировки, постр-ые по ряду характ их признаков с целью выявл-ия стр-ры и структ-ых изм-й в совок-ти однотипных ед-ц. Аналитические
- явл. гр-ки, харак-ие взаимосвязь между изучаемыми понятиями. Среди простых группировок особо выделяют ряды распределения. Ряд распределения – это группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель – численность группы. Сущ. первичная и вторичная гр-ки: Вторичная группировка
– образованная по данным первичной. Цель вторичной группировки
: образование на осн группировок по количественным признакам качественно однородных групп, приведение группировок с различными интервалами к единому виду в целях сравнимости, обр-ие более укрупнённых групп в кот-ых яснее проступает хар-р распред-я
5. Статистическая сводка, её задачи и этапы проведения.
Научно организованная обработка материалов наблюдения (по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой.
Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности. Программа сводки включает определение групп и подгрупп; системы показателей; видов таблиц. Этапы проведения сводки:
Выбор группируемого признака, Определение порядка формирования группы, Разработка системы статистический показателей, Разработка макета стат. таблицы. 5. Статистическая сводка, её задачи и этапы проведения.
Научно организованная обработка материалов наблюдения (по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой.
Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности. Программа сводки включает определение групп и подгрупп; системы показателей; видов таблиц. Этапы проведения сводки:
Выбор группируемого признака, Определение порядка формирования группы, Разработка системы статистический показателей, Разработка макета стат. таблицы. По форме обработки материала сводка бывает централизованной и децентрализованной. При децентрализованной сводке, кот., как правило, используется при обработке стат. отчетности, разработка материала производится последовательными этапами. Так, отчеты предприятий сводятся стат. органами субъектов РФ, а уже итоги по региону поступают в Госкомстат России, и там определяются показатели в целом по народному хозяйству страны.
При централизованной сводке весь первичный материал поступает в одну организацию, где и подвергается обработке от начала до конца.
Централизованная сводка обычно используется для обработки материалов единовременных стат. исследований.
По технике выполнения стат. сводка м. б. механизированной и ручной.
6. Принципы построения статистической группировки и классификации.
Группировка
– это разбиение совокупности на группы, однородные по какому-либо признаку (объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам) Устойчивое разграничение объектов выражается классификацией
, которая основывается на самых существенных признаках (например, классификация отраслей народного хозяйства, классификация основных фондов и т.д.). Таким образом, классификация – это узаконенная, общепринятая, нормативная группировка.
Метод группировки основывается на следующих категориях – это группировочный признак, интервал группировки и число групп.
Группировочный признак
– это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Интервал
очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Интервалы бывают:
равные
, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова; неравные
, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе; открытые
, когда имеется только либо верхняя, либо нижняя граница; закрытые
, когда имеются и нижняя, и верхняя границы.
Определение числа групп.
Здесь необходимо учитывать несколько условий: а) число групп детерминируется уровнем колеблемости группировочного признака. Чем значительнее вариация признака, тем больше при прочих равных условиях должно быть групп; б) число групп должно отражать реальную структуру изучаемой совокупности;
в) не допускается выделение пустых групп. Если проблема пустых групп все же возникает, при проведении структурных группировок используют неравные интервалы. Для нахождения числа групп служит формула
 где N – количество элементов совокупности. где N – количество элементов совокупности.
В случае равных интервалов величина интервала может быть определена как
 или или 
7. Задачи и основные типа группировок.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная).
Типологическая
группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей). Структурная
дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. Аналитическая (факторная)
группировка позволяет оценивать связи между взаимодействующими признаками. В зависимости от числа положенных в их основание признаков различают простые и сложные группировки. Группировка, выполненная по одному признаку, называется простой. Сложн группировка производится по двум и более признакам. Частным случаем сложн группировки явл комбинационная группировка, базирующаяся на 2-4 признаках, взятых во взаимосвязи, многомерная – свыше 6 признаков. Среди простых группировок особо выделяют ряды распределения. Ряд распределения – это группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель – численность группы. Сущ. первичная и вторичная гр-ки: Вторичная группировка
– образованная по данным первичной. Цель вторичной группировки
: образование на осн группировок по количественным признакам качественно однородных групп, приведение группировок с различными интервалами к единому виду в целях сравнимости, обр-ие более укрупнённых групп в кот-ых яснее проступает хар-р распред-я
8. Ряды распределения и группировки.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная).
Типологическая
группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей). Структурная
дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. Аналитическая (факторная)
группировка позволяет оценивать связи между взаимодействующими признаками. В зависимости от числа положенных в их основание признаков различают простые и сложные группировки. Группировка, выполненная по одному признаку, называется простой. Сложн группировка производится по двум и более признакам. Частным случаем сложн группировки явл комбинационная группировка, базирующаяся на 2-4 признаках, взятых во взаимосвязи, многомерная – свыше 6 признаков. Среди простых группировок особо выделяют ряды распределения. .
Рядом распр-я
наз. ряд цифровых показат-ей, представл-их распределение единиц сов-ти по одному сущ-му приз-ку, разновидности кот-го расположены в опред последоват.
Вариационные ряды распределения состоят их двух элементов вариантов и частот.
Вариантами
называются числовые значения колличественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными. Частоты
– это численности отдельных вариантов или каждой группы вариационного ряда. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.
Ряды распр-я могут быть образованы по качественному(атрибутивному) и колич-му пр-ку. В первом случае они наз. атрибутивными ,а во втором- вариационными.
Вариационные ряды распр-ия по сп-бу постр-ия бывают дискретные и интервальные:
Дискр. вариац. ряд распр-я
- группы сост-ны по признаку, изменяющемуся дискретно и приним-му только целые значения. Интервальный вариац. ряд распр-ия
- группировачный признак, сост-ий групп-ки, может принимать в опред-ом интервале любые знач-ия. Число ед-ц частоты, приходящиеся на ед-цу инт-ла наз. плотностью распред-я
. Ряд накопл-ых частот (кумулятивный)-показ-т число случаев ниже или выше опред-го уровня. Графич изображения ряда распред.: линейные, плоскостные диаграммы, гистограммы, куммулятивная кривая (изображ-ет ряд накопл-х частот)
9. Средняя арифметическая взвешенная.
При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид: X средн = (EXi*fi)/ Efi
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.
Расчет средней по способу моментов.
Основан на свойствах средней арифметической. В качестве условного ноля – X0 выбирают середину одного из центральных интервалов, обладающего наибольшей частотой.Этот способ используется только в рядах с равными интервалами.
10. Средняя гармоническая простая и взвеш.
 Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая
используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1: Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая
используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
 К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость: К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость:

В статист практике чаще исп гармонич взвеш
, формула кот имеет вид:
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.
Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров. Допустим, необходимо узнать среднюю цену реализованных товаров: Вид товара Цена за единицу, руб.Сумма реализаций, руб.
а 50 500
б 40 600
с 60 1200
 Получаем Получаем
 Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна: Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна:
11. Упрощенный расчет средней арифм. (ср. ар.) (способ моментов).
Пользуясь св-ми ср. ар., ее можно рассчитать след. образом: 1) вычесть из всех вариант постоянное число (лучше значение серединной варианты); 2) разделить варианты на постоянное число – на величину интервала; 3) частоты выразить в %. Вычисление ср. ар. первыми двумя способами называется способом отсчета от условного начала (способом моментов). Этот способ применяется в рядах с разными интервалами. Ср. ар. в этом случае опред. по ф-ле:
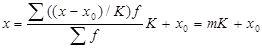  Где m – момент первого порядка; х0
– начало отсчета; К – величина интервала. Где m – момент первого порядка; х0
– начало отсчета; К – величина интервала.
12. Мода и медиана.
 Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Медиана
(Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда. Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина. Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10) : 2= 8,5. То есть для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле Nme=(n+1)/2, где n - число единиц в совокупности. Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. Численное значение медианы обычно определяют по формуле----- где xМе - нижняя граница медианного интервала; i - величина интервала; S-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала. Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Медиана
(Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда. Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина. Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10) : 2= 8,5. То есть для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле Nme=(n+1)/2, где n - число единиц в совокупности. Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. Численное значение медианы обычно определяют по формуле----- где xМе - нижняя граница медианного интервала; i - величина интервала; S-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала.
Модой (Мо)
называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой. Чтобы найти конкретное значение моды, необходимо использовать формулу

где xМо - нижняя граница модального интервала; iМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным.
Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики.
13. Свойства средней ариф. (ср. ар.)
1.Если из всех вариантов ряда (-) или ко всем вариантам (+) постоянное число, то ср. ар. соответственно уменьшится или увеличится на это число. 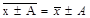 .2.Если все варианты ряда умножить или разделить на постоянное число, то ср. ар. соответственно увеличится или уменьшится в это число раз. .2.Если все варианты ряда умножить или разделить на постоянное число, то ср. ар. соответственно увеличится или уменьшится в это число раз.  3.Если все частоты увеличить или уменьшить в постоянное число раз, то средняя от этого не изменится. 3.Если все частоты увеличить или уменьшить в постоянное число раз, то средняя от этого не изменится. 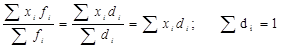 . .
4.Сумма отклонений всех вариантов ряда от ср. ар. = 0. (Нулевое свойство средней). 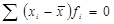 . 5. . 5. Σfi
=Σfixi
. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты. Σfi
=Σfixi
. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты.
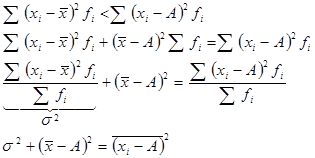 6.Сумма квадратов отклонений всех вариантов ряда от ср. ар. < суммы квадратов их отклонений от любого другого постоянного числа. Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии + квадрат разности между средней и числом А. 6.Сумма квадратов отклонений всех вариантов ряда от ср. ар. < суммы квадратов их отклонений от любого другого постоянного числа. Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии + квадрат разности между средней и числом А.
Данное св-во положено в основу метода наименьших квадратов, кот. широко применяется в исследовании стат. взаимосвязей.
14. Виды дисперсий. Правило их сложения
.
 Различают три вида дисперсий: общая; средняя внутригрупповая; межгрупповая. Общая дисперсия (2
о
)
характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле 2
о
= (X – Xо средн)2
*f / f, где Xо средн - общая средняя арифметическая всей исследуемой совокупности. Средняя внутригрупп дисперс
(2
средн
) свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам (2
i
), затем рассчитывается средняя внутригрупповая дисперсия (2
i
cредн): где ni - число единиц в группе. Межгрупповая дисперсия Различают три вида дисперсий: общая; средняя внутригрупповая; межгрупповая. Общая дисперсия (2
о
)
характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле 2
о
= (X – Xо средн)2
*f / f, где Xо средн - общая средняя арифметическая всей исследуемой совокупности. Средняя внутригрупп дисперс
(2
средн
) свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам (2
i
), затем рассчитывается средняя внутригрупповая дисперсия (2
i
cредн): где ni - число единиц в группе. Межгрупповая дисперсия
 характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле
 где - средняя величина по отдельной группе. Все три вида дисперсии связаны между собой: общая дисперсия равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии: где - средняя величина по отдельной группе. Все три вида дисперсии связаны между собой: общая дисперсия равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии:
 Данное соотношение отражает закон, который называют правилом сложения дисперсий. Согласно этому закону (правилу), общая дисперсия, которая возникает под влиянием всех факторов, равна сумме дисперсий, которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки. Данное соотношение отражает закон, который называют правилом сложения дисперсий. Согласно этому закону (правилу), общая дисперсия, которая возникает под влиянием всех факторов, равна сумме дисперсий, которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки.
15
. Виды средних. Их исчисление
.

16. Показатели вариации, применяемые в статистике.
Вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления. Для измерения вариации в статистике применяют несколько способов. Наиболее простым явл расчет показателя размаха вариации
Н как разницы между Xmax и Xmin: H=Xmax - Xmin. Но размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается. Среднее линейное отклонение
d - среднее арифметическое значение абсолютных отклонений признака от его среднего уровня: в = (Xi – X средн) / n. При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной. В статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии:
δ = (Xi – X средн)2
/n. Показатель s, равный √δ2
, называется средним квадратическим отклонением.
Величина Mx = √(δ2
/n)-средняя ошибка выборки и явля хар-кой отклонения выборочного среднего значения призн от его истинной средней величины. Показатель средней ошибки использ при оценке достоверности результатов выборочн наблюд. Коэфф осцилляции
отражает относит колеблемость крайних значений признака вокруг средней: Ko = (R/X средн)*100%. Относительное линейное отключение
характеризует долю усредненного значения признака абсолютных отклонений от средней величины Kd = (d средн/ X средн)*100%. Коэффициент вариации:
V = (δ/X средн)*100%
17. Простейшие приёмы обработки рядов динамики.
Простейшими видами обработки рядов динамики являются: укрупнение интервалов, метод скользящей средней, аналитическое выравнивание, экстраполяция и интерполяция.
Укрупнение интервалов.
Ряд динамики разделяют на достаточно большое число равных интервалов. Если средн уровни по интервалам не позволяют увидеть тенденцию разв, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (уменьшая количество интервалов). Скользящая средняя.
В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Для того чтобы создать модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание
ряда динамики. Простейшими моделями, выражающими тенденцию развития, являются: линейная функция прямой, показательная функция, парабола, парабола n-порядка, гипербола, экспонента. Иногда возникает необходимость предвидеть будущий уровень ряда динамики. В таких случаях прибегают к приему обработки рядов динамики, называемому экстраполяцией
: yn
+1
= yn
+ ∆yn
+∆∆yn
,
гдеyn
+1
- неизвестный уровень ряда, yn
- последний известный уровень ряда, ∆yn
- цепной абсолютный прирост последнего уровня ряда (∆yn
= yn
- yn
-1
), ∆∆yn
- изменение прироста последнего уровня ряда. Наряду с экстраполяцией иногда применяется такой прием обработки рядов динамики, как интерполяция
- искусственное нахождение отсутствующих членов внутри динамического ряда. Неизвестный уровень ряда находится по формуле: yi
= (yi
+1
+ yi
-1
) / 2. Где: yi
- неизвестный уровень ряда, yi
+1
- последующий за неизвестным уровень ряда, yi
-1
- предыдущий уровень ряда.
18. Виды рядов динамики, их хар-ка и возможности сложения значений ряда.
Изменение общественного процесса или явления во времени называется динамикой. А ряды последовательно расположенных в хронологическом порядке показателей, характеризующих динамику (развитие) общественного явления, образуют ряды динамики
. Ряды динамики характеризуются двумя показателями: показатель времени t
(годы, кварталы, месяцы) и уровень ряда y
. Показатели уровней рядов динамики могут быть выражены абсолютными, относительными и средними величинами. Путем обработки рядов динамики абсолютных показателей получают ряды динамики относительных и средних величин. Статистические показатели могут характеризовать либо результаты изучаемого процесса за период времени, либо состояние изучаемого явления на определенный момент времени, т.е. показатели могут быть интервальными (периодическими) и моментными. Моментные ряды динамики в свою очередь могут быть с равными и неравными промежутками времени. Первоначальные ряды динамики могут быть преобразованы в ряд средних величин и ряд относительных величин (цепной и базисный). Такие ряды динамики называют производными рядами динамики. Моментный
- ряд динамики, уровни которого характеризуют состояние явления на определенные моменты времени. Например, на определенные моменты времени характеризуется динамика стоимости основных фондов, протяженности трубопроводов и т.д. В моментных рядах динамики период между датами, на которые приводятся данные, называется интервалом ряда. Величина интервала зависит от характера явлений. Так, для явлений, быстро развивающихся, ряды динамики должны иметь более короткий интервал. В каждом последующем уровне содержится полностью или частично предыдущий уровень. Поэтому суммировать уровни моментного ряда не следует
во избежание повторного счета. Важное экономическое значение имеет определение разности уровней моментного ряда динамики, которая характеризует развитие (увеличение или уменьшение) изучаемого явления во времени. Интервальный
– ряд динамики, уровни которого характеризуют размер общественного явления или процесса за определенный период времени (год, месяц, пятилетку и т.д.). В интервальном ряду динамики отражаются результаты функционирования производительных сил общества, деятельности людей, а также затраты, связанные с их деятельностью. Так, объем добытой за год нефти определяют путем ежедневного его подсчете. Также учитывают и затраты материалов, труда и других элементов на добычу нефти. Величина интервала – это накопленный итог учета результатов деятельности, то есть величина уровней интервального ряда зависит от размаха интервала. Уровни интервального ряда в отличие от уровней моментного ряда не содержатся в предыдущих или последующих показателях. Поэтому важное экономическое значение имеет суммирование этих уровней
. Сумма уровней интервального ряда динамики характеризует уровень данного явления за более длительный отрезок времени.
19. Сглаживание рядов динамики скользящей средней
.
Ряд динамики – ряд числовых показателей, характеризующий изм размеров общественных явлений и процессов во времени.
Обработка рядов динамики преследует цель выявить тенденцию динамики. Иногда для этого бывает достаточно укрупнить интервалы (в интервальных рядах). Но чаще приходится прибегать к более сложным приемам: сглаживанию рядов с помощью скользящей средней или к аналитическому выравниванию рядов.
Сглаживание рядов динамики скользящей средней. Расчет скользящей средней
: определяются укрупненные периоды, подсчитывается среднее значение нескольких укрупненных членов ряда (3-5), начиная с 1, затем со 2, и т д. Таким образом, средняя как бы скользит по ряду динамики, передвигаясь на один срок. В рез-те такого выравнивания сглаживаются незначительные случайные колебания и более отчетливо проявляется общее направление в развитии явления.
20. Средние показатели рядов динамики
Система средних показателей динамики включает: средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
- Средний уровень интервального ряда: Ycp = Yi / n, n-число значений
- Средний уровень моментного ряда (определяется по средней хронологической): Ycp = (0,5Yo + Y1 + Y2 + … + 0,5Yn) / n-1, 0.5Yo - ср. знач. за 2 периода
- Абсол средн прирост:Ycp = (Yi – Yi-1)/n-1цепной.Ycp=(Yn–Yo) / n-1базисный
- Средний темп роста: tcp = корень (n-1)-ой степени из Yn/Yo.
Yn- n-ый период, Yo- базисный
tcp = корень (n-1)ой степени из t1*t2*…*tnцепной
- Средний темп прироста: tcp = tcp – 100(если темп роста в процентах)
21. Показатели анализа рядов динамики.
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.

26. Цепные и базисные индексы.
В ходе экономического анализа изменение индексируемых величин часть изучают не за два, за ряд последовательных периодов. Возникает необходимость построения индексов за ряд этих последовательных периодов.
В зависимости от выбора базы сравнения индексы бывают цепными и базисными. В системе базисных индексов
сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а системе цепных индексов
уровни индексируемого показателя сопоставляются с уровнем предыдущего периода. Цепные и базисные индексы могут быть как индивидуальные
, так и общие
. Индивидуальные базисные индексы:
ip
=
pn
\
po
.
Индивидуальные цепные индексы:ip
=
pn
\
pn
-1.
Между цепными и базисными индивидуальными индексами существует взаимосвязь - произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода
: Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода
:
27. Метод цепных подстановок. Область применения.
В ряде случаев требуется сравнить данные не за два, а за три и более периодов. В таких случаях необходимо выбрать базу сравнения. В зависимости от базы сравнения различают индексы базисные и цепные. Под базисными индексами понимают такие индексы, которые имеют один и тот же период времени, взятый за основу расчетов. Если же при расчете индекса база для расчетов будет меняться и в качестве такой базы берут период, предшествующий вычислению индекса, тогда этот индекс получит название цепного. И цепные и базисные индексы могут быть с переменными или постоянными весами. Индексы с переменными весами вычисляются по весам индексируемых периодов. Индексы с постоянными весами вычисляются по весам одного какого-то периода. Берем три года 1977-79.
1.Отделим базисные индексы физического объема продукции с постоянными весами:
I 1979/1977
= Σq2p0 / Σq0p0. I 1978/1977
= Σq1p0 / Σ q0p0.
2.Определим цепные индексы физического объема продукции с постоянными весами:
I 1979/1978
= Σq2p0 / Σq1p0. I 1978/1977
= Σq1p0 / Σq0p0.
3.Определим цепные индексы цен с переменными весами.
I 1978/1977
= Σq1p1 / Σq1p0. I 1979/1978
= Σq2p2 / Σq3p1.
Базисные и цепные индексы взаимосвязаны:
-Произведение цепных индексов дает базисный индекс последнего периода. I 1979/1977
=I1978/1977
* I1979/1978
. Эта связь характерна только для индексов с постоянными весами. -Отношение последующего базисного индекса к предшествующему равно цепному индексу последующего периода. I1979/1977
/ I1978/1977
= I1979/1978
. Область применения
:
Для анализа динамики производительности труда может применяться разновидность индексного метода - метод цепных подстановок. Этот метод используют для факторного анализа производительности труда. Сущность его состоит в том, что производительность труда выражают в виде произведения факторов, влияющих на нее, и находят влияние каждого фактора на изменение производительности труда.
28. Понятия промышленной продукции.
Промышленная продукция - это материальные ценности, создаваемые трудом в сфере промышленно-производственной деятельности.
К продукции промышленного предприятия относится только результат его промышленно-производственной и хозяйственной деятельности, материальные ценности, приобретенные со стороны как-то: сырье, топливо и т.п. - к которым не был приложен труд работников данного предприятия, но которые могут быть им реализованы, не являются продукцией этого предприятия. Различают готовую продукцию, полуфабрикаты и незавершенное производство.
К готовой продукции
относятся такие изделия, производство которых на данном промышленном предприятии полностью закончено. Эти изделия должны соответствовать установленным для них стандартам или утвержденным техническим условиям и быть укомплектованными необходимыми частями, инструментами и т.п. Моментом готовности изделия считается приемка изделия отделом технического контроля (ОТК), который проверяет соответствие качества продукта требованиям ГОСТа (государственного стандарта). После сдачи изделия на склад, предприятие учитывает данную продукцию как готовую к передаче заказчикам.
Полуфабрикатами
являются такие продукты, которые в пределах данного предприятия должны подвергаться дальнейшей обработке. Но если полуфабрикаты отпускаются на сторону, т.е. реализуются другим предприятиям, то такое изделие относится к категории готовой продукции. Примером полуфабрикатов может служить чугун, выработанный на металлургическом комбинате, когда этот чугун должен подвергнуться обработке для получения стали, а сталь является тоже полуфабрикатом, поскольку она должна быть предварительным материалом для получения проката. Но если чугун или сталь реализуются другими предприятиями, то такой продукт является готовым изделием или продукцией данного предприятия.
Незавершенное производство
представляет собой также продукты, которые еще не закончены в соответствии с требованиями технологического процесса. Чугун или сталь предназначенные для производства проката на данном металлургическом комбинате является "незавершенкой" в рамках данного предприятия. брак не продукция, даже если реализован. Производств.услуги – это рез-т деят-ти. Кот.сводится не к созданию новых мат.ценностей, а к воостановлению утраченной потребит.стоимости, созданной на другом предприятии.К ним относятся: кап.ремонт, текущий ремонт, модерн.оборудования, транспортных ср-в, мех-змов, приборов. Как правило, работы пром.хар-ра учитываются в стоимостном выражении.
29. Стоимостные показатели промышленной продукции.
Стоимостные (ценностные) показатели являются более приемлемыми в качестве обобщающих показателей величины, объема произведенной продукции на данном предприятии или отрасли в целом, а также и по всему народному хозяйству.
Умножая количество произведенных продуктов на их цены и суммируя полученные произведения, получают обобщающий показатель количества произведенной продукции в ценностном выражении. С помощью данного показателя учитываются также объемы произведенных полуфабрикатов, незавершенного производства и другие виды выполненной работы промышленными предприятиями. Оценка в стоимостных показателях работы промышленных предприятий предполагает фиксирование результатов деятельности производственных структур на определенную дату или в рамках определенного отрезка времени.
При выборе оценочного показателя в стоимостном выражении необходимо также пользоваться одними и теми же разновидностями цен, и именно, ценами оптовыми, розничными, ценами предприятий или ценами промышленности данной отрасли. Однако и в этом смысле цены должны характеризоваться одними и теми же принципами их формирования.
30. Учет продукции в натуральном, условно-натуральном и стоимостном выражении.
Пром. прод-ия учитывается в натуральном, стоимостном и условно-натуральном выражении. Итоговые показатели объема продукции, полностью отражающие результаты произв-ной деят-ти в целом, можно получить с помощью стоимостного метода
.
Стоимость одного вида прод-ии рассчитывается как произведение цены единицы прод-ии на ее объем: S = P*Q
При определении стоимости продукции на предприятии применяются отпускные цены предприятия. Различают цены действующие и неизменные. В действующих ценах рассчитывают товарную и реализованную продукцию, а в неизменных- выражают валовую. Иногда валовая, товарная и реализованная прод-ия оценивается в одних оптово-отпускных ценах.
Учет прод-ии в натуральном выражении
ведется по отчетной, т.е. заранее установленной номенклатуре продуктов. В натур. выражении учет ведется по предприятию и его структурным подразделениям (цехам, установкам, участкам и т.д.) Учитывается про-во готовых изделий и полуфабрикатов по видам, сортам, размерам, артикулам и т.д. Единицы измерения продукции в натуральном выражении, то есть в физических мерах: штуки; тонны; метры и т.д. В ряде случаев выпуск определенных видов продукции выражается не в одной, а в двух единицах измерения. Стальные трубы, например, учитываются в тоннах и метрах, электромоторы в штуках и киловаттах мощности.
В дополнение и развитие учета продукции в натуральном выражении в ряде случаев осуществляется учет ее в условных натуральных
единицах. Сущность метода условных единиц состоит в том, что количество всех продуктов выражается в количестве какого-либо одного вида, единицу которого принимают за условную. Пересчет производится путем перемножения количеств каждого вида продукции на соответствующие коэф-ты перевода в условные единицы. Основное значение приобретает при этом принцип, положенный в основу построения переводных коэффициентов. Коэф. перевода должны быть построены исходя из соотношений продуктов по основному потребительскому свойству. В этом случае выражение прод. в усл. ед-цах дает большее представление о ее объеме как определенной массе потребительных ст-тей, чем выражение прод. в натур. ед-цах. Метод пересчета натур. ед-ц прод. в условные не рекомендуется использовать при выпуске разнородной и разноименной прод. Разновидностью метода условных ед-ц является метод трудочасов или нормочасов. В основе его заложена трудоемкость продуктов, то есть весь объем произведенной прод. выражается в нормах трудовых затрат. В производствах нефтяной пром-сти находят применение все три метода учета прод.
|
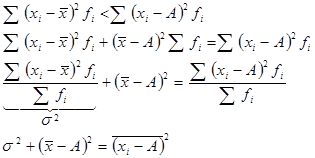 6.Сумма квадратов отклонений всех вариантов ряда от ср. ар. < суммы квадратов их отклонений от любого другого постоянного числа. Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии + квадрат разности между средней и числом А.
6.Сумма квадратов отклонений всех вариантов ряда от ср. ар. < суммы квадратов их отклонений от любого другого постоянного числа. Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии + квадрат разности между средней и числом А.
