| Министерство науки и образования Украины
Днепропетровский Национальный Университет
Радиофизический факультет
Кафедра физики СВЧ
Реферат по курсу
электродинамики:
“Система уравнений Максвелла в сплошной среде.
Граничные условия”
Выполнил:
Студент
группы РЭ–01-1 А. Л. Бузмаков
Проверил:
Доцент
Кафедры оптоэлектроники
Физического ф-та: В. Д. Гладуш
Днепропетровск 2003
Содержание
- Уравнения Максвелла в дифференциальной и интегральной форме.
- Граничные условия.
- Уравнения Максвелла в системе уравнений магнитостатики и электростатики.
- Пример.
- Приложение.
- Формула Остроградского-Гаусса.
- Формула Стокса.
- Список используемой литературы.
1. Уравнения Максвелла в дифференциальной и интегральной форме
Система уравнений, состоящая из уравнений Максвелла для электромагнитного поля и уравнений Ньютона для частиц, представляет собой единую систему уравнений, описывающую все явления, обусловленные электромагнитным взаимодействием (без учёта релятивистских и квантовых эффектов). Поэтому, строго говоря, их необходимо решать совместно в задачах электродинамики. Однако в такой наиболее общей постановке решать задачи о взаимодействии электромагнитного поля с веществом чрезвычайно трудно. Сложность проблемы заключается в том, что вещество состоит из громадного количества частиц, движение которых каждой в отдельности невозможно описать. С такой проблемой сталкиваются в классической механике при попытках описать механическое движение газов, жидкостей и твёрдых тел. Чтобы обойти эту трудность физикам приходилось строить определённые модели механических систем: модель абсолютно твёрдого тела, модель сплошной среды и др. При изучении взаимодействия заряженных частиц с электромагнитным полем также приходится вводить некоторые модели. Одной из таких широко употребляемых, является модель сплошной среды, состоящая из электрических диполей (диэлектрик
). Эта модель электрического диполя играет очень важную роль в физике, так как атомы и молекулы представляют собой системы заряженных частиц, которые в целом нейтральны, но могут обладать отличным от нуля дипольным моментом и поэтому создавать электрическое поле.
Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впоследствии. Основным следствием теории Максвелла был вывод о существовании электромагнитных волн, распространяющихся со скоростью света.
Основу теории образуют уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике. Ниже приведена полная система уравнений Максвелла классической электродинамики в сплошной среде.
Первую пару уравнений Максвелла образуют уравнения:
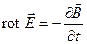 (1) (1)
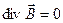 (2) (2)
Здесь вектор 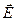 - вектор напряжённости электрического поля, - вектор напряжённости электрического поля, 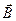 - вектор индукции магнитного поля. - вектор индукции магнитного поля.
Первое из этих уравнений связывает значение 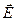 с изменениями вектора с изменениями вектора 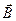 во времени и является по существу выражением закона электромагнитной индукции. Оно показывает, что источником вихревого поля вектора во времени и является по существу выражением закона электромагнитной индукции. Оно показывает, что источником вихревого поля вектора 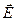 является меняющееся со временем вихревое магнитное поле. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов, как в вакууме, так и в намагниченном веществе. является меняющееся со временем вихревое магнитное поле. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов, как в вакууме, так и в намагниченном веществе.
Вторую пару уравнений Максвелла образуют уравнения:
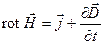 (3) (3)
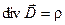 (4) (4)
Где 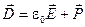 - вектор электрического смещения, - вектор электрического смещения, 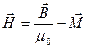 - напряжённость магнитного поля, - напряжённость магнитного поля, 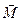 - намагниченность вещества, - намагниченность вещества, 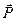 - поляризованность, - поляризованность, 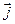 - вектор плотности тока, - вектор плотности тока, 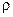 - объёмная плотность заряда. - объёмная плотность заряда.
Первое уравнение устанавливает связь между токами проводимости и токами смещения, и порождаемым ими магнитным полем. Второе показывает, что источниками вектора 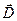 служат сторонние заряды. служат сторонние заряды.
Вышеперечисленные уравнения представляют собой дифференциальную форму уравнений Максвелла. Можно отметить, что в первую пару уравнений входят только основные характеристики поля - 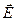 и и 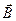 . Во второй паре фигурируют только вспомогательные величины . Во второй паре фигурируют только вспомогательные величины 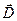 и и  . .
Можно отметить, что вид уравнений (2) и (4) не зависит от наличия среды, в то время как векторы 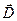 и и  , а также величины , а также величины 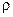 и и 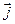 , входящие в уравнения (3) и (4), зависят от свойств вещества и условий, в которых оно находится. Любое макроскопическое тело, рассматриваемое как сплошная среда, состоит из заряженных частиц – электронов и ядер, обладающих также и магнитными моментами, и поэтому взаимодействующих с электромагнитным полем, являясь в то же время и его источниками. Таким образом, величины , входящие в уравнения (3) и (4), зависят от свойств вещества и условий, в которых оно находится. Любое макроскопическое тело, рассматриваемое как сплошная среда, состоит из заряженных частиц – электронов и ядер, обладающих также и магнитными моментами, и поэтому взаимодействующих с электромагнитным полем, являясь в то же время и его источниками. Таким образом, величины 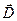 , ,  , , 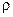 и и 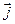 следует определять, исходя из электрических и магнитных свойств вещества. следует определять, исходя из электрических и магнитных свойств вещества.
Выводя формулу (1), Максвелл предположил, что изменяющегося со временем магнитное поле обусловливает появление в пространстве поля  , независимо от присутствия в пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля. , независимо от присутствия в пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
Рассмотрим случай электромагнитной индукции, когда проволочный контур, в котором индуцируется ток, неподвижен, а изменения магнитного потока обусловлены изменениями магнитного поля. Возникновение индукционного тока свидетельствует о том, что изменения магнитного поля вызывают появление в контуре сторонних сил, действующих на носители тока. Эти сторонние силы не связаны ни с химическими, ни с тепловыми процессами в проводе; они также не могут быть магнитными силами, потому что такие силы над зарядами работы не совершают. Остаётся заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем. Обозначим напряжённость этого поля  (это обозначение является вспомогательным так же как и (это обозначение является вспомогательным так же как и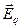 ). Электродвижущая сила равна циркуляции вектора ). Электродвижущая сила равна циркуляции вектора  по данному контуру: по данному контуру:
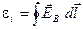 (1.1) (1.1)
Подстановка в формулу 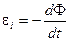 выражения (1.1) для выражения (1.1) для 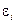 и выражения и выражения 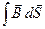 для для 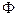 приводит к соотношению приводит к соотношению
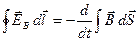
(интеграл в правой части берётся по произвольной поверхности, опирающейся на контур). Поскольку контур и поверхность неподвижны, операции дифференцирования по времени и по поверхности можно поменять местами:
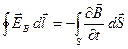 (1.2) (1.2)
В связи с тем, что вектор 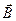 зависит, вообще говоря, как от времени, так и от координат, то можно написать под знаком интеграла символ частной производной по времени (интеграл зависит, вообще говоря, как от времени, так и от координат, то можно написать под знаком интеграла символ частной производной по времени (интеграл 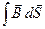 является функцией только времени). является функцией только времени).
Левую часть равенства (1.2) преобразуем по теореме Стокса. В результате получится:
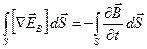 . .
Ввиду произвольности выбора поверхности интегрирования должно выполняться равенство
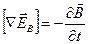 . .
Ротор поля 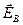 в каждой точке пространства равен взятой с обратным знаком производной по времени от вектора в каждой точке пространства равен взятой с обратным знаком производной по времени от вектора 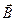 . .
Это поле 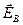 , порождающееся изменением магнитного поля, существенно отличается от порождаемого электрическими зарядами электрического поля , порождающееся изменением магнитного поля, существенно отличается от порождаемого электрическими зарядами электрического поля  . Электростатическое поле потенциально, его линии начинаются и заканчиваются на зарядах. Ротор вектора . Электростатическое поле потенциально, его линии начинаются и заканчиваются на зарядах. Ротор вектора  в любой в любой
точке равен нулю:
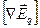 =0. =0.
Согласно (1.2) ротор вектора 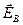 отличен от нуля. Следовательно, поле отличен от нуля. Следовательно, поле 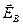 так же, как и магнитное является вихревым. Линии напряжённости так же, как и магнитное является вихревым. Линии напряжённости 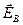 замкнуты. замкнуты.
Таким образом, электрическое поле может быть как потенциальным ( ) так и вихревым ( ) так и вихревым (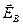 ). В общем случае электрическое поле слагается из этих двух полей. Сложив вместе ). В общем случае электрическое поле слагается из этих двух полей. Сложив вместе  и и 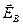 , получим следующее уравнение: , получим следующее уравнение:
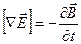 . (1.3) . (1.3)
Существование взаимосвязи между электрическим и магнитным полями служит причиной того, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электростатическое поле создаётся системой неподвижных зарядов в одной системе координат, однако они могут двигаться относительно другой инерциальной системы отсчёта и тогда они будут во второй системе подвижными, следовательно, будут создавать магнитное поле. Таким образом, поле, которое относительно некоторой системы отсчёта оказывается «чисто» электрическим или «чисто» магнитным, относительно других систем отсчёта будет представлять собой совокупность электрического и магнитных полей, образующих единое электромагнитное поле.
Выводя формулу (3), Максвелл пересмотрел уравнения для ротора вектора  для случая стационарного (не изменяющегося со временем) электромагнитного поля, где ротор вектора для случая стационарного (не изменяющегося со временем) электромагнитного поля, где ротор вектора  равен в каждой точке плотности тока проводимости: равен в каждой точке плотности тока проводимости:
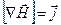 , (3.1) , (3.1)
где вектор 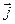 связан с плотностью заряда в той же точке уравнением непрерывности: связан с плотностью заряда в той же точке уравнением непрерывности:
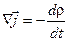 (3.2) (3.2)
Электромагнитное поле может быть стационарным лишь при условии, что плотность заряда 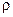 и плотность тока и плотность тока  не зависят от времени. В этом случае согласно (3.2) дивергенция не зависят от времени. В этом случае согласно (3.2) дивергенция  равна нулю. равна нулю.
Поэтому можно выяснить, является ли справедливым уравнение (3.2) справедливым в случае изменяющихся со временем полей. Рассмотрим магнитное поле, создаваемое током, текущим при зарядке конденсатора от источника постоянного напряжения U
(рис. 1).
  Этот ток непостоянен во времени (в момент, когда напряжение на конденсаторе становится равным U
, ток прекращается). Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора. Этот ток непостоянен во времени (в момент, когда напряжение на конденсаторе становится равным U
, ток прекращается). Линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора.
Возьмём круговой контур Г, охватывающий провод, по которому течёт ток к конденсатору, и проинтегрируем соотношение (3.1) по пересекающеё провод поверхности S
1
, ограниченной контуром:
 . .
Преобразовав левую часть по теореме Стокса, получим циркуляцию вектора 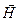 по контуру Г: по контуру Г:
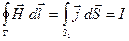 (3.3) (3.3)
(I
– сила тока заряжающего конденсатор). Проделав такие же вычисления для поверхности S
2
, придём к явно неверному соотношению:
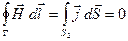 (3.4) (3.4)
Полученный результат указывает на то, что в случае изменяющихся со временем полей уравнение (3.1) перестаёт быть справедливым. Напрашивается вывод, что в этом уравнении отсутствует слагаемое, зависящее от произвольных полей во времени. Для стационарных полей это слагаемое обращается в нуль.
На неправомерность уравнения (3.1) в случае нестационарных полей указывает также, следующие соображения. Возьмём дивергенцию от обеих частей соотношения (3.1):
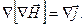
Дивергенция ротора должна быть обязательно равна нулю. Таки образом, можно прийти к выводу, что дивергенция вектора 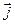 также должна быть всегда равной нулю. Однако этот вывод также должна быть всегда равной нулю. Однако этот вывод
противоречит уравнению непрерывности, где 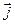 отлична от нуля. отлична от нуля.
Чтобы согласовать уравнения (3.1) и (3.2), Максвелл ввел в правую часть уравнения (3.1) дополнительное слагаемое. Естественно, что это слагаемое должно иметь размерность плотности тока. Максвелл назвал его плотностью тока смещения
. Таким образом, согласно Максвеллу уравнение (3.1) должно иметь вид:
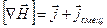 (3.5) (3.5)
Сумму тока проводимости и тока смещения принято называть полным током. Плотность полного тока равна:
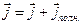 (3.6) (3.6)
Если положить дивергенцию тока смещения равной дивергенции тока проводимости, взятой с обратным знаком,
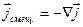 (3.7) (3.7)
то дивергенция правой части уравнения (3.5), так же как и дивергенция левой части, всегда будет равна нулю.
Заменив в (3.7) 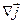 согласно (3.2) через согласно (3.2) через 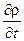 , получим следующее выражение для дивергенции тока смещения: , получим следующее выражение для дивергенции тока смещения:
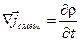 . (3.8) . (3.8)
Чтобы связать ток смещения с величинами, характеризующими изменение электрического поля со временем, воспользуемся соотношением:
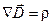
Продифференцировав это соотношение по времени, получим:

Теперь поменяем в левой части порядок дифференцирования по времени и по координа -там. В результате придём к следующему выражения для производной  по по  . .
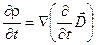 . .
Подстановка этого выражения в формулу (3.8) даёт:
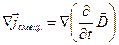 . .
Отсюда
 (3.9) (3.9)
Подставив выражение (3.9) в формулу (3.6), придём к уравнению
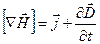 . .
Каждое из векторных уравнений (1) и (3) эквивалентно трем скалярным уравнениям, связывающим компоненты векторов, стоящих в левой и правой частях равенств. Воспользовавшись правилом раскрытия дифференциальных операторов, можно записать их в следующем виде:
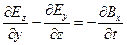 ; ; 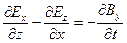 ; ;  (5) (5)
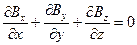 (6) (6)
для первой пары уравнений, и:
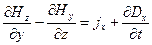 ; ; 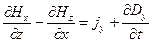 ; ; 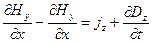 (7) (7)
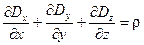 (8) (8)
для второй.
Всего получилось 8 уравнений, в которых входят 12 функций (по три компоненты векторов 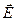 , , 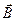 , , 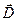 , , 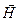 .) Поскольку число уравнений меньше числа известных функций, уравнений (1) - (4) недостаточно для нахождения полей по заданным распределениям зарядов и токов. Чтобы осуществить расчёт полей, нужно дополнить уравнения Максвелла уравнениями, связывающими .) Поскольку число уравнений меньше числа известных функций, уравнений (1) - (4) недостаточно для нахождения полей по заданным распределениям зарядов и токов. Чтобы осуществить расчёт полей, нужно дополнить уравнения Максвелла уравнениями, связывающими 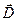 и и 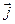 с с 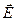 , а также , а также 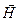 с с 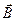 . Эти уравнения имеют вид. . Эти уравнения имеют вид.
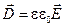 (9) (9)
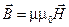 (10) (10)
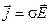 (11) (11)
Совокупность уравнений (1) – (11) образуют основу электродинамики покоящихся сред.
Уравнения:
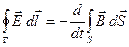 (12) (12)
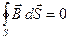 (13) (13)
(первая пара) и
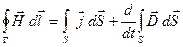 (14) (14)
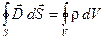 (15) (15)
(вторая пара) представляют собой уравнения Максвелла в интегральной форме.
Уравнение (12) получается путём интегрирования соотношения (1) по произвольной поверхности S
с последующим преобразованием левой части по теореме Стокса в интеграл по контуру Г
, ограничивающему поверхность S
. Уравнение (14) получается таким же способом из соотношения (3). Уравнения (13) и (15) получаются из соотношений (2) и (4) путём интегрирования по произвольному объёму V
с последующим преобразованием левой части по теореме Остроградского-Гаусса в интеграл по замкнутой поверхности S
, ограничивающей объём V
.
2. Граничные условия
При решении задач электродинамики, учитывается, что все макроскопические тела ограничены поверхностями. При переходе через эти поверхности физические свойства макроскопических тел изменяются скачком и поэтому также скачком могут изменяться электромагнитные поля, создаваемые этими телами. Другими словами векторные функции 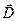 и и 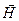 являются кусочно-непрерывными функциями координат, т.е. они непрерывны вместе со своими производными внутри каждой однородной области, но могут претерпевать разрывы на границах раздела двух сред. В связи с этим представляется удобным решать уравнения Максвелла (1) - (4) в каждой области, ограниченной некоторой поверхностью раздела отдельно, а затем полученные решения объединять с помощью граничных условий. являются кусочно-непрерывными функциями координат, т.е. они непрерывны вместе со своими производными внутри каждой однородной области, но могут претерпевать разрывы на границах раздела двух сред. В связи с этим представляется удобным решать уравнения Максвелла (1) - (4) в каждой области, ограниченной некоторой поверхностью раздела отдельно, а затем полученные решения объединять с помощью граничных условий.
При нахождении граничных условий удобно исходить из интегральной формы уравнений аксвелла. Согласно уравнению (4) и теореме Остроградского-Гаусса:
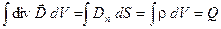 , (16) , (16)
где Q
– полный заряд внутри объёма интегрирования.
Рассмотрим бесконечно малый объём в виде цилиндра с высотой h
и площадью основания S
, расположенный в средах 1 и 2 (рис. 2).
 Соотношение (16) в этом случае можно записать виде: Соотношение (16) в этом случае можно записать виде:
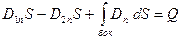 (17) (17)
здесь 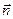 - нормаль к границе раздела двух сред, направленная из среды 2 в среду 1. Знак «минус» во втором слагаемом обусловлен тем, что внешняя нормаль - нормаль к границе раздела двух сред, направленная из среды 2 в среду 1. Знак «минус» во втором слагаемом обусловлен тем, что внешняя нормаль 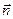 поверхности интегрирования в среде 2 направлена противоположно нормали поверхности интегрирования в среде 2 направлена противоположно нормали 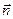 в среде 1. Пусть основание цилиндра стремится к границе раздела двух сред. Так как площадь боковой стремится к нулю, то в среде 1. Пусть основание цилиндра стремится к границе раздела двух сред. Так как площадь боковой стремится к нулю, то  , и поэтому (17) приобретёт вид: , и поэтому (17) приобретёт вид:
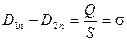 (18) (18)
где 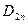 и и  - значения нормальных составляющих вектора - значения нормальных составляющих вектора 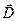 по разные стороны поверхности раздела; по разные стороны поверхности раздела; 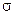 - поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества. Если поверхность раздела не заряжена, то в формуле (18) необходимо положить - поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества. Если поверхность раздела не заряжена, то в формуле (18) необходимо положить 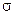 =0. Пользоваться понятием поверхностной плотности удобно тогда, когда избыточные (сторонние) заряды расположены в очень тонком слое вещества d, а поле рассматривается на расстояниях от поверхности r
>>d
. Тогда из определения объёмной плотности заряда =0. Пользоваться понятием поверхностной плотности удобно тогда, когда избыточные (сторонние) заряды расположены в очень тонком слое вещества d, а поле рассматривается на расстояниях от поверхности r
>>d
. Тогда из определения объёмной плотности заряда 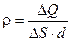 следует: следует:
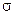 = = 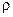 d
= d
= 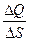 . .
Если учесть, что 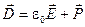 , а , а 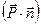 - поверхностная плотность поляризационных зарядов, то формулу (18) можно записать в виде: - поверхностная плотность поляризационных зарядов, то формулу (18) можно записать в виде:
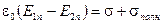
где 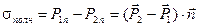 , а величина , а величина 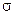 , которая входит в граничное условие (18), есть поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества. , которая входит в граничное условие (18), есть поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества.
Используя уравнение (2) и проводя аналогичные рассуждения, получаем граничное условие для вектора 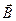 : :
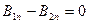 (19) (19)

Выражения (18) и (19) – граничные условия для нормальных составляющих векторов 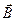 и и  . Чтобы получить условия для тангенциальных составляющих можно использовать уравнения (1) и (3). Умножим уравнение (3) скалярно на положительную нормаль . Чтобы получить условия для тангенциальных составляющих можно использовать уравнения (1) и (3). Умножим уравнение (3) скалярно на положительную нормаль 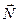 к поверхности S
, ограниченной контуром L
, имеющим вид прямоугольника (рис. 3). к поверхности S
, ограниченной контуром L
, имеющим вид прямоугольника (рис. 3).
Используя теорему Стокса, получим:
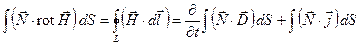
Перепишем это уравнение в виде:
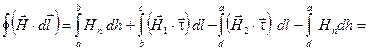
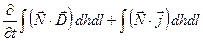 (20) (20)
Здесь 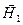 и и 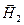 - значения вектора - значения вектора 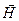 соответственно в средах 1 и 2, соответственно в средах 1 и 2, 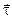 - единичный вектор, касательный к поверхности раздела, - единичный вектор, касательный к поверхности раздела, 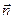 - нормаль к поверхности раздела, направленная из среды 2 в среду 1. - нормаль к поверхности раздела, направленная из среды 2 в среду 1.
Пусть теперь 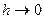 при малом, но фиксированном l
. Тогда при малом, но фиксированном l
. Тогда 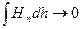 , , 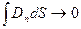 и соотношение (20) примет вид: и соотношение (20) примет вид:
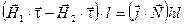
и после сокращения на l
имеем:
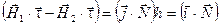
здесь 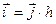 . Вектор . Вектор 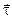 , как следует из рисунка 2, можно записать как в виде , как следует из рисунка 2, можно записать как в виде 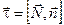 . Тогда . Тогда
предыдущее выражение можно записать, как
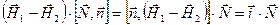 . .
Поскольку эта формула справедлива для любой ориентации поверхности , а следовательно, и
вектора  , то имеем , то имеем
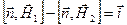 (21) (21)
В граничном условии (21) присутствует поверхностная плотность тока, избыточная по отношению к токам намагничивания. Если токи отсутствуют, то следует положить  =0. Учитывая, что =0. Учитывая, что 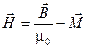 , а , а 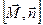 есть поверхностная плотность тока намагничивания, запишем формулу (21) в виде: есть поверхностная плотность тока намагничивания, запишем формулу (21) в виде:

где 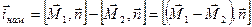 . .
Используя уравнение (1) и проводя аналогичные рассуждения, получаем граничные условия для вектора 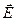 : :
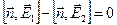 (22) (22)
Таким образом, уравнения Максвелла (1) - (4) должны быть дополнены граничными условиями (18), (19), (21) и (22). Эти условия означают непрерывность тангенциальных составляющих вектора 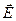 (22) и нормальной составляющей вектора (22) и нормальной составляющей вектора 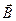 (19) при переходе через границу раздела двух сред. Нормальная составляющая вектора (19) при переходе через границу раздела двух сред. Нормальная составляющая вектора 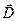 при переходе через границу раздела испытывает скачок, тангенциальная составляющая вектора при переходе через границу раздела испытывает скачок, тангенциальная составляющая вектора 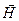 , если имеются поверхностные токи (21). , если имеются поверхностные токи (21).
Ещё одно граничное условие можно получить, используя уравнение непрерывности (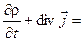 0) и уравнение (4), из которых следует: 0) и уравнение (4), из которых следует:

Так как граничное условие (19) является следствием уравнения (2), то по аналогии находим:
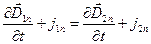 (23) (23)
Если же на поверхности раздела нет зарядов, поверхностная плотность которых зависит от времени, то из (18) и (23) следует непрерывность нормальных составляющих плотности тока:
 . .
Итак, граничные условия на поверхности раздела двух сред имеют вид:
 ; ; 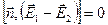
(24)
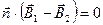 ; ; 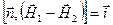
где  - нормаль к границе раздела, направленная из среды 2 в среду 1, и должны выполняться в любой момент времени и в каждой точке поверхности раздела. - нормаль к границе раздела, направленная из среды 2 в среду 1, и должны выполняться в любой момент времени и в каждой точке поверхности раздела.
3. Уравнения Максвелла в системе уравнений магнитостатики и электростатики
Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4).
В случае стационарных электрических и магнитных полей (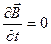 и и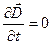 ) система уравнений Максвелла (1) – (4) распадается на систему ) система уравнений Максвелла (1) – (4) распадается на систему
уравнений электростатики
:
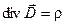 , , 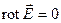 , , 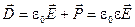 (25) (25)
и уравнений магнитостатики
:
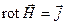 , , 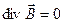 , , 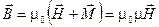 , (26) , (26)
а граничные условия остаются те же.
4. Пример
В качестве примера решения электростатических задач можно вычислить электрическое поле, создаваемое диэлектрическим шаром радиуса R, находящемся в однородном электрическом поле  . Уравнения электростатики в диэлектрике (25) при . Уравнения электростатики в диэлектрике (25) при 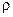 =0 имеют вид: =0 имеют вид:
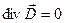 , , 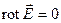 , ,  (27) (27)
Из этих уравнений следует, сто потенциал электростатического поля удовлетворяет уравнению
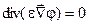 (28) (28)
причём 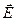 = - = -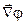 , , 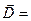 - -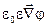 . В однородном диэлектрике . В однородном диэлектрике 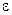 =const , поэтому уравнение (27) переходит в обычное уравнение Лапласа =const , поэтому уравнение (27) переходит в обычное уравнение Лапласа 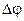 =0. =0.
Граничное условия (24), выражающее непрерывность вектора индукции, записывается следующим образом:
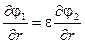 при r
=R
(29) при r
=R
(29)
Здесь 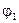 – решение уравнения вне сферы, а – решение уравнения вне сферы, а 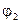 – внутри сферы. Вместо граничного условия непрерывности тангенциальных составляющих электрического поля можно использовать эквивалентное ему условие непрерывности потенциала – внутри сферы. Вместо граничного условия непрерывности тангенциальных составляющих электрического поля можно использовать эквивалентное ему условие непрерывности потенциала
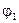 = =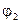 (30) (30)
Это условие можно получить, рассматривая интеграл 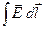 по контуру, изображенному на рис. 2. Воспользовавшись теоремой Стокса и уравнением по контуру, изображенному на рис. 2. Воспользовавшись теоремой Стокса и уравнением  , находим , находим
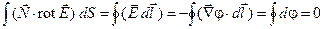
Так как интеграл по любому замкнутому контуру равен нулю, то это значит, что функция 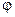 непрерывна, откуда и следует условие (30). Из (30) очевидно так же, что непрерывна, откуда и следует условие (30). Из (30) очевидно так же, что
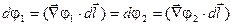
где элемент 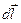 направлен касательно к границе раздела. Из этого равенства следует, что тангенциальные компоненты вектора направлен касательно к границе раздела. Из этого равенства следует, что тангенциальные компоненты вектора 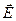 также непрерывны. также непрерывны.
Для решения поставленной задачи используем сферическую систему координат, полярная ось которой (ось z
) совпадает с направлением напряжённости однородного внешнего электрического поля 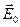 . .
Поскольку на достаточно большом удалении от диэлектрического шара электрическое поле не искажается наличием этого шара, то потенциал 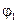 должен удовлетворять условию должен удовлетворять условию
  при при 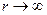 . .
Из соображений симметрии ясно, что потенциал не должен зависеть от азимутального угла, поэтому решение уравнения Лапласа запишем в виде разложения по полиномам Лежандра 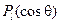 : :
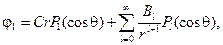 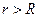 , ,
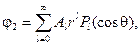 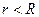 . .
Здесь потенциал нормирован так, чтобы 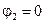 при при 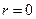 . Так как . Так как  , то из условия на бесконечности находим , то из условия на бесконечности находим 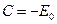 . .
Воспользуемся теперь граничными условиями (29) и (30):
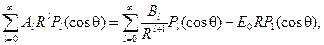
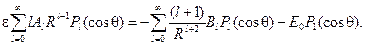
Приравнивая коэффициенты при одинаковых полиномах Лежандра, получаем
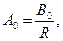 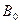 =0 при (l
=0), =0 при (l
=0),
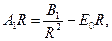 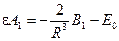 при (l
=1), при (l
=1),
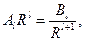 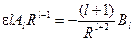 при (l
>1). при (l
>1).
Из этих уравнений находим
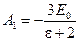 , , 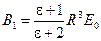 . .
Все остальные коэффициенты равны нуля, если 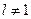 . .
Таким образом, решение задачи имеет вид:
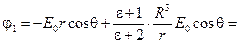
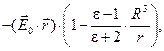 (30) (30)
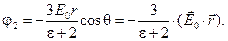
Используя формулу 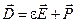 , вычислим вектор поляризации диэлектрической сферы , вычислим вектор поляризации диэлектрической сферы

С помощью вектора поляризации формулы (30) можно записать в виде:
 (31) (31)
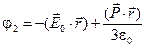 (32) (32)
где 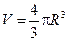 - объём сферы. - объём сферы.
Первые два слагаемых в (31) и (32) представляют собой потенциал однородного внешнего поля, создаваемого внешними источниками. Вторые – это потенциал электрического поля, создаваемого электрическим шаром, поляризованным внешним полем. Вне сферы – это потенциал диполя с дипольным моментом 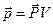 . Внутри сферы поляризованный шар создаёт однородное электрическое поле с напряжённостью . Внутри сферы поляризованный шар создаёт однородное электрическое поле с напряжённостью
 (33) (33)
Полная напряжённость внутри шара
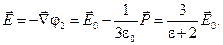 (34) (34)
Таким образом, электрическое поле внутри шара не зависят от радиуса шара и ослаблено на значение поля 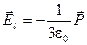 , которое называется деполяризующим полем. Возникновение деполяризующего поля есть частный случай явления экранировки внешнего поля связанными или свободными зарядами. , которое называется деполяризующим полем. Возникновение деполяризующего поля есть частный случай явления экранировки внешнего поля связанными или свободными зарядами.
5. Приложение.
1. Формула Остроградского – Гаусса.
Пусть f
(x
, y
, z
) - некоторая функция , а S
- замкнутая поверхность, ограничивающая объём V
. На отрезке 1-2
(рис. 4), параллельном оси X
, f
- является функцией одного аргумента x
. Интегрируя вдоль этого отрезка получим:
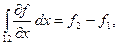
где 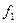 и и 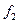 - значения функции f
на концах рассматриваемого промежутка. - значения функции f
на концах рассматриваемого промежутка.
Построим теперь бесконечно узкий цилиндр, одной из образующих которого является отрезок 1 2
. Пусть dσ
- площадь поперечного сечения его (величина положительная). Умножая предыдущее соотношение на dσ
. Так как dσdx
есть элементарный объём dV
, заштрихованный на рисунке, то в результате получится:

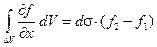 , ,
где dV
– часть объёма V
, вырезаемого из него поверхность цилиндра. Пусть dS
1
и dS
2
эле -ментарные площадки, вырезаемые тем же цилиндром на поверхности S
, а 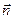 1
и 1
и 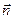 2
– 2
–
единичные нормали к ним, проведенные наружу от поверхности S
. Тогда:
dσ
= d
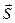 2 2
 2х
= - d 2х
= - d
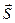 1 1
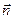 1х
, 1х
,
а поэтому: 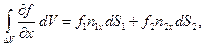
или короче: 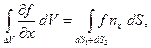 где поверхностный интеграл распространён на сумму площадок dS
1
и dS
2
. Весь объём V
можно разделить на элементарные цилиндры рассматриваемого вида и написать для каждого из них такие же соотношения. Суммируя эти соотношения, получим: где поверхностный интеграл распространён на сумму площадок dS
1
и dS
2
. Весь объём V
можно разделить на элементарные цилиндры рассматриваемого вида и написать для каждого из них такие же соотношения. Суммируя эти соотношения, получим:
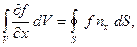 (35) (35)
Интеграл справа распространён по всему объёму V
, справа – по поверхности S
, ограничивающей этот объём. Аналогичные соотношения можно написать для осей Y
и Z
.
Возьмём теперь произвольный вектор  и применим к его компонентам соотношение (35). Получим: и применим к его компонентам соотношение (35). Получим:
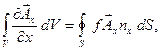
и аналогично для компонент A
y
и A
z
. Складывая эти соотношения, найдём:
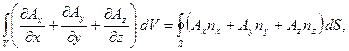
или:
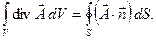
Эту формулу Остроградского – Гаусса
можно также записать в виде:
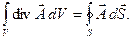
Смысл её заключается в том, что полный поток вектора  через некоторую поверхность
S равен суммарной алгебраической мощности источников, порождающих векторное поле
. через некоторую поверхность
S равен суммарной алгебраической мощности источников, порождающих векторное поле
.
Если объём V
бесконечно мал, то величина div внутри него может считаться постоянной. Вынося её за знак интеграла и переходя к пределу V
→ 0, получим: внутри него может считаться постоянной. Вынося её за знак интеграла и переходя к пределу V
→ 0, получим:
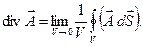
Предельный переход надо понимать в том смысле, что область V
должна стягиваться в точку, т.е. размеры этой области должны беспредельно уменьшаться по всем направлениям. Эти рассуждения показывают, что величина, стоящая в правой части вышеуказанной формулы, не зависит от формы поверхности S
, стягиваемой в точку. Поэтому это выражение можно принять за исходную формулировку дивергенции. Такое определение обладает преимуществом, потому что оно инвариантно, т.е. никак не связано с выбором координат.
2. Формула Стокса.
По определению ротор (вихрь) некоторого вектора  : :
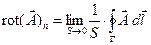 (36) (36)
Зная ротор вектора  в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру 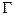 , ограничивающему S
, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы , ограничивающему S
, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы  . Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора . Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора 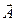 по контуру, ограничивающему по контуру, ограничивающему 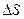 , может быть представлена в виде. , может быть представлена в виде.
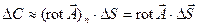 (37) (37)
где  - положительная нормаль к элементу поверхности - положительная нормаль к элементу поверхности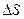 . .
Зная, что циркуляция по некоторому контуру равна сумме циркуляций по контурам, содержащиеся в данном, можно просуммировать выражение (37) по всем  , и тогда получим циркуляцию вектора , и тогда получим циркуляцию вектора  по контуру по контуру 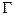 , ограничивающему S
: , ограничивающему S
:
  . .
Осуществив предельный переход, при котором все 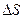 стремиться к нулю (число их при этом неограниченно растёт, придём к формуле: стремиться к нулю (число их при этом неограниченно растёт, придём к формуле:
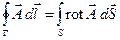 (38) (38)
Соотношение (38) носит название теоремы Стокса.
Смысл её состоит в том, что циркуляция вектора  по произвольному контуру по произвольному контуру 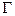 равна потоку вектора равна потоку вектора 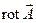 через произвольную поверхность
S , ограниченную данным контуром
. через произвольную поверхность
S , ограниченную данным контуром
.
6. Список использованной литературы
- Федорченко А. М. Классическая электродинамика. – К.: Вища школа, 1988. – 280 с.
- Сивухин Д. В. Общий курс физики. Электричество. – М.: Наука, 1983. – 688 с.
- Савельев И. В. Курс обшей физики. 3 том. – М.: Наука, 1988. – 496 с.
|