| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
Математический факультет
Кафедра математического анализа и методики преподавания математики
Выпускная квалификационная работа
ОБУЧЕНИЕ РЕШЕНИЮ ЗАДАЧ НА ПРОЦЕНТЫ
В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ
(по учебному комплекту под редакцией Г.В. Дорофеева)
Выполнила студентка V курса математического факультета Киселёва Е.Н.
/ подпись/
Научный руководитель
к.п.н., доцент Крутихина М.В.
/ подпись/
Рецензент
к.п.н., доцент Ситникова И.В.
/ подпись/
Допущена к защите в ГАК
Зав. кафедрой Крутихина М.В.
« » 2004 г.
Декан факультета Варанкина В.И.
« » 2004 г.
КИРОВ
2004
Содержание
ВВЕДЕНИЕ..............................................................................................................3
Глава I. ТЕОРИТИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ ПРОЦЕНТОВ В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ. 5
§ 1. Особенности учебного комплекта по математике под редакцией Г.В. Дорофеева. 5
§ 2. Понятие процента, основные задачи на проценты. 8
§ 3. Изучение темы «Проценты» в современной школе. 12
Глава II. МЕТОДИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ ПРОЦЕНТОВ ПО УЧЕБНОМУ КОМПЛЕКТУ ПОД РЕДАКЦИЕЙ Г.В. ДОРОФЕЕВА. 21
§ 1. Методические рекомендации изложения темы «Проценты » по учебному комплекту под редакцией Г.В. Дорофеева для V – IX классов. 21
§ 2. Методические рекомендации для проведения урока «Простые проценты» по учебнику «Математика. Алгебра. Функции. Анализ данных» 9 кл. под редакцией Г.В. Дорофеева. 34
§ 3. Методические рекомендации к проведению факультатива «Задачи на проценты» в IX классе. 39
§ 4. Опытное преподавание. 46
ЗАКЛЮЧЕНИЕ. 48
СПИСОК ЛИТЕРАРУРЫ.. 49
В
ВЕДЕНИЕ
В настоящее время уделяется большое внимание школьному образованию как первой ступени образовательного процесса. Одна из важнейших его задач – обеспечить учащимся глубокие и прочные знания, а также умение рационально применять их в учебной и практической деятельности.
Большое практическое значение имеет умение решать задачи на проценты, потому что понятие процента широко используется как в реальной жизни, так и в различных областях науки.
В школьном курсе эта тема изучается в V – VI классе, но в силу возрастных особенностей школьников не может быть полностью освоена. Далее этому вопросу не уделяется значительного внимания. Задачи на проценты становятся прерогативой химии, которая внедряет свой взгляд на проценты, а в математике их место только в рамках задач на повторение и задач повышенной трудности. Таким образом, учениками забываются проблемы универсальности процентов и разнообразия сфер их применения. В связи с этим является актуальным вопрос о том, чтобы задачи на проценты заняли достойное место в VII – IX классах. В этот период школьники изучают различные виды уравнений и их систем, закрепление которых ведется на текстовых задачах, а присутствие процентов в содержании текстовых задач дает возможность связать абстрактные математические понятия с реальной жизнью.
Такая тенденция прослеживается в учебном комплекте по математике под ред. Г.В. Дорофеева. В VI классе авторы комплекта уделяют внимание формированию понятия процента, а в VII – IX классах рассматривают основные задачи на проценты и различные способы их решения. Причем следует отметить большое разнообразие задач. Но для такого богатого материала не имеется четкой методики изучения, так как комплект еще «молодой» и особенно в школах не распространен.
Поэтому цель
данной работы состоит в разработке методических рекомендаций по изучению темы «Проценты» по учебникам [20], [15], [18],[17], [16].
Объектом
исследования является обучение математике в V – IX классов.
Предмет
исследования – обучение решению задач на проценты в курсе алгебры VII – IX классов.
В данной работе выдвинута следующая гипотеза
: Обучение решению задач на проценты будет более эффективным, если:
1. Формирование понятия процента начать в V – VI классе.
2. Рассматривать различные типы задач на проценты в течение всего курса алгебры VII – IX класса.
3. Использовать символическую наглядность, как при формировании понятия процента, так и при изучении основных типов задач.
Задачи данной работы:
1. Выявить особенности учебного комплекта по математике под ред. Г.В. Дорофеева.
2. Провести анализ содержания данного комплекта с точки зрения изложения темы «Проценты».
3. Разработать методические рекомендации по изучению темы «Проценты».
4. Осуществить опытное преподавание.
Для достижения поставленных целей, проверки гипотезы и решения сформулированных выше задач были использованы следующие методы
исследования:
1. Изучение учебно-методической и математической литературы.
2. Анализ школьных учебников.
3. Опытное преподавание.
4. Наблюдение во время проведения занятий с учащимися.
Глава
I. ТЕОРИТИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ ПРОЦЕНТОВ В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ.
§ 1. Особенности учебного комплекта по математике под редакцией Г.В. Дорофеева.
В учебный комплект по математике под редакцией Г.В. Дорофеева[1]
входят учебники [20], [15], [18],[17], [16]. Это комплект нового поколения. В нем учтены результаты опыта преподавания математики последних десятилетий, а также отражены современные методические и педагогические тенденции. Содержание комплекта полностью соответствует современным образовательным стандартам. Он рекомендован Министерством общего и профессионального образования Российской Федерации для преподавания математики в средней школе.
Основные идеи этого курса – это общекультурная ориентация содержания, интеллектуальное развитие учащихся средствами математики на материале, отвечающем интересам и возможностям детей. Одним из главных отличий данного комплекта является то, что большое внимание уделяется арифметике, формированию вычислительной культуры в ее современном понимании. Это прикидка, оценка и проверка результатов действий. Сделан упор на обучение арифметическим, логическим приемам решения текстовых задач.
В учебниках комплекта принята следующая система подачи материала. Теоретический материал каждой главы разбит на пункты, которые завершаются перечнем упражнений. Предложенные упражнения имеют два уровня сложности: первый ориентирован на базовый уровень обучения, второй содержит развивающие задания. В конце главы выделен пункт «Для тех, кому интересно», в которых предлагается материал, не предусмотренный школьной программой, но предлагаемый на школьных олимпиадах. Это позволяет сделать знания учащихся более прочными, пробудить интерес к математике. Это уравнения с параметрами, делимость натуральных чисел, примеры использования комбинаторного правила умножения и другие вопросы математики. Для более успешного усвоения материала в каждую главу включены вопросы для повторения и задачи для самопроверки. К каждому учебнику разработан набор справочно-методической литературы (рабочие тетради, сборники дидактических материалов), облегчающих работу, как учителю, так и ученику.
Рабочая тетрадь применяется преимущественно на начальных этапах изучения темы. Туда включены задания, которые позволяют организовать разнообразную практическую деятельность (вычеркнуть, дорисовать, закрасить). Это освобождает детей от работы непринципиального характера, позволяет увеличить объем учебной работы и сосредоточить внимание на главном.
Дидактические материалы содержат дополнительный набор упражнений по арифметике, алгебре, анализу данных, организованных в виде самостоятельной работы с заданиями разного уровня сложности. Материал может быть использован на различных этапах изучения темы и для различных групп учащихся. В конце сборника помещены материалы для внеклассной работы.
Учебники [20], [15] заложили одну из первых «сквозных» линий, которую через все классы проводит один авторский коллектив (далее он несколько изменяется, но руководство Г.В. Дорофеева остается неизменным; последние учебники этой линии для X – XI класса еще ожидаются). Наличие «сквозной» авторской линии дает некоторые преимущества в плане сохранения авторских подходов и преемственности между блоками классов. В данных учебниках принят естественный порядок изучения дробей: сначала обыкновенные, потом десятичные. Вопрос о знаке числа изучается сначала на целых числах, что методически и педагогически правильнее. Особенно выделяется наглядно-деятельностная геометрия. Есть линия «Анализ данных». Не смотря на то, что арифметическая линия не завершена по сравнению с традиционно принятым объемом содержания, изучаемого в V – VI классах, это не препятствует обучению в рамках той же авторской линии.
Учебники [18], [17], [16] являются непосредственным продолжением комплекта [20], [15]. В них получают дальнейшее развитие арифметическая, алгебраическая и вероятностно-статистическая линии курса. Некоторый материал, изучавшийся раньше в V – VI классах перенесен в следующие классы. В рамках одной линии учебников такой подход не нарушает целостности изучения материала. В содержание курса алгебры VII – IX классов включен блок арифметических вопросов. Уделено внимание дальнейшему развитию вычислительной культуры школьников, обучению различным приемам выполнения действий с дробями, в том числе с использованием калькулятора, вычислению процентов и вероятностно-статистических характеристик. В VII классе рассмотрены также практически значимые вопросы об отношении, пропорции, прямой и обратной пропорциональности. В VIII классе уделено внимание формированию вычислительных умений извлечения квадратного корня и отработке его простейших свойств. Отработка этих умений проводится на арифметических выражениях без использования символики. После этого в качестве обобщения авторы предлагают алгебраический подход к понятию корня. При изучении прогрессий в IX классе сделан акцент на их практическое применение, поэтому для изучения предложена тема «Простые и сложные проценты».
Отбор учебного материала и выбор методических подходов в учебниках осуществляется с учетом возможностей и особенностей детей данного возраста, что способствует более глубокому и осмысленному пониманию данных вопросов. В связи с этим авторы курса переносят рассмотрение некоторых тем на более поздние сроки. Это позволяет изучить практически значимый и интересный для детей материал, который позволяет говорить о математике, как о части общечеловеческой культуры.
В настоящее время в школе не распространен подход целостного изучения математики V – IX классов, поэтому этот комплект можно назвать комплектом нового поколения.
§ 2. Понятие процента, основные задачи на проценты.
Слово «процент» происходит от латинского pro
centum
, что буквально означает «на сотню», «со ста» или «за сотню». В популярной литературе возникновение этого термина связывается с внедрением в Европе десятичной системы счисления в XV в. Но идея выражения частей целого постоянно в одних и тех же величинах, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти». Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню.
По-видимому, процент возник в Европе вместе с ростовщичеством. Есть мнение, что понятие процент ввел бельгийский ученый Симон Стевин. В 1584 г. он опубликовал таблицы процентов. Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Интересно происхождение обозначения процента. Существует версия, что знак % происходит от итальянского pro
cento
(сто), которое в процентных расчетах часто сокращенно писалось cto
. Отсюда путем дальнейшего сокращения в скорописи буква t
превратилась в наклонную черту (/), возник современный знак процента (см. схему 1).
 Схема 1 Схема 1
Также есть предположение, что знак % возник в результате опечатки. В Париже в 1685 г. была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик напечатал знак %.
Сейчас проценты употребляются для сравнения однородных положительных количеств. Один процент – это по определению одна сотая: 1%= .
Соответственно, p
%= .
Соответственно, p
%=
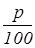 .
Один процент от количества А – это, по определению, одна сотая часть количества А:
.
Один процент от количества А – это, по определению, одна сотая часть количества А:
1%
от А
равен 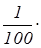 А
.Соответственно, p
%
от А
равен А
.Соответственно, p
%
от А
равен 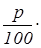 А
. А
.
Все задачи на проценты можно разделить на две основные группы.
Первая группа
задач относится к той ситуации, когда даны количество А
и некоторый процент p
. Требуется найти количество, которое этот процент выражает.
Вопрос К1
. Каково количество, составляющее p
%
от А
?
Формула ответа: 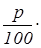 А
. А
.
Обсуждение решения: нужно обсудить, что принимается за базу в 100% .
Пример:
В городе N состоялись выборы в городскую думу, в которых приняли участие 75% избирателей. Только 10% от числа принявших участие в выборах отдали свои голоса партии «зеленых». Сколько жителей проголосовали за эту партию, если всего в городе 1 миллион избирателей?
Решение. Здесь нужно дважды применить формулу ответа на вопрос К1. По условию, в выборах приняли участие 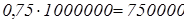 чел. От них 10% - это чел. От них 10% - это 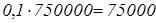 . .
Ответ: 75000.
Вопрос К2
. Каково количество, p
%
от которого есть А
?
Формула ответа: 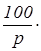 А
. А
.
Обсуждение. Вопросы К1 и К2 родственны. Пусть искомое количество (в данном случае стопроцентная база) есть x. Тогда мы находимся в ситуации вопроса К1: А=
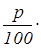 x
. Отсюда получаем формулу ответа на вопрос К2. Можно воспользоваться другим способом рассуждения при ответе на вопрос К2: если на А
приходится p
%
, то один процент от неизвестного количества есть x
. Отсюда получаем формулу ответа на вопрос К2. Можно воспользоваться другим способом рассуждения при ответе на вопрос К2: если на А
приходится p
%
, то один процент от неизвестного количества есть 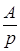 , соответственно неизвестное количество есть 100 , соответственно неизвестное количество есть 100
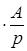 . .
Пример:
При помоле пшеницы получается 80% муки. Сколько пшеницы нужно смолоть, чтобы получить 480 кг пшеничной муки?
Решение:
По формуле К2 искомое количество пшеницы есть 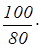 480=600 кг 480=600 кг
Ответ: 600 кг.
Вопрос К3
. Каково количество, большее чем А
, на p
%
?
Формула ответа: 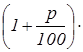 А
. А
.
Обсуждение. В данном случае стопроцентная база – это А
. Разница между неизвестным количеством и базой по условию составляет p
%
, что по формуле ответа на вопрос К1 дает 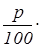 А
. В результате искомое количество есть А+ А
. В результате искомое количество есть А+
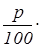 А=
А=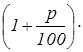 А
. А
.
Вопрос К4
. Каково количество, меньшее чем А
, на p
%
?
Формула ответа: 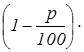 А
. А
.
Обсуждение. Аналогично предыдущему случаю. Если ответ на данный вопрос приводит к отрицательному числу, то искомое количество считают несуществующим, а сам вопрос некорректным.
Вторая группа
задач освещает обратную операцию – вычисление процентов по известным количествам.
Вопрос П1
. Сколько процентов составляет А
от В
?
Формула ответа: 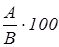 %
. %
.
Обсуждение. Нужно обратить внимание на то, что является стопроцентной базой (в данном случае – это В
).
Пример:
В одном городе Канады 70% жителей знают французский язык и 80% - английский язык. Сколько процентов жителей этого города знают оба языка (если учесть, что каждый житель города знает хотя бы один из двух языков)?
Алгебраическое решение: Пусть x
жителей знают только английский, y
– только французский, z
– оба языка. Тогда можно дважды применить формулу, соответствующую вопросу П1.
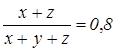 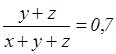
Сложив оба эти равенства, получим
1+

Ответ: 50%.
Геометрическое решение. Разместим всех жителей города на отрезке так, что знающие английский язык стоят на отрезке слева, а знающие французский – справа. Если этот отрезок – 100%, то общая часть этих множеств есть отрезок [30%,80%] «протяженностью» в 50% (см. рис 1.).

Рис 1.
Вопрос П2.
На сколько процентов А
больше чем В
?
Формула ответа: 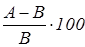 %
. %
.
Обсуждение. Как и при обсуждении вопроса П1 нужно определить стопроцентную базу (в данном случае – это В
).
Вопрос П3
. На сколько процентов А
меньше, чем В
?
Формула ответа: 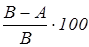 %
. %
.
Обсуждение. Конструкция ответа аналогична предыдущему случаю.
Следует отметить, что решение данной группы задач можно проводить как алгебраическим, так и геометрическим способом.
Таким образом, можно сказать, что задачи на проценты очень разнообразны, а понятие процента используется в различных областях науки и практики.
Понятие процента имеет широкое практическое применение, поэтому оно является обязательной частью школьной программы по математике. Школьники должны научится решать основные задачи на проценты, представлять их в виде десятичных и обыкновенных дробей.
Традиционно тема «Проценты» изучается в рамках младших классов среднего звена. Можно выделить несколько подходов к изучению данной темы.
Первый подход.
Рассмотрение процентов ведется как отдельная тема, без опоры на дроби. Нахождение нескольких процентов от числа осуществляется в два действия. Изучение дробей ведется отдельной темой, гораздо позже задач на проценты. Таким образом, обучение идет от частного к общему, что менее эффективно и дает меньше возможностей для развития обучаемого.
Второй подход.
Задачи на проценты осваиваются как частный случай задач на дроби и все приемы решения переносятся на них, то есть изучение идет от общего случая – задач на дроби, к частному. В большинстве современных учебников реализован второй подход.
Рассмотрим более подробно изучение данной темы в некоторых современных учебниках, рекомендованных Министерством Образования России на 2003/2004 учебный год для преподавания математики в основной школе.
По учебникам [19], [21] тема «Проценты» изучается в V классе. Перед введением понятия «процент» автор предлагает рассмотреть примеры:
«Сотую часть центнера называют килограммом, сотую часть метра – сантиметром, сотую часть гектара – акром. Принято называть сотую часть любой величины процентом».
Рассматриваются три основные задачи на проценты:
Задача вида К1
.
Пример 1: Бригада рабочих за день отремонтировала 40% дороги, имеющей длину 120 м. Сколько метров дороги было отремонтировано бригадой за день?
Решение:
120 м составляет 100%
1) 120:100 =1,2 м составляет 1%.
2) 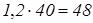 м отремонтировано бригадой за день. м отремонтировано бригадой за день.
Ответ: За день бригада отремонтировала 48 м дороги.
Задача вида К2.
Пример 2: Ученик прочитал 72 страницы, что составляет 30% числа всех страниц книги. Сколько страниц в книге?
Решение:
Неизвестное число – 100%.
1) 72:30=2,4 страницы составляет 1%.
2) 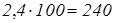 страниц составляет 100%. страниц составляет 100%.
Ответ: В книге 240 страниц.
Задача вида П1
.
Пример 3: В классе из 40 учащихся 32 правильно решили задачу. Сколько процентов учащихся правильно решили задачу?
Решение:
40 учащихся составляют 100%.
1) 40:100=0,4 составляет 1%.
2) 32:0,4=80; 32 ученика составляют 80%.
Ответ: 80% учащихся правильно решили задачу.
Однако эти виды задач не выделяются, так как в качестве основного способа решения задач на проценты принят способ приведения к единице. Он обладает определенными преимуществами:
а) проще для выполнения вычислений;
б) приучает учащихся к выделению числа, принимаемого за 100%;
в) требует проведения в процессе решения конкретной задачи соответствующих рассуждений, которые не включают запоминания правил решения того или иного вида задач на проценты.
Учебник предполагает решать некоторые задачи на проценты с помощью уравнений. Эта рекомендация относится по существу к двум видам задач: нахождение числа по данному числу его процентов и нахождение процентного отношения двух чисел. Опыт преподавания математики в V классе показывает, что учащиеся сталкиваются с определенными трудностями в процессе решения задач на проценты, что связано в основном с недостаточной осознанностью учащимися способа приведения к единице. Поэтому отработка сущности этого способа в два действия имеет решающее значение в обучении решению задач на проценты, особенно на начальном этапе усвоения знаний. Задачи, рассмотренные в примерах 2 и 3, могут быть решены с помощью уравнений. В V классе решение задач с помощью уравнений вызывают у учащихся значительные трудности.
Эта тема является одной из последних в курсе V класса. Далее авторы специально к теме не возвращается. Это не очень удачно, так как тема объективно трудная.
Несколько другой подход к этой теме в учебниках [22] [23]. Изучение процентов начинается в конце V класса. Авторы определяют процент, как иное название одной сотой. «Мы знаем, что одна вторая иначе называется половиной, одна четвертая – четвертью, три четвертых – тремя четвертями. Особое название имеет и одна сотая: одна сотая называется процентом». Учащиеся рассматривают только два вида задач:
Задача вида К1
.
Пример 4. В школе 800 учащихся, 15% из них за четверть получили пятерки по математике. Сколько учеников получили пятерки по математике?
Решение:
Найдем вначале один процент, или одну сотую, от числа уча
щихся.
800: 100=8.
Чтобы найти 15%, нужно выполнить умножение:
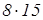 =120. =120.
Ответ: 120 учеников получили пятерки.
Большое внимание уделяется связи дробей (десятичных и обыкновенных) и процентов.
Задача вида П1
.
Пример 5. Сколько процентов от 1 м составляет 1см, 9 см, 0,15 м?
В VI классе авторы снова возвращаются к этой теме. Учащиеся повторяют материал, изученный в V классе, и рассматриваются новые задачи. При этом для каждого вида задач проводится аналогия с действиями над десятичными и обыкновенными дробями, формулируется правило:
Для задачи вида К1.
«1) выразить проценты обыкновенной или десятичной дробью;
2) умножить данное число на эту дробь»
А также для задачи вида К2.
«1) выразить проценты обыкновенной или десятичной дробью;
2) разделить данное число на эту дробь»
Пример 6. За контрольную работу по математике отметку «4» получили 9 учеников. Это составляет 36% от всех учащихся класса. Сколько учащихся в классе?
Решение:
Выразим проценты обыкновенной или десятичной дробью: 36%= =0,36. =0,36.
Воспользуемся правилом нахождения числа по его дроби:
9: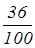 = =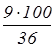 =25 или 9:0,36=25 =25 или 9:0,36=25
Ответ: в классе было 25 учащихся.
Далее рассматривается задача вида П1
.
Сначала учащиеся рассматривают выражение частного двух чисел в процентах: «чтобы выразить частное в процентах, нужно частное умножить на 100 и к полученному произведению приписать знак процента».
Только после этого они переходят к решению задачи П1
.
«Для этого нужно
1) первое число разделить на вторе;
2) полученное частное выразить в процентах»
Пример 7. В классе 25 учащихся, из них 20 пионеров. Сколько процентов составляют пионеры?
Решение:
Для решения нужно частное 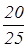 выразить в процентах. выразить в процентах. 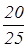 =0,8=80%. =0,8=80%.
Ответ: пионеры составляют 80%.
В конце темы рассматривается задача вида П2
и П3
.
«… чтобы узнать, на сколько процентов увеличилась или уменьшилась данная величина, необходимо найти:
1) на сколько единиц увеличилась или уменьшилась эта величина;
2) сколько процентов составляет полученная разность от первоначального значения величины»
Пример 8. До снижения цен холодильник стоил 250р., после снижения – 230 р. На сколько процентов снизилась стоимость холодильника?
Решение:
Узнаем, на сколько рублей изменилась цена холодильника: 250-230=20 р.
Найдем, сколько процентов составляет полученная разность от первоначальной стоимости холодильника: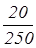 =0,08=8% =0,08=8%
Ответ: стоимость холодильника понизилась на 8%.
Правила ограничивают учащихся, не дают им рассуждать над решением. Поэтому каждая задача на проценты становится алгоритмом и вызывает затруднения, если правило забыто. Решение задач в данном курсе арифметическое. Использование уравнений при решении начинается лишь в конце года только в сложных задачах. Следовательно, не каждый ученик сможет овладеть этим умением. Поэтому нужно включить задачи на проценты при изучении уравнений.
В учебниках [7], [8] понятие процента также изучается в конце V класса. Перед введением определения рассматриваются примеры употребления понятия «процент»:
«Всхожесть семян составляет 98 процентов; в выборах президента России приняли участие 65 процентов избирателей… ». Процент определяется как обозначение сотой доли. В V классе авторы рассматривают только два вида задач: задачи вида К1
и К2
. Решение этих задач осуществляется арифметическим способом. Большое внимание уделяется вопросу, какую величину взять за 100%.
Далее тема «Проценты» изучается в VI классе. Здесь рассматриваются те же виды задач, но решение осуществляется уже алгебраическим способом (составление линейных уравнений). Авторы формулируют правила нахождения части от целого и целого по его части:
«1) чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь (соответствующее этой части);
2) чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую ей дробь».
После этого тема не рассматривается.
Несколько другой подход в учебниках [2], [3]. Проценты начинают изучаться в начале VI класса. Вводится понятие процента как одной сотой части числа (величины). Рассматриваются задачи трех типов:
а) нахождение процентов от данного числа К1
.
Сначала рассматривается нахождение 1% от данного числа. Затем - нахождение произвольного числа процентов.
б) нахождение числа по данному числу его процентов К2
.
Также в первую очередь обсуждается, как найти число, 1% которого известен. Затем эта задача рассматривается для любого произвольного числа процентов.
в) нахождение процентного отношения двух чисел П1
. Авторы формулируют правило «Чтобы отношение двух чисел выразить в процентах, можно это отношение умножить на 100»
Все три типа задач решаются сначала арифметическим способом, а затем их решают, на основе свойств пропорциональности.
Пример 9. Найти 8% от 35.
Решение: Пусть x – искомое число, тогда:
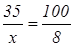 , x
= , x
=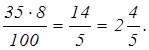 
Ответ: 2
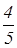
Рассматриваются также задачи, в которых нужно увеличить (уменьшить) число на некоторое число процентов К3
и К4.
Проценты также используются при изучении диаграмм.
В середине учебного года авторы снова предлагают вернуться к понятию процента. Они хотят установить связь между десятичными дробями и процентами, вспоминают ранее изученный материал и предлагают более сложные задачи.
Пример 10.
Цену товара увеличили на 10%, затем еще на 10%. На сколько процентов увеличили цену товара за два раза?
Здесь же рассматриваются задачи на смеси и сплавы (этот параграф отмечен, как параграф повышенной трудности). Мне кажется, что задачи такого типа для шестиклассников сложны. Поэтому не каждый учитель захочет рассматривать такие сложные задачи со всем классом и очень важный пласт задач останется не рассмотренным. Но это очень важные задачи, которым следует уделить должное внимание, возможно, в старшем возрасте.
В этом комплекте также уделяется внимание работе с калькулятором при решении задач на проценты. Данному вопросу посвящен отдельный параграф и разработана система упражнений.
В старших классах тема проценты рассматривается в рамках задач на повторение и задач повышенной трудности. В старших классах операции с процентами становятся прерогативой химии, которая внедряет свой взгляд на проценты. Поэтому вопросы универсальности процентов и разнообразия сфер их применения постепенно забываются учащимися.
Покажем, как предлагается изучать этот материал в учебных комплектах по математике для V-VI класса под ред. Г.В.Дорофеева и И.Ф. Шарыгина и для VII – IX класса под ред. Г.В.Дорофеева.
Прежде всего, нужно отметить, что при изложении темы «Проценты» реализуются многие общие методические особенности, характерные для курса в целом. Тема разворачивается по спирали и изучается в несколько этапов с VI по IX класс включительно. При каждом проходе учащиеся возвращаются к процентам на новом уровне, их знания пополняются, добавляются новые типы задач и приемы решений. Такое многократное обращение к понятию приводит к тому, что постепенно оно усваивается прочно и осознанно. Появляется возможность включать задачи, которые сейчас в действующих учебниках не могут рассматриваться просто в силу возрастных особенностей школьников.
Вопросы, связанные с процентами, позволяют сделать курс ориентированным на практику, показать учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес в значительной степени поддерживается также и содержанием задач, фабулы которых приближены к современной тематике и к жизненному опыту детей, а затем и подростков. Это служит достаточно сильным мотивом для решения предлагаемых задач.
Введение процентов опирается на предметно-практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.
Как и во всех основных разделах курса при изложении этой темы реализованы широкие возможности для дифференцированного обучения учащихся. Задачи предлагаются в широком диапазоне сложности – от базовых, до достаточно трудных. Учитель может подобрать материал, соответствующий возможностям каждого школьника.
При обучении решению задач на проценты учащиеся знакомятся с разными способами решения задач, причем множество приемов шире, чем это бывает обычно. Ученик овладевает разнообразными способами рассуждения, обогащая свой арсенал приемов и методов. Но при этом также важно, что он имеет возможность выбора и может пользоваться тем приемом, который ему кажется более удобным.
Глава
II. МЕТОДИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ ПРОЦЕНТОВ ПО УЧЕБНОМУ КОМПЛЕКТУ ПОД РЕДАКЦИЕЙ Г.В. ДОРОФЕЕВА.
§ 1. Методические рекомендации изложения темы «Проценты »
по учебному комплекту под редакцией Г.В. Дорофеева для V – IX классов.
Впервые о процентах учащиеся узнают в VI классе. Проценты предлагается рассматривать дважды: в начале учебного года, т.е. еще до изучения десятичных дробей (при повторении и систематизации материала, связанного с обыкновенными дробями), а затем в середине учебного года после изучения десятичных дробей. «Что такое процент» - это первая тема, изучаемая линией. На данном этапе нужно сформировать понимание процента как специального способа выражения доли величины, выработать умение выражать процент соответствующей обыкновенной дробью. Процент определяется как одна сотая часть некоторой величины. Причем перед введением определения следует рассмотреть примеры употребления процентов.
Не стоит торопиться приступать к решению задач на нахождение процента от некоторой величины. Нужно дать учащимся возможность привыкнуть к введенному понятию, освоить фактически другую терминологию. Через систему упражнений учебника ребята учатся употреблению нового термина, «переводу» задач с языка долей и дробей на язык процентов и обратно. В результате еще до решения основных задач на проценты, учащиеся прочно овладевают достаточно большим набором фактов, которые помогают им в дальнейшем. Так, они усваивают некоторые «эквиваленты»: 25% величины - это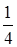 данной величины; половина некоторой величины – это 50%; 30% величины втрое больше, чем 10% и т.п. данной величины; половина некоторой величины – это 50%; 30% величины втрое больше, чем 10% и т.п.
Ребята учатся сравнивать доли величины, заданные разными способами:
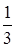 больше, чем 25%; больше, чем 25%;
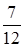 некоторой величины больше 50% этой величины; некоторой величины больше 50% этой величины;
23% меньше четверти; вся величина – это 100% и т.д.
Предлагаются упражнения, направленные на осознанное усвоение материала.
№ 99
. [15] Для каждой фразы из левого столбца подберите соответствующую фразу в правом:
1. 100% учащихся школы а) половина всех учащихся школы
2. 25% учащихся школы б) все учащиеся школы
3. 10% учащихся школы в) четверть всех учащихся
4. 50% учащихся школы г) десятая часть всех учащихся.
№ 100
. [15] Папа получил премию, 40% которой он потратил на подарок маме, 60% – на подарки детям. Все ли деньги потратил папа?
С самого начала освоения понятия учащимся рекомендуется давать больше заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Такого типа упражнения не встречаются в вышерассмотренных учебниках.
 № 98. [15]
Какая часть прямоугольника заштрихована (см. рис. 2)? Выразите эту часть в процентах. № 98. [15]
Какая часть прямоугольника заштрихована (см. рис. 2)? Выразите эту часть в процентах.
Рис. 2
Учащихся также нужно познакомить с формой неявного использования процентов, типичной для средств массовой информации.
№ 128. [15]
Объясните, используя слово «процент», что означают следующие утверждения:
а) 10 москвичей из каждых 100 нуждаются в улучшении жилья;
б) 43 человека из каждых 100 доверяют гороскопам и постоянно читают их;
в) из каждых 100 новорожденных 52 – мальчики;
г) из каждых 100 жителей Брянска 25 имеют домашних животных.
Теперь, когда учащиеся достаточно свободно и осознанно владеют понятием процента, можно перейти к задаче на нахождение процентов некоторой величины. Методически целесообразно сначала находить один процент, а потом несколько процентов этой величины.
Что касается второго приема решения (путем умножения на обыкновенную дробь), то здесь он, конечно, рассматривается, но его обязательное усвоение следует отнести на более поздние сроки.
Для успешного усвоения материала можно предложить учащимся формулировки некоторых задач в развернутом виде, т.е. к рассматриваемому в условии сюжету поставлены не один, а несколько вопросов. Так привлекается их внимание к тому, какую информацию можно извлечь из ситуации с процентами.
№ 122
. [15] В кассе профкома было 900 руб. На оплату проездных билетов израсходовали 80% этой суммы. Какие вопросы можно поставить к задаче? Ответьте на них.
№ 124. [15]
Средняя зарплата в России в середине 1993 г. составляла 120000 р. К концу года она увеличилась на 50%.
1) На сколько рублей увеличилась средняя зарплата?
2) Какой стала зарплата к концу года?
Специальная серия задач посвящена трудному вопросу об увеличении на 200%, 300% и т.д. Так учащиеся постепенно подходят к пониманию того, что, например, увеличение на 100% - это то же самое, что увеличение в 2 раза и т.д.
№ 139.
[15] В первом квартале 1995 г. квартплата в Москве в домах с лифтом была на 100% выше квартплаты в домах без лифта. Во сколько раз квартплата в домах с лифтом была выше квартплаты в домах без лифта?
К задаче приведен рисунок для того, чтобы ход решения был более понятным (см. рис. 3).
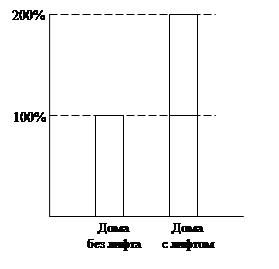
Рис. 3
В рамках этой темы учащиеся уже знакомятся с решением задачи вида К1,
задачи на увеличение (уменьшение) величины на несколько процентов предлагаются в качестве производных задачи К1
.
Второй этап в изучении процентов связывается с десятичными дробями. После изучения десятичных дробей и операций над ними нужно снова возвратится к понятию процента. Здесь предлагается два специальных пункта. В пункте «Главная задача на проценты» школьники учатся находить процент величины умножением на десятичную дробь. Прежде чем приступить к решению задач, нужно рассмотреть с учащимися правило и упражнения на перевод процентов в десятичную дробь.
«Чтобы выразить проценты десятичной дробью, нужно число, стоящее перед знаком %, разделить на 100 или, что то же самое, умножить на 0,01»
№ 596
.[15] Выразить десятичной дробью:
а) 2,5%, 18,3%, 1,6%, 54,5%;
б) 0,1%, 0,5%, 0,3%, 0,7%;
в) 120%, 137%, 240%, 350%.
Предлагается рассмотреть разные способы решения той или иной задачи.
Пример 2.
[15] Мужская рубашка стоила 8200 р. Сколько она стала стоить, когда ее цена увеличилась на 35%?
Так как 35% – это 0,35, то надо найти 0,35 от 8200 р.:
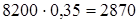 (р.) (на столько повысилась цена). (р.) (на столько повысилась цена).
Теперь найдем новую цену:
8200+2870=11070 (р.).
Можно рассуждать иначе. Старая цена составляет 100%, а новая – на 35% больше, т.е. она составляет 135%. Так как 135% – это 135:100=1,35, то цена увеличилась в 1,35 раза.
Имеем:  (р.). (р.).
Также учащиеся знакомятся с задачами типа К2.
Но авторы рассматривают эти задачи в рамках упражнений группы Б (более сложных).
№ 606. [15]
В первый час работы продавец продал 40 кг яблок. Это составило 16% от первоначального количества яблок. Сколько килограммов яблок было у продавца первоначально?
В пункте «Выражение долей в процентах» центральной является задача об определении того, сколько процентов одна величина составляет от другой.
619. В избирательном округе 2500 избирателей. В голосовании приняли участие 1300 избирателей. Какой процент избирателей участвовал в голосовании?
Здесь принят подход, в соответствии с которым сначала находят, какую часть одна величина составляет от другой, выражают ее при необходимости десятичной дробью, а затем – в процентах.
Не следует торопиться приступать к решению новых задач. В учебнике предлагается система упражнений, в которых предлагается выразить дробь (обыкновенную или десятичную) в процентах.
№ 615. [15]
Прочитайте предложение, выразив дробь в процентах:
а) бензином заполнили  бака; бака;
б) 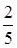 учащихся школы едут в школу на автобусе; учащихся школы едут в школу на автобусе;
в) масса сушеной вишни составляет 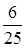 массы свежей вишни; массы свежей вишни;
г) магазин продал 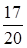 привезенного сахара. привезенного сахара.
Одна из особенностей вычислительной линии курса состоит в формировании умений выполнять прикидку или оценку результата вычислений. При изучении процентов эта работа, естественно, продолжается. Учащимся предлагаются задачи из повседневной практики, в которых требуется найти приближенно с помощью прикидки процент от заданной величины. Для этого достаточно заменить данные другими числами, близкими к ним и удобными для расчетов. Так, если требуется прикинуть, чему равно 19% от какой-либо величины, то находят 20% этой величины, т.е. ее пятую часть.
№ 595. [15]
Перед Новым годом магазин снизил цены на товары на 25%. На сколько примерно рублей понизилась цена товара, если до снижения она составляла 799 руб.? 1980 руб.? 11890 руб.?
№ 629. [15]
Часть фигуры заштрихована (см. рис 4.). Определите, какой примерно процент фигуры заштрихован, выбрав наиболее подходящий ответ из данных.
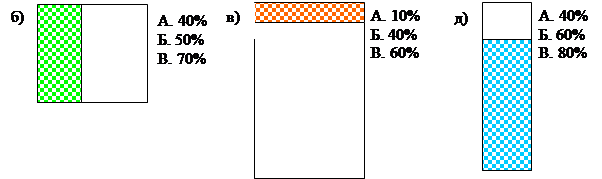
Рис. 4
Третий этап в изучении процентов отнесен к 7классу. В силу возрастных возможностей семиклассников и уже накопленного ими опыта работы с процентами учащимся становятся доступными многие вопросы из тех, что традиционно не рассматривались со всем классом, а изучались лишь в качестве дополнительных в работе с сильными учениками. Учащиеся уже знакомы со всеми основными видами задач, теперь они осваивают другие способы их решения, которые были им неизвестны.
В первой главе учебника выделен пункт «Решение задач на проценты», в котором помещен материал, позволяющий вспомнить сведения из шестого класса и продвинуться в решении задач. Теперь есть возможность рассмотреть более сложные в техническом отношении задачи. Они требуют достаточно прочного навыка представления процентов дробью и наоборот, умение находить процент от величины, понимание того, какая из величин, участвующих в задаче, принимается за 100%. Поэтому в начале теоретической части пункта рассматриваются приемы, с помощью которых десятичная дробь выражается в процентах и наоборот; здесь специально выделяется вопрос о «маленьких» (меньше 1%) и «больших» (больше 100%) процентах, как наиболее трудный для усвоения.
№ 99. [18]
В состав одного из поливитаминов входят минералы в следующих количествах: кальций и фосфор – по 4%, магний – 1,6%, железо – 0,07%, цинк – 0,06%. Сколько миллиграммов каждого минерала содержится в одной таблетке поливитамина, масса которой 25 г?
№ 88.
[18] В конце 1996 г. рабочим была выплачена премия в 250% ежемесячной зарплаты. Какую премию получил рабочий, зарплата которого была 550 тыс. р.?
Предлагаемые в системе упражнений задачи, как правило, допускают разные способы рассуждений, и учащиеся самостоятельно выбирают более удобный и понятный для себя.
Кроме задач на нахождение процента от величины, рассматриваются задачи на нахождение величины по известному ее проценту.
№ 107.
[18] После повышения цены на 30% книга стала стоить 52 рубля. Сколько стоила книга до повышения цены?
Решение. Первоначальная цена книги составляет 100%. Поэтому 52 руб., т.е. цена после подорожания, составляет 100%+30%=130% от первоначальной цены. Теперь можно решить задачу на нахождение величины по известному ее проценту.
Рассуждать можно по-разному:
1)
1% – это 52: 130=0,4(руб.), а 100% – это 0,4* 100=40(руб.);
2)
10% – 52:13=4(руб.), 100% – это 4*10=40(руб.);
3)
130% – это 1,3, поэтому 52 руб. составляют 1,3 первоначальной цены, а поэтому первоначальная цена равна 52:1,3=40(руб.).
Следует отметить еще один методический подход, использованный в изучении процентов. Первую главу заключает раздел «Для тех, кому интересно», в котором учащиеся еще раз встречаются с задачами на проценты. Здесь рассматривается восемь, если можно так выразиться, «классических олимпиадных» задач. Обычно они не включаются в учебники, т.к. являются трудными. Приведено более простое решение такого класса задач. Следует уделить им внимание хотя бы на кружке.
Задача.
[18] Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги? Вся методика обучения решению задач, принятая в учебнике, позволяет показать учащимся наглядный способ их решений с помощью рисунков (см. рис. 5). Хотя, конечно, эти задачи можно решать и арифметически.
Решение:
Цена альбома – 100%. Изобразим ее каким–либо отрезком
Увеличим этот отрезок на 25% т.е. на  его части; получим отрезок, соответствующий цене книги. его части; получим отрезок, соответствующий цене книги.
Теперь цена книги составляет 100%. Она изображена большим отрезком. Цена альбома меньше цены книги на 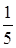 этого отрезка. Так как этого отрезка. Так как 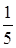 составляет 20%, то альбом дешевле книги на 20%. составляет 20%, то альбом дешевле книги на 20%.
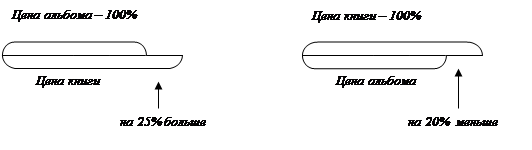
Рис. 5
При изучении следующей главы «Отношения и пропорции» учащиеся активно пользуются опытом работы с процентами и приобретают новый. В систему упражнений нужно включить новые задачные ситуации.
№ 191.[18]
В сплав входят медь, олово, сурьма в отношении 4:15:6. Сколько процентов сплава составляет каждый металл? («Деление в данном отношении»)
№ 252. [18]
За определенное время с помощью принтера было распечатано 30 страниц. Сколько страниц распечатает принтер, производительность которого на 50% больше? («Прямая и обратная пропорциональность»)
№ 269. [18]
Автомобиль за 2,4 ч проехал 60% всего пути. Через сколько минут ему останется проехать четверть всего расстояния, если он будет двигаться с той же скорость? («Решение задач с помощью пропорций»)
По мере овладения новым математическим аппаратом при изучении алгебры, учащиеся осваивают новый прием решения расчетных задач на проценты – с помощью составления уравнения.
№ 501. [18]
Вкладчик открыл в банке счет. Через год на его счету было 360000 руб., что составило 120% от суммы, которую он внес первоначально. Сколько рублей внес вкладчик при открытии счета?
В VIII классе в теме «Алгебраические дроби» учащиеся снова обращаются к задачам на проценты. Задачи на «концентрацию», «сплавы», «банковские расчеты» – это хорошие примеры практических задач, позволяющих продемонстрировать, как формальные алгебраические знания применяются в реальных жизненных ситуациях. Для того чтобы помочь учащимся осознать на новом уровне подход к решению задач с процентами, стоит обратить их внимание на то, что в учебнике приводятся образцы решения ряда задач. К разобранному образцу учащиеся при желании может вернуться вновь и использовать его в качестве опоры при решении подобной задачи.
№ 187. [17]
Разберите, как по условию задачи составлено уравнение и решите задачу. Клиент открыл счет в банке на некоторую сумму денег. Годовой доход по этому вкладу составляет 11%. Если бы он добавил 800 руб., то через год получил бы доход 220 руб. Какая сумма была внесена им в банк?
Решение. Пусть х руб. – сумма, которую клиент внес в банк. Тогда (х+800) руб. было бы на вкладе, если бы клиент добавил 800 руб.;
0,11(х+800) руб. – доход в 11%, который мог бы получить клиент с этой суммы.
Так как доход равен 220 руб., то имеем равенство:
0,11(х+800)=220.
№ 205
. [17] Два слитка, один из которых содержит 35% серебра, а другой 65%, сплавляют и получают слиток массой 20 г., содержащий 47% серебра. Какова масса каждого из этих слитков?
При изучении темы «Системы уравнений» школьникам важно показать новый метод решения задач на проценты. Учащимся предлагается план решения.
№ 656. [17]
В колбу налили некоторое количество 60%-го раствора соли и некоторое количество 80%-го раствора этой же соли. Получили 35 мл раствора, содержащего 72% соли. Сколько миллилитров каждого раствора налили в колбу?
Решите задачу, используя следующий план:
1. Обозначьте буквами количество 60%-го и 80%-го растворов соли.
2. Запишите уравнение, связывающее эти две величины и общее количество раствора.
3. Определите количество соли в получившемся растворе.
4. Запишите уравнение, связывающее количество соли в 60%-ном, 80%-ном и получившихся растворах.
5. Составьте систему и решите ее.
В IX классе в главе «Дробные уравнения» также можно предложить задачи на проценты, решение которых основано на составлении дробных рациональных уравнений.
№ 419. [16]
На первые и вторые премии в конкурсе студенческих дипломных работ было выделено 15 тыс. р., причем 40% этих денег пошло на первые премии. Вторых было выдано на 4 больше, чем первых. Сколько студентов получили первые премии и сколько вторые, если известно, что вторая премия составляла 50% первой?
Завершается линия процентных вычислений в IX классе темой «Простые и сложные проценты», включенной в изучение главы «Арифметическая и геометрическая прогрессии». Сведения о простых и сложных процентах, которые сами по себе имеют большую практическую значимость, являются достаточно благоприятным материалом для применения знаний, полученных на уроках математики. Возможность опереться на сформированные навыки в работе с процентами, на умение воспользоваться калькулятором, табличным и графическим представлением информации позволило расширить диапазон решаемых задач на проценты.
В учебнике не вводятся формулы простых и сложных процентов. Учащиеся должны решать задачи, опираясь не на формулы, а на понимание на смысл понятия «процент», на умение находить процент от числа. В теме широко используется калькулятор, который позволяет рассматривать самые разнообразные задачи.
№ 639. [16]
Один из акционеров предприятия имеет 100 акций, номинальная стоимость каждой из которых 50 р. Ежегодно ему выплачивается с каждой акции доход в 40% от ее номинальной стоимости.
а) Какой доход получит акционер за 1 год; за 2 года; за 10 лет; за n лет?
б) Через сколько лет его общий доход превзойдет удвоенную стоимость акций?
Авторы предлагают также задачи аналитического характера.
№ 654. [16]
Виктор вложил на десять лет по 1000 р. на два разных счета – с 10% годовых и 20% годовых.
а) Каким будет доход по каждому из этих счетов через год? Во сколько раз доход по второму вкладу будет больше дохода по первому вкладу?
б) Каким будет доход по каждому из этих счетов за четвертый год? Во сколько раз доход по второму вкладу больше, чем по первому?
Как вы думаете, будет ли отношение ежегодных доходов по этим вкладам увеличиваться с течением времени и почему?
В ходе решения предлагаемых авторами задач учащиеся видят, что понятия арифметической и геометрической прогрессии, а также формулы их сумм – это не просто абстрактное отвлеченное понятие, а конкретное математическое знание, необходимое для жизни.
В данном курсе в русле новой содержательной линии «Анализ данных» формулируются приемы сбора, представления и анализа информации, так или иначе связанной с процентами.
Проценты также используются в VI – VII классах для представления информации в виде таблиц и диаграмм, а VIII – IX классах – при изучении вероятно-статистического материала.
№ 155.
[15] На диаграмме показано, какой процент составляет тот или иной вид изделий от всей продукции ателье по пошиву мужской одежды.
а) Какова основная продукция данного ателье?
б) Какого цвета пиджаки ателье производит меньше всего? больше всего?
в) Сколько процентов продукции приходится на пиджаки светлого цвета? темного цвета?
г) Какой из следующих ответов может показывать , сколько процентов всех изделий составляют жилеты: 24%, 17%, 10%, 6%? (см.рис. 6)
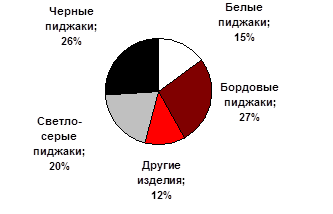
Рис. 6
№ 675.
[16] Закинул старик в реку невод. Пришел невод с таким уловом (в порядке вытаскивания):
П, О, Л, С, Я, П, К, О, З, К, П, К, Я, С, О, П, П, Л, О, О, Л, С, О, П, Л, П, К, Л, К, П, П, С, П, З, К, Я, П, З, С, О,О, Я, П, П, О, Л, С, Л, С, П,О, П, Л, К, С, О, Я, Л, П, С, О, Л, П, О, К, Л, П, О, О, П, О, Я, Л, П, С, П, О, Л, П, З.
Буквами обозначены: З – Золотая рыбка; К – Карась; Л – Лещ; О – Окунь; П – Пескарь; С – Сом; Я – Язь.
а) Произведите ранжирование ряда данных в алфавитном порядке.
б) Составьте таблицу относительных частот.
в) Какой процент пойманной рыбы составляют золотые рыбки?
г) Используя полученную стариком выборку, оцените, какие виды рыб наиболее и наименее распространены в местах, где старик закинул невод.
Таким образом, авторы данного курса уделяют большое внимание понятию процента. С помощью богатого задачного материала учащиеся могут увидеть все разнообразие применения данного математического термина.
Можно заметить, что понятие процента, как математически тривиального, вводится уже в младших классах среднего звена. В силу их возрастных особенностей и невысокой математической грамотности учащиеся не могут ознакомиться со всем спектром задач на проценты. В VII – IX классах данный термин забывается, и простейшие задачи шестого класса становятся для школьников сложными. Поэтому я считаю целесообразным уделять процентам больше внимания, как это сделано в учебном комплекте под редакцией Г. В. Дорофеева.
§ 2. Методические рекомендации для проведения урока
«Простые проценты» по учебнику «Математика. Алгебра. Функции. Анализ данных» 9 кл. под редакцией Г.В. Дорофеева.
Данный урок проводится в рамках темы «Арифметическая и геометрическая прогрессии». Он имеет две основные цели: во-первых, закрепить изученные понятия, связанные с арифметической прогрессией; во- вторых, познакомить учащихся с новым путем решения задач на проценты. Следует заметить, что в рамках IX класса проценты встречались только в теме «Уравнения и системы уравнений» в содержании двух задач. Итак, рассмотрим изложение вышеназванного урока.
1. Повторение ранее изученного материала. Нужно вспомнить с учащимися:
· Определение процента (Процент от некоторой величины – одна сотая часть данной величины).
· Как выражают проценты десятичной дробью. Для этого следует спросить учащихся общее правило (Чтобы выразить проценты десятичной дробью, нужно число, стоящее перед знаком процента, разделить на 100 или умножить на 0,01) и затем закрепить его при выполнении упражнения типа №636 а), в) (упражнение выполнить устно).
· Как увеличить (уменьшить) величину а
на р
% . Вспомнить общую формулу (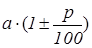 ), выписать ее на доску, выполнить упражнение на эту тему (устно) №637(Тексты задач приведены ниже). ), выписать ее на доску, выполнить упражнение на эту тему (устно) №637(Тексты задач приведены ниже).
2. Изложение нового материала. На этом этапе следует:
· объяснить учащимся, что процентные вычисления приходится выполнять в разных жизненных ситуациях, часто – это денежные расчеты;
· рассмотреть мотивационную задачу и этапы ее решения.
Задача: Пешеход перешел улицу в неположенном месте, и милиционер наложил на него штраф в 30 р. Штраф необходимо уплатить до 5 марта, после чего за каждый просроченный день будет начисляться пеня (от латинского слова poena – наказание) в размере 2% от суммы штрафа. Сколько придется заплатить пешеходу, если он просрочит уплату штрафа на 10 дней?
Для решения задачи нужно показать связь с понятием арифметической прогрессии, определить ее первый член и разность, оформить решение задачи на доске, предварительно вспомнив формулу n
-го члена арифметической прогрессии.
Пример оформления:
Величина штрафа будет расти в арифметической прогрессии, где
а1
=30; 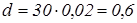 ; ; 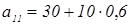 =36 р. =36 р.
Ответ: 36 р.
· Подвести итог по задаче о том, что ее решение сводится к нахождению одного из элементов арифметической прогрессии.
3. Закрепление изложенного материала. В рамках этого этапа можно предложить учащимся решить задачи № 638, №640 (для их решения вызвать учащихся к доске), №653(учащиеся решают самостоятельно, ответы выписываются на доску, при затруднении разобрать решение на доске).
4. Подвести итог по уроку. Здесь можно сказать учащимся, что в рассмотренном классе задач использовались проценты, которые авторы учебника называют простыми процентами. Решение этих задач сводится к нахождению элементов арифметической прогрессии. На следующем уроке будут рассмотрены сложные проценты, и можно ответить на вопрос, что авторы учебника назвали простыми процентами, а что – сложными.
5. Домашнее задание №639.
Задачи, предложенные к уроку
.
№ 636
Выразите десятичной дробью:
а) 25%; 38%; 60%; 80%;
в) 0,3%; 0,1%; 0,5%; 0,02%.
№ 637
Пусть цена альбома равна а рублей. Какова будет его цена, если:
а) ее повысят на 20%, на 3%, на 5,5%, на 0,7%;
б) ее снизят на 65%, на 80%, на 2%, на 0,8%?
№ 638
Ежемесячно семья Комаровых платит за электроэнергию 60 р. За каждый просроченный день взимается пеня в размере 0,5% с оплачиваемой суммы.
а) Сколько заплатят Комаровы за электроэнергию, если они просрочат оплату на 1 день; на n
дней?
б) Через сколько дней им придется заплатить за электроэнергию ее двойную стоимость?
Решение:
Плата будет расти в арифметической прогрессии, где
а1
=60 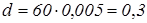
а) 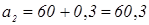
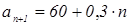
б)  n
=200
n
=200
Ответ: 200 дней.
№ 640
Цена нового автомобиля 60 000 р. При нормальных условиях эксплуатации его продажная стоимость с каждым годом уменьшается на 8% от первоначальной цены.
а) За сколько рублей сможет продать автомобиль его владелец через 5 лет эксплуатации? через n
лет эксплуатации?
б) Через сколько лет продажная стоимость автомобиля станет меньше 15000 р.? Чему будет равна эта стоимость?
Решение:
Цена автомобиля будет уменьшаться в арифметической прогрессии.
a
1
=60000
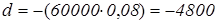
a
)
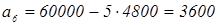
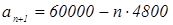
б) 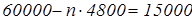
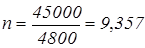 поэтому при п>9,357 цена будет меньше, значит п=10 поэтому при п>9,357 цена будет меньше, значит п=10
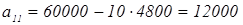
Ответ: через 10 лет его стоимость будет 12000 р.
№ 653
При покупке квартиры в строящемся доме покупатель заключил со строительной фирмой следующий договор: сразу после заключения договора он выплачивает 10% стоимости квартиры, а далее начинает ежемесячно выплачивать 1,5% от ее стоимости. Стоимость купленной им квартиры в долларах США составляет 36000.
а) Составьте формулу для вычисления суммы, выплаченной покупателем квартиры через n
месяцев после заключения договора. Вычислите, сколько было выплачено через 1 год, через 2 года после заключения договора.
б) Составьте формулу для вычисления суммы, которую осталось заплатить через n
месяцев с начала действия договора, и найдите, сколько остается заплатить через 1 год, через 2 года.
в) На сколько лет рассчитана выплата стоимости квартиры?
г) Проиллюстрируйте графически ситуации, описанные в заданиях а) и б), откладывая по горизонтальной оси число лет, в течение которых производится расчет, а по вертикальной оси – денежные суммы.
Решение:
Сначала покупатель заплатил 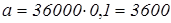 р. р.
Затем долг за квартиру можно представить виде арифметической прогрессии
а1
=36000-3600=32400 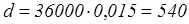
a) 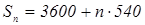
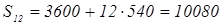
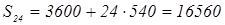
б) 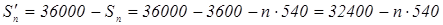
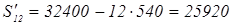
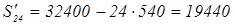
в) 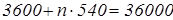
 месяцев, то есть
n
=5лет. месяцев, то есть
n
=5лет.
г) см. рис. 7
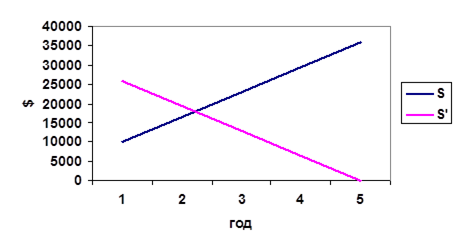
Рис. 7
№ 639
Один из акционеров предприятия имеет 100 акций, номинальная стоимость каждой из которых 50 р. Ежегодно ему выплачивается с каждой акции доход в 40% от ее номинальной стоимости.
а) Какой доход получит акционер за 1 год; за 3 года; за 10 лет; за n
лет?
б) Через сколько лет его общий доход превзойдет удвоенную стоимость акций?
Решение:
Доход по акциям растет в арифметической прогрессии.
а1
=0 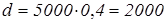
a
)
a
2
=2000
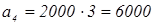
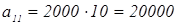
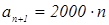
б) 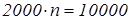
n
=5
Ответ: через 5лет.
§ 3. Методические рекомендации к проведению факультатива
«Задачи на проценты» в IX классе.
Комплект Г.В.Дорофеева не распространен в современной школе, поэтому задачи, содержащиеся в нем, можно использовать для проведения факультатива. В курсе алгебры VII – IX класса задачам на проценты не уделяется должного внимания. В то же время учащиеся владеют разнообразными способами решения текстовых задач. Данный факультативный курс поможет учащимся вспомнить понятие процента, решение основных задач на проценты, расширить кругозор учащихся, повысит интерес к математике. На факультативном курсе рекомендуется для решения некоторых задач использовать калькулятор, чтобы облегчить вычислительную работу и научится использовать калькулятор в рамках процентных вычислений.
В факультативный курс можно включить два занятия.
На первом занятии нужно вспомнить с учениками определение процента, примеры употребления процентов, историю возникновения понятия, как найти один процент (несколько процентов) от некоторой величины.
В начале занятия можно предложить учащимся боле простую задачу.
Задача 1.1.
Куртка стоит 250 р. На весенней распродаже ее можно купить на 33% дешевле. Сколько можно сэкономить, если купить куртку на распродаже?
Можно рассмотреть решение этой задачи двумя способами, в которых отражаются различные методы нахождения р
% от некоторой величины.
1 способ: сначала найти 1%, а затем 33%.
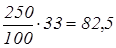
2 способ: выразить 33% десятичной дробью и найти 0,33 данной величины.
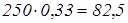
Также можно предложить учащимся задание на перевод обыкновенных и десятичных дробей в проценты, так как это часто вызывает трудности.
Задача 1.2.
Даны квадраты (см. рис. 8), ответить на вопросы.
1. Какая часть квадрата заштрихована?
2. Выразите заштрихованную часть десятичной дробью.
3. Сколько процентов квадрата заштриховано?
4. Сколько процентов квадрата не заштриховано?

рис. 8
   Далее можно предложить учащимся задачу, для решения которой нужно определить, что взять за 100%. Для более эффективного усвоения задачи можно использовать рисунок. Далее можно предложить учащимся задачу, для решения которой нужно определить, что взять за 100%. Для более эффективного усвоения задачи можно использовать рисунок.
Задача 1.3
.
В России 150 миллионов жителей. 70% всех жителей – городское население. Из них 23% – дети до 16 лет. Сколько детей до 16 лет среди городского населения?
Для решения задачи можно привести рисунок (см. рис. 9). Нужно обсудить с учащимися действия решения задачи.
1. Найти число городского населения из числа всех жителей России.
2. Из числа городских жителей найти число детей до 16 лет.

рис. 9
Рисунок (см. рис. 5) поможет школьникам решить задачу.
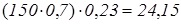
Ответ: 24,15 миллионов.
После подробного обсуждения задачи можно дать подобную задачу для самостоятельного решения.
Задача 1.4.
В библиотеке 98000 книг. Книги на русском языке составляют 78% всех книг, из них 5% – учебники. Сколько учебников на русском языке в библиотеке? (Ответ: 3822 книги).
Также в рамках занятия можно включить задачи на сравнение. Предлагая данные задачи, можно попросить учащихся высказать свои версии ответа, а затем приступить к решению.
Задача 1.5.
В магазин привезли 3 т картофеля и 900 кг помидоров. В первый день продали 30% всего картофеля и 45% всех помидор. Каких овощей продано больше и во сколько раз? (Ответ: картофеля продали больше, чем помидор в 2,2 раза).
Задача 1.6.
Сравнить числа 61% от 83 и 83% от числа 61.(Ответ: результаты равны.)
В завершении занятия учащимся можно предложить задачи на нахождение величины по известному количеству процентов.
Задача 1.7.
В коробке лежали лампочки, 4 из них разбились. Разбитые лампочки составили 2% от числа всех лампочек. Сколько всего лампочек в коробке?
Для решения задачи можно использовать алгебраический метод.
Пусть
x
лампочек в коробке. Тогда можно составить уравнение:
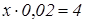 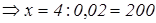
Ответ: 200 лампочек.
Затем следует сделать вывод о том, как находится величина по известному количеству его процентов, и дать задачу на закрепление.
Задача 1.8.
В школе 15 учеников учатся на «5». Это составляет 5% учащихся школы. Сколько всего учащихся в школе? (Ответ: 300 учащихся)
Домашнее задание.
Задача 1.
Дан квадрат  клеток построить фигуру площадь, которой составляет: клеток построить фигуру площадь, которой составляет:
а) 4%; б) 80%; в) 120% от площади квадрата.
Задача 2.
Из молока получается 22% сливок, из сливок получается 18% масла. Сколько масла получается из 10 кг молока?
Задача 3.
В первый час работы продавец продал 40 кг яблок. Это составило 16% от первоначального количества. Сколько килограммов яблок было у продавца первоначально?
Второе занятие следует начать с проверки домашнего задания и только после этого приступать к решению новых задач.
В начале занятия можно рассмотреть задачу об увеличении величины на несколько процентов и вспомнить метод ее решения.
Задача 2.1.
Когда цену товара увеличили на 30% ,он стал стоить 52 р. Определить первоначальную стоимость товара. (Ответ: 40 р.).
После подробного обсуждения задачи 2.1. следует предложить школьникам подобную задачу для самостоятельного решения.
Задача 2.2.
Цена товара сначала выросла на 20%, а затем снизилась на 15%, после чего товар стал стоить 102 р. Какова первоначальная стоимость товара? (Ответ: 100 р.)
После рассмотрения основных задач на проценты можно вместе с учащимися вывести общие формулы решения задач.
Общие формулы:
1.
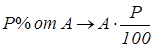
2.
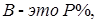 тогда 100% тогда 100% 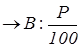
3.
А увеличить на Р% 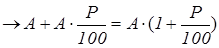
4.
А уменьшить на Р% 
где А, В – некоторые величины.
Далее можно предложить решить задачу, используя выведенные формулы. Но прежде чем приступить к решению задачи, стоит спросить учащихся о том, каков, по их мнению, будет результат.
Задача 2.3.
Цену товара увеличили на 30%, затем через некоторое время уменьшили на 30%. Сравнить первоначальную и новую цену товара, если он стоил 80 р. (Ответ: первоначальная цена больше новой.)
Как правило, еще не решая задачи, ученики делают вывод, что результаты равны. Поэтому нужно обязательно включать задачи такого плана в факультативный курс, чтобы показать «коварность» процентов.
Затем можно рассмотреть задачи на растворы и сплавы. Для того, чтобы задача была более понятна, можно привести рисунок, иллюстрирующий условие. Рисунок лучше делать, обсуждая его с учащимися.
Задача 2.4.
Сколько граммов воды надо добавить к 80 г раствора, содержащего 15% соли, чтобы получить 12% -ный раствор?

Составление таких схем поможет детям разобраться в условии и быстрее составить уравнение к задаче.
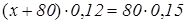
Можно предложить учащимся составить другое уравнение, сравнивая массу воды, и сделать вывод о том, какое уравнение проще.
Оставшиеся задачи школьники решают самостоятельно. На доске можно только составлять рисунок и записывать уравнение.
Задача 2.5.
Сколько граммов 25% -го сахарного сиропа нужно добавить к 200 г воды, чтобы концентрация сахара в растворе была 5%.(Эта задача аналогична задаче 2.4.)
Задача 2.6.
 Сколько граммов 30% -го раствора соли надо добавить к 80 г 12% -го раствора этой же соли, чтобы получить 20% -ный раствор. Сколько граммов 30% -го раствора соли надо добавить к 80 г 12% -го раствора этой же соли, чтобы получить 20% -ный раствор.
Задача 2.7.
Имеется лом стали двух сортов, причем первый сорт содержит 10% никеля, а второй 30%. На сколько тонн стали больше нужно взять второго сорта, чем первого, чтобы получить 200 т стали с содержанием никеля 25%?
 Для решения этой задачи лучше составить систему уравнений. Для решения этой задачи лучше составить систему уравнений.
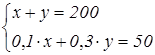
Домашнее задание.
Задача 1.
За два художественных альбома заплатили 172 р. Один альбом на 15% дороже, чем другой. Определить цену каждого альбома.
Задача 2.
Сколько граммов воды надо добавить к 180 г сиропа, концентрация сахара в котором 25%, чтобы получить сироп с концентрацией сахара 20%?
Задача 3.
Два слитка, один из которых содержит 35% серебра, а другой – 65%, сплавляют и получают слиток массой 20 г, содержащий 47% серебра. Какова масса каждого из слитков?
Задача 4.
Имеется три сосуда, в которых содержится, соответственно, 10, 30 и 5 литров растворов соляной кислоты. Процентное содержание кислоты во втором сосуде на 10% больше, чем в первом, а содержание кислоты в третьем сосуде равно 40%. Половину раствора из второго сосуда перелили в первый, а другую половину – в третий. После этого процентное содержание кислоты в первом и третьем сосудах оказалось одинаковым. Сколько процентов кислоты содержал в начале первый раствор?
§ 4. Опытное преподавание
Опытное преподавание проводилось в IX классе Богородской средней школы. Перед его проведением была изучена методическая и математическая литература, разработана методика проведения факультатива. Было проведено два занятия.
Следует отметить, что в данном классе преподавание математики ведется по учебнику под ред. С.А. Теляковского, а V – VI классе – [19], [21]. Поэтому в качестве основного источника задачного материала я взяла учебный комплект по математике под редакцией Г.В. Дорофеева.
На первом занятии было повторение понятия процента и простейших задачи типа К1
, К2
. Надо сказать, что при этом возникли некоторые трудности. Во-первых, дети не могли самостоятельно сформулировать определение процента, пришлось приводить примеры употребления данного понятия (например, в России на каждые 100 человек приходиться 12, имеющих высшее образование, это значит, что в России 12% населения имеет высшее образование) и самой его формулировать. Во-вторых, учащимся было трудно при решении задач-рисунков (например, дан квадрат, сколько процентов его площади заштриховано), поэтому использовались наводящие вопросы:
1. Какая часть квадрата заштрихована? (Этот вопрос вызвал особые трудности)
2. Выразите заштрихованную часть десятичной дробью. (Перевод обыкновенных дробей в десятичные без калькулятора осуществлялся довольно долго)
3. Сколько процентов квадрата заштриховано? (Перевод десятичных дробей в проценты дети проводили быстро)
Занятие построено таким образом, что сначала шло обсуждение решения задачи через наводящие вопросы, а затем подобную задачу дети решают самостоятельно. И, надо сказать, такая методика была довольно эффективна. Задачи для самостоятельного решения и домашнее задание ученики сделали без особых затруднений.
На втором занятии были разобраны задачи типа К3
, К4
и выведены общие формулы нахождения процентов. В ходе занятия можно было сделать вывод о том, что эти ребята владеют техникой обобщений, так как после решения частных задач общие формулы были выведены ими без труда. Дальнейшее время занятия было посвящено задачам на концентрацию. Похожие задачи ребята изучают в химии и они, как правило, вызывают трудности. Для более эффективного усвоения вводилась схема условия. Такая схема помогает определить, что лучше взять за переменную, и составить уравнение к задаче.
На этом занятии ученики могли пользоваться калькулятором. Но оказалось, что они не умеют рационально считать на калькуляторе. Поэтому нужно было объяснять рациональные приемы счета.
Большой интерес у учеников вызвала задача 2.3(Цену товара увеличили на 30%, затем через некоторое время уменьшили на 30%. Сравнить первоначальную и новую цену товара, если он стоил 80 р.). Большинство школьников считали, что первоначальная цена товара и новая цена будут равны. Некоторые считали, что цена изменится, но не могли сказать, почему. После решения данной задачи, совместными усилиями был найден ответ на вопрос о том, почему же цена изменяется.
Проверка домашнего задания показала, что материал, изученный на этих двух занятиях, был учениками усвоен.
Таким образом, я сделала вывод, что задачи на проценты нужно рассматривать хотя бы в рамках факультативного курса для сильных учащихся. Потому что практика ЕГЭ показывает, что большинство детей не справляется с задачами такого типа.
ЗАКЛЮЧЕНИЕ.
Данное исследование проводилось с целью разработки методических рекомендаций по изучению темы «Проценты» по учебникам Г.В. Дорофеева. Я считаю, что эта цель достигнута, так как мной были разработаны общие методические рекомендации к изучению темы, методические рекомендации к проведению урока и факультатива для IX класса.
Основные задачи, которые ставились перед началом исследования, были выполнены. В работе рассмотрены особенности учебного комплекта по математике Г.В Дорофеева. Проведен анализ изложения темы «Проценты» в учебниках Г.В.Дорофеева и других учебниках, рекомендованных Министерством Образования России на 2003/2004 учебный год. По разработанным методическим рекомендациям было осуществлено опытное преподавание. Также была изучена история возникновения понятия процент и систематизированы все виды задач на проценты
Гипотеза, выдвинутая в начале работы, подтвердилась. Действительно, понятие процента, как математически тривиального стоит вводить в V – VI классах, но различные типы задач на проценты следует рассматривать и в курсе алгебры VII – IX класса. Использование символической наглядности делает усвоение понятия процента и умение решать задачи на проценты более эффективным.
Таким образом, можно сделать вывод, что теме «Проценты» следует уделять больше внимания, чем это сделано в современной школе. Не во всех школах есть возможность перейти на комплект Г.В. Дорофеева, но его можно использовать в качестве учебника для факультативного курса.
С
ПИСОК ЛИТЕРАРУРЫ
1.
3000 конкурсных задач по математике. – М.: Рольф, Айрис-пресс, 1998.
2.
Арифметика: Учеб. для 5 кл. ощеобразоват. учреждений/ С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2000.
3.
Арифметика: Учеб. для 6 кл. ощеобразоват. учреждений/С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2000.
4.
Баранов О.О. Задачи на проценты как проблема нормы словоупотребления//Математика в школе. – 2003. – № 5. – с. 50 – 59.
5.
Для тех, кто работает по учебникам Г.В. Дорофеева и И.Ф. Шарыгина//Математика. – 1999. – № 15. – с. 2–8.
6.
Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б. Изучение процентов в основной школе//Математика в школе. – 2002. – №1 – с. 19 –24.
7.
Зубарева И.И. Мордкович А.Г. Математика. 5 кл.: Учеб. для общеобразоват. учреждений – М.: Мнемозина, 2003.
8.
Зубарева И.И. Мордкович А.Г. Математика. 6 кл.: Учеб. для общеобразоват. учреждений – М.: Мнемозина, 2002.
9.
Козлова Г.М. Из опыта преподавания по учебному комплекту «Математика 5»//Математика в школе. – 2002. – № 3. – с. 49 – 52.
10.
Кузнецова Л.В. и др. Методические материалы к новому учебнику для IX класса//Математика в школе. – 2000. – № 6. – с. 27–33.
11.
Кузнецова Л.В. и др. Методические материалы к новому учебнику//Математика в школе. – 1997. – № 3. – с. 34 – 39.
12.
Кузнецова Л.В. и др. Тематический и итоговый контроль в VII – IX классах по учебникам под редакцией Г.В. Дорофеева//Математика в школе. – 2002. – № 5. – с. 17–25.
13.
Кузнецова Л.В. и др. Тематический и итоговый контроль в VII – IX классах по учебникам под редакцией Г.В. Дорофеева//Математика в школе. – 2002. – № 9. – с. 33–38.
14.
Лейкина Т. Несколько замечаний по работе с учебником «Математика 7» под ред. Г.В. Дорофеева//Математика. – 1999. – № 38. – с. 23–25, 27.
15.
Математика. 6 класс: Учеб. для общеобразовательных учеб. заведений / Г.В. Дорофеев, С.Б. Суворова и др.; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – М.: Дрофа, 1998.
16.
Математика. Алгебра. Функции. 9 класс: Учеб. для общеобразовательных учеб. заведений / Г.В. Дорофеев, С.Б. Суворова и др.; под ред. Г.В. Дорофеева. – М.: Дрофа, 2000.
17.
Математика. Алгебра. Функции. Анализ данных. 8 класс: Учеб. для общеобразовательных учеб. заведений / Г.В. Дорофеев, С.Б. Суворова и др.; под ред. Г.В. Дорофеева. – М.: Дрофа, 1999.
18.
Математика. Арифметика. Алгебра. Анализ данных. 7 класс: Учеб. для общеобразовательных учеб. заведений / Г.В. Дорофеев, С.Б. Суворова и др.; под ред. Г.В. Дорофеева. – М.: Дрофа, 1997.
19.
Математика: Учеб. для 5 кл. сред. шк./ Н.Я. Виленкин, А.С. Чесноков, С.И. Шварцбурд. В.И. Жохов. – М.: Просвещение, 1992.
20.
Математика: Учеб. для 5 класса общеобразовательных учеб. заведений / Г.В. Дорофеев, С.Б. Суворова и др.; под ред. Г.В. Дорофеева, И.Ф. Шарыгина.
21.
Математика: Учеб. для 6 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2001.
22.
Нурк Э.Р., Тельгмаа А. Э. Математика. 5 кл.: Учеб. для общеобразоват. Учеб. заведений. – М.: Дрофа, 1999.
23.
Нурк Э.Р., Тельгмаа А. Э. Математика.: Учеб. для 6 кл. сред. шк. – М.: Просвещение, 1991.
24.
Первые уроки по учебному комплекту «Математика 5–8» под ред. Г.В. Дорофеева и И.Ф. Шарыгина//Математика. – 1999. – № 27. – с. 9–14.
25.
Поляков С. Зачем нужна математика тем, кому она не нужна? // Школьное обозрение. – 2002. – №4. – с. 41 – 43.
26.
Практикум по методике преподавания математики в средней школе: Учеб. пособие для студентов физ.-мат. пед. ин-тов/ Т.В. Автономова, С.Б. Верченко, В.А. Гусев и др.; Под ред. В.И.Мишина.– М.: Просвещение, 1993.
27.
Программы для общеобразовательных школ, гимназий, лицеев: Математика. 5–11 кл. / Сост. Г.М. Кузнецова, Н.Г. Миндюк. – М.: Дрофа, 2002.
28.
Самойлик Г. История математики на уроках. Проценты// Математика. – 2002 – № 36 – с. 3.
29.
Суворова С.Б., Кузнецова Л.В., Минаев С.С. Методические материалы к новому учебнику//Математика в школе. – 1998. – № 4. – с. 28 – 37.
30.
Шевкин А.В. Еще раз об изучении процентов//Математика в школе. – 1993. – №1. – с.20 – 22.
31.
Шевкин А.В. От реформы до реформы…Попытка обзора школьных учебников по математике // Школьное обозрение. – 2002. – №4. – с. 33 –40.
32.
Я познаю мир: Детская энциклопедия: Математика/ Сост. А.П. Савин, В.В. Станцо, А.Ю. Котова: Под общ. ред. О.Г. Хинн – М.: ООО «Фирма «Издательство АСТ»», 1999.
[1]
Г.В. Дорофеев – заведующий отделом математического образования Института общего и среднего образования Российской академии наук, профессор, родоначальник литературы для абитуриентов.
|