Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Южно-Уральский государственный университет»
Факультет «Приборостроительный»
Кафедра «Системы управления»
Динамический синтез системы управления
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ
по дисциплине «Теория автоматического управления»
ЮУрГУ–22020062.2010.461.ПЗ КР
Нормоконтролер, доцент Руководитель работы, доцент
________________ Г.В. Зырянов ________________ Г.В. Зырянов
«____»________________2014 г. «____»________________2014 г.
Автор работы
студент группы ПС–316
______________И.Р. Исламов
«____»________________2014 г.
Работа защищена
с оценкой
___________________________
«____»________________2014 г.
Челябинск 2014
Задание на работу
 Аннотация Аннотация
Исламов И.Р. Динамический синтез системы управления. - Челябинск: ЮУрГУ, ПС; 2010, 39 с., 23 ил., библиогр. список – 4 наим., 2 прил., 1 лист чертежа А4.
В данной работе предложен синтез системы автоматического регулирования (САР). Объект управления предполагается абстрактным.
Основной задачей курсовой работы является синтез корректирующего блока (устройства) КБ, расположенного в цепи ошибки: определение передаточной функции W
кб
(p
), обеспечивающей выполнение заданных в Задании требований к показателям точности, и к показателям качества переходного процесса в САР. При этом нужно, чтобы W
кб
(p
) была наиболее более простой для реализации, а полоса пропускания САР была, по возможности, меньше.
Кроме того, в КР проводится исследование линейной не скорректированной САР с минимально необходимым коэффициентом усиления и скорректированной САР, а также анализ влияния естественных нелинейностей (ограничение и люфт) на свойства скорректированной системы.
Оглавление
Введение...........................................................................................................................5
1 Анализ линейной САР с пропорциональным регулятором.....................................6
1.1. Получение структурной схемы линейной САР................................................6
1.2. Определение значения коэффициента передачи регулятора.............................7
1.3 Исследование устойчивости САР с пропорциональным регулятором..........8
1.4 Исследование замкнутой САР..........................................................................12
2 Динамический синтез и исследование скорректированной САР..........................17
2.1 Построение асимптотической желаемой ЛАХ...................................................17
2.2 Определение корректирующего устройства......................................................21
2.3 Определение показателей качества ПП оптимизированной САР....................22
2.4 Коэффициенты ошибок скорректированной САР.............................................33
2.5 Исследование реакций САР по ошибке..............................................................34
2.6 Область устойчивости САР……………..............................................................37
3 Анализ САР с учетом нелинейностей……………………………..........................41
3.1 Отработка ступенчатых сигналов……………………….................................41
3.2 Исследование возможных автоколебаний САР………………..........................46
Заключение.....................................................................................................................51
Библиографический список .........................................................................................52
Приложения……………………………………………………………………………53
Введение
Синтез системы автоматического управления (САУ) представляет собой расчет, имеющий конечной целью отыскание оптимальной структуры системы, и установление оптимальных величин параметров ее отдельных звеньев. При синтезе необходимо обеспечить, указанные в ТЗ требования к системе.
В настоящее время для целей синтеза широко используют вычислительные машины, позволяющие производить полное или частичное моделирование проектируемой системы. Однако моделирование на вычислительных машинах не может заменить расчетных методов проектирования, которые позволяют исследовать вопрос в общем виде и среди многих решений найти оптимальное. В данной работе для синтеза САР используется метод логарифмических амплитудных характеристик. Этот метод решения поставленной проблемы является наиболее распространенным, он достаточно хорошо изучен и прост в реализации.
Требования к качеству работы системы заданы в ТЗ как требования по точности и требования к качеству переходного процесса.
Заданные в техническом задании требования по качеству системы обеспечиваются за счет введения в систему специализированного корректирующего устройства. В результате синтеза САУ определяются расположение и тип корректирующего устройства, а также необходимые значения параметров всех элементов системы.
Далее полученная система исследуется с помощью различных тестовых сигналов и рассматривается влияние нелинейностей (насыщения в усилителе мощности и люфта кинематической обратной связи) на качество системы.
Для исследования проектируемой САР и проведения расчетов удобно пользоваться ЭВМ. В данной работе использовались следующие инженерные и математические пакеты: VisSim 7.0, MathCAD 14.
В приложениях А и В приведены структурные схемы VisSim, а также расчет формул и построение графиков в среде MathCAD.
1 Анализ линейной САР с пропорциональным регулятором
1.1 Получение структурной схемы линейной САР
Задана функциональная структура САР (рисунок 1.1):

Рисунок 1.1- Функциональная структура (схема) САР
Обозначения: 1 – задающий (или воспринимающий) блок; 2 – измеритель рассогласования; 3 – корректирующий блок КБ (пред. усилитель + корр. звено КЗ); 4 – усилитель мощности УМ; 5 – исполнительный блок ИБ (эл. двигатель пост. тока – Д); 6 – механический редуктор Р (кинематическая связь); 7 – объект управления ОУ; 8 – измерительный блок ДОС (датчик обр. связи); y – управляемая переменная (выход ОУ); y1* – задающее воздействие (напряжение, В); e – рассогласование, ошибка (напряжение, В); uk
– выход корректирующего блока (напряжение, В); uум
– выход усилителя мощности (напряжение, В); j – выход исполнительного эл. двигателя (угол, рад); j1 – угол поворота выходного вала редуктора и регулирующего органа в составе ОУ, рад; y1 – выход ДОС (напряжение, В).
Согласно техническому заданию передаточные функции отдельных звеньев линеаризованной системы имеют вид:
 (1.1) (1.1)
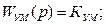 (1.2) (1.2)
 (1.3) (1.3)
 (1.4) (1.4)
 (1.5) (1.5)
 (1.6) (1.6)
Таблица 1.1 – Параметры передаточных функций линеаризованных звеньев
 |
 |
 |
 |
 |
 |
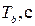 |
| 15 |
0.07 |
1 |
9 |
0.013 |
0.13 |
0.0024 |
На начальных этапах проектирования полагаем, что реализуется пропорциональный закон регулирования, т.е. 
Приведем структурную схему линейной модели САР к каноническому виду с единичной отрицательной обратной связью (ЕООС). Для этого нужно перенести блок датчика обратной связи  через точку снятия сигнала y
(t
). Полученная структурная схема изображена на рисунке 1.2. За выход системы будем принимать сигнал с выхода ДОС y
1
(t
). через точку снятия сигнала y
(t
). Полученная структурная схема изображена на рисунке 1.2. За выход системы будем принимать сигнал с выхода ДОС y
1
(t
).

Рисунок 1.2 - Структурная схема линейной модели САР с ЕООС
1.2 Определение значения коэффициента передачи регулятора
Определим минимальный коэффициент усиления разомкнутой системы  , обеспечивающий заданную точность в установившемся режиме и соответствующий ему коэффициент усиления регулятора , обеспечивающий заданную точность в установившемся режиме и соответствующий ему коэффициент усиления регулятора 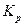 . .
Передаточная функция разомкнутой системы имеет следующий вид:
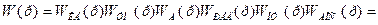  , (1.7) , (1.7)
или
 , (1.8) , (1.8)
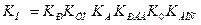 , (1.9) , (1.9)
где 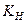 — коэффициент усиления разомкнутой (нескорректированной) системы. — коэффициент усиления разомкнутой (нескорректированной) системы.
В ТЗ заданы требования по точности, значения сведены в таблицу 1.2.
Таблица 1.2 – Требования по точности
| i
|
1 |
2 |
3 |
| Fi
|
0,15 |
0,5 |
1,6 |
| εотн
i
|
≤0,014 |
≤0,048 |
≤0,28 |
Формулу для расчета Kmin
возьмем из кратких рекомендаций по выполнению задания, метод определения Kmin
в соответствии с вариантом требований по точности:
 (1.10) (1.10)
Рассчитаем Kmin
по формуле (1.10), данные берём из таблицы 1.2, результат сведём в таблицу 1.3.
Таблица 1.3 – Результаты расчетов Kmin
| Fi
|
0,15 |
0,5 |
1,6 |
| εотн
i
|
≤0,014 |
≤0,048 |
≤0,28 |
| Ki
|
67,32 |
65,45 |
35,90 |
Таким образом Kmin
=67,32.
Коэффициент усиления регулятора, соответствующий минимальному коэффициенту усиления разомкнутой системы, можно определить как:
 (1.11) (1.11)
1.3 Исследование устойчивости САР с пропорциональным регулятором
Принимаем, что 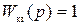 , т.е. система с пропорциональным регулятором, тогда , т.е. система с пропорциональным регулятором, тогда . .
Для применения алгебраического критерия устойчивости, сначала нужно получить характеристический полином A(p)
замкнутой САР. Для структуры с ЕООС он равен сумме числителя и знаменателя передаточной функции W(p)
разомкнутой САР.
Передаточная функция W(р)
разомкнутой по выходу ДОС линейной нескорректированной САР с пропорциональным регулятором имеет вид:

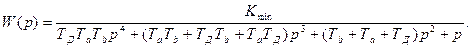 Характеристический полином замкнутой системы А(р)
будет иметь вид:
 (1.14) (1.14)
Характеристическое уравнение рассматриваемой замкнутой системы, согласно формуле (1.14), будет иметь следующий вид
 (1.15) (1.15)
Сравнивая формулу (1.14) с общим видом характеристического уравнения (1.15), можем из соответствия найти значения коэффициентов характеристического уравнения.
Таблица 1.4- Коэффициенты характеристического уравнения

|

|

|

|

|

|
1 |

|
 |

|
| 67.32 |
1 |
14.54∙10-2
|
20.332∙10-4
|
4.056∙10-6
|
Из табл. 1.4 видно, что все коэффициенты характеристического уравнения (1.14) положительны, что является необходимым условием устойчивости системы.
Согласно алгебраическому критерию Льенара-Шипара для устойчивости системы необходимо и достаточно, чтобы при положительных коэффициентах характеристического уравнения  при четном n
, все определители Гурвица нечетных порядков были больше нуля.
при четном n
, все определители Гурвица нечетных порядков были больше нуля.
В нашем случае n
=4. Вычислим определители матрицы Гурвица третьего и первого порядков:
 , (1.16) , (1.16)
 . (1.17) . (1.17)
Определители матриц Гурвица первого и третьего порядков больше нуля, следовательно, нескорректированная замкнутая САР является устойчивой.
Проверим устойчивость системы по логарифмическим амплитудной и фазовой характеристикам (ЛАХ и ЛФХ) разомкнутого контура САР с применением частотного критерия устойчивости Найквиста.
ЛАХ и ЛФХ разомкнутой системы строятся согласно следующим формулам:
 , (1.18) , (1.18)
 . (1.19) . (1.19)
Для построения располагаемой асимптотической логарифмической амплитудной характеристики найдём вспомогательные данные - частоты сопряжения и значение 20lgK:
 , , 
 , , 
 , , 

Зная ЛАХ для каждого типового звена, являющегося сомножителем передаточной функции (1.12), можно найти асимптотическую ЛАХ системы, как сумму ЛАХ типовых звеньев.
ЛАХ и ЛФХ для разомкнутой нескорректированной САР с пропорциональным регулятором с передаточной функцией (1.12) изображены на рисунке 1.3.


Рисунок 1.3 - ЛАХ и ЛФХ для разомкнутой нескорректированной САР с пропорциональным регулятором
По ЛЧХ разомкнутой системы можно оценить устойчивость замкнутой системы по критерию Найквиста. Устойчивая в разомкнутом состоянии система будет устойчива в замкнутом состоянии, если выполняется равенство:  , где , где  - число положительных переходов ФЧХ через один из критических уровней - число положительных переходов ФЧХ через один из критических уровней  в диапазоне положительности ЛАХ; в диапазоне положительности ЛАХ;  - число отрицательных переходов; - число отрицательных переходов;  - число правых полюсов. - число правых полюсов.
Согласно (1.12) разомкнутая система не имеет правых корней. Из рисунка 1.3 видно, что количество отрицательных переходов  , количество положительных переходов , количество положительных переходов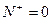 . Так как . Так как 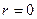 , то , то  . Следовательно, замкнутая система устойчива. . Следовательно, замкнутая система устойчива.
По графикам ЛАХ и ЛФХ (рисунок 1.3) определим частоту среза и критическую частоту.
Частота среза разомкнутой системы, найденная по графику ЛАХ (пересечение ЛАХ уровня 0дБ), равна:
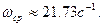
Критическая частота находится по графику ЛФХ (пересечение ЛФХ уровня -180 ): ):

По графикам ЛАХ и ЛФХ разомкнутой системы также можно определить запасы устойчивости системы по модулю и по фазе. На рисунке 1.3 отмечены запасы устойчивости по амплитуде и фазе:
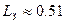 дБ; (1.20) дБ; (1.20)
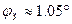 . (1.21) . (1.21)
1.4 Исследование замкнутой САР
График переходной функция h(t)
(по выходу ДОС) для замкнутой системы, полученный методом компьютерного моделирования в среде Vissim приведен на рисунке 1.4.

Рисунок 1.4 - Переходная функция h(t)
для замкнутой САР
Как видно из графика переходной функции h(t)
,  , следовательно, система устойчива. , следовательно, система устойчива.
Определим прямые показатели качества переходного процесса.
а) Перерегулирование 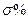 определяется согласно формуле: определяется согласно формуле:
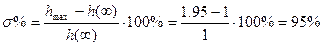 . (1.22) . (1.22)
б) Время регулирования 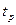 — время, за которое график переходного процесса укладывается в 5% «коридор» от установившегося значения. — время, за которое график переходного процесса укладывается в 5% «коридор» от установившегося значения.
По графику найдем  . .
Определим корневые показатели качества.
Решим характеристическое уравнение (1.15):
 (1.23) (1.23)
Решая уравнение (1.22) в среде MathCAD, получим следующие корни:
 (1.24) (1.24)
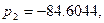 (1.25) (1.25)
 (1.26) (1.26)
 (1.27) (1.27)
Расположение характеристических корней  на комплексной плоскости изображено на рисунке 1.5. на комплексной плоскости изображено на рисунке 1.5.
 
Рисунок 1.5 - Расположение характеристических корней  на комплексной плоскости на комплексной плоскости
Определим корневые показатели качества:
а) степень устойчивости h определим по формуле:
η
=min|Re p
k
|=0.149135 (1.28)
б) коэффициент колебательности m определим по формуле:
μ
=max(Im pk
/Re pk
)=145.54 (1.29)
Определим частотные показатели качества.
АЧХ и ВЧХ замкнутой системы приведены на рисунках 1.6 и 1.7.

Рисунок 1.6 – АЧХ замкнутой системы

Рисунок 1.7 – ВЧХ замкнутой системы
Показатель колебательности М:
 (1.30) (1.30)
Частота амплитудного резонанса: 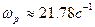 . (1.31) . (1.31)
Граница полосы пропускания:  . (1.32) . (1.32)
Максимальное и минимальное значение ВЧХ:
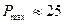 , ,  , , 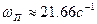 . .
Полученные в результате исследования частотные показатели качества сведены в таблицу 1.5.
Таблица 1.5 – Частотные показатели качества
 , дБ , дБ |
 , ° , ° |
 , с-1 , с-1
|
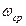 , с-1 , с-1
|
 , с-1 , с-1
|
M
|
| 0.51 |
1.05 |
21.78 |
21.73 |
31.1 |
9.39 |
Для данной исследуемой системы с пропорциональным регулятором были получены  дБ и дБ и  . Эти значения запасов устойчивости меньше типовых значений . Эти значения запасов устойчивости меньше типовых значений  дБ, дБ,  . .
Выводы
В данном разделе была исследована система с пропорциональным законом регулирования. Система получилась устойчивой при заданных требованиях по точности, но данная система не обеспечивает требований по качеству ПП, заданному в техническом задании. Целесообразно ввести в систему специализированное корректирующее звено, которое позволит обеспечить выполнение необходимых требований к качеству переходного процесса.
2 Динамический синтез и исследование скорректированной САР
2.1 Построение желаемой ЛАХ
Система с пропорциональным регулятором не может обеспечить заданного качества управления. Улучшить свойства системы можно с помощью введения в нее корректирующего устройства КУ включаемого последовательно в разомкнутую цепь системы и обеспечивающего выполнение следующих условий:
1) все требования по качеству САР, указанные в техническом задании,
2) минимизация частоты среза замкнутой системы,
3) простота структуры синтезируемого КУ.
Синтез систем автоматического регулирования методом логарифмических амплитудных характеристик является в настоящее время одним из самых удобных и наглядных, данная методика синтеза основывается на использовании частотных критериев качества. Синтез проводится следующим образом. Строится желаемая ЛАХ, исходя из требований ТЗ.
Эта желаемая характеристика сравнивается с той, которую данная система имеет без коррекции. Определяется передаточная функция корректирующего устройства так чтобы, при его включении в систему, в последней получалась желаемая форма ЛАХ. Затем оценивается получающаяся при этом величина запаса устойчивости системы и другие качественные показатели.
Основные этапы метода желаемой ЛАХ:
1. Построение располагаемой ЛАХ разомкнутой системы  . .
2. Построение желаемой ЛАХ разомкнутой системы  на основе требований, предъявляемым к проектируемой системе. на основе требований, предъявляемым к проектируемой системе.
3. Определение передаточной функции КЗ 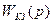 и соответствующих и соответствующих  и и  . .
Построение желаемой ЛАХ ведется отдельно для каждого участка ЛАХ: для низких, средних и высоких частот. Низкочастотный диапазон определяет точность работы системы в установившемся режиме, среднечастотный диапазон определяет качество переходных процессов, высокочастотный диапазон влияет на помехоустойчивость системы.
Построим низкочастотную часть желаемой ЛАХ. Для обеспечения заданных требований по точности в установившемся режиме низкочастотный участок ЛАХ должен проходить выше так называемой запретной области.
Требования по точности, представленные в техническом задании:
 . .
F1
=0.15 Гц; F2
=0.5 Гц: F3
=1.6 Гц.
Вычислим координаты контрольных точек, определяющей границу запретной области по точности, в которую не должна заходить ЛАХ желаемой системы по формулам:
 . (2.1) . (2.1)
 . (2.2) . (2.2)
L1
=37.08 дБ.
L2
=26.38 дБ.
L3
=11.06 дБ.



Полученная запретная область  показана на рисунке 2.1. показана на рисунке 2.1.
С целью упрощения процедуры динамического синтеза асимптотическую желаемую ЛАХ выбираем симметричной с типовыми наклонами асимптот (-20-40-20-40-60…)
Так как желаемая ЛАХ не должна заходить в запретную область, а при частоте сопряжения w1
реальная желаемая ЛАХ пройдет ниже точки сопряжения (на частоте wa
) на 3дБ, то желаемая ЛАХ должна быть поднята вверх на 3дБ, что соответствует увеличению коэффициента усиления разомкнутой системы в 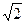 раз: раз:
 , (2.3) , (2.3)
 дБ. (2.4) дБ. (2.4)
Определим частоту сопряжения  , для этого через третью контрольную точку проведем асимптоту с наклоном -40 дБ/дек. При пересечении этой асимптоты с асимптотой с наклоном -20 дБ/дек получим первую частоту сопряжения , для этого через третью контрольную точку проведем асимптоту с наклоном -40 дБ/дек. При пересечении этой асимптоты с асимптотой с наклоном -20 дБ/дек получим первую частоту сопряжения  =3.63с-1
. =3.63с-1
.
Определим постоянную времени  , соответствующей частоте , соответствующей частоте  : :
 с, (2.5) с, (2.5)
Определим базовую частоту  : :  . (2.6) . (2.6)
 . (2.7) . (2.7)
Найдем частоту среза 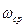 желаемой ЛАХ из формулы: желаемой ЛАХ из формулы:
 , (2.8) , (2.8)
 . (2.9) . (2.9)
Определим вторую постоянную времени и соответствующую ей частоту:
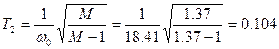 с, (2.10) с, (2.10)
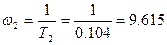 с-1
. (2.11) с-1
. (2.11)
 . (2.12) . (2.12)
Начиная с частоты 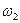 желаемая ЛАХ имеет наклон -20 дБ/дек, характерный для среднечастотного участка «симметричной» типовой желаемой ЛАХ. желаемая ЛАХ имеет наклон -20 дБ/дек, характерный для среднечастотного участка «симметричной» типовой желаемой ЛАХ.
При построении высокочастотного участка желаемой ЛАХ по методике Бесекерского необходимо помимо требования близости желаемой и располагаемой ЛАХ, рассмотреть еще одно требование. Это требование позволяет обеспечить нужный запас по фазе в среднечастотном диапазоне:
 , (2.13) , (2.13)
где М=1.37 , возьмем из ТЗ.
Для упрощения передаточной функции КЗ выберем постоянные времени 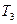 и и  следующим образом: следующим образом:
 с, (2.14) с, (2.14)
 с. (2.15) с. (2.15)
Частоты сопряжения, найденные как обратные величины постоянных времени:
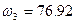 с-1
, (2.16) с-1
, (2.16)
 , (2.17) , (2.17)
 с-1
, (2.18) с-1
, (2.18)
 . (2.19) . (2.19)
По формуле (2.13) определим постоянную времени  : :
 c. (2.20) c. (2.20)
Значение  подбиралось так, чтобы M максимально приближалось к требованию по качеству переходного процесса, а также для улучшения помехоустойчивости на высокочастотном участке ЛАХ. В результате выбрано значение подбиралось так, чтобы M максимально приближалось к требованию по качеству переходного процесса, а также для улучшения помехоустойчивости на высокочастотном участке ЛАХ. В результате выбрано значение  с. с.
Соответствующая  частота сопряжения: частота сопряжения:
 с-1
, (2.21) с-1
, (2.21)
 , (2.22) , (2.22)
Последовательно уменьшая наклон на -20 дБ/дек при переходе через очередную частоту сопряжения, получим высокочастотный участок желаемой ЛАХ.
Полученная желаемая ЛАХ  приведена на рисунке 2.1. приведена на рисунке 2.1.
Передаточная функция разомкнутой скорректированной системы, полученная по скорректированной желаемой ЛАХ имеет следующий вид:
 , (2.23) , (2.23)
 . (2.24) . (2.24)
Запретная область для ЛФХ строится по формулам:
 , (2.25) , (2.25)
 , (2.26) , (2.26)
 . (2.27) . (2.27)
Определим дополнительные величины для построения запретной области по ЛФХ:
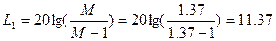 дБ, (2.28) дБ, (2.28)
 дБ. (2.29) дБ. (2.29)
Значение показателя колебательности скорректированной системы оказалось меньше заданного:  при заданном ограничении при заданном ограничении 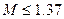 . График АЧХ замкнутой системы, по которому определялось значение М
, приведен на рисунке 2.2. . График АЧХ замкнутой системы, по которому определялось значение М
, приведен на рисунке 2.2.
ЛАХ и ЛФХ располагаемой и скорректированной систем изображены на рисунке 2.1. Из рисунка можно сделать следующий вывод: так как ЛФХ скорректированной системы не заходит в запретную зону, а ЛАХ лишь касается ее на частоте сопряжения  с-1
, то требования по качеству удовлетворяются с минимальным запасом, что как раз удовлетворяет инженерным рекомендациям по построению оптимизированной системы. с-1
, то требования по качеству удовлетворяются с минимальным запасом, что как раз удовлетворяет инженерным рекомендациям по построению оптимизированной системы.
 Рисунок 2.2 – АЧХ замкнутой скорректированной системы Рисунок 2.2 – АЧХ замкнутой скорректированной системы
2.2 Определение корректирующего устройства
Асимптотическая ЛАХ и ЛФХ корректирующего устройства для желаемой системы приведены на рисунке 2.1. Асимптотическая ЛАХ КЗ может быть построена графически вычитанием ЛАХ располагаемой нескорректированной системы из ЛАХ желаемой скорректированной системы. Аналогичным образом строится ЛФХ КЗ.
Перейдем теперь к определению передаточной функции КЗ. Искомая передаточная функция последовательного КЗ будет равна отношению передаточных функций разомкнутой скорректированной (2.23) и разомкнутой исходной (1.12) систем:
 , (2.30) , (2.30)
или для ЛАХ: 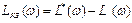 (2.31) (2.31)
2.3 Определение показателей качества ПП скорректированной САР
Передаточная функция замкнутой скорректированной системы «вход – выход ДОС»:
 ; (2.32) ; (2.32)
Передаточная функция замкнутой скорректированной системы «вход–ошибка системы» определяется согласно выражению:

Передаточная функция замкнутой скорректированной системы «вход – выход усилителя мощности» имеет вид:
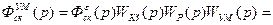 
График переходной функция h(t)
(по выходу ДОС) для замкнутой скорректированной системы, полученный методом компьютерного моделирования в среде Vissim приведен на рисунке 2.3.

Рисунок 2.3 - Переходная функция h(t)
для замкнутой скорректированной САР
Как видно из графика переходной функции h(t)
,  , следовательно, система устойчива. , следовательно, система устойчива.
Определим прямые показатели качества переходного процесса:
а) перерегулирование 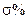 определяется согласно формуле: определяется согласно формуле:
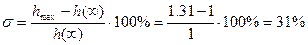 . (2.33) . (2.33)
б) время регулирования 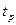 — время, за которое переходная функция укладывается в 5% «коридор» от установившегося значения — время, за которое переходная функция укладывается в 5% «коридор» от установившегося значения
По графику найдем 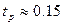 с. с.
Очевидно, что прямые показатели качества переходного процесса скорректированной САР превосходят прямые показатели качества нескорректированной системы.
Определим корневые показатели качества.
Решим характеристическое уравнение для скорректированной САР. Для этого запишем характеристический полином А(р)
замкнутой системы.
 , ,
 (2.34) (2.34)
В числовом виде:
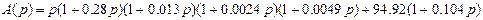 (2.35) (2.35)
Полюсами системы являются корни характеристического уравнения  . Для решения этого уравнения воспользуемся программой Mathcad. Получили следующие результаты: . Для решения этого уравнения воспользуемся программой Mathcad. Получили следующие результаты:
 , ,
 , ,
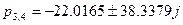 , ,
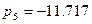 . .
Изображенные на комплексной плоскости полюса замкнутой системы приведены на рисунке 2.4.

Рисунок 2.4 – Расположение корней на комплексной плоскости
Вычислим корневые показатели качества:
1. степень устойчивости  : :
 . .
2. коэффициент колебательности  : :
 . .
Определим частотные показатели качества.
Построим ЛАХ и ЛФХ разомкнутой скорректированной системы. ЛАХ и ЛФХ разомкнутой скорректированной системы строятся согласно следующим формулам:
 , (2.36) , (2.36)
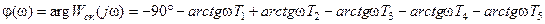 . (2.37) . (2.37)
ЛЧХ разомкнутой скорректированной системы изображены на рисунке 2.5.
  Рисунок 2.5 – ЛЧХ разомкнутой скорректированной системы Рисунок 2.5 – ЛЧХ разомкнутой скорректированной системы
По рисунку 2.5 определены значения частоты среза, запасов устойчивости по амплитуде и фазе разомкнутой скорректированной системы:
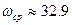 с-1
, с-1
, дБ, дБ,
 . .
Запасы устойчивости скорректированной системы значительно выше запасов устойчивости системы с пропорциональным регулятором. Кроме того, запасы устойчивости скорректированной системы находятся в диапазоне типовых значений ( дБ, дБ,  . .
По найденному значению запаса устойчивости по амплитуде оценим величину критического коэффициента усиления и коэффициента усиления регулятора:
 , (2.36) , (2.36)
 . (2.37) . (2.37)
График  представлен на рисунке 2.6 представлен на рисунке 2.6


Рисунок 2.6 АЧХ замкнутой скорректированной системы по ошибке.
По графику  определим амплитуду относительной ошибки на частотах заданных в ТЗ определим амплитуду относительной ошибки на частотах заданных в ТЗ
F1
=0.15 Гц=0.94 рад/с 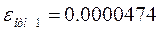
F2
=0.5 Гц=3.14 рад/с 
F3
=1.3 Гц=10.05 рад/с 
Требования ТЗ по точности выполняются.
Построим ЛЧХ замкнутой скорректированной системы («вход – выход ДОС»). Передаточная функция замкнутой скорректированной системы имеет вид (2.32). ЛАХ и ЛФХ, АЧХ замкнутой скорректированной системы строятся согласно следующим формулам:
 , (2.38) , (2.38)
 , (2.39) , (2.39)
 . (2.40) . (2.40)
Изобразим АЧХ, ЛАХ и ЛФХ замкнутой скорректированной системы на рисунках 2.7 и 2.8 соответственно.

Рисунок 2.7 – АЧХ замкнутой скорректированной системы
  Рисунок 2.8 – ЛЧХ замкнутой скорректированной системы Рисунок 2.8 – ЛЧХ замкнутой скорректированной системы
По графикам ЛАХ и ЛФХ замкнутой системы определим:
– частоту амплитудного резонанса:
 с-1
, (2.41) с-1
, (2.41)
– частоту среза замкнутой системы:
 с-1
, (2.42) с-1
, (2.42)
– полосу пропускания: с-1
, (2.43) с-1
, (2.43)
– показатель колебательности:
 . (2.44) . (2.44)
Показатель колебательности скорректированной системы удовлетворяет требованиям ТЗ
Вещественная частотная характеристика замкнутой скорректированной системы («вход – выход ДОС»), определяется выражением:
 , (2.45) , (2.45)
и представлена на рисунке 2.9.

Рисунок 2.9 – ВЧХ замкнутой скорректированной системы
По ВЧХ определяем следующие параметры:
- максимальное значение ВЧХ 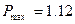 , ,
- модуль минимального значения ВЧХ 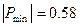 , ,
- диапазон положительности ВЧХ 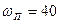 с-1
, с-1
,
- значение ВЧХ на нулевой частоте 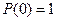 . .
Сравним полученные прямые, частотные, корневые показатели качества переходного процесса скорректированной и нескорректированной САР. Все показатели качества сведены в таблицу 2.1.
Скорректированная система имеет значительный запас устойчивости. Заметим, что хорошо демпфированная система имеет запас устойчивости по амплитуде 6…20 дБ и запас устойчивости по фазе 30…60˚. Скорректированная система этим требованиям удовлетворяет. Следовательно, можно говорить о положительных результатах синтеза КУ для проектируемой САР.
Таблица 2.1 – Сравнение показателей качества САР
| Показатели качества |
Нескорректированная САР |
Скорректированная САР |
| Прямые |
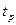 ,с ,с |
22 |
0.15 |
 |
95 |
31 |
| Корневые |
 |
145.54 |
1.741 |
 |
0.149 |
11.717 |
| Частотные |
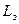 , дБ , дБ |
0.51 |
13 |
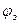 , ,  |
1.05 |
43.5 |
 |
21.78 |
31.93 |
 |
21.73 |
54.25 |
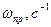 |
33.1 |
60.21 |
| М
|
9.39 |
1.36 |
| P
max
|
25 |
1.12 |
| |P
min
| |
45.1 |
0.58 |
 |
21.6 |
40 |
Передаточная функция по выходу усилителя имеет вид:
 . (2.46) . (2.46)
Найдем начальное значение переходной функции по выходу усилителя мощности 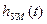 . Воспользуемся теоремой о предельных значениях: . Воспользуемся теоремой о предельных значениях:
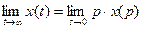 , (2.47) , (2.47)
 . (2.48) . (2.48)
С учетом того, что переходная функция  — это реакция системы на единичную ступенчатую функцию — это реакция системы на единичную ступенчатую функцию  и и  , то получим: , то получим:
 . (2.49) . (2.49)
Тогда для переходной функции  формулы (2.47) и (2.48) примут вид: формулы (2.47) и (2.48) примут вид:
 , (2.50) , (2.50)
 . (2.51) . (2.51)
Начальное значение переходной функции по выходу усилителя мощности 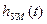 : :
 В. (2.52) В. (2.52)
Начальное значение  зависит от величины коэффициента усиления установленного ранее пропорционального регулятора, а также коэффициента усиления УМ зависит от величины коэффициента усиления установленного ранее пропорционального регулятора, а также коэффициента усиления УМ  , а также постоянных времени , а также постоянных времени  , ,  , ,  и и  . .
Переходная функция 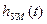 представлена на рисунке 2.10. представлена на рисунке 2.10.

Рисунок 2.10 – График переходной функции 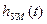
По графику 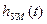 найдем начальное значение переходной функции: найдем начальное значение переходной функции:  В. (2.52) В. (2.52)
При сравнении полученного путем моделирования начального значения переходной функции 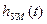 с его расчетным значением делаем вывод, что эти значения совпадают. с его расчетным значением делаем вывод, что эти значения совпадают.
Определим максимальную величину 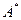 входного ступенчатого сигнала, при котором система работает в зоне линейности усилителя мощности, по формуле: входного ступенчатого сигнала, при котором система работает в зоне линейности усилителя мощности, по формуле:
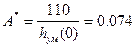 В. (2.53) В. (2.53)
Определим границу диапазона частот  , в котором УМ работает в зоне линейности при входном сигнале , в котором УМ работает в зоне линейности при входном сигнале  (в установившемся режиме). АЧХ замкнутой системы по выходу усилителя мощности определяется по формуле: (в установившемся режиме). АЧХ замкнутой системы по выходу усилителя мощности определяется по формуле:
 . (2.54) . (2.54)
График АЧХ представлен на рисунке 2.11.

Рисунок 2.11 – АЧХ замкнутой системы по выходу УМ
Из графика АЧХ получим:
 . (2.55) . (2.55)
2.4 Коэффициенты ошибок скорректированной САР
Передаточная функция замкнутой скорректированной системы «вход – выход ДОС»:
 . (2.56) . (2.56)
Передаточная функция замкнутой скорректированной системы «вход–ошибка системы» определяется согласно выражению:
 , (2.57) , (2.57)
Запишем передаточную функцию скорректированной системы по ошибке:
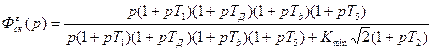 , (2.58) , (2.58)
Точность системы можно определить по коэффициентам ошибок (КО). Коэффициенты ошибок характеризуют влияние каждой производной входного сигнала на вынужденную составляющую ошибки системы.
Вычислим коэффициенты ошибок по формуле:
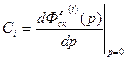 . (2.59) . (2.59)
Запишем формулы для КО  , ,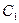 и и  : :
 , (2.60) , (2.60)
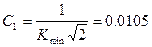 , (2.61) , (2.61)
 . (2.62) . (2.62)
Равенство нулю первого коэффициента ошибок свидетельствует о том, что исследуемая САР имеет первый порядок астатизма.
Найденные значения коэффициентов ошибок зависят от коэффициента усиления разомкнутой системы. Кроме того, коэффициенты ошибок более высокого порядка также будут зависеть от коэффициента усиления разомкнутой системы. Следует заметить, что характер зависимости – обратный. Следовательно, эффективный способ повышения точности системы – увеличение коэффициента передачи разомкнутого контура.
2.5 Реакции САР по ошибке
Рассмотрим подачу линейного сигнала на вход САР.
Входной сигнал с постоянной скоростью и его изображение по Лапласу имеют соответственно вид:
х(t) = а
×
t
, (2.63)
 (2.64) (2.64)
где а
= 11 В/с – заданное в техническом задании значение скорости.
Реакцию системы на сигнал с постоянной скоростью по выходу ошибки определим как оригинал от изображения Лапласа:
 . (2.65) . (2.65)
Вынужденную составляющую ошибки, определим по формуле:
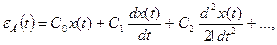 (2.66) (2.66)
где  , ,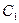 , ,  – коэффициенты ошибок, найденные выше. – коэффициенты ошибок, найденные выше.
Таким образом, получим
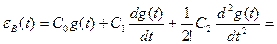 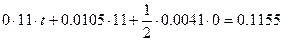 (2.67) (2.67)
График реакции САР по ошибке e
(t)
на линейный входной сигнал и график вынужденной реакции  приведены на рисунке 2.12. приведены на рисунке 2.12.

Рисунок 2.12 - Графики и и  при линейном входном сигнале при линейном входном сигнале
При воздействии на систему линейного сигнала, переходная составляющая ошибки с течением времени затухает, следовательно,  при при  . Ошибка устанавливается в постоянное значение. . Ошибка устанавливается в постоянное значение.
Рассмотрим подачу квадратичного сигнала на вход САР.
Входной сигнал с постоянным ускорением имеет соответственно вид:
х(t) = а
×
t+b∙t2
, (2.68)
где а
= 11 В/с , b
=30 B/c – заданное в техническом задании значение.
Вынужденную составляющую ошибки, определим по формуле:
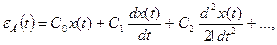 (2.69) (2.69)
где  , , 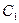 , ,  – коэффициенты ошибок, найденные выше. – коэффициенты ошибок, найденные выше.
Таким образом, получим
 
 . (2.70) . (2.70)
График реакции САР по ошибке e
(t)
на квадратичный входной сигнал и график вынужденной реакции  приведены на рисунке 2.13. приведены на рисунке 2.13.

Рисунок 2.13 - Реакция САР по ошибке e
(t)
на квадратичный
входной сигнал и график вынужденной реакции 
Из рисунка 2.13 видно, что при квадратичном входном сигнале ошибка в системе в установившемся режиме постоянно возрастает, поэтому применение данной системы при квадратичном входном воздействии невозможно.
2.6 Область устойчивости
При расчете и проектировании САУ необходимо исследовать влияние её различных параметров на устойчивость. Для решения этой задачи служит построение областей устойчивости, то есть определение таких областей значений параметров, при которых система оказывается устойчивой.
Рассмотрим постановку задачи построения области устойчивости.
Для проектируемой САР необходимо в плоскости параметров системы  построить область устойчивости. Граница этой области соответствует нахождению системы на границе устойчивости. Точки, находящиеся внутри области, соответствуют устойчивости рассматриваемой САР. построить область устойчивости. Граница этой области соответствует нахождению системы на границе устойчивости. Точки, находящиеся внутри области, соответствуют устойчивости рассматриваемой САР.
Построение областей устойчивости возможно с помощью любого из критериев устойчивости. Для построения области устойчивости воспользуемся методом D-разбиения.
Метод D-разбиения заключается в разделении n
-мерного пространства параметров на области, каждой из которых соответствует определенное число правых корней характеристического уравнения. Область, которой соответствует ноль правых корней, является областью устойчивости.
Построим область устойчивости в плоскости  и и  . .
Характеристический полином системы имеет вид:
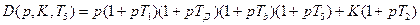 , (2.71) , (2.71)
где  . .

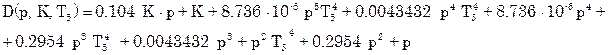
(2.72)
Определим основные формулы для построения границ области устойчивости.
Подставим в выражение (2.72)  : :
 Уравнение (2.72) будет выполнено, при условии, что действительная и мнимая части равны нулю, то есть данное уравнение можно записать через систему уравнений: Уравнение (2.72) будет выполнено, при условии, что действительная и мнимая части равны нулю, то есть данное уравнение можно записать через систему уравнений:
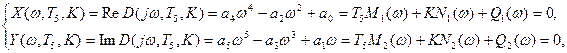 (2.73) (2.73)
где
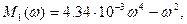
 , ,
 , ,
 , ,
 , ,
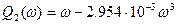 . .
Решим полученную систему уравнений методом Крамера:
 (2.74) (2.74)
 (2.75) (2.75)
 (2.76) (2.76)
 , (2.77) , (2.77)
 . (2.78) . (2.78)
В итоге мы получили параметрическое уравнение (параметр – ω
) для основной границы D
-разбиения.
Построим зависимости (2.77) и (2.78). Из рисунка 2.14 видно, что при возрастании частоты  асимптотически стремиться к нулю, а асимптотически стремиться к нулю, а  – к бесконечности. – к бесконечности.
 
Рисунок 2.14 – График зависимости 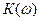 и и
Основная граница области D-разбиения отмечается 2-х кратной штриховкой. При движении по кривой D-разбиения в сторону возрастания  штриховку наносят слева, если определитель штриховку наносят слева, если определитель  положителен, и справа, если положителен, и справа, если  отрицателен. Зависимость отрицателен. Зависимость  представлена на рисунке 2.15. представлена на рисунке 2.15.

Рисунок 2.15 – Зависимость 
Нанесем штриховку согласно правилу: при перемещении по кривой в направлении возрастания частоты кривая штрихуется слева, если определитель  положителен, или справа, если определитель положителен, или справа, если определитель  отрицателен. отрицателен.
Из рисунка 2.15 видно, что якобиан  положителен (имеет знак «+») при положительных значениях частоты. Следовательно, на плоскости параметров положителен (имеет знак «+») при положительных значениях частоты. Следовательно, на плоскости параметров  - - штриховку основной границы D-разбиения нанесем слева по возрастанию частоты штриховку основной границы D-разбиения нанесем слева по возрастанию частоты  . .
Определим особые границы области D-разбиения.
Для построения особой границы необходимо в характеристическом уравнении замкнутой системы (2.72) приравнять к нулю старший и младший коэффициенты, при этом получим:
 = 0, при = 0, при 
 = 0, при = 0, при  . .
Или
 (2.79) (2.79)
Отметим в плоскости параметров  - - особые границы (2.79). Штриховка особой границы наносится со стороны асимптотического сближения основной и особой границы, то есть в данном случае сверху оси параметра особые границы (2.79). Штриховка особой границы наносится со стороны асимптотического сближения основной и особой границы, то есть в данном случае сверху оси параметра  и правее оси параметра и правее оси параметра  . .
Построим в плоскости параметров  и К основную границу D-разбиения. При построении достаточно рассмотреть изменения частоты от нуля до плюс бесконечности постольку, поскольку и К основную границу D-разбиения. При построении достаточно рассмотреть изменения частоты от нуля до плюс бесконечности постольку, поскольку и и 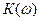 – четные функции. – четные функции.
 
Основная граница D-разбиения
Особые границы Т5
, К
+ – номинальная точка
Рисунок 2.16 – Область устойчивости САР
Область, для которой все штриховки направлены внутрь, называется претендентом. И, так как в этой области находится номинальная точка (0.0049; 94.92), в которой система является устойчивой, эта область является областью устойчивости системы.
Также по рисунку 2.16 определим критический коэффициент усиления системы при заданном Т5
: 
Если сравнить полученное значение граничного коэффициента усиления с найденным в пункте 2.3 ( ), то можно говорить, что они практически совпадают. ), то можно говорить, что они практически совпадают.
3 Анализ САР с учетом нелинейностей
В рассматриваемой системе присутствуют нелинейности, которые не учитывались на первых этапах исследования системы (производилась так называемая линеаризация на физическом уровне). В действительности же, УМ имеет ограниченную зону линейности ( ), а между ОУ и ДОС присутствует люфт (зазор) величиной 2Δ. Исследование отработки ступенчатых сигналов проводим с учетом насыщения УМ, но без учета люфта. На рисунке 3.1,б приведена характеристика нелинейного элемента (НЭ) типа «насыщение». ), а между ОУ и ДОС присутствует люфт (зазор) величиной 2Δ. Исследование отработки ступенчатых сигналов проводим с учетом насыщения УМ, но без учета люфта. На рисунке 3.1,б приведена характеристика нелинейного элемента (НЭ) типа «насыщение».

Рисунок 3.1 – Характеристика нелинейностей: а) люфт; б) ограничение
3.1 Исследование системы при подаче ступенчатого сигнала
Проанализируем влияние типовой нелинейности “насыщение” в УМ на переходные процессы в системе при подаче на вход ступенчатого сигнала величины  , ,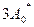 , , и 1 В. Нелинейность “люфт” при этом не учитывается. и 1 В. Нелинейность “люфт” при этом не учитывается.
Построим реакции нелинейной системы по выходу УМ и выходу ДОС на ступенчатый входной сигнал величины  , ,  , , 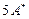 и на единичный с помощью моделирования соответствующей нелинейной системы в среде ППП VisSim. Здесь и на единичный с помощью моделирования соответствующей нелинейной системы в среде ППП VisSim. Здесь  В — наибольшая величина ступенчатого входа при которой УМ работает в зоне линейности (рассчитана в разделе 2.4). Графики переходных функций по выходу ДОС в нормированном виде изображены на рисунке 3.2. В — наибольшая величина ступенчатого входа при которой УМ работает в зоне линейности (рассчитана в разделе 2.4). Графики переходных функций по выходу ДОС в нормированном виде изображены на рисунке 3.2.

1 – А*
, 2 – 3А*
, 3 – 5 А*
, 4 – единичный сигнал
Рисунок 3.2 – Реакция системы по выходу ДОС на ступенчатые сигналы
В нашем случае влияние нелинейности слабо прослеживается при воздействии входных сигналов равных 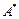 , ,  , , 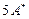 . Для исследования построим дополнительные графики при входных сигналах равных 100 . Для исследования построим дополнительные графики при входных сигналах равных 100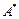 , 200 , 200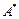 , 1000 , 1000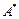 . Их графики приведены на рисунке 3.3. . Их графики приведены на рисунке 3.3.

1 -  , 2 - , 2 -  , 3 - , 3 -  , 4 - , 4 - 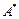
Рисунок 3.3 – Реакция системы по выходу ДОС на ступенчатые сигналы
(дополнительные построения)

1 – А*
, 2 – 3 А*
, 3 – 5 А*
, 4 – единичный сигнал
Рисунок 3.4 – Реакция системы на ступенчатые сигналы по выходу УМ
При росте амплитуды входного сигнала увеличивается время регулирования. Это отличает нелинейную систему от линейной. В линейной системе амплитуда входного сигнала не влияет на скорость протекания переходных процессов.
По полученным переходным функциям по выходу ДОС определим прямые показатели качества перерегулирование  и время переходного процесса и время переходного процесса  : :
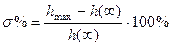 . .
Значения прямых показателей качества при воздействии на нелинейную систему рассматриваемых входных сигналов, а также прямых показателей качества соответствующих линейной системе, найденных в разделе 2.3, приведены в таблице 3.1.
Таблица 3.1 – Сравнение прямых показателей качества
| Тип системы |
Входной сигнал, В |
 ,с ,с |
 |
С учетом
ограничения УМ
|
1 |
0.166 |
20.8 |
| А*
= 0.074 |
0.151 |
31.0 |
| 3А*
= 0.222 |
0.165 |
20.7 |
| 5А*
= 0.37 |
0.201 |
16.4 |
| 100А*
= 7.4 |
0.579 |
15.2 |
| 200А*
= 44.4 |
0.871 |
13.3 |
| 1000А*
= 74 |
2.764 |
2.81 |
| Линейная САУ |
1 |
0.151 |
31.0 |
Проанализируем полученные данные.
При входном воздействии 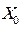 прямые показатели качества нелинейной системы с учетом насыщения УМ совпадают с прямыми показателями качества линейной системы. Это связано с тем, что нелинейная система при величинах входного сигнала меньших или равных прямые показатели качества нелинейной системы с учетом насыщения УМ совпадают с прямыми показателями качества линейной системы. Это связано с тем, что нелинейная система при величинах входного сигнала меньших или равных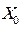 работает в зоне линейности УМ, т.е. ведет себя как линейная. работает в зоне линейности УМ, т.е. ведет себя как линейная.

Рисунок 3.5 – Линеаризация нелинейности типа «ограничение» методом секущих
Опираясь на метод линеаризации по секущей и то, что коэффициент передачи системы определяет собой наклон линейной характеристики звена, можно попытаться выявить влияние величины входного сигнала на величины прямых показателей качества.
С ростом величины входного сигнала уменьшается угол наклона линейной характеристики системы, а, следовательно, уменьшается коэффициент передачи системы. Уменьшение коэффициента передачи системы приведет к тому, что ЛАХ системы (см. рисунок 2.1) опустится вниз. Это приведет к уменьшению частоты среза, а, следовательно, к увеличению времени протекания переходного процесса. В то же время, запасы устойчивости системы увеличатся, так как ЛФХ при уменьшении коэффициента регулирования не меняет своего положения. Но, в то же время, ЛАХ попадает в запрещенную область, а это свидетельствует о невыполнении требовании ТЗ.
Если коэффициент передачи усилителя мощности снизился, то общий коэффициент передачи разомкнутого контура также снизился, а значит ЛАХ разомкнутого контура сдвинулась вниз. Это влечет за собой уменьшение частоты среза, причем она также уменьшается тем сильнее, чем больше поданное на вход системы значение ступенчатого сигнала. Так как изменяется частота среза, то изменяется и запас устойчивости по фазе, который, как известно, рассчитывается именно на частоте среза. Судя по рисунку 2.1, при уменьшении частоты среза сначала запас устойчивости по фазе растет, затем есть небольшой отрезок ЛФХ, при котором запас устойчивости уменьшается, а затем он снова растет. Это отражается на колебательности системы, а так же на перерегулировании: сначала перерегулирование, соответственно, уменьшается, затем – увеличивается, а затем снова уменьшается (это хорошо видно на рисунках 3.2 и 3.4). Время регулирования увеличивается по мере роста амплитуды входного сигнала и, соответственно, уменьшения коэффициента усиления УМ.
Рассмотрим теперь реакцию системы по выходу УМ. На рисунке 3.4 изображены графики переходных функций по выходу УМ при различных ступенчатых воздействиях, полученные в ППП VisSim. Как видно из рисунка, величина выходного сигнала УМ не может превысить значения 110 В.
Как уже было отмечено выше, при ступенчатых входных воздействиях величиной, большей, чем А*
, начинают сказываться нелинейные свойства системы, что приводит к ухудшению быстродействия системы.
3.2 Исследование возможных автоколебаний в автономной САР
Для исследования возможных автоколебаний применятся частотный метод определения автоколебаний Л.С.Гольдфарба. Однако следует отметить, что он применяется для линеаризованной системы. Следовательно, перед его использованием нам надо воспользоваться одним из методов линеаризации системы. Наиболее удобным математическим аппаратом является метод гармонической линеаризации нелинейностей.
Суть метода гармонической линеаризации состоит в замене нелинейного элемента эквивалентным линейным. Условиями эквивалентности служат совпадения выходных колебаний линейного звена с первой гармоникой выходных колебаний нелинейного звена, когда на их вход подается гармонический сигнал вида x =
Asin(
w
t).
Если характеристика нелинейного элемента однозначная и симметричная относительно начала координат, то эквивалентный линейный элемент может описываться уравнением.
 (3.1) (3.1)
где x
- входная координата; у
- выходная координата;  - коэффициент гармонической линеаризации. - коэффициент гармонической линеаризации.
В случае неоднозначных (петлевых) нелинейностей первая гармоника входного сигнала сдвинута по фазе относительно входного сигнала; этой же способностью должен обладать эквивалентный линейный элемент, поэтому при линеаризации используется элемент, свойства которого определяются уравнением
 (3.2) (3.2)
где, q(a)
и q’(a)
- коэффициенты гармонической линеаризации, определяемые только для данной нелинейности, которые должны обеспечить равенство между выходными колебаниями эквивалентного линейного и первой гармоникой нелинейного элемента.
Передаточная функция в данном случае выражается
 (3.3) (3.3)
Частотная характеристика:
 (3.4) (3.4)
Коэффициенты гармонической линеаризации могут зависеть и от частоты, тогда частотная характеристика нелинейного элемента примет вид
 (3.5) (3.5)
Опишем суть частотного метода Гольдфарба. Признак нахождения системы на границе устойчивости записывается как
 (3.6) (3.6)
Для применения метода логарифмических характеристик выражение (3.6) логарифмируется, и исходные уравнения записываются в виде
 (3.7) (3.7)
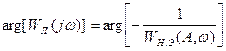 (3.8) (3.8)
Решение определяется графически, т.е. надо найти такие значения  и и 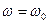 , при которых одновременны имеют место сразу оба равенства. Для этой цели строится ФГУ по следующему правилу. Точки пересечения амплитудной характеристики линейной части с амплитудными характеристиками нелинейной части сносятся на вертикали, на соответствующие фазовые характеристики нелинейной части; через полученные таким образом точки проводиться ФГУ. Таким же образом строится АГУ. Для практического определения устойчивости автоколебаний на ФГУ и АГУ следует нанести штриховку с одной стороны по одному из следующих правил: , при которых одновременны имеют место сразу оба равенства. Для этой цели строится ФГУ по следующему правилу. Точки пересечения амплитудной характеристики линейной части с амплитудными характеристиками нелинейной части сносятся на вертикали, на соответствующие фазовые характеристики нелинейной части; через полученные таким образом точки проводиться ФГУ. Таким же образом строится АГУ. Для практического определения устойчивости автоколебаний на ФГУ и АГУ следует нанести штриховку с одной стороны по одному из следующих правил:
а) если при увеличении амплитуды  амплитудные характеристики нелинейной части перемещаются вниз, то ФГУ штрихуется снизу и наоборот; амплитудные характеристики нелинейной части перемещаются вниз, то ФГУ штрихуется снизу и наоборот;
б) если перемещается вдоль ФГУ в сторону увеличения амплитуды  , то штриховка должна быть справа. , то штриховка должна быть справа.
в) в окрестности точки пересечения уточнить направление возрастания амплитуды А
, при возрастании амплитуды АГУ штрихуется слева.
После нанесения штриховки используется следующий признак: автоколебания устойчивы, если фазовая характеристика линейной части 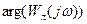 при перемещении по ней в сторону увеличения частоты пересекает ФГУ, переходя с заштрихованной стороны на незаштрихованную. Такое же правило справедливо и для АГУ. при перемещении по ней в сторону увеличения частоты пересекает ФГУ, переходя с заштрихованной стороны на незаштрихованную. Такое же правило справедливо и для АГУ.
Определение возможности возникновения автоколебаний в системе с учетом насыщения в усилителе мощности.
Для нелинейного звена с однозначной характеристикой:
 (3.9) (3.9)
Следовательно,
 (3.10) (3.10)
Логарифмические характеристики  имеют следующий вид: имеют следующий вид:
 , (3.11) , (3.11)
 . (3.12) . (3.12)
Во всех случаях, когда возможно определение свойств нелинейного звена в функции приведённой амплитуды 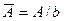 , где , где  параметр нелинейности, в приведённых выше выражениях параметр нелинейности, в приведённых выше выражениях  заменяется на заменяется на  . Видно, что характеристики нелинейного звена не зависят от . Видно, что характеристики нелинейного звена не зависят от  и представляют собой семейства горизонтальных линий. Коэффициент гармонической линеаризации для нелинейности типа «ограничение» определяется следующим образом и представляют собой семейства горизонтальных линий. Коэффициент гармонической линеаризации для нелинейности типа «ограничение» определяется следующим образом
 (3.13) (3.13)
ФГУ для данного типа нелинейности представляет собой отрезок линий -180 , ограниченный справа частой среза , ограниченный справа частой среза  . АГУ (амплитудная граница устойчивости) есть вертикальная линия на частоте . АГУ (амплитудная граница устойчивости) есть вертикальная линия на частоте   . .
Так как ЛФХ линейной системы и ФГУ не пересекаются, то автоколебания при данном типе нелинейности в проектируемой системе отсутствуют.
Для возникновения автоколебаний нужно поднять ЛАХ скорректированной разомкнутой системы на расстояние 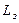 = 13 дБ, а для этого необходимо увеличить коэффициент усиления разомкнутой системы К в = 13 дБ, а для этого необходимо увеличить коэффициент усиления разомкнутой системы К в  раз до критического значения раз до критического значения  . В этом случае линейная система будет на границе устойчивости, а ЛАХ будет пересекать АГУ из заштрихованной области в незаштрихованную в одной точке, следовательно будут возникать устойчивые автоколебания. . В этом случае линейная система будет на границе устойчивости, а ЛАХ будет пересекать АГУ из заштрихованной области в незаштрихованную в одной точке, следовательно будут возникать устойчивые автоколебания.
Определим возможность возникновения автоколебаний в системе с учетом люфта в кинематической передаче.
Нелинейное звено типа люфт является нелинейностью гистерезисного типа и имеет зону нечувствительности. Так как  , коэффициенты , коэффициенты  данной нелинейности при данной нелинейности при 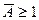 определяются выражениями: определяются выражениями:
 , при , при  , (3.14) , (3.14)
 , при , при  , (3.15) , (3.15)
 , (3.16) , (3.16)
 . (3.17) . (3.17)
Данные для построения ФГУ при данной нелинейности возьмём из приложения В.
На рисунке 3.4 показаны ЛАХ и ЛФХ линейной части системы и ФГУ и АГУ. Видно, что имеется пересечение ФГУ с фазовой характеристикой системы и АГУ с ЛАХ системы, следовательно, делаем вывод, что при наличии люфта автоколебания существуют. Причем устойчивыми они будут лишь в том случае, когда фазовая характеристика линейной части, при перемещении по ней в сторону увеличения  , будет пересекать фазовую границу устойчивости, переходя из заштрихованной части в незаштрихованную. , будет пересекать фазовую границу устойчивости, переходя из заштрихованной части в незаштрихованную.
Имеется 2 точки пересечения ЛФХ линейной части системы с ФГУ и ЛАХ с АГУ. Они изображены на рисунке 3.4. Амплитуда колебаний в данном случае  с частотой с частотой 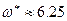 рад/с. рад/с.
Условием возникновения автоколебаний является пересечение АГУ с ЛАХ линейной системы. Изменяя коэффициент усиления разомкнутой системы можно сдвигать ЛАХ линейной системы вертикально, и найти такой коэффициент усиления разомкнутой системы, при котором ее ЛАХ будет касаться АГУ (граница существования автоколебаний). Таким образом, можно подобрать такое значение  , при котором в системе не будет наблюдаться автоколебаний. , при котором в системе не будет наблюдаться автоколебаний.
Расстояние  , на которое нужно сместить ЛАХ, чтобы она не пересекала АГУ. По рисунку приближенно определим значение , на которое нужно сместить ЛАХ, чтобы она не пересекала АГУ. По рисунку приближенно определим значение  : :
 дБ. дБ.
Используя полученное значение, можно приближенно определить значение коэффициента усиления, при котором автоколебания исчезают:

При низких частотах АГУ пересечет ЛАХ (и ЛФХ пересечет ФГУ) линейной части еще в одной точке, однако автоколебания на данной частоте не возникнут, так как в этом случае ЛФХ линейной системы при увеличении частоты переходит с незаштрихованной стороны ФГУ в заштрихованную.
Заключение
В ходе работы было синтезировано автоматическое управляющее устройство (регулятор), которое позволяет системе достичь требуемого в ТЗ качества.
После этого скорректированная САР исследовалась на качество. Были рассмотрены частотные, корневые, прямые показатели качества. По всем показателям качества скорректированная система имеет приемлемые значения.
В пункте 2 были построены области устойчивости и заданного качества для проектируемой САР.
В 3 пункте рассматривалась отработка нелинейной системой ступенчатого сигнала, начального рассогласования и гармонического сигнала. Проанализировано влияние нелинейностей «насыщение» и «люфт» на протекание процессов в системе. При наличии нелинейностей были исследованы возможные режимы автоколебаний. В полученной САР автоколебания вызываются только нелинейностью типа «люфт». Была исследована возможность появления устойчивых автоколебаний в данной системе.
Библиографический список
1. Зырянов, Г.В. Динамический синтез САУ: Учебное пособие по выполнению курсовой работы / Г.В.Зырянов, А.А Кощеев. – Челябинск: ЮУрГУ, 2001.
2. Бесекерский, В.А. Теория автоматического управления / В.А. Бесекерский, Е.П. Попов. – Спб.: Профессия, 2003.
3. Теория автоматического управления / Под ред. В.Б. Яковлева.– М.: ВШ, 2005.
4. Зырянов, Г.В. Линейные дискретные системы управления. – Челябинск, ЮУрГУ, 2005.
Приложения
Приложение А
Анализ линейной САР с пропорциональным законом регулирования
 Рисунок А.1 – Схема моделирования в ППП VisSim Рисунок А.1 – Схема моделирования в ППП VisSim
Рисунок А.2 – Нахождение корней A
(p
) в программе MathCad

Рисунок А.3 – Построение ВЧХ в программе MathCad
Приложение Б
Динамический синтез и исследование скорректированной САР
 Рисунок Б.1 – Исследование ПП скорректированной системы Рисунок Б.1 – Исследование ПП скорректированной системы
 Рисунок Б.2 – Нахождение корней A
(p
) в программе MathCad Рисунок Б.2 – Нахождение корней A
(p
) в программе MathCad

Рисунок Б.3 – Исследование УМ оптимизированной системы

Рисунок Б.4 – Построение ВЧХ скорректированной системы
Приложение В
Анализ влияния нелинейностей
Таблица В.1 – Данные для построения ОЭККП для нелинейности «люфт»
| a
|
Lm
(а
), дБ |
ψн
(а
), град |
a
|
Lm
(а
), дБ |
ψн
(а
), град |
| 1.010 |
38.00 |
–98 |
1.4 |
9.10 |
–132 |
| 1.020 |
32.07 |
–101 |
1.5 |
7.82 |
–136 |
| 1.030 |
28.64 |
–103 |
1.6 |
6.85 |
–139 |
| 1.040 |
26.24 |
–105 |
1.8 |
5.48 |
–144 |
| 1.050 |
24.39 |
–107 |
2.0 |
4.54 |
–148 |
| 1.060 |
22.90 |
–108 |
2.5 |
3.14 |
–154 |
| 1.075 |
21.10 |
–110 |
3.0 |
2.35 |
–158 |
| 1.100 |
18.82 |
–113 |
4.0 |
1.52 |
–163 |
| 1.150 |
15.73 |
–118 |
5.0 |
1.10 |
–167 |
| 1.200 |
13.64 |
–122 |
10.0 |
0.40 |
–173 |
| 1.250 |
12.09 |
–125 |
20.0 |
0.15 |
–176 |
| 1.300 |
10.89 |
–128 |
40.0 |
0.05 |
–178 |
|