МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Московский Авиационный институт
(Государственный технический университет)
«МАИ»
Кафедра 804
Курсовая работа по курсу
«Теория вероятностей и математическая статистика»
На тему «Метод наименьших квадратов»
Выполнила курсовую работу
студентка группы 05-206
Зуева Татьяна Анатольевна
Дата сдачи КР
Проверил курсовую работу
Шин Галина Захаровна
Москва 2005
Оглавление
1.
Исходные данные………………………………………………….3
2.
Постановка задачи…………………………………………………4
3.
Теоретическая часть……………………………………………….5
4.
Расчетная часть……………………………………………………10
5.
График …………………………………………………………….16
6.
Приложение………………………………………………………..17
7.
Список литературы……………………………………………… 18
1.Исходные данные
| Номер
|
Время X
|
Величина Y
|
| 1 |
-1 |
6,323 |
| 2 |
-0,95 |
-22,817 |
| 3 |
-0,9 |
-24,908 |
| 4 |
-0,85 |
20,708 |
| 5 |
-0,8 |
9,145 |
| 6 |
-0,75 |
-1,283 |
| 7 |
-0,7 |
39,694 |
| 8 |
-0,65 |
-16,954 |
| 9 |
-0,6 |
29,198 |
| 10 |
-0,55 |
-43,22 |
| 11 |
-0,5 |
11,371 |
| 12 |
-0,45 |
-5,745 |
| 13 |
-0,4 |
11,171 |
| 14 |
-0,35 |
1,058 |
| 15 |
-0,3 |
-15,19 |
| 16 |
-0,25 |
-45,976 |
| 17 |
-0,2 |
-0,25 |
| 18 |
-0,15 |
-18,76 |
| 19 |
-0,1 |
14,7 |
| 20 |
-0,05 |
-17,959 |
| 21 |
0 |
-0,377 |
| 22 |
0,05 |
-12,988 |
| 23 |
0,1 |
55,728 |
| 24 |
0,15 |
-2,009 |
| 25 |
0,2 |
-4,523 |
| 26 |
0,25 |
-11,937 |
| 27 |
0,3 |
-17,419 |
| 28 |
0,35 |
1,564 |
| 29 |
0,4 |
12 |
| 30 |
0,45 |
-25,92 |
| 31 |
0,5 |
29,946 |
| 32 |
0,55 |
-27,554 |
| 33 |
0,6 |
-6,12 |
| 34 |
0,65 |
-5,25 |
| 35 |
0,7 |
-7,488 |
| 36 |
0,75 |
-29,674 |
| 37 |
0,8 |
-34,196 |
| 38 |
0,85 |
-0,239 |
| 39 |
0,9 |
4,966 |
| 40 |
0,95 |
-5,11 |
| 41 |
1 |
-7,541 |
Постановка задачи
а).Задано множество пар значений {(xt
,yt
)}, t= (n=41), представляющих собой результаты измерений функции. Дан прибор, который генерирует функцию y(x)=ax+b. На вход поступает сигнал x1
,x2
,..,xn
; на выходе: y1
,y2
,…,yn
. (n=41), представляющих собой результаты измерений функции. Дан прибор, который генерирует функцию y(x)=ax+b. На вход поступает сигнал x1
,x2
,..,xn
; на выходе: y1
,y2
,…,yn
.
Числа не соответствуют внутренним числам, так как прибор имеет шумы
yt
=axt
+b +εt
, t= , ,
где a,b – неизвестные коэффициенты, а εt
– независимые в совокупности случайные величины с нормальным законом распределения: εt
~N(0,σ2
), где σ2
неизвестная дисперсия; 0 – математическое ожидание шума εt
.
М εt
=0, в εt
= σ2
.
Требуется найти методом наименьших квадратов неизвестные параметры кривой регрессии.
y(x)=ax+b– кривая регрессии – условное матожидание случайной величины Y при аргументе x, М(y/x).
б). Построить график линии регрессии ỹ(x).
- Найти точечную оценку для неизвестного параметра
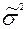 неизвестной дисперсии σ2
, которая входит в нормальный закон распределения. неизвестной дисперсии σ2
, которая входит в нормальный закон распределения.
- Построить интервальные оценки для неизвестных коэффициентов a,b и дисперсии σ2
на уровне доверия j1
=0,9; j2
=0,95.
- С помощью критерия Снедекера-Фишера проверить гипотезу Ho
: a=0 и гипотезу Ho
: b=0 на уровне доверия j1
=0,9 и j2
=0,95.
Теоретическая часть
1.Выборка.
Математическая статистика – наука о математических методах, позволяющих по статистическим данным, например по реализациям случайной величины (СВ), построить теоретико-вероятностную модель исследуемого явления. Задачи математической статистики являются, в некотором смысле, обратными к задачам теории вероятностей. Центральным понятием математической статистики является выборка.
Определение 1.
Однородной выборкой (выборкой)
объема n при n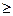 1 называется случайный вектор Zn
=col(X1
,…,Xn
), компоненты которого Xi
, i= 1 называется случайный вектор Zn
=col(X1
,…,Xn
), компоненты которого Xi
, i= , называемые элементами выборки, являются независимыми СВ с одной и той же функцией распределения F(x). Будем говорить, что выборка Zn
соответствует функции распределения F(x). , называемые элементами выборки, являются независимыми СВ с одной и той же функцией распределения F(x). Будем говорить, что выборка Zn
соответствует функции распределения F(x).
Числа, данные, полученные после опыта – апостериорная выборка.
Определение 2.
Реализацией
выборки называется неслучайный вектор zn
=col(x1
,…,xn
), компонентами которого являются реализации соответствующих элементов выборки Xi
, i= . .
Из этих определений вытекает, что реализацию выборки zn можно также рассматривать как последовательность x1,…,xnиз n реализаций одной и той же СВ X, полученных в серии из nнезависимых одинаковых опытов, проводимых в одинаковых условиях. Поэтому можно говорить, что выборка Zn порождена наблюдаемой СВ X, имеющей распределение Fx
(x)=F(x).
Определение 3.
Если компоненты вектора Zn независимы, но их распределения F1
(x1
),…,Fn
(xn
) различны, то такую выборку называют неоднородной.
Определение 4.
Множество Sвсех реализаций выборки Zn
называется выборочным пространством.
Выборочное пространство может быть всем n-мерным евклидовым пространством Irn или его частью, если СВ X непрерывна, а также может состоять из конечног или счетного числа точек из Irn, если СВ X дискретна.
На практике при исследовании конкретного эксперимента распределения F1
(x1
),…,Fn
(xn
) СВ X1
,…,Xn
редко бывают известны полностью. Часто априори (до опыта) можно лишь утверждать, что распределение FZn
(zn
)=F1
(x1
),…Fn
(xn
) случайного вектора Zn
принадлежит некоторому классу (семейству) F.
Определение 5.
Пара (S,F) называется статистической моделью описания
серии опытов, порождающих выборку Zn
.
Определение 6.
Если распределение FZn
(zn
,Ө
) из класса F определены с точностью до некоторого векторного параметра Ө
 Θ Θ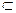 IRs
, то такая статистическая модель называется параметрической
и обозначается (SӨ
,
FZn
(
zn
, Ө
)), Ө IRs
, то такая статистическая модель называется параметрической
и обозначается (SӨ
,
FZn
(
zn
, Ө
)), Ө
 Θ Θ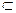 IRs
. IRs
.
В некоторых случаях выборочное пространство может не зависеть от неизвестного параметра Ө
распределения FZn
(zn
,Ө
).
В зависимости от вида статистической модели в математической статистике формулируются соответствующие задачи по обработке информации, содержащейся в выборке.
Определение 7.
СВ Z=φ(Zn
), где φ(Zn
) – произвольная функция, определенная на выборочном пространстве S и не зависящая от распределения FZn
(zn
,Ө
), называется статистикой.
2. Точечные оценки.
Определение 2.1.
Параметром
распределения Ө
 Θ Θ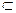 IR1
СВ X называется любая числовая характеристика этой СВ ( математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения. IR1
СВ X называется любая числовая характеристика этой СВ ( математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения.
В общем случае будем предполагать, что параметр распределения Ө
может быть векторным, т.е. Ө
 Θ Θ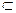 IRs
. IRs
.
В случае параметрической статистической модели (SӨ
,
FZn
(
zn
,Ө
)) таким параметром распределения может служить неизвестный вектор Ө
 Θ Θ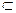 IRs
, характеризующий распределение FZn
(
zn
,Ө
). IRs
, характеризующий распределение FZn
(
zn
,Ө
).
Пусть имеется выборка Zn
=col(X1
,…Xn
) с реализацией zn
=(x1
,…xn
).
Определение 2.2.
Точечной (выборочной
) оценкой неизвестного параметра распределения Ө
 Θ Θ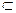 IRs
называется произвольная статистика IRs
называется произвольная статистика  (Zn
), построенная по выборке Zn
и принимающая значения в множестве Θ. (Zn
), построенная по выборке Zn
и принимающая значения в множестве Θ.
Замечание 2.1.
Реализацию  (zn
) оценки (zn
) оценки  (Zn
), принимают, как правило, за приближенное значение неизвестного параметра Ө
. (Zn
), принимают, как правило, за приближенное значение неизвестного параметра Ө
.
Ясно, что существует много разных способов построения точечной оценки которые учитывают тип статистической модели. Для параметрической и не параметрической моделей эти способы могут быть различны. Рассмотрим некоторые свойства, которые характеризуют качество введенной оценки.
Определение 2.3.
Оценка  (Zn
) параметра Ө
называется несмещенной
, если ее МО равно Ө
, т.е. M[ (Zn
) параметра Ө
называется несмещенной
, если ее МО равно Ө
, т.е. M[ (Zn
)]= Ө
для любого Ө (Zn
)]= Ө
для любого Ө
 Θ. Θ.
Определение 2.4.
Оценка  (Zn
) параметра Ө
называется состоятельной,
если она сходится по вероятности к Ө
, т.е. (Zn
) параметра Ө
называется состоятельной,
если она сходится по вероятности к Ө
, т.е.  (Zn
) (Zn
) Ө
при n → ∞ для любого Ө Ө
при n → ∞ для любого Ө
 Θ. Θ.
Определение 2.5.
Оценка  (Zn
) параметра Ө
называется сильно состоятельной
, если она сходится почти наверное к Ө
, т.е. (Zn
) параметра Ө
называется сильно состоятельной
, если она сходится почти наверное к Ө
, т.е.  (Zn
) (Zn
) Ө
при n → ∞ для любого Ө Ө
при n → ∞ для любого Ө
 Θ. Θ.
Определение 2.6.
Несмещенная оценка  *(Zn
) скалярного параметра Ө
называется эффективной
, если D[ *(Zn
) скалярного параметра Ө
называется эффективной
, если D[ *(Zn
)]≤ D[ *(Zn
)]≤ D[ (Zn
)] для всех несмещенных оценок (Zn
)] для всех несмещенных оценок  (Zn
) параметра Ө
, т.е. ее дисперсия минимальна по сравнению с дисперсиями других несмещенных оценок при одном и том же объеме n выборки Zn
. (Zn
) параметра Ө
, т.е. ее дисперсия минимальна по сравнению с дисперсиями других несмещенных оценок при одном и том же объеме n выборки Zn
.
Вообще говоря, дисперсии несмещенных оценок могут зависеть о параметра Ө.
В этом случае под эффективной оценкой понимается такая, для которой вышеприведенное неравенство является строгим хотя бы для одного значения параметра Ө.
3.Интервальные оценки.
Пусть имеется параметрическая статистическая модель (SӨ
,
FZn
(
zn
,Ө
)), Ө
 Θ Θ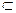 IR1
, и по выборке Zn
=col(X1
,…Xn
), соответствующей распределению F(
x,Ө
), наблюдаемой СВ X, требуется оценить неизвестный параметр Ө
. Вместо точечных оценок, рассмотренных ранее, рассмотрим другой тип оценок неизвестного параметра Ө IR1
, и по выборке Zn
=col(X1
,…Xn
), соответствующей распределению F(
x,Ө
), наблюдаемой СВ X, требуется оценить неизвестный параметр Ө
. Вместо точечных оценок, рассмотренных ранее, рассмотрим другой тип оценок неизвестного параметра Ө
 Θ Θ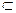 IR1
. IR1
.
Определение 3.1.
Интервал [θ1
(Zn
),θ2
(Zn
)] со случайными концами, «накрывающий» с вероятностью 1-α, 0<α<1, неизвестный параметр θ, т.е.
P{ θ1
(Zn
)≤ θ ≤ θ2
(Zn
)}= 1-α,
называется доверительным интервалом (или интервальной оценкой
) уровня надежности 1-α параметра θ.
Аналогично определяется доверительный интервал для произвольной функции от параметра θ.
Определение 3.2.
Число δ=1-α называется доверительной вероятностью
или уровнем доверия (надежности).
Определение 3.3.
Доверительный интервал [θ1
(Zn
),θ2
(Zn
)] называется центральным
, если выполняются следующие условия:
P{ θ≥ θ2
(Zn
)}=  , P{ θ1
(Zn
) ≥ θ}= , P{ θ1
(Zn
) ≥ θ}= . .
Часто вместо двусторонних доверительных интервалов рассматривают односторонние доверительные интервалы, полагая θ1
(Zn
)= -∞ или θ2
(Zn
)= +∞.
Определение 3.4.
Интервал, границы которого удовлетворяют условию:
P{ θ≥ θ2
(Zn
)}= α (или P{ θ1
(Zn
) ≥ θ}= α.),
называется соответственно правосторонним (
или левосторонним)
доверительным интервалом.
4.Проверка статистических гипотез.
Определение 4.1.
Статистической гипотезой
H или просто гипотезой называется любое предположение относительно параметров ли законов распределения СВ X, проверяемое по выборке Zn
.
Определение 4.2.
Проверяемая гипотеза называется основной (
или нулевой
) и обозначается Ho. Гипотеза, конкурирующая с Ho
, называется альтернативной и обозначается H1
,
Определение 4.3.
Статистическая гипотеза Ho называется простой,
если она однозначно определяет параметр или распределение СВ X. В противном случае гипотеза Ho
называется сложной.
Определение 4.4.
Статистическим критерием
(критерием согласия, критерием значимости или решающим правилом) проверки гипотезы Ho
называется правило, в соответствии с которым по реализации z=φ(zn
) статистики Z гипотеза Ho
принимается или отвергается.
Определение 4.5.
Критической областью
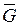 статистического критерия называют область реализации z статистики Z, при которых гипотеза Ho отвергается. статистического критерия называют область реализации z статистики Z, при которых гипотеза Ho отвергается.
Определение 4.6
. Доверительной областью
G статистического критерия называется область значений z статистики Z, при которых гипотеза Ho
принимается.
Например, в качестве статистического критерия можно использовать правило:
- Если значение z= φ(zn
) статистики Z= φ(zn
) лежит в критической области
 , то гипотеза Ho отвергается и принимается альтернативная гипотеза H1
; , то гипотеза Ho отвергается и принимается альтернативная гипотеза H1
;
- Если реализация z= φ(zn
) статистики Z= φ(zn
) лежит в доверительной области G, то гипотеза Ho
принимается.
При реализации этого правила возникают ошибки двух видов.
Определение 4.7
. Ошибкой 1-го рода
называется событие, состоящее в том, что гипотеза Ho
отвергается, когда она верна.
Определение 4.8
. Ошибкой 2-го рода
называется событие, состоящее в том, что принимается гипотеза Ho
, когда верна гипотеза H1
.
Определение 4.9
. Уровнем значимости
статистического критерия называется вероятность ошибки 1-го рода α=P{Z 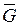 |Ho
}, Вероятность ошибки 1-го рода α может быть вычислено, если известно распределение F(z|Ho
) статистики Z. |Ho
}, Вероятность ошибки 1-го рода α может быть вычислено, если известно распределение F(z|Ho
) статистики Z.
Вероятность ошибки 2-го рода равна β=P{Z G|Ho
} и может быть вычислена, если известно условное распределение F(z|H1
) статистики Z при справедливости гипотезы H1
. G|Ho
} и может быть вычислена, если известно условное распределение F(z|H1
) статистики Z при справедливости гипотезы H1
.
Ясно. Что с уменьшением вероятности α ошибки 1-го рода возрастает вероятность β ошибки 2-го рода, и наоборот, т.е. при выборе критической и доверительной областей должен достигаться определенный компромисс. Поэтому часто при фиксированной вероятности ошибки 1-го рода критическая область выбирается таким образом, чобы вероятность ошибки второго рода была минимальна.
Определение 4.10.
Мощность статистического критерия
– это вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.
Проверка статистической гипотезы
может быть подразделена на следующие этапы:
- сформулировать проверяемую гипотезу Ho
и альтернативную к ней гипотезу H1
;
- выбрать уровень значимости α;
- выбрать статистику Z для проверки гипотезы Ho
;
- найти распределение F(z|Ho
) статистики Z при условии, что гипотеза Ho
верна;
- построить, в зависимости от формулировки гипотезы H1
и уровня значимости α, критическую область
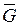 ; ;
- получить выборку наблюдений x1
,..,xn
и вычислить выборочное значение z= φ(x1
,..,xn
) статистики Z критерия;
- принять статистическое решение на уровне доверия 1-α: если Z
 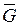 , то отклонить гипотезу Ho
как не согласующуюся с результатами наблюдений, а если Z , то отклонить гипотезу Ho
как не согласующуюся с результатами наблюдений, а если Z G, то принять гипотезу Ho
как не противоречащую результатам наблюдений. G, то принять гипотезу Ho
как не противоречащую результатам наблюдений.
Теория к лабораторной работе №3.
Определение 1
.Упорядочим элементы реализации выборки х1
,…,хn
по возрастанию: x(1)
≤x(2)
≤…≤x(n)
, где верхний индекс соответствует номеру элемента в упорядоченной последовательности.
Обозначим через x(k)
, k=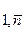 , случайные величины, которые при каждой реализации zn выборки Zn принимают k-е (по верхнему индексу) значения x(k). Упорядоченную последовательность случайных величин: x(1)
≤…≤x(n)
называют вариационным рядом выборки. , случайные величины, которые при каждой реализации zn выборки Zn принимают k-е (по верхнему индексу) значения x(k). Упорядоченную последовательность случайных величин: x(1)
≤…≤x(n)
называют вариационным рядом выборки.
Определение 2.
Элементы x(
k)
вариационного ряда называются порядковыми статистиками
, а крайние члены вариационного ряда x(1)
, x(
n)
– экстремальными порядковыми статистиками.
Определение 3
. Рассмотримпроцедуру группировки выборки. Для этого действительную ось IR1=(-∞,∞) разделим точками αо,…,αl+1
на l+1 непересекающихся полуинтервал (разряд) ∆k=[αk
, αk+1
), k=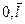 , таким образом, что -∞= αо< α1
<…< αl
< αl+1
=+∞, α1
≤ x(1)
, αl
≥ x(
n)
. Обычно длина разрядов ∆k, k= , таким образом, что -∞= αо< α1
<…< αl
< αl+1
=+∞, α1
≤ x(1)
, αl
≥ x(
n)
. Обычно длина разрядов ∆k, k= , выбирается одинаковой, т.е. равной hk=(αl-α1)/(l-1). Используя реализацию вариационного ряда x(1)
<…<x(
n)
, для каждого k-го разряда k= , выбирается одинаковой, т.е. равной hk=(αl-α1)/(l-1). Используя реализацию вариационного ряда x(1)
<…<x(
n)
, для каждого k-го разряда k= , вычислим частоту попадания элементов реализации выборки в этот разряд. Получаем , вычислим частоту попадания элементов реализации выборки в этот разряд. Получаем 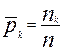 , где nk
- число элементов реализации выборки zn
, попавших в k-й разряд. Если рассмотреть априорную выборку Zn и случайное число Nk
элементов этой выборки, попавших в k-й разряд, то получим набор случайных величин , где nk
- число элементов реализации выборки zn
, попавших в k-й разряд. Если рассмотреть априорную выборку Zn и случайное число Nk
элементов этой выборки, попавших в k-й разряд, то получим набор случайных величин  . .
Последовательность пар ( ),k= ),k= , называется статистическим рядом
, а его реализация ( , называется статистическим рядом
, а его реализация ( ),k= ),k= представляется в виде таблицы: представляется в виде таблицы:
| [
α1, α2) |
…..
|
[
αl-1, αl] |
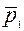
|
…..
|

|
Определение 4.
На оси OX отложим разряды и на них, как на основании, постоим прямоугольники с высотой, равной   , k= , k= . Тогда площадь каждого прямоугольника будет равна . Тогда площадь каждого прямоугольника будет равна  . Полученная фигура называется столбцовой диаграммой, а кусочно-постоянная функция . Полученная фигура называется столбцовой диаграммой, а кусочно-постоянная функция  , образованная верхними гранями полученных прямоугольников,- гистограммой
. , образованная верхними гранями полученных прямоугольников,- гистограммой
.
Определение 5.
Случайная величина X распределена равномерно
на отрезке [a,b] (X~R(a;b)), если плотность вероятности имеет вид:

Определение 6.
Случайная величина X имеет экспоненциальное (показательное)
распределение с параметром λ>0, т.е. X~E(λ), если плотность вероятности имеет вид:
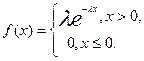
Определение 7
. Случайная величина X имеет нормальное (гауссовское)
распределение с параметрами m и σ2
>0, т.е. X~N(m; σ2
), если
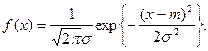
При этом случайная величина называется нормальной (гауссовской). График плотности нормального распределения, называемый кривой Гаусса, имеет единственный максимум в точке x=m.
Критерий согласия (критерий Пирсона).
Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Для выяснения их пользуются «критериями согласия». Одним из наиболее применяемых- является так называемый «критерий  » Пирсона. » Пирсона.

Расчетная часть.
1.Построение оценок и и  неизвестных коэффициентов. неизвестных коэффициентов.
Суть метода наименьших квадратов состоит в том, что  и и  находятся из условия минимума функции S(a,b): находятся из условия минимума функции S(a,b):
S(a,b)= , где n=41. , где n=41.
| № п
/
п
|
X
i
|
Y
i
|
X
2
|
XY
|
 xi
+
xi
+
|
 
|

|
| 1 |
-1 |
6,323 |
1 |
-6,323 |
0,697624 |
5,625376 |
31,64486 |
| 2 |
-0,95 |
-22,817 |
0,9025 |
21,67615 |
0,462944 |
-23,2799 |
541,9558 |
| 3 |
-0,9 |
-24,908 |
0,81 |
22,4172 |
0,228264 |
-25,1363 |
631,8318 |
| 4 |
-0,85 |
20,708 |
0,7225 |
-17,6018 |
-0,00642 |
20,71442 |
429,087 |
| 5 |
-0,8 |
9,145 |
0,64 |
-7,316 |
-0,2411 |
9,386096 |
88,0988 |
| 6 |
-0,75 |
-1,283 |
0,5625 |
0,96225 |
-0,47578 |
-0,80722 |
0,65161 |
| 7 |
-0,7 |
39,694 |
0,49 |
-27,7858 |
-0,71046 |
40,40446 |
1632,52 |
| 8 |
-0,65 |
-16,954 |
0,4225 |
11,0201 |
-0,94514 |
-16,0089 |
256,2837 |
| 9 |
-0,6 |
29,198 |
0,36 |
-17,5188 |
-1,17982 |
30,37782 |
922,8117 |
| 10 |
-0,55 |
-43,22 |
0,3025 |
23,771 |
-1,4145 |
-41,8055 |
1747,7 |
| 11 |
-0,5 |
11,371 |
0,25 |
-5,6855 |
-1,64918 |
13,02018 |
169,525 |
| 12 |
-0,45 |
-5,745 |
0,2025 |
2,58525 |
-1,88386 |
-3,86114 |
14,90843 |
| 13 |
-0,4 |
11,171 |
0,16 |
-4,4684 |
-2,11854 |
13,28954 |
176,6118 |
| 14 |
-0,35 |
1,058 |
0,1225 |
-0,3703 |
-2,35322 |
3,411216 |
11,63639 |
| 15 |
-0,3 |
-15,19 |
0,09 |
4,557 |
-2,5879 |
-12,6021 |
158,813 |
| 16 |
-0,25 |
-45,976 |
0,0625 |
11,494 |
-2,82258 |
-43,1534 |
1862,218 |
| 17 |
-0,2 |
-0,25 |
0,04 |
0,05 |
-3,05726 |
2,807256 |
7,880685 |
| 18 |
-0,15 |
-18,76 |
0,0225 |
2,814 |
-3,29194 |
-15,4681 |
239,261 |
| 19 |
-0,1 |
14,7 |
0,01 |
-1,47 |
-3,52662 |
18,22662 |
332,2095 |
| 20 |
-0,05 |
-17,959 |
0,0025 |
0,89795 |
-3,7613 |
-14,1977 |
201,5748 |
| 21 |
0 |
-0,377 |
0 |
0 |
-3,99598 |
3,618976 |
13,09698 |
| 22 |
0,05 |
-12,988 |
0,0025 |
-0,6494 |
-4,23066 |
-8,75734 |
76,69108 |
| 23 |
0,1 |
55,728 |
0,01 |
5,5728 |
-4,46534 |
60,19334 |
3623,238 |
| 24 |
0,15 |
-2,009 |
0,0225 |
-0,30135 |
-4,70002 |
2,691016 |
7,241564 |
| 25 |
0,2 |
-4,523 |
0,04 |
-0,9046 |
-4,9347 |
0,411695 |
0,169493 |
| 26 |
0,25 |
-11,937 |
0,0625 |
-2,98425 |
-5,16938 |
-6,76762 |
45,80074 |
| 27 |
0,3 |
-17,419 |
0,09 |
-5,2257 |
-5,40406 |
-12,0149 |
144,3589 |
| 28 |
0,35 |
1,564 |
0,1225 |
0,5474 |
-5,63874 |
7,202735 |
51,8794 |
| 29 |
0,4 |
12 |
0,16 |
4,8 |
-5,87342 |
17,87342 |
319,459 |
| 30 |
0,45 |
-25,92 |
0,2025 |
-11,664 |
-6,1081 |
-19,8119 |
392,5116 |
| 31 |
0,5 |
29,946 |
0,25 |
14,973 |
-6,34278 |
36,28878 |
1316,875 |
| 32 |
0,55 |
-27,554 |
0,3025 |
-15,1547 |
-6,57746 |
-20,9765 |
440,0154 |
| 33 |
0,6 |
-6,12 |
0,36 |
-3,672 |
-6,81214 |
0,692135 |
0,479051 |
| 34 |
0,65 |
-5,25 |
0,4225 |
-3,4125 |
-7,04682 |
1,796815 |
3,228545 |
| 35 |
0,7 |
-7,488 |
0,49 |
-5,2416 |
-7,2815 |
-0,2065 |
0,042644 |
| 36 |
0,75 |
-29,674 |
0,5625 |
-22,2555 |
-7,51618 |
-22,1578 |
490,9692 |
| 37 |
0,8 |
-34,196 |
0,64 |
-27,3568 |
-7,75086 |
-26,4451 |
699,3457 |
| 38 |
0,85 |
-0,239 |
0,7225 |
-0,20315 |
-7,98554 |
7,746535 |
60,0088 |
| 39 |
0,9 |
4,966 |
0,81 |
4,4694 |
-8,22021 |
13,18621 |
173,8763 |
| 40 |
0,95 |
-5,11 |
0,9025 |
-4,8545 |
-8,45489 |
3,344895 |
11,18832 |
| 41 |
1 |
-7,541 |
1 |
-7,541 |
-8,68957 |
1,148575 |
1,319224 |
| Результаты |
0
|
-163,835
|
14,35
|
-67,3532
|
17329,02
|
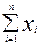
|

|

|

|

|
1.1 Составим систему нормальных уравнений: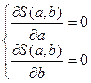 ,
решив эту систему, найдем ,
решив эту систему, найдем  и и  . .

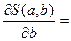 
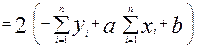


 =163,835/41= -3,99598; =163,835/41= -3,99598;
 = -67,3532/14,35= -4,6936. = -67,3532/14,35= -4,6936.
1.2 Построение оценки  при условии, что b=0. при условии, что b=0.

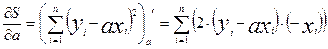
 =0 =0

67,3532+14,35а=0
ã = - 4,6936
1.3 Построение оценки  при условии, что а=0. при условии, что а=0.
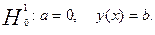

 =0 =0
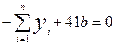
163,835+41b=0
b= - 3,99598
2.Построение оценки 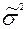 неизвестной дисперсии σ2
шумов
εt
. неизвестной дисперсии σ2
шумов
εt
.
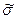 2
=
2
= , где S2
=(y-ỹ)T
*( y-ỹ), n=41(число измерений), m=2(количество неизвестных параметров). , где S2
=(y-ỹ)T
*( y-ỹ), n=41(число измерений), m=2(количество неизвестных параметров).
n - m=41-2=39
S2
=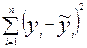 , где , где  - оценка кривой регрессии, - оценка кривой регрессии,  = = xi
+ xi
+
S2
= 17329,02;
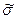 2
=
2
= =444,334
=444,334
  = -4,6936X- 3,99598 = -4,6936X- 3,99598
3.
Построение интервальных оценок коэффициентов
a
,
b
и дисперсии
s
2
на уровне доверия 0,9 и 0,95.
 , ,
где 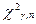 - квантиль уровня - квантиль уровня 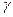 для для  - распределения с n степенями свободы. - распределения с n степенями свободы.
Квантили распределения  для интервала для интервала 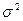 : :
а). , , 
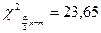

б).  , , 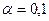
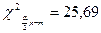

I.1.Построим интервальные оценки дисперсии
s2
на уровне доверия
g=0,95:
a=1-g=0,05,
 , ,
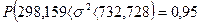 . .
2.Построим интервальные оценки дисперсии
s2
на уровне доверия
g=0,9:
a=1-g=0,1,

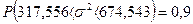
Далее, 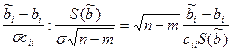 ~t(n-m), ~t(n-m),
где cii
обозначает (i,i)-ый элемент матрицы А-1
, а символ t(n-m) – распределение Стьюдента с n-m степенями свободы. Отсюда
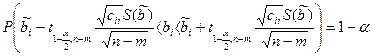 , ,
где  - квантиль уровня - квантиль уровня 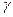 для распределения Стьюдента с n степенями свободы. для распределения Стьюдента с n степенями свободы.
Квантили распределения Стьюдента для интервалов a,b:
а).  , , 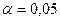 
б).  , , 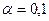 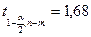
 , ,
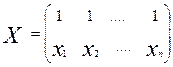 , ,

С11
=0,02439 (для свободного члена,b), С22
=0,069686 (для a).
n=41,
m=2.
II.1. Построим интервальную оценку для коэффициента
b на уровне доверия
g=0,95:
 , ,
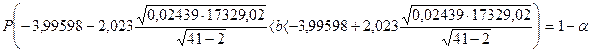

2.
Построим интервальную оценку для коэффициента
b на уровне доверия
g=0,9:
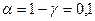 , ,

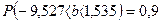 . .
III. 1.
Построим интервальную оценку для коэффициента
a на уровне доверия
g=0,95:
 , ,


2. Построим интервальную оценку для коэффициента
a на уровне доверия
g=0,9:
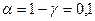 , ,

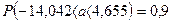
4.Проверка гипотез с помощью критерия Снедекера-Фишера.
Ho - разные гипотезы, H1
- альтернативная гипотеза.
Существует область принятия гипотезы и область отклонения гипотезы.
y(x)=ax+b
МНК: 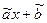
Необходимо проверить следующие гипотезы:
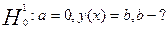
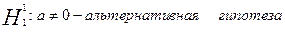 , ,
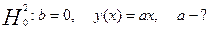
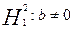
Критерий Снедекера-Фишера:
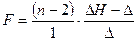 , где , где 
D=17329,02;
n=41.
Квантили распределения Фишера для критерия Снедекера-Фишера
а).  , , 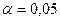 
б).  , , 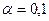 
1. y=b:  = 17645,1476 = 17645,1476
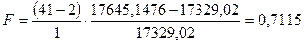
а). На уровне доверия  F=0,7115< F=0,7115< , поэтому принимаем гипотезу , поэтому принимаем гипотезу 
б). На уровне доверия  F=0,7115< F=0,7115< , поэтому принимаем гипотезу , поэтому принимаем гипотезу 
2. y=ax:  = 17983,7 = 17983,7

а). На уровне доверия  F=1,473< F=1,473< , поэтому принимаем гипотезу , поэтому принимаем гипотезу 
б), На уровне доверия  F=1,473< F=1,473< , поэтому принимаем гипотезу , поэтому принимаем гипотезу 

Приложение
Сводная таблица оценок  и и  . .
Интервальные оценки
-15,951 -14,042 4,655 6,563

-10,656 -9,527 1,535 2,664

298,159 317,556 674,543 732,728
Список использованной литературы.
1.Кочетков Е.С. Метод наименьших квадратов: Учебное пособие. Москва, издательствр МАИ, 1993г.
2.М.В.Болдин, Е.Р. Горяинова, А.Р. Панков, С.С Тарасова. Теория вероятностей и математическая статистика: лабораторные работы. Москва, издательство МАИ, 1992г.
3.Кибзун А.И., Горяинова Е.Р., Наумов А.В. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами. Учебное пособие, 2-е издание, исправленное и дополненное. Москва, ФИЗМАТЛИТ, 2005г.
|