Министерство общего и профессионального образования
Московский Авиационный институт (государственный технический университет) «МАИ»
ОТЧЕТ
О НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЕ
Курсовой проект по теории вероятностей и математической статистике
по теме
«Прогнозирование функций по методу наименьших квадратов»
Москва 2009
Реферат
В отчете содержится: 24 формулы, 10 рисунков.
Ключевые слова: тренд прогноза, логнормальный закон, шум, критерий χ2
-Пирсона, проверка гипотез, оценки расхождения.
Целью данной работы было исследование точности прогнозирования случайного процесса с использованием метода наименьших квадратов. Для этого проводился машинный эксперимент с использованием программы Mathcad 14. Основой для построения случайной функции являлась линейная функция, на которую был наложен случайный шум, распределенный по логнормальному закону с параметрами М[шума]=0 (математическое ожидание шума) и D[шума]=D (дисперсия шума). После чего полученная случайная функция аппроксимировалась линейным трендом, а также исследовалось расхождение между трендом и прогнозом с последующей оценкой близости распределения расхождений наблюдений и распределения сгенерированного шума по критерию χ2
-Пирсона.
Определения и формулы
Математическим ожиданием P(ξ=xi
)
дискретной случайной величины ξ
называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е:
 , (1) , (1)
где хi
– значение случайной величины, pi
– вероятность этого значения, n
– общее число значений.
Математическим ожиданием P(ξ=xi
)
непрерывной случайной величины ξ
с плотностью распределения φ(x)
называется число, определяемое равенством:
 , (2) , (2)
где φ(x)
– плотность распределения случайной величины.
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
 (3) (3)
Для непрерывной случайной величины формула (3) будет представлена в виде:
 (4) (4)
Среднее квадратичное отклонение(СКО) – это статистическая величина, описывающая разброс значений изучаемой величины вокруг ее ожидаемого значения:
 (5) (5)
В математической статистике оперируют оценками числовых характеристик, которые ищутся по случайной выборке. В отличие от самих параметров, оценки содержат элемент случайности. К оценкам параметров предъявляют определенные требования:
а) состоятельность – оценка, соответствующая этому требованию, с увеличением объема выборки сходится по вероятности к самому параметру;
б) несмещенность – математическое ожидание такой оценки равно оцениваемому параметру;
в) эффективность – дисперсия эффективной оценки минимальна.
Оценка математического ожидания ищется по формуле:
 , (6) , (6)
где n – объем случайной выборки. Оценка, вычисленная по формуле (6), называется так же статистическим средним.
Оценка дисперсии вычисляется по формуле:
 , (7) , (7)
где m – оценка математического ожидания случайной величины.
Оценка С.К.О. вычисляется по формуле:
 , (8) , (8)
т.е. корень квадратный из оценки дисперсии.
При генерации шума мы используем два закона: нормальное и логнормальное распределение.
Нормальный закон:
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности:
 (9) (9)
Функция распределения F(x) в рассматриваемом случае принимает вид:
 (10) (10)
График 1 – распределение плотности вероятности нормального закона:

Рисунок 1. Плотность вероятности нормального закона
Говорят, что случайная величина X имеет логнормальное распределение с параметрами μ, σ, если X = exp(Y), где Y имеет нормальное распределение с параметрами μ, σ. Случайная величина с логнормальным распределением является непрерывной, и принимает только положительные значения. Графики плотности (привязан к левой вертикальной оси ординат) и функции (привязан к правой оси ординат) логнормального распределения с параметрами μ = 0, σ = 0.7 приведен на следующем рисунке 2:

Рисунок 2. Логнормальное распределение
Плотность распределения логнормального закона:
 (11) (11)
Функция распределения:
 (12) (12)
Для определения степени расхождения теоретической кривой и статистических данных пользуются критериями согласия. Наиболее часто для проверки гипотезы о законе распределения используются 2 критерия: критерий λ-Колмогорова и критерий χ2
-Пирсона.
Расчетное значение для критерия χ2
-Пирсона вычисляется по формуле:
 , где (13) , где (13)
 – (14) – (14)
вероятность попадания в интервал разбиения с номером i
, mi
– число значений функции в интервале разбиения, m, σ
– математическое ожидание и с.к.о. случайной величины X
, Φ*
– интеграл вероятностей.
Чтобы определить функциональную зависимость между величинами по результатам наблюдений, используем метод наименьших квадратов (МНК):
Пусть из опыта получены точки:
x1, y1,
xn, yn
Требуется найти уравнение прямой y=ax+b (15), наилучшим образом согласующейся с опытными точками. Пусть мы нашли такую прямую. Обозначим через δi
расстояние опытной точки от этой прямой (измеренное параллельно оси y).
Из уравнения (15) следует, что:
 (16) (16)
Чем меньше числа по абсолютной величине, тем лучше подобрана прямая (15). В качестве характеристики точности подбора прямой (15) можно принять сумму квадратов:
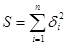 (17) (17)
Покажем, как можно подобрать прямую (15) так, чтобы сумма квадратов S была минимальной. Из уравнений (16) и (17) получаем:
 (18) (18)
Условия минимума S будут равны для линейной функции:
 (19) (19)
 (20) (20)
Уравнения (19) и (20) можно записать в таком виде:
 (21) (21)
 (22) (22)
По уравнениям (21) и (22) легко найти a и b по опытным значениям xi
и yi
. Прямая (15), определяемая уравнениями (21) и (22), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (21) и (22), из которых определяется прямая (15), называются нормальными уравнениями.
В качестве тренда процесса был выбран линейный тренд вида
Y=at+b
, (23)
где а
=1, b
=2. Тренд процесса показан на рисунке 3.
  
Рисунок 3. График тренда
График прямой с учетом сгенерированного шума по логнормальному закону выглядит так:.
  
Рисунок 4. График прямой с учетом шума.
Наша задача в курсовом проекте заключается в определении насколько сильно шум влияет на прогнозирование. Для этого мы определяем расхождения между трендом и прогнозом и оцениваем степень расхождения из-за шума по критерию Пирсона
1. Построение прямой аппроксимирующей свойства тренда с помощью МНК
Наша ошибка сгенерирована по логнормальному закону с математическим ожиданием равным 0 и дисперсией равной 1. Гистограмма распределения шума представлена на рисунке 5.
 
Рисунок 5. (Гистограмма распределения значений шума по интервалам).
С помощью формул (21) и (22) вычислим коэффициенты линейного уравнения тренда с учетом шума с помощью метода МНК:


По найденным коэффициентам строим график прямой, которая аппроксимирует основные свойства линейного тренда. График показан на рисунке 6:
 
Рисунок 6. (Прямая, построенная по методу наименьших квадратов).
2. Прогнозирование дальнейшего продвижения тренда
Наша задача состоит в том, чтобы спрогнозировать дальнейшее поведение уравнения тренда и определить расхождения с спрогнозированными значениями.
Для этого увеличиваем участок наблюдения за линейным трендом без шума до τ =2t=50
График расхождения исходного тренда и аппроксимированного тренда по МНК виден на рисунке 7. (Yτ
– исходный тренд; Zτ
– аппроксимированный тренд по МНК)
 
Рисунок 7 (На рисунке показаны тренд и аппроксимирующая его свойства прямая, построенная по методу наименьших квадратов).
Расхождения вычислены на удаленно отрезке(τ=50):
Δ= Zτ
- Yτ
=0.864
Проведем серию из 25 экспериментов по вычислению расхождений Δ по модулю:
| N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| Δ |
0.661 |
0.673 |
0.756 |
2.366 |
0.488 |
3.569 |
0.864 |
5.651 |
2.328 |
0.851 |
1.259 |
1.718 |
0.618 |
| N |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
| Δ |
3.765 |
0.502 |
3.762 |
1.369 |
2.185 |
0.494 |
1.851 |
0.067 |
2.012 |
4.429 |
3.441 |
0.601 |
Рассчитаем среднее значение Δ и среднеквадратичное отклонение по формулам (6) и (8):
Δср=1.851; σ=1.484
График на рисунке 8 отображает расхождения между исходной функцией и прямыми, полученными в результате аппроксимации по МНК. Синим цветом показаны полученные прямые, красным - исходная функция.
 
Рисунок 8. (На рисунке показаны тренд и несколько прямых, построенных по методу наименьших квадратов и аппроксимирующих свойства тренда).
3. Анализ результатов эксперимента
Полученные значения расхождений Δ представим в виде гистограммы и эмпирической функции по интервалам на рисунке 9:
 

Рисунок 9. (На рисунке представлены гистограмма распределения значений Δ по интервалам, а так же график функции распределения Δ).
Из рисунков видно, что закон Δ больше всего похож на логнормальный, поэтому для сравнения оценки расхождения распределения сгенерируем выборку объемом в 25 (а так же выборки объемом 100, 500 и 1500) по логнормальному закону с математическим ожиданием 0 и дисперсией 1 и вычислим параметры.
Сгенерированная выборка:
| N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| xL |
3.532 |
0.494 |
1.002 |
3.027 |
2.441 |
0.055 |
0.116 |
1.229 |
0.54 |
0.302 |
1.104 |
2.161 |
1.358 |
| N |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
| xL |
1.011 |
0.466 |
0.664 |
0.51 |
0.876 |
2.768 |
1.198 |
1.671 |
2.095 |
0.984 |
1.322 |
1.176 |
Оценки математического ожидания, дисперсии и СКО рассчитаем по формулам:
  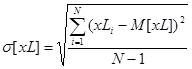 (24) (24)
M[xL]=1.284; D[xL]=0.848; σ[xL]=0.921
На рисунке 10 показана гистограмма и эмпирическая функция по сгенерированной выборке:
  
Рисунок 10. (На рисунке показанная функций распределения, а так же гистограмма распределения значений по интервалам для случайной величины, распределенной по логнормальному закону распределения с выборкой 25).
4. Проверка близости по критерию χ2 Пирсона закона распределения расхождений наблюдений и сгенерированного шума
Проверим насколько расходятся значения при прогнозе и по тренду. Для этого определяются интервалы разбиения расхождений прогноза и вычисление вероятностей попасть в интервал по логнормальному закону с математическим ожиданием равным 0 и дисперсией 1 по формуле (9).
Далее посчитаем сумму квадратов расхождения между частотами и вероятностью попасть в интервал логнормального закона:
 (25) (25)
На основе суммы квадратов расхождения Δрасх можно посчитать расчетное значение критерия согласия Пирсона:
 (26) (26)
На полигоне частот (рисунок 11) показаны значения частоты распределения чисел по интервалам и вероятностей попадания в эти интервалы.
Теоретическое значение критического значения критерия Пирсона при уровне значимости α=0.1 и числом степеней свободы r=m-1 рассчитаем по формуле (11).


Рисунок 11.
(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500 и 1500. Случайная величина распределена по логнормальному закону распределения).
Ставится гипотеза: H0
– расхождение между прогнозом и трендом распределено по логнормальному закону
| Количество экспериментов |
Критическое значение χ² |
Эмпирическое значение χ² |
Решение |
| 25 |
21.064 |
26.135 |
Гипотеза H0
отвергается |
| 100 |
21.064 |
65.549 |
Гипотеза H0
отвергается |
| 500 |
21.064 |
102.753 |
Гипотеза H0
отвергается |
| 1500 |
21.064 |
241.778 |
Гипотеза H0
отвергается |

Рисунок 12.
(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500, 1500 и 10000. Случайная величина распределена по нормальному закону распределения, для проверки взято теоретическое распределение с параметрами mx
=0 и Dx
=1).
Поставим гипотезу: H0
– расхождение между прогнозом и трендом распределено по нормальному закону распределения (с параметрами mx
=0 и Dx
=1).
Количество
экспериментов
|
Критическое значение χ² |
Эмпирическое значение χ² |
Решение |
| 25 |
21.064 |
14.865 |
Гипотеза H0
принимается |
| 100 |
21.064 |
10.266 |
Гипотеза H0
принимается |
| 500 |
21.064 |
9.161 |
Гипотеза H0
принимается |
| 1500 |
21.064 |
32.575 |
Гипотеза H0
отвергается |
| 10000 |
21.064 |
114.286 |
Гипотеза H0
отвергается |
Отвержение гипотезы H0
о распределении случайной величины по нормальному закону при выборках 1500 и 10000 с параметрами mx
=0 и Dx
=1 свидетельствует об изменении параметров закона распределения (т.к. нормальный закон устойчив к линейным преобразованиям и сам закон не меняется), что является следствием линейных преобразований. Используем для проверки гипотезы о законе распределения с помощью критерия Пирсона теоретический закон распределения с дисперсией, равной оценке дисперсии отклонения прогноза от тренда, вычисленной по методу моментов.


Рисунок 13.
(На рисунке показано расхождения между частотой попадания случайной величины в интервал и функцией распределения для попадания в этот интервал для выборок 25, 100, 500, 1500 и 10000. Случайная величина распределена по нормальному закону распределения, для проверки взято теоретическое распределение с параметрами mx
=0 и Dx
= DΔ
(DΔ
=1.343; 1.149; 1,235; 1.158; 1.141)).
Поставим новую гипотезу: H0
– расхождение между прогнозом и трендом распределено по нормальному закону распределения (с параметрами mx
=0 и Dx
=DΔ
).
Количество
экспериментов
|
Критическое значение χ² |
Эмпирическое значение χ² |
Решение |
| 25 |
21.064 |
12.251 |
Гипотеза H0
принимается |
| 100 |
21.064 |
11.616 |
Гипотеза H0
принимается |
| 500 |
21.064 |
11.503 |
Гипотеза H0
принимается |
| 1500 |
21.064 |
14.31 |
Гипотеза H0
принимается |
| 10000 |
21.064 |
11.275 |
Гипотеза H0
принимается |
Отклонение тренда от прогноза при шуме, распределенном по нормальному закону распределении, так же подчиняется нормальному закону распределения, что было подтверждено экспериментально.
а) на основании проведенных экспериментов и анализа полученных данных можно сделать вывод, подтверждающий, что логнормальное распределение является неустойчивым к линейным преобразованиям, причем с ростом числа наблюдений расхождение будет существенно возрастать;
б) при аппроксимации линейного тренда, к которому был добавлен шум, распределенный по логнормальному закону распределение все прямые, построенные по методу наименьших квадратов, всегда проходили выше прямой тренда. Это является следствием влияния ошибки наблюдений, которая была положительной величиной и говорит о том, что эффективность метода наименьших квадратов при аппроксимации тренда с положительной ошибкой наблюдений ниже, чем при аппроксимации тренда с ошибкой наблюдения, имеющее разные знаки;
в) при аппроксимации линейного тренда, к которому был добавлен шум, распределенный по нормальному закону, распределение отклонения прогноза от тренда так же подчинено нормальному закону распределения, в силу устойчивости последнего к линейным преобразованиям, но, из-за преобразований меняется его дисперсия (в нашем случае увеличивается в среднем на 12%), что было экспериментально подтверждено с использованием критерия Пирсона.
1. В.В. Бомас, В.С. Булыгин «Элементы теории Марковских процессов и ее технические приложения».
2. Феллер «Введение в теорию вероятностей и ее приложения»
3. Е.С. Вентцель «Теория вероятностей».
|