Контрольная работа: Кручение упругопластического стержня
|
Название: Кручение упругопластического стержня Раздел: Рефераты по информатике Тип: контрольная работа | ||||||||||||||||||||||||||||||||||||||||||
Санкт-Петербургский государственный политехнический университет КУРСОВАЯ РАБОТА Дисциплина: Математические и численные методы механики сплошных сред Тема: Кручение упругопластического стержня Санкт-Петербург 2008 2. Математическая корректность. 5 В данной работе исследуется задача о кручении упругопластического стержня. Рассмотрим очень длинный стержень. Выделим участок длины  Рис.1 Стержень длины h
Сделаем следующие предположения: 1. стержень сделан из изотропного материала; 2. на стержень не действуют объемные силы; 3. боковая поверхность свободна от нагружений; 4. 5. 6. 7. Из второго условия следует, что уравнение равновесия запишется в виде:
Тогда допустимые поля напряжений принадлежат множеству
Последние два условия задают поворот точек верхнего сечения вокруг оси В соответствии с принципом Хаара-Кармана поле
Можно показать, что решение этой задачи таково, что все компоненты
Введем функцию тока
Тогда уравнение (1.4) автоматически выполнено. Уравнения
С другой стороны, Следовательно, Рассмотрим условие пластичности Мизеса:
В данном примере,
В итоге принцип Хаара-Кармана приводит к следующей вариационной задаче: З1
: Найти
где
Если ввести билинейную форму
или в форме вариационного неравенства: 2. Математическая корректность Теперь покажем, что задача З1 математически корректна. Задача называется математически корректной, если выполнены три условия: 1) ее решение существует (условие существования); 2) решение единственно (условие единственности); 3) решение задачи непрерывно зависит от данных задачи (условие устойчивости). Проверим выполнение всех трех условий. Существование решения обеспечивается теоремой вариационного исчисления о том, что полунепрерывный выпуклый функционал достигает своей точной нижней грани на непустом, выпуклом, замкнутом подмножестве рефлексивного банахова пространства.
Подмножество Покажем, что
Пусть Тогда Следовательно, т.е. функционал является непрерывным. Покажем выпуклость функционала, используя его запись в общем виде.
Таким образом, все условия указанной выше теоремы выполнены, и, следовательно, задача З1 имеет решение. Утверждение 1.
Билинейная форма Доказательство:
Утверждение 2. Решение задачи З1 единственно. Доказательство: Будем доказывать это утверждение от противного. Пусть существуют различные Тогда, из (1.11) выполнено:
Подставим в (2.2.1) Получим
Умножим (2.2.4) на -1: Отсюда,
Форма Окончательно, Решение Перепишем неравенство (2.3.1) как Неравенство (2.3.2) выполняется для Оценим правую часть неравенства (2.3.3) сверху:
Левую часть (2.3.3) оценим снизу:
Тогда
Рассмотрим семейство конечномерных пространств Будем строить Построим триангуляцию области Для каждого узла триангуляции 1. 2. 3. Составим пространство Теперь необходимо аппроксимировать множество Пусть Покажем, что множество 1) От противного:
Пусть Но, по свойству предельной плотности
Отсюда, по лемме о сохранении строгих неравенств 2)
Запишем задачу З1
: найти Наряду с ней сформулируем задачу З2 : найти При сделанных предположениях относительно Для решения задачи З2 будем использовать метод штрафа. Исходная вариационная задача: Построим вспомогательный функционал
Тогда вместо решения задачи (4.1) можем решать задачу Кроме того, Производная Гато функции Тогда задача
Можно показать, что Следовательно, решение вариационной задачи Замечания по реализации: Неизвестную функцию решения
Тогда задача минимизации функционала (4.2) превратится в задачу многомерной минимизации по
Алгоритм для нахождения минимума функционала (4.2) реализован в среде Matlab. Были проведены расчеты для различных форм сечений стержня (области В случае если сечение стержня – круг, то известно аналитическое решение задачи.
1) На рис. 2-5 продемонстрированы численные решения задачи при разных разбиениях
Рис.2 Число узлов = 29
Рис.3 Число узлов = 146
Рис.4 Число узлов = 270
Рис.5 Число узлов = 549 Для оценки погрешности решения введем величину Здесь
В таблице 1 приведены результаты сравнения численного и точного решения.
Таблица 1 Результаты сравнения (1). 2) На рис. 6-9 продемонстрированы численные решения задачи при разных разбиениях
Рис.6 Число узлов = 29
Рис.7 Число узлов = 146
Рис.8 Число узлов = 270
Рис.9 Число узлов = 549 Как и в первом примере, вычислена относительная ошибка, см. Таблицу 2.
Таблица 2 Результаты сравнения (2). 3) На Рис.10-11 изображены численные решения задачи для стержня с квадратным сечением, Рис.10 Число узлов = 27
Рис.11 Число узлов = 177 4) На Рис.12 изображено численное решение задачи для стержня с треугольным сечением,
Рис.12 Число узлов = 144 В ходе выполнения данной работы была изучена задача о кручении упругопластического стержня. Показано, что решение задачи существует и единственно. Предложен метод численного решения поставленной задачи, основанный на применении конечноэлементного подхода для перехода от бесконечномерной задачи к конечномерной, а также на применении метода штрафа для минимизации целевого функционала. Проведены различные численные эксперименты; для случая, когда известно аналитическое решение задачи, вычислена относительная ошибка численного решения по сравнению с точным.
|

 (2.1.1)
(2.1.1) 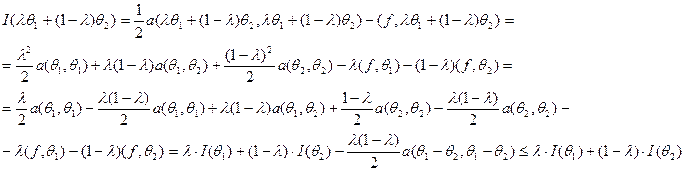
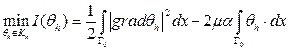 (4.1)
(4.1)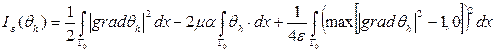 (4.2)
(4.2)

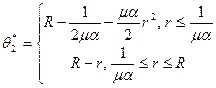




 , характеризующую относительную погрешность.
, характеризующую относительную погрешность. .
.





