Определение момента инерции в машине Атвуда
Приборы и принадлежности:
машина Атвуда, набор грузов, секундомер, масштабная линейка.
Цель работы:
изучение вращательного и поступательного движений на машине Атвуда, определение момента инерции блока и момента сил трения в оси блока.
Описание установки и исследуемые закономерности
 Машина Атвуда является настольным прибором, ее изображение приведено на рис. 3.1. На вертикальной стойке 1 основания 2 расположены три кронштейна: нижний 3, средний 4 и верхний 5. На верхнем кронштейне 5 крепится блок с узлом подшипников качения, через который переброшена нить с грузом 6. На верхнем кронштейне находится электромагнит 7, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии. Машина Атвуда является настольным прибором, ее изображение приведено на рис. 3.1. На вертикальной стойке 1 основания 2 расположены три кронштейна: нижний 3, средний 4 и верхний 5. На верхнем кронштейне 5 крепится блок с узлом подшипников качения, через который переброшена нить с грузом 6. На верхнем кронштейне находится электромагнит 7, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии.
На среднем кронштейне 4 крепится фотодатчик 8, выдающий электрический сигнал по окончанию счета времени равноускоренного движения грузов. На среднем кронштейне есть риска, совпадающая с оптической осью фотодатчика. Нижний кронштейн представляет собой площадку с резиновым амортизатором, о который ударяется груз при остановке. На вертикальной стойке 1 укреплена миллиметровая линейка 9, по которой определяют начальное и конечное положение грузов, т.е. пройденный путь.
Начальное положение определяют визуально по нижнему краю груза, конечное положение – по риске среднего кронштейна. Секундомер 10 выполнен как самостоятельный прибор с цифровой индикацией времени.
Машина Атвуда предназначена для изучения законов поступательного и вращательного движений. Принцип работы установки основан на том, что, когда на концах нити подвешены грузы различной массы, система начинает двигаться равноускоренно. В комплект грузов входит несколько перегрузов, что позволяет исследовать движения с различными ускорениями.
На каждый груз действует две силы – сила тяжести и сила натяжения нити, под действием которых грузы движутся. Полагая, что нить невесома и нерастяжима, получим, что ускорения обоих грузов будут постоянны, одинаковы по значению и противоположны по направлению.
На основании второго закона Ньютона для первого груза с перегрузом и второго груза можно записать
 ; (1) ; (1)
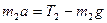 , (2) , (2)
где m1
и m2
– массы 1-го и 2-го грузов; 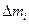 - масса перегруза, находившегося на 1-м грузе; Т1
и Т2
– силы натяжения нити, действующие на 1-й и 2-й грузы; a
– ускорение грузов. Вращение блока описывается уравнением - масса перегруза, находившегося на 1-м грузе; Т1
и Т2
– силы натяжения нити, действующие на 1-й и 2-й грузы; a
– ускорение грузов. Вращение блока описывается уравнением
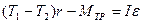 ; (3) ; (3)
где r
– радиус блока; 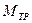 - момент сил трения в оси блока; I
– момент инерции блока; - момент сил трения в оси блока; I
– момент инерции блока; 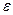 - угловое ускорение блока. Из этих уравнений можно получить: - угловое ускорение блока. Из этих уравнений можно получить:
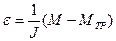 ; (4) ; (4)
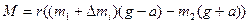 ; (5) ; (5)
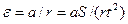 , (6) , (6)
где S– пройденный грузом за время tпуть.
Целью выполнения работы является определение момента инерции блока и момента сил трения в блоке. Для этого экспериментально исследуется зависимость М от ε. Различные значения М реализуются с помощью набора перегрузов массой  и определяются по формуле. Значения ε рассчитываются по формуле. Величины I
и Мтр
определяются по формулам линейной регрессии (методом наименьших квадратов). и определяются по формуле. Значения ε рассчитываются по формуле. Величины I
и Мтр
определяются по формулам линейной регрессии (методом наименьших квадратов).
Результаты наблюдений
Таблица №1
| t, c |
| Перегруз 1,3 г |
| 1 |
2,61 |
| 2 |
2,761 |
| 3 |
2,77 |
| Перегруз 2,2 г |
| 1 |
2,226 |
| 2 |
2,242 |
| 3 |
2,229 |
| Перегруз 2,6 г |
| 1 |
1,95 |
| 2 |
1,968 |
| 3 |
1,937 |
| Перегруз 3,9 г |
| 1 |
1,597 |
| 2 |
1,525 |
| 3 |
1,54 |
| Перегруз 4,8 г |
| 1 |
1,445 |
| 2 |
1,444 |
| 3 |
1,467 |
| Перегруз 5,8 г |
| 1 |
1,285 |
| 2 |
1,299 |
| 3 |
1,283 |
Значение масс 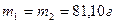
Значение с прибора 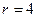 см см
Расчеты:
Для определения I
и 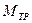 методом наименьших квадратов по уравнению (4) необходимо рассчитать: методом наименьших квадратов по уравнению (4) необходимо рассчитать:
- 
- 
Для каждого случая.
Таблица №2
t,
сек
|
 , ,
кг
|
M,
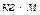
|
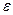 , ,

|
a,
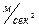
|
| 2,61 |
0,0013 |
0,00016 |
2,569 |
0,103 |
| 2,761 |
0,0013 |
0,000091 |
2,296 |
0,092 |
| 2,77 |
0,0013 |
0,000087 |
2,281 |
0,091 |
| 2,226 |
0,0022 |
0,000067 |
3,532 |
0,141 |
| 2,242 |
0,0022 |
0,000053 |
3,482 |
0,139 |
| 2,229 |
0,0022 |
0,000064 |
3,522 |
0,141 |
| 1,95 |
0,0026 |
0,00019 |
4,602 |
0,184 |
| 1,968 |
0,0026 |
0,00017 |
4,518 |
0,181 |
| 1,937 |
0,0026 |
0,00021 |
4,664 |
0,187 |
| 1,597 |
0,0039 |
0,00029 |
6,862 |
0,274 |
| 1,525 |
0,0039 |
0,00047 |
7,525 |
0,301 |
| 1,54 |
0,0039 |
0,00043 |
7,379 |
0,295 |
| 1,445 |
0,0048 |
0,00036 |
8,381 |
0,335 |
| 1,444 |
0,0048 |
0,00036 |
8,393 |
0,336 |
| 1,467 |
0,0048 |
0,00029 |
8,132 |
0,325 |
| 1,285 |
0,0058 |
0,00058 |
10,598 |
0,424 |
| 1,299 |
0,0058 |
0,00051 |
10,371 |
0,415 |
| 1,283 |
0,0058 |
0,00058 |
10,631 |
0,425 |
Из сопоставлений линейной зависимости 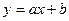 и уравнения (3) получим и уравнения (3) получим
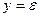 ; ; 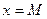 ; ; 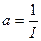 ; ; 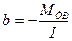 (7) (7)
Заменив в этих формулах XK
на МК
, а YK
на 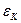 , вычислим параметры линейной зависимости по формулам МНК. , вычислим параметры линейной зависимости по формулам МНК.
Среднее значение X(MK
), Y(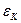 ): ):
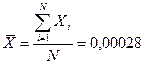 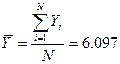
Вычисляем среднее значение коэффициентов а и b:
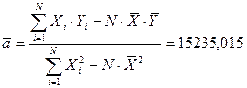 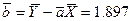
Из соотношения (7) получим:
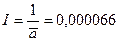
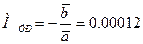
Окончательный результат:
Момент сил трения в оси блока = 0,00012
Момент инерции блока = 0,000066
Вывод:
в ходе работы были изучены вращательное и поступательное движения на машине Атвуда, определен момента инерции блока и момента сил трения в оси блокаи
|