Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Вятский государственный гуманитарный университет»
Физико-математический факультет
Кафедра дидактики физики и математики
Выпускная квалификационная работа
Компетентностно-ориентированные задачи в процессе обучения математике учащихся основной школы
Выполнила студентка V курса
физико-математического факультета
(специальность 050201.65 Математика)
Русских Анна Витальевна
Научный руководитель:
кандидат педагогических наук,
старший преподаватель кафедры
дидактики физики и математики
Малых Елена Владимировна
Рецензент:
кандидат педагогических наук,
старший преподаватель кафедры
дидактики физики и математики
Горев Павел Михайлович
Работа допущена к защите в ГАК
«___» _________2008 г. Зам. зав. кафедрой ________ М. В. Крутихина
«___» _________2008 г. Декан факультета ___________ Е. В. Кантор
Киров 2008
Оглавление
Введение
1. Международное исследование образовательных достижений учащихся PISA (Programme for International Student Assessment) как измеритель качества математической подготовки школьников
1.1.Цели и задачи исследования PISA
1.2. Понятие математической грамотности в исследованиях PISA
1.3.Основные результаты изучения математической грамотности в исследованиях PISA
Выводы по первому параграфу
2. Компетентностный подход как средство повышения качества математической грамотности учащихся основной школы
2.1. Понятие компетентностного подхода и сравнение его с традиционным
2.2. Ключевые компетентности
2.3. Формирование ключевых компетентностей через учебные математические задачи
Выводы по второму параграфу
3. Компетентностно-ориентированные математические задачи
3.1. Содержание компетентностно-ориентированных математических задач
3.2. Три уровня компетентностно-ориентированных задач
Выводы по третьему параграфу
4. Методические рекомендации использования компетентностно-ориентированных математических задач
4.1. Содержание учебника математики как среда для составления компетентностно-ориентированных задач
4.2. Место компетентностно-ориентированных математических задач в процессе изучения математики.
4.2.1. Компетентностно-ориентированные задачи на уроках изучения нового материала
4.2.2. Компетентностно-ориентированные задачи на уроках комплексного применения знаний
4.2.3. Компетентностно-ориентированные задачи в качестве домашнего задания
Выводы по четвертому параграфу
5. Опытное преподавание в 9 классе
Заключение
Список библиографии
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Введение
Современное общество меняет взгляд на содержание математического образования. Основное внимание направлено на развитие способности учащихся применять полученные в школе знания и умения в жизненных ситуациях.
В международных исследованиях PISA (Programme for International Student Assessment) математическая грамотность определяется как «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину». В исследованиях проверяется способность 15-летних учащихся использовать математические знания в ситуациях близких к реальным, связанных с разнообразными аспектами окружающей действительности: жизни школы, общества, личной жизни учащихся и т.д.
Невысокие результаты наших школьников во всех трех циклах исследования (2000 г., 2003 г., 2006 г.) вызвали широкую дискуссию в обществе о качестве российского образования, приоритетах в содержании математического образования.
Многие ученые и школьные учителя видят выход из создавшейся ситуации в реализации компетентностного подхода при обучении математике учащихся основной школы. Данный подход не отрицает значения знаний, но акцентирует внимание на способности использовать полученные знания в жизни. При таком подходе цели образования описываются в терминах, отражающих новые возможности обучаемых, рост их личного потенциала.
Важнейшим видом учебной деятельности при обучении школьников математике является решение задач. Поэтому целесообразно формировать ключевые компетентности через специальные компетентностно-ориентированные задачи, аналогичные задачам для проверки математической грамотности в исследованиях PISA.
Вместе с тем, таких задач в учебниках, учебных пособиях, дидактических материалах немного. Составление же компетентностно-ориентированных задач достаточно трудоемко. Поэтому учителя математики редко используют их на занятиях.
Таким образом, имеем противоречие между необходимостью обучения решению компетентностно-ориентированных задач учащихся основной школы и неразработанностью методики их использования в процессе обучения математике. Разрешение противоречия определяет актуальность выпускной квалификационной работы.
Объектом исследования
является процесс обучения математике учащихся основной школы.
Предметом исследования
служат компетентностно-ориентированные задачи в этом процессе.
Цель работы
состоит в выявлении роли компетентностного подхода в процессе обучения математике учащихся основной школы и разработке методических рекомендаций по использованию компетентностно- ориентированных задач.
В основу работы положена гипотеза
: если на уроках математики и внеклассных занятиях в основной школе систематически использовать компетентностно-ориентированные задачи в соответствии с разработанными методическими рекомендациями, то повысится математическая грамотность учащихся.
Для достижения поставленной цели и проверки сформулированной гипотезы потребовалось решить следующие задачи
:
1. Рассмотреть понятие математической грамотности с точки зрения разработчиков международных исследований PISA.
2. Рассмотреть понятие компетентностного подхода в научной и научно-методической литературе, выявить его роль в процессе обучения математике учащихся основной школы.
3. Рассмотреть содержательный аспект и определить уровни компетентностно-ориентированных задач.
4. Разработать методические рекомендации по использованию компетентностно-ориентированных задач.
5. Изучить опыт работы учителей математики по использованию компетентностно-ориентированных задач на уроках.
6. Проверить эффективность методических рекомендаций путем опытного преподавания.
Для решения задач использованы следующие методы
:
1. Изучение методической литературы по данной теме;
2. Изучение опыта работы преподавателей;
3. Анализ упражнений из школьных учебников по математике;
4. Анализ международных исследований в области математической грамотности;
5. Опытное преподавание.
Теоретическая значимость
работы состоит в разработке методических рекомендаций для составления и использования компетентностно-ориентированных задач на уроках математики в основной школе.
Практическая значимость
работы состоит в возможности использования студентами и преподавателями разработанных материалов при подготовке к урокам и факультативным занятиям по математике.
Работа состоит из введения, пяти параграфов, заключения, библиографического списка и 5 приложений.
1 Международное исследование образовательных достижений учащихся
PISA
(Programme for International Student Assessment) как измеритель качества математической подготовки школьников
1.1 Цели и задачи исследования
PISA
В последнее время меняется взгляд на то, какой должна быть подготовка выпускника основной школы. Наряду с получением предметных знаний и умений, школа должна вырабатывать умения использовать их в разнообразных ситуациях, близких к реальным [5].
Организация Экономического Сотрудничества и Развития (OECD) начала работу по Международной Программе оценки знаний и умений учащихся (PISA), основная цель которой – получение надежных сведений о результатах обучения в различных странах мира, сравнимых на международном уровне.
Исследование PISA проводится трехлетними циклами (первый цикл -1997-2000 гг., второй цикл -2000-2003 гг., третий цикл - 2003-2006 гг.). Дополнительно к оценке учебных достижений изучается отношение учащихся к обучению. По мнению разработчиков, полученная информация позволит странам-участницам принимать обоснованные решения в области образования. Особый интерес вызывает возможность определить состояние тех знаний и умений, которые могут быть полезны ребятам в будущем, а так же умения самостоятельно приобретать знания, необходимые для успешной адаптации в современном мире.
Исследование проводится среди учащихся 15-летнего возраста. Ключевой вопрос исследования – «Обладают ли учащиеся 15-летнего возраста, получившие общее обязательное образование, знаниями и умениями, необходимыми для полноценного функционирования в обществе?» (15, с. 5). Исследование направлено не на определение уровня освоения школьных программ, а на оценку способности учащихся применять полученные знания и умения в жизненных ситуациях.
Такой выбор объясняется тем, что во многих странах к этому возрасту завершается обязательное обучение в школе и программы обучения в разных странах имеют много общего. Именно на этом этапе образования важно определить состояние тех знаний и умений, которые могут быть полезны школьникам в будущем, а также способности самостоятельно приобретать знания, необходимые для успешной адаптации в современном мире.
Проверке овладения конкретным содержанием учебных дисциплин не уделяется много времени. Основное время отводится изучению состояния более широких знаний и умений, необходимых во взрослой жизни и приобретенных при изучении школьных предметов, а также оценке межпредметной компетентности учащихся (использованию знаний, полученных в рамках изучения различных предметов или из других источников информации, для решения поставленной задачи).
В каждом цикле исследования оценивается функциональная грамотность учащихся в области чтения, математики, естествознания. В 2000 году приоритетной областью исследования была грамотность чтения, в 2006 – естественнонаучной грамотности, в 2003 году - математическая грамотность.
1.2 Понятие математической грамотности в исследованиях PISA
В исследованиях PISA-2003проверка математической подготовки учащихся основана на понятии «математическая грамотность», которое определяется как «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину» (15, с.7).
Содержание этого понятия уточняется следующим образом: «под математической грамотностью понимается способность учащихся:
· распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены средствами математики;
· формулировать эти проблемы на языке математики;
· решать эти проблемы, используя математические знания и методы;
· анализировать использованные методы решения;
· интерпретировать полученные результаты с учетом поставленной проблемы;
· формулировать и записывать окончательные результаты решения поставленной проблемы» [15, с. 7].
В исследованиях PISA-2000, PISA-2003 и PISA-2006 основное внимание было уделено проверке способностей учащихся использовать математические знания в ситуациях близких к реальным, связанных с разнообразными аспектами окружающей действительности: жизни школы, общества, личной жизни учащихся и т.д.
Для решения поставленных проблем учащимся необходимо иметь значительный объем математических знаний и умений, которые обычно формируются в школе. В исследовании не ставится цель проверить каждое из выделенных предметных знаний и умений в отдельности. В большинстве ситуаций требуется использовать знания и умения из разных тем и разделов не только курса математики, но и других школьных предметов, например, физики, биологии, химии. Необходимо также такое важнейшее общеучебное умение, как умение внимательно прочитать некоторый связный текст, выделить в приведенной в нем информации только те факты и данные, которые необходимы для получения ответа на поставленный вопрос.
В соответствии с замыслом авторов концепции исследования каждое задание соответствует одной из четырех содержательных областей:
1. Пространство и форма
— это вопросы, относящиеся к пространственным и плоским геометрическим формам и отношениям, которые часто встречаются в школьных программах по геометрии разных стран. Они связаны с поиском сходства в различия при анализе фигур и их частей, распознаванием фигур в различных конфигурациях и с разными размерами, а также пониманием свойств объектов и их взаимного расположения.
2. Изменение и отношения
– вопросы, связанные с математическим описанием различных процессов, таких как зависимости между переменными, в том числе функциональные. В большей степени этот материал относится к алгебре. Математические отношения, рассматриваемые в заданиях, могут выражаться уравнениями или неравенствами, но используются также и отношения более общей природы (например, эквивалентность, делимость, включение). Отношения задаются разными способами, включая символические, алгебраические, графические, табличные и геометрические.
3. Количество
— эта область включает вопросы, связанные с числами. В программах по математике этот материал чаще всего относится к арифметике. При выполнении заданий от учащихся требуется умение выполнять сравнение чисел и величин, распознавать числовые выражения и формулы, использовать числа для представления количественных характеристик реальных объектов (подсчеты и измерения). Кроме того, эта область связана с пониманием разных форм представления чисел и выполнением действий с числами, представленными в разных формах. Важным аспектом в соответствующих задачах являются также рассуждения, связанные с числами и проявляющиеся во владении разными представлениями чисел, а также в понимании смысла операций, устных вычислений и приближенных оценок.
4. Неопределенность
— включает в себя вероятностные и статистические явления и зависимости, которые имеют самое непосредственное отношение к современному информационному обществу. Эти явления и зависимости являются предметом изучения разделов статистики и вероятности.
На международном уровне для грамотного современного человека считаются необходимыми следующие математически знания и умения: пространственные представления; пространственное воображение; свойства пространственных фигур; умение читать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей); знаковые и числовые последовательности; определение периметра и площадей нестандартных фигур; действия с процентами; использование масштаба; использование статистических показателей для характеристики различных реальных явлений и процессов; умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости) и др.
1.3 Основные результаты изучения математической грамотности в исследованиях PISA
Во всех трех циклах PISA российские школьники показали невысокий уровень математической грамотности.
В качестве основной количественной характеристики математической подготовки учащихся конкретной страны используется средний балл, подсчитанный по результатам выполнения математической части работы учащимися этой страны.
Среди стран-участниц исследований PISA Россия в 2000 году занимала21 место из 32 стран, в 2003 году – 29 место из 40, в 2006 году – 34 место из 57.
Результаты международного исследования PISA-2000вызвали широкую дискуссию в обществе о качестве российского математического образования, приоритетах в содержании общего среднего образования, способствовавшую появлению новых направлений исследований, прежде всего, - в области изучения целесообразности и возможности реализации так называемого компетентностного подхода в образовании.
В 2001 году распоряжением Правительства Российской Федерации была принята Концепция модернизации Российского образования до 2010 года. В соответствии с Концепцией общеобразовательная школа призвана формировать «новую систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть современные ключевые компетентности» [16]. Определенные таким образом цели образования ориентируют на компетентностный подход к организации образовательного процесса [22].
Однако, итоги исследований PISA -2003 и PISA -2006 показали, что результаты российских школьников по сравнению со сверстниками других стран (близких к России вPISA -2000), не только не улучшились, но и ухудшились.
В таблице 1 приведены итоги исследований в тех странах, результат которых практически не отличался от результата российских школьников в исследовании PISA-2000.
Таблица 1
Средние результаты пяти стран по математической грамотности
| Страны |
PISA-2000 |
PISA-2003 |
PISA-2006 |
| Венгрия |
488 |
490 |
491 |
| Германия |
490 |
503 |
504 |
| Латвия |
463 |
483 |
486 |
| Польша |
470 |
490 |
495 |
| Россия
|
478
|
468
|
476
|
Из таблицы видно, что результаты всех стран, которые не отличались от результатов России в начале исследования, значительно улучшились в последующем. Чего нельзя сказать о результатах российских школьников. Результаты исследования математической грамотности не только не улучшились, а наоборот ухудшились.
Сравнение результатов России с другими странами показывает отличие приоритетов отечественного математического образования от приоритетов, которые проявились в международных исследованиях. Пятнадцатилетние российские учащиеся в этих исследованиях явно продемонстрировали, что они затрудняются в решении задач, в которых представлены ситуации, близкие к реальным. Это свидельствует о том, что заявленная в школьной программе необходимость прикладной и практической ориентации на практике не реализуется [6].
Школьные учителя объясняют такое положение дел тем, что для реализации компетентностного подхода с целью повышения математической грамотности учащихся недостаточно разработано методическое обеспечение процесса обучения математике в основной школе.
Анализ результатов международных проверок позволил выявить характерные недочеты математической подготовки российских школьников. К ним относятся недостаточное усвоение ряда тем, имеющих широкое практическое применение: отношение чисел, пропорциональные величины, решение задач на проценты, определение периметров и площадей фигур, оценка и прикидка результатов, чтение графиков реальных зависимостей.
Результаты исследований позволяют определить направления совершенствования содержания математического образования в школах России. По мнению Г.С.Ковалевой «прежде всего, уже с начальной школы следует изучать тему «Анализ данных. Вероятность. Статистика», овладение которой способствует адаптации учащихся в обществе. Необходимо уменьшить внимание к формированию аппаратных умений и усилить роль знаний, имеющих важное практическое значение. В курсе математики 5-6 классов следует уделить большое внимание наглядной геометрии и вопросам прикладного характера (оценке и прикидке результатов, анализу количественных данных, представленных в различной форме; процентным расчетам; пропорциональным величинам). В курсе 7-9 классов эти направления должны получить дальнейшее развитие. Необходимо увеличить количество заданий практического содержания, связанных с описанием реальных ситуаций»[7].
Выводы по первому параграфу
В последнее время меняется взгляд на то, какой должна быть подготовка выпускника основной школы по математике.
В международных исследованиях PISAпод математической грамотностью понимается «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину».
На международном уровне для грамотного современного человека считаются необходимыми следующие математически знания и умения: пространственные представления; пространственное воображение; свойства пространственных фигур; умение читать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей); знаковые и числовые последовательности; определение периметра и площадей нестандартных фигур; действия с процентами; использование масштаба; использование статистических показателей для характеристики различных реальных явлений и процессов; умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости) и др.
Во всех трех исследованиях PISA российские школьники показали невысокий уровень математической грамотности.
Итоги международного исследования PISAвызвали широкую дискуссию в обществе о качестве российского математического образования.
В 2001 году распоряжением Правительства Российской Федерации была принята Концепция модернизации Российского образования до 2010 года. В этом документе общеобразовательная школа призвана формировать «новую систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть современные ключевые компетентности». Такие же цели и задачи сформулированы в концепции математического образования.
Определенные таким образом цели образования ориентируют на компетентностный подход к организации образовательного процесса, предполагают смену требований к критериям оценки результатах обучения.
Однако, итоги исследований PISA -2003 и PISA -2006 показали, что результаты российских школьников по сравнению со сверстниками других стран (близких к России вPISA -2000), не только не улучшились, но и ухудшились.
Школьные учителя объясняют такое положение дел тем, что для реализации компетентностного подхода с целью повышения математической грамотности учащихся недостаточно разработано методическое обеспечение процесса обучения математике в основной школе.
2. Компетентностный подход как средство повышения качества математической грамотности учащихся основной школы
2.1 Понятие компетентностного подхода и сравнение его с традиционным
Понятие «компетентностный подход» и «ключевые компетентности» получили распространение сравнительно недавно в связи с дискуссиями о проблемах и путях модернизации российского образования. Обращение к этим понятиям связано со стремлением определить необходимые изменения в образовании, в том числе в школьном, обусловленные изменениями, происходящими в обществе [9].
Разные ученые трактуют это понятие по-разному.
Некоторые ученые [23] дают такое определение: «Компетентностный подход – это подход, акцентирующий внимание на результате образования, причем в качестве результата рассматривается не сумма усвоенной информации, а способность человека действовать в различных проблемных ситуациях».
Компетентностный подход заключается в привитии и развитии у школьников набора ключевых компетентностей, которые определяют его успешную адаптацию в обществе.
О.Е.Лебедев считает, что «
компетентностный подход – это совокупность общих принципов определения целей образования, отбора содержания образования, организации образовательного процесса и оценки образовательных результатов» [11, с.3].
К числу таких принципов он относит: смысл образования, содержание образования, смысл организации образовательного процесса, оценку образовательных результатов.
Смысл образования
заключается в «развитии у обучаемых способности самостоятельно решать проблемы в различных сферах и видах деятельности на основе использования социального опыта, элементом которого является и собственный опыт учащихся» [11, с.3].
Содержание образования
представляет собой «дидактически адаптированный социальный опыт решения познавательных, мировоззренческих, нравственных, политических и иных проблем» [11, с.3].
Смысл организации образовательного процесса
заключается в «создании условий для формирования у обучаемых опыта самостоятельного решения познавательных, коммуникативных, организационных, нравственных и иных проблем, составляющих содержание образования» [11, с.3].
Оценка образовательных результатов
основывается на «анализе уровней образованности, достигнутых учащимися на определенном этапе обучения» [11, с.3].
Многие идеи компетентностного подхода появились в результате изучения ситуации на рынке труда и в результате определения тех требований, которые складываются на рынке труда по отношению к работнику. Поэтому школа должна готовить своих учеников к переменам, развивая у них такие качества, как «мобильность, динамизм, конструктивность, инициативность, умение самостоятельно принимать решения» [8].
Сравним традиционный и компетентностный подходы по следующим принципам: цели обучения, пути формирования ценностных ориентаций, ожидаемый результат, критерии оценки и образовательные программы [11].
Таблица 2
Сравнение традиционного и компетентностного подходов
| Традиционныйподход |
Компетентностныйподход |
| Цели обучения |
Ориентация на сохранение экстенсивного пути развития школы (чем больше знаний приобрел ученик, тем лучше, тем выше уровень его образованности).
Цели образования моделируют результат, который можно описать, ответив на вопрос: что нового узнает ученик в школе?
|
Развитие способности решать проблемы различной сложности на основе имеющихся знаний(не отрицает значения знаний, акцентирует внимание на способности использовать полученные знания.
Цели образования предполагают ответ на вопрос: чему научился ученик за годы обучения в школе?
|
| Пути формирования ценностных ориентаций |
Личностный результат можно достичь за счет приобретения необходимых знаний. |
Основной путь - получение опыта самостоятельного решения проблем.
|
| Ожидаемый результат |
Усвоение сведений, понятий, способность решать типовые задачи, умение действовать по алгоритму и т.д. |
Умение видеть проблему, анализировать данные и ожидаемый результат, умение создавать модель, необходимую для решения проблемы, анализировать ее – важнейший результат обучения. |
| Критерии оценки |
Пятибальная шкала оценок. Одну и ту же оценку можно получить, сделав разные ошибки. |
Расширяется шкала оценок, оценка сопровождается словесными пояснениями, комментариями, рекомендациями. Большое внимание уделяется анализу работ. |
| Образовательные программы |
Программы по предметам разрабатываются независимо друг от друга. Связи между ними представлены в лучшем случае на уровне выделения общих понятий. |
Программа по отдельным предметам должна рассматриваться как элемент образовательной программы школы.
При разработке данных программ нужно их связывать с определенным этапом школьного образования – ступенью школы, классом.
|
Рассмотрев табл.2, можно сделать вывод о том, что компетентностный подход в образовании в большей степени соответствует социальным ожиданиям в сфере образования, и интересам участников образовательного процесса на современном этапе.
По мнению О.Е.Лебедева компетентностный подход обладает значительным потенциалом. Он позволяет:
1. научить учиться (определять цели познавательной деятельности, выбирать необходимые источники информации, выбирать оптимальные способы реализации поставленных целей, оценивать полученные результаты);
2. научить объяснять явления действительности, их сущность, причины, взаимосвязи;
3. научить ориентироваться в ключевых проблемах современной жизни – экологических, политических и др.;
4. научить ориентироваться в мире духовных ценностей, отражающих разные культуры и мировоззрения;
5. научить решать проблемы, связанные с реализацией определенных социальных ролей;
6. научить решать проблемы, общие для различных видов профессии и иной деятельности.
2.2 Ключевые компетентности
С позиции компетентностного подхода основным непосредственным результатом образовательной деятельности становится формирование ключевых компетентностей.
О.Е.Лебедеврассматривает компетентность как «способность действовать в ситуации неопределенности» [11, с.6].
Под ключевыми компетентностями применительно к школьному образованию понимается способность учащихся самостоятельно действовать в ситуации неопределенности при решении проблемы.
О.Е.Лебедев отмечает несколько особенностей такого понимания ключевых компетентностей, формируемых школой.
1. Способности эффективно действовать не только в учебной, но и в других сферах деятельности.
2. Способность действовать в ситуациях, когда может возникнуть необходимость в самостоятельном определении решений задачи, уточнении ее условий, поиске способов решения, самостоятельной оценке результатов.
3. Решение проблем, актуальных для школьника.
И.С.Фишман даёт такое определение компетентности:
«Компетентность – непосредственный результат образования, выражающийся в овладении учащимся определенным набором (меню) способов деятельности»[3].
ИвановД.А., МитрофановК.Г., Соколова О.В.
придерживаются следующего мнения: «
Компетентность – это характеристика, даваемая человеку в результате оценки эффективности/результативности его действий, направленных на, разрешение определенного круга значимых для данного сообщества задач/проблем». [4]
Не следует противопоставлять компетентности знаниям или умениям и навыкам. Понятие компетентности шире понятия знания, или умения, или навыка, оно включает их в себя.
А.В. Хуторскойопределяет компетентность как «владение, обладание человеком соответствующей компетенцией, включающей его личностное отношение к ней и предмету деятельности» [21].
Сам термин «ключевые компетентности» указывает на то, что они являются «ключом», основанием для других, более конкретных и предметно ориентированных. Предполагается, что ключевые компетентности носят надпрофессиональный характер и необходимы в любой области деятельности.
Конкретный набор ключевых компетентностей является предметом запроса работодателей к системе образования, он может варьироваться в связи с актуальной социально-экономической ситуацией в том или ином регионе [22]. В проекте «Концепции реализации на территории Кировской области компетентностно-ориентированного образования» названы следующие ключевые компетентности: рефлексивная, технологическая, проектная, коммуникативная, информационная, социальная.
Рефлексивная компетентность
заключается в готовности организовывать свою деятельность в соответствии с позициями что я делаю (делал, буду делать?), зачем я это делаю (делал, буду делать?), как я это делаю (делал, буду делать?), что я получу (получил) в результате?
Технологическая компетентность
: способность и готовность к пониманию инструкции, описания технологии, алгоритма деятельности, к четкому соблюдению технологии деятельности.
Проектная компетентность
заключается в готовности анализировать ситуацию, выделять проблемы, выдвигать идеи, способствующие решению проблем, ставить цели и соотносить их с устремлениями других людей, программировать и планировать свою деятельность, оценивать результаты своей деятельности.
Коммуникативная компетентность
заключается в готовности получать необходимую информацию, представлять и цивилизованно отстаивать свою точку зрения в диалоге и в публичном выступлении на основе признания разнообразия позиций и уважительного отношения к ценностям (религиозным, этническим, профессиональным, личностным и т.п.) других людей.
Информационная компетентность
заключается в готовности делать аргументированные выводы, осуществлять информационный поиск и извлекать информацию из различных источников на любых носителях, использовать информацию для планирования и осуществления своей деятельности.
Социальная компетентность
заключается в способности соотносить свои устремления с интересами других людей и социальных групп, продуктивно взаимодействовать с членами команды, решающей общую задачу.
И.С.Фишман [
3]
выделяет шесть ключевых компетентностей
· готовность к разрешению проблем,
· технологическая компетентность,
· готовность к самообразованию,
· готовность к использованию информационных ресурсов,
· готовность к социальному взаимодействию,
· коммуникативная компетентность.
Содержание перечисленных ключевых компетентностей раскрывается следующим образом:
Готовность к разрешению проблем
,
то есть готовность анализировать нестандартные ситуации, ставить цели и соотносить их с устремлениями других людей, планировать результат своей деятельности и разрабатывать алгоритм его достижения, оценивать результаты своей деятельности, - позволяет принять ответственное решение в той или иной ситуации и обеспечить своими действиями его воплощение в жизнь.
Технологическая компетентность
,
то есть готовность к пониманию инструкции, описания технологии, алгоритма деятельности, к четкому соблюдению технологии деятельности, - позволяет осваивать и грамотно применять новые технологии, технологически мыслить в тех или иных жизненных ситуациях.
Готовность к самообразованию
, то есть способность выявлять пробелы в своих знаниях и умениях при решении новой задачи, оценивать необходимость той или иной информации для своей деятельности, осуществлять информационный поиск и извлекать информацию различных источников на любых носителях, - позволяет гибко изменять свою профессиональную квалификацию, самостоятельно осваивать знания и умения, необходимые для решения поставленной задачи.
Готовность к использованию информационных ресурсов
, то есть способность делать аргументированные выводы, использовать информацию для планирования и осуществления своей деятельности, - позволяет человеку принимать осознанные решения на основе критически осмысленной информации.
Готовность к социальному взаимодействию
,
то есть способность соотносить свои устремления с интересами других людей и социальных групп, продуктивно взаимодействовать с членами группы (команды), решающей общую задачу, - позволяет использовать ресурсы других людей и социальных институтов для решения задач.
Коммуникативная компетентность
,
то есть готовность получать в диалоге необходимую информацию, представлять и цивилизованно отстаивать свою точку зрения в диалоге и в публичном выступлении на основе признания разнообразия позиций и уважительного отношения к ценностям (религиозным, этническим, профессиональным, личностным и т.п.) других людей, - позволяет использовать ресурс коммуникации для решения задач
Дж. Равен [17] на основе проведенных исследований выделяет следующие ключевые компетентности:
• способность работать самостоятельно без постоянного руководства;
• способность брать на себя ответственность по собственной инициативе;
• способность проявлять инициативу, не спрашивая других, следует ли это делать;
• готовность замечать проблемы и искать пути их решения;
• умение анализировать новые ситуации и применять уже имеющиеся знания для такого анализа;
• способность уживаться с другими;
• способность осваивать какие-либо знания по собственной инициативе (т. е. учитывая свой опыт и обратную связь с окружающими);
• умение принимать решения на основе здравых суждений - т. е. не располагая всем необходимым материалом и не имея возможности обработать информацию математически.
Рассмотрев различные подходы к набору ключевых компетентностей, выделим основные, которые считаем необходимым формировать на уроках математики в основной школе:
· информационная
· коммуникативная
· исследовательская
· готовность к решению проблем
· готовность к самообразованию
2.3 Формирование ключевых компетентностей через учебные математические задачи
По мнению методистов-математиков (Г. И. Саранцев, Е. С. Петрова) важнейшим видом учебной деятельности, в процессе которой школьниками усваивается математическая теория, развиваются их творческие способности и самостоятельность мышления является решение задач. Поэтому ключевые компетентности на уроках математики необходимо формировать через специальные задачи, аналогичные задачам для проверки математической грамотности в исследованиях PISA.
Для формирования информационной компетентности
необходимо использовать задачи содержащие информацию, представленную в различной форме (таблицах, диаграммах, графиках и т.д.). Вопрос задачи может быть сформулирован следующим образом: переведите в графическую (словесную) форму; если возможно, хотя бы приближенно опишите их математической формулой; сделайте вывод, наблюдается ли в этих данных какая-то закономерность и др.
Примером такого задания может быть задача 1
Задача 1
. «Озеро Чад»
На рисунке 1 показано изменение уровня глубины озера Чад в североафриканской части пустыни Сахара. Озеро Чад полностью исчезло примерно 20 000 лет назад до нашей эры в течение последнего Ледникового периода. Примерно 11 000 лет назад до нашей эры оно появилось вновь. Сегодня уровень его глубины примерно такой же, каким он был в 1000 году нашей эры. Какова глубина озера Чад на сегодняшний день?
 
Для формирования коммуникативной компетентности
можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Учащимся можно разделиться на несколько групп, каждая группа должна решить задачу предложенным способом и доказать правильность своего решения оставшимся группам.
Задача, которую можно решить разделившись на группы, приведена ниже:
Задача 2
На гипотенузе АВ прямоугольного треугольника АВС построен квадрат ABDEв той полуплоскости от прямой АВ, которой не принадлежит треугольник АВС. Найти расстояние от вершины С прямого угла до центра квадрата, если катеты ВС и АС имеют соответственно длины aи b.
Решить задачу возможно несколькими способами:
1. используя теорему синусов
2. используя теорему косинусов
3. при помощи метода площадей
4. при помощи метода координат
Для формирования исследовательской компетентности
учащимся можно предложить задания, в которых необходимо исследовать все возможные варианты и сделать определенный вывод.
Задача 3
. «Треугольники»
Обведите букву, которой обозначена фигура, описание которой дается ниже (рисунок приведен в приложении 1). Треугольник PQR прямоугольный с прямым углом R. Сторона RQ меньше стороны PR. M – середина стороны PQ и N – середина стороны QR. S – точка внутри данного треугольника. Отрезок MN больше отрезка MS.
Готовность к разрешению проблем
формируется с помощью задач, в которых необходимо проанализировать предложенную ситуацию, поставить цель, спланировать результат, разработать алгоритм решения задачи, проанализировать результат.
Задача 4
Семья Павловых решила отпраздновать день рождения сына в кафе «Ассоль». Было решено, что их расходы не должны превышать 20 000 рублей. Используя предложенные источники, произведите необходимые расчеты, сделайте вывод и дайте практические рекомендации семье Павловых.
Для начала семья Павловых подготовила список приглашенных на празднование двенадцатого дня рождения сына Сергея. Они решили праздновать его день рождения в кафе «Ассоль», поэтому они взяли прейскурант цен на заказ блюд, напитков, на обслуживание и на дополнительные услуги в данном кафе.
Было решено отмечать день рождение с 16.00 до 22.00. На совете семьи составили меню и список приглашенных (приложение 2).
Для формирования готовности к самообразованию
учащимся необходимо предлагать самостоятельно изучить некоторый теоретический материал, написать реферат, составить задачу и т.д.
Формирование ключевых компетентностей посредством задач позволяет реализовать компетентностный подход на уроках математики как средство повышения математической грамотности учащихся.
Часто одна и та же задача способствует созданию условий для формирования нескольких ключевых компетентностей.
Задачи, способствующие формированию ключевых компетентностей, далее будем называть компетентностно-ориентированными задачами. Таких задач в учебниках и дидактических пособиях немного. Поэтому для реализации компетентностного подхода через задачи единственным выходом для школьных учителей является составление компетентностно-ориентированных задач самим.
Выводы по второму параграфу
Понятие «компетентностный подход» и «ключевые компетентности» получили распространение сравнительно недавно в связи с дискуссиями о проблемах и путях модернизации российского образования. Разные ученые трактуют это понятие по-разному.
В работе мы будем придерживаться определения О.Е.Лебедева, который подкомпетентностным подходом понимает «совокупность общих принципов определения целей образования, отбора содержания образования, организации образовательного процесса и оценки образовательных результатов».
На современном этапе компетентностный подход соответствует социальным ожиданиям в сфере образования, и интересам участников образовательного процесса более, чем традиционный.
С позиции компетентностного подхода основным непосредственным результатом образовательной деятельности становится формирование ключевых компетентностей. «
Компетентность – это способность действовать в ситуации неопределенности». Под ключевыми компетентностями применительно к школьному образованию понимается способность учащихся самостоятельно действовать в ситуации неопределенности при решении проблемы.
Рассмотрев различные подходы к набору ключевых компетентностей, мы выделили основные, которых будем придерживаться в работе:
· информационная
· коммуникативная
· исследовательская
· готовность к решению проблем
· готовность к самообразованию
Так как задача является важнейшим видом учебной деятельности, в процессе которой школьниками усваивается математическая теория, развиваются их творческие способности и самостоятельность мышления, то ключевые компетентности на уроках математики необходимо формировать через специальные задачи, аналогичные задачам для проверки математической грамотности в исследованиях PISA. Такие задачи мы будем называть компетентностно-ориентированными.
3. Компетентностно-ориентированные математические задачи
3.1 Содержание компетентностно-ориентированных математических задач
При решении компетентностно-ориентированных задач основное внимание должно уделяться формированию способностей учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции.
Содержание заданий должно быть связано с традиционными разделами или темами, составляющими основу программ обучения в большинстве стран мира, в том числе и в России: числа, алгебра, функции, геометрия, вероятность, статистика, дискретная математика.
Задачи должны содержать вопросы различных типов – с выбором ответа, с кратким ответом (в виде числа, выражения, формулы, слова и пр.), с развернутым свободным ответом. В первом случае ученик среди предложенных вариантов ответа должен найти верный; во втором – записать свой ответ, не давая при этом никаких пояснений; в третьем случае от ученика требуется записать свое решение, дать обоснование, привести аргументацию. Иногда эти вопросы взаимосвязаны и в процессе их последовательного выполнения учащиеся должны подметить закономерности, выйти на некоторые обобщения. Иногда вопросы являются независимыми, и ответ на последующий вопрос не обусловлен правильностью ответа на предыдущий. В одном и том же задании часто могут быть представлены вопросы разного типа: сначала предлагаются вопросы с выбором ответа, с кратким ответом, а в конце – вопросы с развернутым ответом.
Например, в задании «Гоночная машина» содержатся вопросы с выбором ответа и вопросы, ответ на которые нужно записать.
Задача 5 «
Гоночная машина»
На графике показано, как изменялась скорость гоночной машины, когда она проходила второй круг по трёхкилометровой кольцевой трассе без подъёмов и спусков.
Вопрос 1
Чему примерно равно расстояние от линии старта до начала самого длинного прямолинейного участка трассы?
A 0,5 км
B 1,5 км
C 2,3 км
D 2,6 км
Вопрос 2:
В каком месте трассы скорость машины была наименьшей при прохождении второго круга?
Вопрос 3:
Что можно сказать о скорости машины при прохождении трассы между отметками 2,6 км и 2,8 км?
Вопрос 4:
Ниже изображены пять различных по форме гоночных трасс (рис.2). По какой из этих трасс ехала гоночная машина, график скорости которой приведен ранее? Ответ объясните.

3.2 Три уровня компетентностно-ориентированных
Для составления компетентностно-ориентированных задач по аналогии с тестами PISAразделим их на три уровня (уровень воспроизведения, уровень установления связей, уровень рассуждения). Выделение уровней основывается на уровне математической подготовки учащихся.
Первый уровень (
уровень воспроизведения)
включает воспроизведение математических фактов, методов и выполнение вычислений. Учащиеся могут применять базовые математические знания в стандартных, четко сформулированных ситуациях. Они могут решать одношаговые текстовые задачи, понимают простые алгебраические зависимости, стандартную систему обозначений, могут читать и интерпретировать данные, представленные в таблицах, на графиках, картах, различных шкалах.
Примерами заданий первого уровня могут служить задачи 6 и 7.
Задача 6
«Обменный курс»
Мей-Линг из Сингапура готовилась в качестве студентки по обмену отправиться на 3 месяца в Южную Африку. Ей нужно было обменять некоторую сумму сингапурских долларов (SGD) на южно-африканские рэнды (ZAR).
Вопрос 1
:
После возвращения в Сингапур через 3 месяца у Мей-Линг осталось 3900 ZAR. Она обменяла их снова на сингапурские доллары, обратив внимание на то, что обменный курс изменился следующим образом: 1 SGD = 4,0 ZAR
Сколько денег в сингапурских долларах получила Мей-Линг?
Вопрос 2
:
Мей-Линг узнала, что обменный курс между сингапурским долларом и южно-африканским рэндом был:
1 SGD = 4,2 ZAR
Мей-Линг обменяла 3000 сингапурских долларов на южно-африканские рэнды по данному курсу. Сколько южно-африканских рэндов получила Мей-Линг?
Задача 7
«Увеличение роста»
На графике (рис.3) показан средний рост девушек и юношей в Нидерландах в 1998 году.
| 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
|
| Средний рост девушек в 1998 году |
|

 Вопрос 1
: Объясните, как можно по данному графику определить, что увеличение роста девушек в среднем замедляется после 12 лет.
Вопрос 2
: По сравнению с 1980 годом средний рост 20-летних девушек в 1998 году увеличился на 2,3 см и стал равным 170,6 см. Чему был равен средний рост 20-летних девушек в 1980 году?
Второй уровень (
уровень установления связей)
включает установление связей и интеграцию материала из разных математических тем, необходимых для решения поставленной задачи. Учащиеся могут применять свои знания в разнообразных, достаточно сложных ситуациях. Они могут упорядочивать, соотносить и производить вычисления, решать многошаговые текстовые задачи. Учащиеся могут выполнять несложные алгебраические задания, включающие составление выражений, решение систем линейных уравнений, определять значения величин, используя известные формулы. Они могут интерпретировать информацию, представленную в таблицах и на графиках.
Примерами заданий второго уровня могут служить:
Задача 8
«Скейтборд»
Сергей большой любитель кататься на скейтборде. Он нередко заходит в магазин «Спорт», чтобы выяснить цены на некоторые товары.
В этом магазине можно купить полностью собранный скейтборд. Но можно купить платформу, один комплект из 4 колес, один комплект из двух держателей колес, а так же комплект металлических и резиновых составных частей и собрать свой собственный скейтборд. Цены в магазине на эти товары представлены в таблице 3.
Таблица 3
Цены на части к скейтборду
| Товар |
Цена |
| Собранный скейтборд |
82 или 84 |
 |
| Платформа |
40, 60 или 65 |
 |
| Один комплект из 4 колес |
14 или 36 |
 |
| Один комплект из 2 держателей колес |
16 |
 |
| Один комплект металлических и резиновых деталей скейтборда |
10 или 20 |
 |
Вопрос 1
Сергей хочет сам собрать для себя скейтборд. Какую наименьшую цену и какую наибольшую цену можно заплатить в этом магазине за все составные части скейтборда?
Вопрос 2
В магазине предлагают на выбор три различных вида досок, два различных комплекта колес, два различных комплекта металлических и резиновых деталей. При этом имеется только один выбор комплекта держателей колес.
Сколько различных скейтбордов может собрать Сергей из предлагаемых составных частей?
А. 6
Б. 8
В. 10
Г.
12
Вопрос 3
для задачи «Увеличение роста»:
Пользуясь графиком, определите, в каком возрасте девушки в среднем выше юношей того же возраста
Третий уровень
(уровень рассуждения) - математические размышления, требующие обобщения и интуиции. Учащиеся могут организовывать информацию, делать обобщения, решать нестандартные проблемы, делать выводы на основе исходных данных и обосновывать их. Они могут вычислить изменения имеющихся данных, связанные с процентами, применить знания алгебраических понятий и зависимостей, составить алгебраическую модель несложной ситуации. Они могут интерпретировать, интерполировать и экстраполировать данные в различных таблицах и на графиках
В заданиях третьего уровня, прежде всего, необходимо самостоятельно выделить в ситуации проблему, которая решается средствами математики, и разработать соответствующую ей математическую модель. Решить поставленную задачу используя математические рассуждения и обобщения, и интерпретировать решение с учетом особенностей рассмотренной в задании ситуации.
Примерами заданий, формирующих третий уровень математической грамотности, могут служить:
Вопрос 3
для задачи «Скейтборд»
У Сергея 120 зедов, и он хочет собрать самый дорогой скейтборд, который может позволить себе на эти деньги. Сколько денег он может истратить на каждую из 4 частей скейтборда?
Запишите ответ в приведенную ниже таблицу 4.
Таблица 4
| Части скейтборда |
Сумма денег |
| Платформа |
| Колеса |
| Держатели колес |
| Металлические и резиновые детали |
Вопрос 3
для задачи «Обменный курс»:
За прошедшие 3 месяца обменный курс изменился, вместо 4,2 стал 4,0 ZAR за 1 SGD.
Был ли обменный курс в 4,0 ZAR вместо 4,2 ZAR в пользу Мей-Линг, когда она снова обменяла южно-африканские рэнды на сингапурские доллары?
Задача 9
«Садовник»
 У садовника имеется 32 метра провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов (рис.4). У садовника имеется 32 метра провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов (рис.4).
Таблица 5
| Форма клумбы |
Хватит ли 32 м провода, чтобы обозначить границу клумбы |
| Форма А |
Да\Нет |
| Форма В |
Да\Нет |
| Форма С |
Да\Нет |
| Форма Е |
Да\Нет |
Выводы по третьему параграфу
При решении компетентностно-ориентированных задач основное внимание должно уделяться формированию способностей учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции.
Содержание заданий желательно связывать с традиционными разделами или темами, составляющими основу программ обучения в большинстве стран мира, в том числе и в России: числа, алгебра, функции, геометрия, вероятность, статистика, дискретная математика.
Компетентностно-ориентированные задачи должны содержать вопросы различных типов – с выбором ответа, с кратким ответом (в виде числа, выражения, формулы, слова и пр.), с развернутым свободным ответом.
Мы выделим компетентностно-ориентированные задачи трех уровней, которым присвоены названия: уровень воспроизведения, уровень установления связей, уровень рассуждения. Выделение уровней основывается на уровне математической подготовки учащихся.
4. Методические рекомендации использования компетентностно-ориентированных математических задач
4.1 Содержание учебника математики как среда для составления компетентностно-ориентированных задач
Содержание образования доводится до учителя и учащегося в виде предметного учебно-методического комплекса (УМК), ведущую роль в котором играет учебник. В современных учебниках немного компетентностно-ориентированных заданий (в основном это задачи первого уровня), но на базе имеющихся заданий можно разработать свои задания, формирующие ключевые компетентности. Это означает, что содержание соответствующих параграфов нужно рассматривать как среду, а не как материал, который во что бы то ни стало необходимо усвоить учащимся [10].
Рассмотрим несколько примеров использования задач из учебника, с помощью которых можно составить задание для формирования ключевых компетентностей учащихся.
Задача 10
В учебнике математики для 5 класса [2] предложена следующая задача:
Три рассказа занимают 34 страницы. Первый занимает 6 станиц, а второй – в 3 раза меньше, чем третий. Сколько страниц занимает второй рассказ?
Эта задача не является компетентностно-ориентированной задачей. Добавив к условию задачи вопрос (постройте круговую диаграмму, изображающую распределение страниц по книгам (в процентах))
, задание становится задачей первого уровня, так как учащимся необходимо выполнить несложное вычисление и представить результат в виде диаграммы.
Задача 11
Ю.Ф.Фоминых [19] предлагает следующую задачу: «в романе Жюля Верна «Дети капитана Гранта» читаем: «Погода стояла прекрасная, не слишком жаркая…Роберт узнал, что средняя годовая температура в провинции Виктория +74о
по Фаренгейту». Сколько это будет в привычных для нас градусах Цельсия? Составьте формулу для вычисления температуры в градусах Цельсия, если известна температура по Фаренгейту и наоборот. В таблице 6 приведена температура таяния льда и кипения воды в градусах Цельсия и по Фаренгейту»
Таблица 6
Температура таяния льда и кипения
| Температура |
В градусах Цельсия |
По Фаренгейту |
| Таяния льда |
0 |
32 |
| Кипения воды |
100 |
212 |
Эта задача является заданием первого уровня, так как учащимся необходимо с помощью таблицы составить формулу и используя эту формулу ответить на вопрос задачи. Для того чтобы задача стала заданием второго уровня, добавим в условие задачи несколько вопросов.


Например
: Температура воздуха изменялась в течение дня от 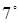 до до 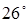 Цельсия. На рисунке 5 изображен график изменения температуры. Изобразите график функции, на котором будет изображена температура воздуха в градусах по Фаренгейту, соответствующая температуре на графике. Цельсия. На рисунке 5 изображен график изменения температуры. Изобразите график функции, на котором будет изображена температура воздуха в градусах по Фаренгейту, соответствующая температуре на графике.
Эта задача будет заданием второго уровня, так как в ходе решения задачи учащимся необходимо определить значения величин по графику и результатом решения задачи так же будет график.
Задача 12
Ю.Ф.Фоминых [19] предлагает следующую задачу: «редактор стенгазеты 8-го класса «Веселая перемена» поместил заметку: «На школьных соревнованиях быстрее всех пробежал стометровку ученик нашего класса Коля. Другие призеры пришли к финишу в таком порядке: Миша, Паша, Федя. И удивительно – с одной и той же разницей в скорости: Коля затратил на эту дистанцию 12 с, Миша – 13 с, Паша – 14 с, Федя – 15 с».
Проверьте, прав ли наш «журналист». Для этого заполните таблицу 7:
Таблица 7
| Коля |
Миша |
Паша |
Федя |
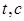 |
12 |
13 |
14 |
15 |
 см/с см/с |
 |
В последней строке поместите разность скоростей каждого мальчика и предыдущего. Действительно ли разница в скорости одна и та же?».
Эта задача является заданием второго уровня, так как решение задачи будет состоять из нескольких шагов, учащимся нужно сравнить получившиеся результаты. Для того, чтобы задача стала заданием третьего уровня можно к условию добавить вопрос: скорость какого из мальчиков ближе к средней скорости бегунов? Результат представьте в виде диаграммы.
Таким образом, задачи из учебника можно использовать в качестве основы для компетентностно-ориентированных заданий.
4.2 Место
компетентностно-ориентированных математических задач в процессе изучения математики
Изучение опыта работы школьных учителей математики (Е. Н. Печенкиной из МОУ «Гимназия № 1 г. Кирова-Чепецка», Е. И. Шехиревой из МОУ СОШ с УИОТ № 21 г. Кирова) и собственный опыт позволили определить место компетентностно-ориентированных задач в процессе изучения математики. Использовать задачи можно, начиная с 5 класса. Чаще всего компетентностно-ориентированные задачи используют на уроках, реже могут использоваться на внеклассных мероприятиях, могут быть предложены в качестве домашнего задания. Компетентностно-ориентированные задания могут использоваться на уроках различных типов: изучения нового материала, закрепления знаний, комплексного применения знаний, обобщения и систематизации знаний, урок контроля, оценки и коррекции.
4.2.1
Компетентностно-ориентированные задачи на уроках изучения нового материала
На уроках изучения нового материала с помощью компетентностно-ориентированной задачи можно создать условия для формирования понятий, вывода и усвоения формул. В качестве примера можно привести урок «Площади многоугольников».
Дидактическая цель:
Создать условия для осознания и осмысления вывода формул площадей параллелограмма, треугольника, трапеции.
Цели по содержанию урока:
1. Образовательная –
способствовать осознанному выводу формул площадей параллелограмма, треугольника, трапеции.
2. Развивающая -
спосо6ствовать формированию умений анализировать, обо6щать и систематизировать информацию.
3. Воспитательная –
спосо6ствовать формированию коммуникативных умений и навыков.
Типурока – изучение нового материала
Форма организации познавательной деятельности —
фронтальная, групповая.
Методы —
частично-поисковый, проблемного изложения материала.
Оборудование:
1. Компьютер и мультимедийный проектор.
2. Наглядный материал (Таблицы 8–11
).
Таблицы 8 – 11 представлены в приложении 3
| № |
Этапы урока |
Деятельность учителя |
Деятельность ученика |
| 1 |
Организационный момент |
Планирует возможность
групповой работы по 4 человека (получается 6 групп);
Проверяет готовность к уроку
|
Проверяют свое рабочее место |
| 2 |
Подготовка к
усвоению нового материала (10 мин):
1. Мотивация
и постановка
целей урока
2. Постановка темы урока
|
Рассказывает об акции добрых дел в
городе Кирово-Чепецке.
Задаёт вопрос: «Что мы можем сделать для 6лагоустройства нашего двора?».
Показывает фотографии
двора школы (Таблица
8)
По ходу обсуждения предложений детей помогает им
сформулировать задачи•
Наводящими вопросами
подводит учащихся к пониманию необходимости получения некоторых новьгх знаний, а именно вывода площади параллелограмма,
,
треугольника, трапеции.
Предлагает учащимся сформулировать тему урока
|
Предлагают различные варианты ответов.
Например:
• можно выложить
дорожки брусчаткой
• можно разбить
клумбы для цветов
• можно создать
клум6ы для декоративной травы
• клумба может
иметь форму трапеции и т.д.
Формулируют задачи
и выполняют к ним
рисунки (Таблица 9).
Формулируют тему урока
|
| 3 |
Освоение нового материала |
Предлагает задание каждой группе:
1 группа – вывести формулу площади параллелограмма, записать ее в таблицу и выполнить чертеж для вывода формулы на листе формата А4
2 группа – вывести формулу площади параллелограмма и осуществить вывод формулы для класса, используя чертеж
3 группа – вывести формулу площади треугольника (считать формулу площади параллелограмма известной), записать ее в таблицу и выполнить чертеж для вывода формулы на листе формата А4
Группа 4 – вывести формулу площади треугольника (считать формулу площади параллелограмма известной), и осуществить вывод формулы для класса, используя чертеж 3 группы
5 группа – вывести формулу трапеции (считать формулу площади треугольника известной), записать ее в таблицу и выполнить чертеж для вывода формулы на листе формата А4
6 группа – вывести формулу площади трапеции (считать формулу площади треугольника известной) и осуществить вывод формулы для класса, используя чертеж 5 группы
Координирует работу групп, при необходимости даёт консультации, Предлагает проанализировать вывод формул и сформулировать о6гций приём,
используемый для вывода
большинства формул (Который будет широко примениться для решения математических задач)
|
Группы получают задание, выполняют его, общаясь при необходимости за помощью к учебнику, к
учителю.
Вывешивают чертежи
на доску, заполняют
таблицу на доске, выписывают на доску
основной вывод формул (Таблица 10, 11).
Анализируют выводы
формул и формулируют общий приём доказательства, предлагая его назвать <Достраивание до знакомой фигуры».
|
| 4 |
Закрепление знаний учащихся |
Призывает вернуться к тексту задач, предложенных в начале урока и решить их по группам с последующим обсуждением |
Делают расчеты в тетради, решают задачи |
| 5 |
Подведение итогов. Рефлексия. |
Задаёт вопросы:
1. достигли Ли цели урока?
2. Что нового узнали на
уроке?
3. где могут пригодиться
полученные знания?
4. над чем необходимо по-
работать дома?
|
Отвечают на вопросы
учителя.
По итогам рефлексии
приходят к выводу,
что для дальнейшей
успешной работы им
необходимо:
1. знать формулы
площадей треугольника, параллелограмма, трапеции
2. Уметь выводить
формулы площадей
треугольника, параллелограмма, трапеции
|
| 6 |
Домашнее задание |
Предлагает домашнее задание №459, 469 |
Записывают домашнее задание |
4.2.2 Компетентностно-ориентированные задачи на уроках комплексного применения знаний
На уроках комплексного применения знаний можно с помощью компетентностно-ориентированных задач можно сформулировать проблему, задачу, которую необходимо решить в течение урока. На уроке «С математикой в путь» учащимся были предложены следующие задачи (разработка урока и карта представлены в приложении 4).
Задача 13
Определить по карте расстояние, которое будет пройдено автомобилем от г.Кирова до г.Сочи. Используя свойство пропорции, рассчитать количество бензина, которое будет затрачено на дорогу, если известно, что на 100 км. требуется 8 литров.
Задача 14
1 литр бензина в 2006 г. стоил 15 рублей. В 2007 г. он подорожал на 13%. Вычислите стоимость бензина в 2007 году?
Задача 15
В таблице 12 указана стоимость билета в плацкартном вагоне.
Таблица 12
Стоимость билета в плацкартном вагоне
| месяц |
стоимость |
| июнь |
1000 р. |
| июль |
1200 р. |
| август |
1500 р. |
Вычислить сумму денег, затраченную семьёй из трёх человек на проезд туда и обратно?
Задача 16
Вычислить количество денег, затраченное на бензин туда и обратно, если известно, что 1л. бензина стоит 17 рублей и израсходовано 156 литров?
Задача 17
Рассчитать количество денег, затраченное на проживание семьи из трёх человек за 13 дней (на 14 день выезжают)?
Таблица 13
| месяц |
Проживание в г.Сочи (на одного человека в сутки) |
| июнь |
250 р. |
| июль |
300 р. |
| август |
350 р. |
Задача 18
Рассчитать количество денег, затраченное семьёй из трёх человек на ночлег в пути(1 ночь, июнь)?
Таблица 14
| месяц |
Ночлег по дороге (на машине) |
| +июнь |
250 р. |
| июль |
270 р. |
| август |
300 р. |
Задача 19
Используя формулу суммы арифметической прогрессии, вычислить сумму денег, затраченную на приобретение газированной воды в дороге, если известно, что в г. Кирове она стоила 7 рублей, а на каждой следующей остановке, где покупали, стоимость увеличивалась на 1,5 рубля? (покупали газ. воду 5 раз)
4.2.3
Компетентностно-ориентированные задачи в качестве домашнего задания
В качестве домашнего задания можно предложить задачу, которую школьники могут решать вместе с родителями. Примером такой задачи может служить
Задача 20
«Ремонт».


Семья Семёновых решила отремонтировать полы в своей квартире, было также решено, что их расходы на ремонт пола не должны превышать 20000 руб. Используя предложенные источники, произведите необходимые расчеты, сделайте вывод и дайте практические рекомендации семье Семеновых, подкрепленные математическими расчетами и содержащие объяснения, почему следует воспользоваться данной рекомендацией.
Для начала Семеновы решили нарисовать план квартиры (рис.6), произведя необходимые измерения, затем приобрести материалы для ремонта пола в квартире. Для этого они отправились в магазин «Строитель». В магазине они взяли рекламный проспект с указанием цен на стройматериалы. На совете семьи было решено постелить в гостиной паркет, в спальне, детской и на кухне – линолеум, в санузле положить кафельную плитку, а в коридоре покрасить пол краской. Для этого им необходимо рассчитать, сколько материалов необходимо приобрести и сколько денег они на это затратят. Для выполнения ремонта было решено обратиться в фирму «Ремонт квартир» и нанять бригаду из 2-х человек. Данная бригада может постелить паркет в комнате за 5 дней, если будет работать по 5 часов в день, постелить линолеум в одной комнате за 2 дня, если будет работать по 5 часов в день, положить плитку в санузле за 2 дня, если будет работать по 5 часов в день, и покрасить полы в одной комнате за 2 дня, если будет работать по 5 часов в день.
Таблица 15
Стоимость работы
| Помещение |
Материал |
Стоимость работы в час (в рублях на 1 человека) |
| Гостиная |
паркет |
70 |
| Санузел |
кафельная плитка |
60 |
| Спальня |
линолеум |
45 |
| Детская |
линолеум |
45 |
| Кухня |
линолеум |
45 |
| Коридор |
краска |
30 |
Таблица 16
Стоимость материала
| Материал |
Количество |
Расцветка |
Цена |
| обои |
 1 рулон 1 рулон |
250 руб. |
| краска |
1 банка (3 кг) |
белая |
180 руб. |
| краска |
1 банка (3 кг) |
голубая |
150 руб. |
| краска |
1 банка (3 кг на покраску 10 м2
пола) |
коричневая |
140 руб. |
| Потолочноепокрытие |
 1 м2 1 м2
|
55 руб. |
| потолочное покрытие |
   1 м2 1 м2
|
75 руб. |
| кафельная плитка |
 1 м2 1 м2
|
225 руб. |
| бордюр |
 1 рулон 1 рулон |
120 руб. |
| плинтус |
1 м |
45 руб. |
| паркет |
 1 м2 1 м2
|
550 руб. |
| линолеум |
 1 м2 1 м2
|
190 руб. |
| клей обойный |
1 упаковка |
75 руб. |
| клей для потолочных покрытий |
1 банка |
65 руб. |
| замазка |
1 банка |
45 руб. |
Выводы по четвертому параграфу
Содержание образования доводится до учителя и учащегося в виде предметного учебно-методического комплекса (УМК), ведущую роль в котором играет учебник. Используя учебник, на базе имеющихся заданий можно разработать свои задания, формирующие ключевые компетентности, то есть компетентностно-ориентированные задачи. Это означает, что содержание соответствующих параграфов нужно рассматривать как среду для разработки компетентностно-ориентированных задач.
Чаще всего компетентностно-ориентированные задачи используют на уроках, могут быть предложены в качестве домашнего задания. Как показало изучение опыта работы учителей математики, компетентностно-ориентированные задания могут использоваться на уроках различных типов: изучения нового материала, закрепления знаний, комплексного применения знаний, обобщения и систематизации знаний, контроля, оценки и коррекции.
5. Опытное преподавание в 9 классе
Цель: Проверить эффективность методических рекомендаций путем опытного преподавания.
Школа: МОУ СОШ № 40 г. Кирова
Класс: 9 б
Учитель: Е.А.Щенникова
Содержание.
В ходе опытного преподавания было проведено три урока алгебры. Перед началом опытного преподавания учащимся была предложена задача «Обменный курс». В результате с заданием первого уровня справились 63 %, с заданием первого и второго уровней – 24 %, с заданием первого, второго и третьего уровня – 8 %. Остальные испытывали затруднения при решении задачи.
Далее были проведены три урока, посвященные решению задач «на проценты», «на движение», «на площади и периметры» (Приложение 5).
На этих уроках использовалась фронтальная, групповая и индивидуальная формы организации познавательной деятельности. В основном использовались частично-поисковый и исследовательский методы.
По мнению Е.А.Щенниковой (отзыв прилагается) «использование компетентностно-ориентированных задач на уроках позволило создать условия для развития способностей учащихся распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены средствами математики, формулировать эти проблемы на языке математики, решать эти проблемы, используя математические знания и методы, анализировать использованные методы решения, интерпретировать полученные результаты с учетом поставленной проблемы, формулировать и записывать окончательные результаты решения поставленной проблемы».
После трех уроков решения компетентностно-ориентированных задач учащимся этого класса была предложена задача «Скейтборд» Процент учащихся, справившихся с заданием первого уровня, составил 53 %, с заданием первого и второго уровня – 31 %, с заданием первого, второго и третьего уровня – 16 %.
На диаграмме 1 наглядно видно, как изменились результаты учащихся после использования компетентностно-ориентированных задач на уроках математики.
Диаграмма 1
| Количество учащихся, справившихся с заданиями первого, второго и третьего уровня |
|
| Количество учащихся, справившихся с заданиями первого и второго уровня |
|
| Количество учащихся, справившихся с заданиями первого уровня |
|
 Следовательно, можно утверждать, что использование компетентностно-ориентированных задач на опытных уроках математики способствует повышению математической грамотности учащихся.
Заключение
Формирование ключевых компетентностей на уроках математики в основной школе занимает особое место. Применение компетентностно-ориентированных заданий позволяет решить проблему более качественного усвоения знаний по математике и способности их применения на практике.
В ходе выполнения работы были получены следующие выводы:
1. С точки зрения разработчиков международных исследований PISA под математической грамотностью понимается «способность человека определять и понимать роль математики в современном мире, применять математику для решения проблем».
2. Проанализировав научную и научно-методическую литературу по данной теме, были рассмотрены теоретические основы реализации компетентностного подхода при обучении математике, основные принципы и классификации ключевых компетентностей. При сравнении традиционного и компетентностного подходов выделены основные преимущества компетентностного подхода, выявлена его роль в процессе обучения математике учащихся основной школы.
3. Рассмотрев содержательный аспект, определив уровни компетентностно-ориентированных задач и изучив опыт работы учителей математики, были разработаны методические рекомендации по составлению и использованию задач на уроках математики.
4. В исследовательской части были приведены результаты деятельности учащихся до использования компетентностно-ориентированных задач на уроках математики, и после использования. Выводы сделанные по этой части работы только подтверждают правильность выдвинутой гипотезы. То есть использование компетентностно-ориентированных задач на уроках математики повышает математическую грамотность. Подводя итоги всего выше сказанного, считаю, что цель работы достигнута, задачи выполнены.
Список библиографии
1. Атанасян, Л.С. Геометрия [Текст]/ Л.С. Атанасян: Учебник для 7-9 классов средней школы. – М.: Просвещение, 1992. – 335 с.
2. Виленкин, Н.Я. и др. Математика [Текст]/ Н.Я. Виленкин : Учебник для 5 класса общеобразовательных учреждений – М.: Издательство «Русское слово», 1998. – 358 с.
3. Загребина, М.Г., Плотникова, А.Ю., Севостьянова, О.В., Смирнова И.В. Тесты внешней оценки уровня сформированности ключевых компетентностей учащихся: Методическое пособие для руководителей и педагогов образовательных учреждений / Под ред. И.С. Фишман [Текст]. – Вып. 2 – Самара, 2006.
4. Иванов, Д.А., Митрофанов, К.Г.,
Соколова, О.В.
Компетентностный подход в образовании. Проблемы, понятия, инструментарий. Учебно-методическое пособие [Текст]/ Д.А. Иванов, К.Г.Митрофанов, О.В. Соколова,.-М.: АПКиППРО, 2005.—101 с.
5. Кларин,М. Педагогические технологии и инновационные тенденции в современном образовании (зарубежный опыт) [Текст]/ М. Кларин// Инновационное движение в российском школьном образовании. - М., 1997. - с. .337.
6. Ковалева, Г.С., Красновский, Э.А., Краснокутская, Л.П., Краснянская, К.А. Оценка знаний и умений. Международная программа PISA [Текст]/ Г.С. Ковалева, Э.А. Красновский, Л.П. Краснокутская, К.А. Краснянская // Школьные технологии №6 2006 г., с. 203-217
7. Ковалева, Г.С., Краснянская, К.А. Результаты третьего международного исследования по оценке качества математического и естественнонаучного образования в России [Текст]/ Г.С. Ковалева, К.А. Краснянская, // Школьные технологии № 4 2001 г, с. 125-136
8. Компетентностный подход // Школьные технологии №1, 2005 год, с.7
9. Компетентностный подход как способ достижения нового качества образования – Материалы для опытно-экспериментальной работы в рамках Концепции модернизации российского образования на период до 2010 года [Текст]. - М., 2002. - с. 7 – 54
10. Курганов, С.Ю. Ключевые учебные ситуации и тестирование [Текст] / С.Ю. Курганов// Школьные технологи №4, 2006 г., с.97-102
11. Лебедев, О.Е. Компетентностный подход в образовании [Текст] / О.Е Лебедев // Школьные технологии №5, 2004 год, с.3
12. Макарычев, и др. Алгебра [Текст]: Учебник для 9 класса средней школы/ Под ред. С.А.Теляковского – М.: Просвещение, 1990. – 272 с.
13. Меерович, М.И.. Шрагина, Л.И. Технология творческогомышления: практическое пособие.[Текст]/ М.И. Меерович, Л.И. Шрагина - Мн.: Харвест, М: АСТ, 2000. - с. 12. 28
14. Нефедова, Л.А., Ухова, Н.М. Развитие ключевых компетенций в проектном обучении [Текст]/ Л.А. Нефедова, Н.М. Ухова,// Школьные технологи №4, 2004 г., с. 61-64
15. Основные результаты международного исследования образовательных достижений учащихся PISA-2003 [Текст]. – М, 2004
16. Приказ №393 от 11.02.2002 О Концепции модернизации российского образования на период до 2010 года [Текст. http://www.edu.ru/db/mo/Data/d_02/393.html
17. Равен, Дж. Компетентность с современном обществе. [Текст]/ Дж. Равен -М.: Когито-центр, 2002
18. Саранцев, Г.И. Методика обучения математике в средней школе: Учеб. Пособие для студентов мат. Спец. Пед. Вузов и унт-ов/ Г.И. Саранцев– М.: Просвещение, 2002.- 224 с.
19. Фоминых, Ю.Ф. прикладные задачи по алгебре для 7-9 классов: Кн. Для учителя. [Текст]/ Ю.Ф. Фоминых– М. Просвещение, 1999. – 112 с.
20. Фрумин, И.Д. Компетентностныйподход как естественныйэтап обновления содержания образования [Текст]/ И.Д. Фрумин // Педагогика развития: ключевые компетентности и их становление: Материалы 9-й научно-практической конференции. - Красноярск, 2003. -с. 55.
21. Хуторской, А.В. Ключевые компетенции и образовательные стандарты [Текст]/ А.В. Хуторской // Интернет-журнал "Эйдос". - 2002. - 23 апреля.
22. Ярулов, А.А. Познавательная компетентность школьников [Текст]/ А.А. Ярулов // Школьные технологии №2, 2004 год, с.43-84.
23. www.portal-slovo.ru
Приложение 1
Рисунок к задаче 3 «Треугольники».
Приложение 2
Таблицы к задаче 4
Список приглашенных
Семья Павловых:
1. Мария Владимировна (мама)
2. Петр Сергеевич (папа)
3. Сергей (именинник)
4. Марина (младшая сестра)
|
Родственники
:
1. Павлова Зоя Васильевна (бабушка)
2. Павлов Дмитрий Федорович (дядя)
3. Павлов Миша (двоюродный брат)
4. Павлова Света (двоюродная сестра)
|
Друзья:
1. Исаев Андрей
2. Ковалев Максим
3. Карташова Лиза
|
4. Зацепин Слава
5. Валеева Оксана
6. Лапин Олег
7. Кораблев Саша
|
Прейскурант цен на заказ блюд
| № |
Название |
К-во |
Цена (у. ед*
) |
| Бутерброды: |
| 1 |
Бутерброды с бужениной |
1 шт |
0,7 |
| 2 |
Бутерброды с помидорами |
1 шт |
0,4 |
| 3 |
Бутерброды с паштетом и яблоками |
1 шт |
0,6 |
| 4 |
Бутерброды «Кораблик»
(хлеб, сельдь, картофель, огурцы, лимон, майонез)
|
1 шт |
0,7 |
| 5 |
Бутерброды «Парус»
(хлеб, сливочное масло, твердый сыр, петрушка)
|
1 шт |
0,8 |
| 6 |
Бутерброды с сыром и фруктами |
1 шт |
0,8 |
| 7 |
Канапе с ветчиной и огурцом |
1 шт |
0,6 |
| 8 |
Канапе с сельдью и яблоками |
1 шт |
0,7 |
| 9 |
Канапе с лососиной |
1 шт |
1,1 |
| 10 |
Канапе с языком и сыром |
1 шт |
1,2 |
| 11 |
Канапе с грибами и яйцом |
1 шт |
0,9 |
| Салаты: |
| 1 |
Салат из ананаса с сельдереем
(ананас, сельдерей, свекла, салат, растительное масло)
|
150 г |
1,7 |
| 2 |
Салат «Деликатесный»
(помидор, огурцы, спаржа, фасоль, зеленый горошек, цветная капуста, салат, майонез)
|
150 г |
1,3 |
| 3 |
Русский салат
(мясо, огурцы, зеленый лук, яйца, зелень, майонез)
|
150 г |
1,5 |
| 4 |
Салат с сельдью и крабами
(сельдь, картофель, соленые огурцы, морковь, лук, крабы, салат, горчица, майонез)
|
150 г |
2,3 |
| 5 |
Салат «Столичный»
(мясо птицы, картофель, соленые огурцы, салат, маслины, соус «Южный», майонез)
|
150 г |
1,8 |
| Супы: |
| 1 |
Рассольник |
1 порция |
1,2 |
| 2 |
Щи с грибами |
1 порция |
1,4 |
| 3 |
Солянка |
1 порция |
2,3 |
| 4 |
Суп – пюре из куриной печени |
1 порция |
1,6 |
| 5 |
Суп рыбный с фрикадельками |
1 порция |
1,5 |
| Горячие блюда: |
| 1 |
Беф – строганов |
1 порция |
2,9 |
| 2 |
Бифштекс с картофелем |
1 порция |
2,8 |
| 3 |
Шницель рубленный |
1 порция |
2,6 |
| 4 |
Чанахи |
1 порция |
3,7 |
| 5 |
Шашлык из молодой баранины |
1 порция |
3,5 |
| 6 |
Котлеты пожарские |
1 порция |
3 |
| 7 |
Зразы из говяжей вырезки |
1 порция |
4,1 |
| 8 |
Цыплята, жаренные в тесте |
1 порция |
3,7 |
| 9 |
Зразы из рыбы и грибов под соусом |
1 порция |
4,3 |
| 10 |
Треска по - польски |
1 порция |
4 |
| 11 |
Осетрина, запеченная с грибами |
1 порция |
5,7 |
| 12 |
Карпы, жаренные во фритюре |
1 порция |
4,8 |
| Десерты: |
| 1 |
Пудинг из сливок и бисквита |
1 порция |
2 |
| 2 |
Шарлотка из яблок |
1 порция |
1,8 |
| 3 |
Мусс из апельсинов |
1 порция |
1,6 |
| 4 |
Самбук из яблок |
1 порция |
1,5 |
| 5 |
Вишни в кляре |
1 порция |
1,6 |
| 6 |
Торт «Киевский» |
1 шт (1 кг) |
8 |
| 7 |
Торт слоеный с вареньем и взбитыми сливками |
1 шт (1 кг) |
7,3 |
| 8 |
Персики в креме |
1 порция |
2,9 |
| 9 |
Сливочный пломбир с ананасом и дыней |
150 г |
2,7 |
| 10 |
Пломбир с вареными грушами и ореховым печеньем |
150 г |
2,5 |
| 11 |
Желе шоколадное |
1 порция |
2,3 |
| Напитки: |
| 1 |
Шоколад |
1 порция |
1,5 |
| 2 |
Какао с мороженым |
1 порция |
1,6 |
| 3 |
Крюшон клубничный |
1 порция |
1,3 |
| 4 |
Коктейль фруктовый с мороженым |
1 порция |
1,7 |
| 5 |
Коктейль шоколадный |
1 порция |
1,3 |
| 6 |
Сок фруктовый |
1 л |
1,3 |
| 7 |
Чай |
1 порция |
1 |
| 8 |
Кофе |
1 порция |
1 |
| Шоколадные конфеты |
1 кг |
3 |
| Фрукты: |
| 1 |
Яблоки |
1 кг |
2 |
| 2 |
Груши |
1 кг |
2,2 |
| 3 |
Бананы |
1 кг |
1,3 |
| 4 |
Апельсины |
1 кг |
1,4 |
| 5 |
Персики |
1 кг |
2,4 |
Дополнительные услуги
| Название услуги |
К-во |
Цена |
| Официант |
1 |
100 руб/ч |
| Ведущий |
1 |
200 руб/ч |
| Актер (в костюме клоуна, скомороха и т. п.) |
1 |
150 руб/ч |
| Музыкальное оформление (магнитофон) |
- |
0 руб/ч |
| Вокально-инструментальный ансамбль |
1 группа |
1150 руб/ч |
| Хореографическая группа |
1 группа |
950 руб/ч |
| Саксофонист |
1 |
700 руб/ч |
| Баянист |
1 |
500 руб/ч |
| Украшение зала (шары, цветы, плакаты) |
(по заказу клиента) |
750 руб |
Приложение 3
Таблицы для урока «Площади многоугольников»
 
 

Задача 1
Клумба имеет размеры:

На 1 м2
необходимо 20 семян. Количество клумб – 5. сколько семян нужно для засевания клумб?
Задача 2
Брусчатка имеет размеры:

Площадь дорожки равна 1000 м2
. сколько укладки нужно для укладки дорожки?
Задача 3
Газоны имеют размеры

На 1 м2
необходимо 20 семян. Количество газонов – 5. сколько семян декоративной травы нужно для засевания газонов?


Приложение 4
Разработка урока «С математикой в путь».
Дидактическая цель:
Создать условия для применения знаний и умений в знакомой обстановке и новых учебных ситуациях.
Цели по содержанию урока:
1. Образовательная
- способствовать осознанию того, что темы, изученные на уроках математики широко применяются в повседневной жизни.
2. Развивающая
– способствовать обучению школьников умению выделять математическую модель из практико – ориентированной задачи.
3. Воспитательная
– способствовать эстетическому и экономическому воспитанию учащихся.
Тип урока – комплексное применение знаний и умений.
Форма организации познавательной деятельности – фронтальная, групповая, индивидуальная, парная.
Методы – частично – поисковый, проблемного изложения материала.
Оборудование:компьютер, тетрадь на печатной основе, карта – схема.
| Этапы урока |
Цель каждого этапа |
Деятельность учителя |
Деятельность ученика |
| 1.Организационный момент. |
Создать психологический настрой |
Приветствует учащихся |
Проверяют готовность к уроку |
| 2.Целеполагание и мотивация. |
Организовать и направить деятельность учащихся на постановку целей урока и на формулировку темы урока. |
а) мотивация
Ведёт беседу по следующим вопросам:
1) Любите ли вы путешествовать?
2) Какими видами транспорта можно воспользоваться?
б) постановка темы урока
Предлагает отправиться в путешествие в г.Сочи на поезде или на машине, а для этого нужны некоторые расчёты.
в) постановка цели урока
Формулирует задачу:
«На семейном совете семья Ивановых, состоящая из трёх человек, решила отправиться в июне месяце на отдых в г. Сочи. Была выделена сумма в размере 35000 рублей. Используя информацию, полученную на уроке, посоветовать семье Ивановых перечень экскурсий »
|
Отвечают на вопросы учителя.
Формулируют тему урока.
Формулируют цель урока:
Рассчитать сумму, которая может быть потрачена на экскурсии и посоветовать перечень экскурсий на полученную сумму.
|
| 3.Актуализация знаний и умений |
Повторить знания , полученные в 9 классе и рассчитать нужные затраты. |
По вариантам предлагает решить предложенные задачи, чтобы разгадать слово, зашифрованное на доске.
Координирует работу учащихся.
|
Решают задачи, находят нужные буквы, разгадывают фразу.
|
| 4.Применение знаний в изменённой ситуации |
Организовать деятельность учащихся для применения полученной информации |
Предлагает заполнить таблицу,
Координирует работу учащихся.
|
Заполняют предложенную таблицу (таблица 2 и таблица 3) , предлагают перечень экскурсий. |
| 5.Информация о домашнем задании. |
Дорешать задачи, которые не успели в классе. |
Записывают домашнее задание. |
| 6.Рефлексия. |
Проговорить темы, повторённые на данном уроке,
Выявить эмоциональный настрой учащихся.
|
Предлагает заполнить |
Заполняют предложенную таблицу. |
| ПЛАН |
ПОЕЗД
|
МАШИНА
|
1)
Билеты
Сумма, потраченная на бензин
|
2)
Постельное бельё
.
Проживание в дороге
|
| 3) Проживание семьи за 14 дней.
|
| 4) Питание за 14 дней.
|
| 5) Потраченная сумма.
|
| 6) Оставшаяся сумма.
|
Рефлексия
| Название темы |
Знак «+»
|
| 1) Арифметическая прогрессия. |
| 2) Проценты. |
| 3) Решение текстовых задач. |
| 4) Геометрическая прогрессия. |
| 5) Линейная функция. |
| 6) Чтение графика. |
| 7) Масштаб |
| 8) Приближённые вычисления. |
| ПЛАН |
ПОЕЗД
|
МАШИНА
|
1)
Билеты
Сумма, потраченная на бензин
|
6000 |
5304 |
| 2)
Постельное бельё
. Проживание в дороге
|
330 |
750 |
| 3) Проживание семьи за 14 дней.
|
9750 |
9750 |
| 4) Питание за 14 дней.
|
9800 |
9800 |
| 5) Потраченная сумма.
|
25880 |
25604 |
| 6) Оставшаяся сумма.
|
9120 |
9396 |
Рабочая тетрадь ученика
Группа, состоящая из 20 человек, имеет в наличии 170 000 рублей. Требуется выбрать оптимальный вид транспорта и составить экскурсионную программу для путешествия в июне месяце.
Таблица – помощница
Дорогие ребята!
Перед вами тексты задач, которые помогут вам осуществить вашу мечту – путешествие. Начните решение с той задачи, которая соответствует цвету вашего варианта. Если вы справились со своими заданиями, продолжайте решение следующих задач.
В добрый путь!
Прорешав задачи, заполните таблицу:
Рефлексия
| Поезд
|
Автобус
|
| 1
|
Билеты
|
Сумма, потраченная на бензин
|
| 2
|
Постельное бельё
|
Проживание в дороге
|
| 3
|
Питание в дороге
|
Питание в дороге
|
| 4
|
Проживание семьи за 14 дней
|
Проживание семьи за 14 дней
|
| 5
|
Питание за 14 дней
|
Питание за 14 дней
|
| 6
|
Потраченная сумма
|
Потраченная сумма
|
| 7
|
Оставшаяся сумма
|
Оставшаяся сумма
|
Запишите темы, которые вы повторили в ходе урока
1. ______________________________________________________
2. ______________________________________________________
3. ______________________________________________________
4. ______________________________________________________
5. ______________________________________________________
6. ______________________________________________________
7. ______________________________________________________
Приложение 5
Задачи для опытного преподавания
Задачи на проценты
Актуализация знаний
Рассмотрим задачу:
В комиссионном магазине цена товара, выставленного на продажу, уменьшается на одно и то же число % от прежней цены. Определите, на сколько % каждый месяц уменьшалась цена магнитофона, если выставленный на продажу за 4 тыс. рублей после двух снижений он был продан за 2250 рублей?
Какие формулы необходимо вспомнить, чтобы решить эту задачу?
Задачи:
Блок 1
Работа в группах
· Класс разбивается на группы по 3-4 человека; группы формируются для данной работы примерно равные по силам;
· Учитель ставит перед учащимися цель групповой работы: задачи решаются одна за другой всеми учащимися с обязательным обсуждением решения в группе.
· Считается, что группа решила задачу только тогда, когда каждый член группы может объяснить решение у доски, в этом случае все члены группы поднимают руки, заявляя, тем самым, о своей готовности;
· Учитель вызывает любого ученика из этой группы для доклада, при этом учащиеся остальных групп прекращают решение задачи и принимают роль оппонентов; если какая-то группа во время доклада заметила ошибку, то она сообщает об этом поднятием рук;
· После окончания доклада предложенное решение обсуждается, и выставляются баллы в зависимости от сложности задачи и правильности решения; правильные действия оппонентов также поощряются; после этого осуществляется переход к следующей задаче;
Задача №1
Стоимость жилья в городе N.
| Средняя цена 1 м2
общей площади в у.е. |
Поправочные коэффициенты, влияющие на стоимость квартиры |
| Номер зоны |
Количество комнат |
Параметры |
Примечание |
% |
| 1 |
2 |
3 |
Этаж
|
Первый |
-3 |
| 1 |
875 |
906 |
931 |
Последний |
-1 |
| 2 |
628 |
647 |
659 |
Не крайний |
0 |
| 3 |
639 |
659 |
668 |
Лифт |
Нет |
-1 |
| 4 |
596 |
624 |
635 |
Есть |
+1 |
| 5 |
574 |
604 |
622 |
Балкон |
Балкон/лоджия |
+1 |
| 6 |
611 |
631 |
664 |
Без балкона |
-1 |
| 7 |
605 |
624 |
648 |
Мусоропровод |
Нет |
-1,5 |
| 8 |
616 |
635 |
652 |
Есть |
0 |
| 9 |
713 |
728 |
743 |
Окна
|
Двор |
+2,5 |
| 10 |
721 |
742 |
769 |
Двор, улица |
0 |
| 11 |
622 |
639 |
658 |
Улица |
-2 |
| 12 |
699 |
684 |
679 |
Оцените, сколько примерно будет стоить один квадратный метр в трехкомнатной квартире на втором этаже пятиэтажного дома с балконом, мусоропроводом, окнами во двор и без лифта, если она находится в четвертой зоне.
Задача № 2
Три человека в течении дня пользовались мобильной связью и звонили по одному и тому же номеру.
· Первый звонил вечером,
· Второй звонил днем по увеличенному на 50% тарифу,
· Третий звонил в ночное время со скидкой 75%.
Все они говорили по 5 минут. Телефонная станция прислала общий счет на 66 р. Сколько должен заплатить каждый?
Задача № 3
Человек обычно получает за работу «чистыми», т.е. после вычета налога в 13%, но ему интересно узнать, сколько же «по-настоящему» стоит сделанная им работа, если он получил за нее 3400 р.
Задача № 4
Население острова ежегодно увеличивается на 2%. Какой станет численность населения острова через 5 лет, если на данный момент она составляет 200000 человек?
Задача № 5
Сколько денег получит вкладчик через 5 лет, если он положит на счет 1500 р. И ни разу не будет брать деньги со счета, а тем временем сумма будет ежегодно увеличиваться на 10%?
Блок 2
Совместная работа с учителем
Задачи решаются совместно всеми учащимися.
Задача №1
Студент ежемесячно получает стипендию в размере 500 р., которую не тратит, а сразу кладет в банк, начисляющий 1 % в месяц. Какой составится капитал по окончанию университета, т.е. через 60 месяцев, при условии, что все выплаченные стипендии отданы в рост на описанных условиях?
Задача № 2
Новый компьютер был куплен за S р. И каждый год на амортизацию списывается p% его первоначальной стоимости. Через сколько лет этот компьютер можно списать как полностью потерявший первоначальную стоимость?
(Замечание: обычно в качестве процента амортизации принимают p=15%)
Задача № 3
Два предпринимателя в один и тот же день организовали свои предприятия. У одного из них начальный капитал 3 млн. р. И чистый доход 20% в год, а у другого 0,5 млн. р. И 120% в год соответственно. Определите, настанет ли такой момент, когда оба предпринимателя будут иметь одинаковые капиталы?
Указание: можно составить зависимость суммы на счете от времени в виде функции.
Задача № 4
Имеется 2 сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Блок 3
Самостоятельная работа
Учащиеся самостоятельно решают задачи, затем обсуждают решение.
Задача № 1
Сколько надо заплатить, если платеж 5000 р. Пеня равна 1% за каждый день просрочки, а оплата производится с задержкой на 5 дней?
Задача № 2
За весну Обломов похудел на 25%, затем за лето прибавил в весе 20%, за осень похудел на 10%, а за зиму прибавил 20%. Похудел ли он или поправился за год?
Задачи для домашнего задания
1.Средняя зарплата в России в середине 1993 г. составляла 120000 р. К концу года она увеличилась на 50%.
1) На сколько рублей увеличилась средняя зарплата?
2) Какой стала зарплата к концу года?
2.В состав одного из поливитаминов входят минералы в следующих количествах: кальций и фосфор – по 4%, магний – 1,6%, железо – 0,07%, цинк – 0,06%. Сколько миллиграммов каждого минерала содержится в одной таблетке поливитамина, масса которой 25 г?
3.Два слитка, один из которых содержит 35% серебра, а другой 65%, сплавляют и получают слиток массой 20 г., содержащий 47% серебра. Какова масса каждого из этих слитков?
Задачи на движение
Актуализация знаний
1.Что означачают следующие формулы
V
= t
: S
t
= s
: V
S
= t
х V
2. Чем отличается движение по воде от движения по суше? Какими формулами выражается движение по течению и движение против течения?
(V no
теч
=
Vc
+ Vтеч
;
V np.
теч
=
Vc
- V теч
.)
3. Вспомните, как находят скорости при движении в одном направлении, при движении в разных направлениях?
Задания для фронтальной работы
Задача №1
Прочитайте задачу: «От турбазы до станции турист доехал на велосипеде за 4 часа. На мопеде он смог бы проехать это расстояние за 2 часа. Известно, что на мопеде он едет со скоростью, на 9 км/ч большей, чем на велосипеде. Чему равно расстояние от турбазы до станции?»
Выберите уравнение, соответствующее условию задачи, если за х обозначено расстояние (в км.) от турбазы до станции.
1. 
2. 
3. 
4. 
Задача №2
Утром по дороге в школу ученик 5 класса Марат собирался переходить улицу и увидел проезжающую машину. Ширина улицы 10м, Марат находится на расстоянии 6м от края дороги, машина на расстоянии 100м. Стоит ли ему переходить через улицу или подождать и пропустить машину, если его скорость 80м/мин, а скорость машины: 60км/ч, 80км/ч?
Ответ: машине потребуется 6с или 4, 5с, Марату 12с.
Задача № 3
От вулканостанции до вершины вулкана идти 4 часа по дороге, а затем - 4 часа по тропинке. На вершине расположено два кратера. Первый кратер 1 час извергается, потом 17 часов молчит, потом опять 1 час извергается и т. д. Второй кратер 1 час извергается, 9 часов молчит, 1 час извергается и т. д. Во время извержения первого кратера опасно идти и по тропинке, и по дороге, а во время извержения второго опасна только тропинка. Ваня увидел, что ровно в 12 часов оба кратера начали извергаться. Сможет ли он когда-либо подняться на вершину вулкана и вернуться назад, не рискуя жизнью?
Задача № 4
Марат , стоя на краю тротуара, увидел медленно едущий грузовик, расстояние до которого было около 100м.Ширина улицы 16м, скорость грузовика 45км/ч, скорость Марата 120м/мин. Сумеет ли Марат перейти улицу без осложнений? Каковы будут последствия для Марата, если из-за грузовой машины выскочит на скорости 81км/ч маршрутное такси, которое Марат не заметил? Сколько людей могут получить травму в результате небрежности одного школьника?
Ответ: Марату потребуется 8с на переход, грузовику -8с, он успеет перебежать перед грузовиком. Маршрутному такси потребуется 4, 4с и оно встретится с Маратом посередине дороги
Задания для самостоятельной работы
Задача №1.
Сергею, который живет в Красноармейске, необходимо встретить сестру, которая должна приехать в Москву на поезде. Сергею известно:
1. Сестра приезжает на Курский вокзал
2. Номер поезда - 078д
В какое время необходимо выехать Сергею, что бы успеть к поезду, если скорость автомобиля – 70 км/ч.
(Карта Московской области и расписание поездов прилагается).
Задачи для домашнего задания
Рассчитайте примерную скорость, с которой вы идете от школы до дома.
Карта Московской области

Расписание поездов, прибывающих на Курский вокзал
| № поезда |
Время прибытия |
Время отправления |
| 024с |
Адлер |
09.27. |
Скор. |
Ежедневно |
39.50. |
17.37. |
| 076с |
Адлер |
14.25. |
Скор. |
По чётным |
40.46. |
21.39. |
| 222с |
Адлер |
05.59. |
Скор. |
Ежедневно |
36.51. |
17.08. |
| 072в |
Белгород, "Белгород" |
08.54. |
Фирм. |
Ежедневно |
11.04. |
21.50. |
| 070п |
Бердянск |
10.26. |
Скор. |
Ежедневно |
23.56. |
09.30. |
| 198п |
Бердянск |
16.50. |
Скор. |
Ежедневно |
23.50. |
16.00. |
| 058в |
Валуйки, "Старый Оскол" |
06.25. |
Фирм. |
Ежедневно |
15.49. |
14.36. |
| 604м |
вагон из Валуек |
06.14. |
Фирм. |
По нечётным |
13.51. |
16.23. |
| 121с |
Владикавказ (в Санкт-Петербург) |
19.32. |
Скор. |
По чётным |
44.32. |
23.00. |
| 016п |
Днепропетровск, "Приднепровье" |
09.12. |
Фирм. |
Ежедневно |
17.57. |
14.15. |
| 010д |
Донецк |
10.31. |
Скор. |
Ежедневно |
18.44. |
14.47. |
| 114д |
Донецк, "Донецкий" |
05.30. |
Фирм. |
По нечётным |
19.55. |
08.35. |
| 026п |
Евпатория |
20.29. |
Скор. |
Ежедневно |
24.00. |
19.29. |
| 232с |
Ейск |
14.30. |
Скор. |
Ежедневно |
28.23. |
10.07. |
| 132г |
Ижевск (в Санкт-Петербург) |
21.16. |
Скор. |
По нечётным |
23.11. |
22.05. |
| 098п |
Керчь |
11.35. |
Скор. |
Ежедневно |
26.07. |
08.28. |
| 027с |
Кисловодск |
06.48. |
Скор. |
Ежедневно |
34.43. |
20.05. |
| 049ч |
Кисловодск (в Санкт-Петербург) |
01.49. |
Скор. |
Ежедневно |
36.24. |
13.25. |
| 074п |
Кривой Рог |
14.53. |
Скор. |
Ежедневно |
24.13. |
13.40. |
| 010д |
вагон из Купянска |
10.31. |
Скор. |
Ежедневно |
17.18. |
16.13. |
| 082м |
Курск (в Санкт-Петербург) |
03.15. |
Скор. |
По нечётным |
07.50. |
19.25. |
| 106ч |
Курск, "Соловей" |
06.54. |
Фирм. |
Ежедневно |
08.34. |
22.20. |
| 604м |
вагон из Ливен |
06.14. |
Фирм. |
По пн, чт и вс |
15.53. |
14.21. |
| 142м |
Льгов, "Сейм" |
20.05. |
Фирм. |
Ежедневно |
10.31. |
06.36. |
| 832в |
Льгов |
12.14. |
Приг. |
По пн, пт и сб |
07.36. |
04.38. |
| 078д |
Мариуполь |
11.11. |
Скор. |
Ежедневно |
23.21. |
10.50. |
| 148д |
Мариуполь (в Санкт-Петербург) |
01.17. |
Скор. |
По нечётным |
24.46. |
23.31. |
| 021г |
Нижний Новгород, "Нижегородец" |
06.10. |
Фирм. |
Ежедневно |
07.25. |
22.45. |
| 059г |
Нижний Новгород (в Санкт-Петербург), "Волга" |
00.55. |
Фирм. |
Ежедневно |
06.35. |
18.20. |
| 061ж |
Нижний Новгород, "Буревестник" |
11.00. |
Фирм. |
Ежедневно |
04.40. |
06.20. |
| 115ж |
Нижний Новгород, "Буревестник" |
13.50. |
Фирм. |
Ежедневно |
04.55. |
08.55. |
| 117ж |
Нижний Новгород |
22.50. |
Скор. |
По нечётным |
06.20. |
16.30. |
| 265е |
Нижний Тагил (в Симферополь) |
20.29. |
Скор. |
Раз в неделю |
32.59. |
11.30. |
| 066д |
Николаев |
16.05. |
Скор. |
Ежедневно |
26.53. |
12.12. |
| 044с |
Новороссийск (в Санкт-Петербург), "Черноморец" |
02.50. |
Фирм. |
Ежедневно |
34.07. |
16.43. |
| 228а |
Новороссийск (в Санкт-Петербург) |
03.08. |
Скор. |
Дважды в неделю |
33.53. |
17.15. |
| 109м |
Новый Уренгой |
09.56. |
Скор. |
Ежедневно |
63.56. |
18.00. |
| 604м |
Орёл, "Орёл" |
06.14. |
Фирм. |
Кроме суббот |
07.14. |
23.00. |
| 263е |
Пермь (в Симферополь) |
20.29. |
Скор. |
По нечётным |
22.14. |
22.15. |
| 092п |
Полтава |
05.30. |
Скор. |
По чётным |
15.50. |
12.40. |
| 107й |
Самара (в Санкт-Петербург), "Самара" |
21.08. |
Скор. |
По чётным |
21.48. |
23.20. |
| 007а |
Санкт-Петербург (в Севастополь), "Нева" |
04.00. |
Скор. |
Ежедневно |
08.00. |
20.00. |
| 121а |
Санкт-Петербург (во Владикавказ) |
02.05. |
Скор. |
По чётным |
09.14. |
16.51. |
| 043с |
Санкт-Петербург (в Новороссийск), "Черноморец" |
23.35. |
Фирм. |
Ежедневно |
08.05. |
15.30. |
| 227а |
Санкт-Петербург (в Новороссийск) |
00.02. |
Скор. |
Дважды в неделю |
08.46. |
15.16. |
| 049а |
Санкт-Петербург (в Кисловодск) |
21.51. |
Скор. |
Ежедневно |
08.11. |
13.40. |
| 059а |
Санкт-Петербург (в Нижний Новгород), "Волга" |
01.40. |
Фирм. |
Ежедневно |
08.08. |
17.32. |
| 081м |
Санкт-Петербург (в Курск) |
02.26. |
Скор. |
По чётным |
07.37. |
18.49. |
| 107ж |
Санкт-Петербург (в Самару), "Самара" |
04.30. |
Фирм. |
По чётным |
07.50. |
20.40. |
| 131г |
Санкт-Петербург (в Ижевск) |
04.30. |
Скор. |
По нечётным |
07.50. |
20.40. |
| 143а |
Санкт-Петербург (в Харьков) |
22.03. |
Скор. |
По чётным |
08.15. |
13.48. |
| 147а |
Санкт-Петербург (в Мариуполь) |
21.20. |
Скор. |
По нечётным |
08.21. |
22.34. |
| 008п |
Севастополь (в Санкт-Петербург), "Нева" |
01.00. |
Скор. |
Ежедневно |
25.17. |
22.43. |
| 018п |
Севастополь |
19.42. |
Скор. |
Ежедневно |
25.37. |
17.05. |
| 204п |
Севастополь |
19.05. |
Скор. |
Ежедневно |
26.10. |
15.55. |
| 234п |
Севастополь |
21.53. |
Скор. |
Ежедневно |
25.44. |
19.09. |
| 030п |
Симферополь |
14.20. |
Фирм. |
Ежедневно |
22.39. |
14.41. |
| 068п |
Симферополь, "Крым" |
11.17. |
Фирм. |
Ежедневно |
22.05. |
12.12. |
| 208п |
Симферополь |
11.42. |
Скор. |
Ежедневно |
22.22. |
12.20. |
| 230п |
Симферополь |
23.27. |
Скор. |
Ежедневно |
23.03. |
23.24. |
| 264п |
Симферополь (в Пермь) |
03.33. |
Скор. |
По чётным |
24.46. |
01.47. |
| 266п |
Симферополь (в Нижний Тагил) |
03.33. |
Скор. |
По нечётным |
24.46. |
01.47. |
| 292д |
Симферополь |
20.18. |
Скор. |
Ежедневно |
24.15. |
19.03. |
| 284с |
Сочи |
06.04. |
Скор. |
Ежедневно |
39.32. |
14.32. |
| 020о |
Харьков, "Харьков" |
09.42. |
Фирм. |
Ежедневно |
12.47. |
19.55. |
| 144д |
Харьков (в Санкт-Петербург) |
01.17. |
Скор. |
По нечётным |
13.33. |
10.44. |
| 224к |
Феодосия |
17.06. |
Скор. |
Ежедневно |
26.42. |
13.24. |
Задачи на площади и периметры
Математический диктант.
Критерии оценки
математического диктанта – 1 правильный ответ – 10 баллов (максимальное количество баллов - 9)
Запишите формулы для вычисления площади
а) Квадрата;
б) Прямоугольника
в) Параллелограмма (через основание и высоту)
г) Параллелограмма (через стороны и синус угла)
д) Треугольника (через основание и высоту)
е) Треугольника (через стороны и синус угла)
ж) Треугольника (формула Герона)
з) Трапеции
и) Прямоугольного треугольника
Устные упражнения.
Критерии оценки
-1 правильный ответ – 10 баллов (максимальное количество баллов - 90)
1.Вычислите площадь фигур:

2.
Площадь 12 м2
: а) имеет один прямоугольник; б) имеют два прямоугольника; в) имеют три прямоугольника; г) имеют четыре прямоугольника.
Практическая работа
Критерии оценки
– 1 правильно решенная задача – 20 баллов (максимальное количество баллов - 60) + 10 баллов отвечающему у доски.
Задание № 1
На фотографии виден жилой дом, у которого крыша имеет форму пирамиды.
Ниже изображена математическая модель крышидома и указаны длины некоторых отрезков.На данной модели пол у чердака дома – квадрат ABCD. Балки, на которые опирается крыша, являются сторонами бетонного блока, имеющего форму прямоугольного параллелепипеда EFGHKLMN. E – середина ребра AT, F – середина BT, G - середина CT, H - середина DT. Все ребра пирамиды равны 12 м.
Хватит ли 30 кг краски для того чтобы покрасить пол чердака и крышу, если для покраски 1м2
требуется 100 г краски?
Задание № 2
В распоряжении детского сада имеется два прямоугольных участка. Один прямоугольный участок имеет длину 36м, а ширину 20м. Второй участок с длиной на 6 м меньше длины первого имеет ту же площадь. У садовника имеется 110 м забора. Какой из участков садовник сможет окружить забором?
Задание № 3
Финикийская царица Дидона спасалась от своего брата, тирана Пигмалиона. Она отплыла из города Тира в 825 году до нашей эры. После долгого путешествия корабль пристал к берегам Африки. Дидоне понравилась земля. Она обратилась к местному предводителю нумидийцев Ярбу с просьбой продать кусок земли. Ярб заломил баснословную цену за клочок земли, который можно окружить бычьей шкурой. Но Дидона не растерялась и согласилась. Она расплатилась и отправилась отмерять землю. Сначала она разрезала шкуру так, что получился тонкий кожаный ремешок длиной 18 км. Этим ремешком она окружила солидный участок земли, на котором обосновала впоследствии великий город Карфаген. Ярб был в ярости, так как его одурачили, но он был честным человеком и сдержал слово. Так гласит легенда. Но карфагенская цитадель называлась Бирса, что значит “бычья шкура”.
Определите наибольшую площадь, которую может занять Карфаген, если известно, что участок имеет форму:
a) Треугольника
b) Четырехугольника
c) Полуокружности
Самостоятельная работа
Критерии оценки
– 1 правильно решенная задача – 30 баллов (максимальное количество баллов - 60)
Задание № 1
Световая площадь окон в классе должна быть равна 1/5 площади пола. На складе имеется 3 вида краски:
a) Коричневая – 50 кг
b) Красная – 15 кг
c) Черная – 25 кг
Можно ли покрасить пол в 11 кабинетах равной площади краской одного цвета, если световая площадь окон равна 9,6 м?
Задание № 2
В магазине имеется два вида плиток для пола:
| Вид плитки |
Стоимость одной плитки |
| Квадратная плитка со стороной 2 дм |
12 р. |
| Плитка, площадь которой равна 1 кв. дм |
10 р. |
| Плитка, имеющая длину 3 дм и ширину 2 дм. |
15 р. |
В зале длиной 12 м и шириной 8 м нужно покрыть пол плитками. Какую плитку лучше приобрести, чтобы затраты на покрытие пола были минимальными?
Задачи для домашнего задания
Во время летних каникул Олег решил заработать денег не велосипед, который стоит 15000. ему предложили побелить фасад здания длиной 30 м и высотой 90 дм.
Сможет ли Олег без помощи родителей купить велосипед, если побелка стоит 80 руб. за 1 кв.м?
Подведение итогов
Накопительный лист учителя
| Ф.И.ученика |
Мат диктант |
Устная работа |
Практ.работа |
Самостоят.работа |
Итог |
Оценка |
|