Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Кафедра математического обеспечения и применения ЭВМ
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
по специальности: 010503 – Математическое обеспечение и администрирование информационных систем
на тему: «СИСТЕМЫ СЧИСЛЕНИЯ. СОСТАВЛЕНИЕ АЛГОРИТМОВ»
Руководитель работы М.Е. Щелкунова
Исполнитель Д.А. Кантимиров
2010
Задание
1.)
Заданы три числа А, В, С (таблица 1) соответственно в десятичном, двоичном и шестнадцатеричном виде. Каждое из этих чисел представить в двух других видах и в восьмеричном виде. А10=93. В2=1110001. С16=D5
а.) Организую перевод в двоичную систему счисления.
93:2=46 (1)
46:2=23 (0)
23:2=11 (1)
11:2=5 (1)
5:2=2 (1)
2:2=1 (0)
А2=01011101
Организую перевод в шестнадцатеричную систему счисления.
93:16=5 (D)
А16=5D
Организую перевод в восьмеричную систему счисления.
93:8=11 (5)
11:8= 1 (3)
А8=135
б.) В2=1110001
Организую перевод в десятичную систему счисления.
6543210 (нумерую числа по разрядам)
1110001
В10=1*2^6+1*2^5+1*2^4+1=64+32+16+1=11310
В10=113
Организую перевод в шестнадцатеричную систему счисления.
113:16=7 (1)
В16=71
Организую перевод в восьмеричную систему счисления.
113:8=14 (1)
14:18=1 (6)
В8=161
в.) С16= D5
Организую перевод в десятичную систему счисления.
1 0 (нумерую числа по разрядам)
D5
С10=13*16+5=213
С10=213
Организую перевод в двоичную систему счисления.
213:2=106 (1)
106:2=53 (0)
53:2=26 (1)
26:2=13 (0)
13:2=6 (1)
6:2=3 (0)
3:2=1 (1)
С2=0000000011010101 (т.к. 1 находящаяся на 8-ой позиции указывает на отрицательное число, в восьмиразрядную сетку число не влезает, буду работать в шестнадцатиразрядной)
Организую перевод в восьмеричную систему счисления
213:8=26 (5)
26:8=3 (2)
С8=325
2.
Используя числа, заданные в таблице 1, вычислить по правилам двоичной арифметики: А+ B, А - B, В - А, B - Cдля ЭВМ с длиной разрядной сетки, равной 8. Выполнить проверку (перевести результаты в десятичную систему счисления).
а.) А+В.
А2=01011101
В2=01110001
Произвожу операцию сложения столбиком
01011101
+
01110001
11001110 (так как результат в восьмиразрядную сетку число не влезает, буду работать в шестнадцатиразрядной)
А+В=00000000110011102
Проверка
Х=00000000110011102
Х10=1*2^7+1*2^6+1*2^3+1*2^2+1*2=128+64+8+4+2=206
А10+ В10=93+113=206
206=206 – верно
б.) А-В
А2=01011101
В2=01110001
Для того, чтобы вычитание заменить сложением, перевожу В в –В (инвертирую).
В2=01110001
Инвертирую
10001110
+
_______1
10001111
Произвожу операцию сложения А и –В.
01011101
+
10001111
11101100 (т.к 8 число является единицей, это указывает на то , что число отрицательное. Необходимо проводить инвертирование).
Инвертирую
00010011
+
_______1
-10100 ;
А-В=-10100
Проверка
А-В=-10100 ; А-В=-(1*2^4 + 1*2^2)=-20
А-В=93-113= -20
-20=-20 - верно
в.) В-А
А2=01011101
В2=01110001
Для того, чтобы вычитание заменить сложением, перевожу А в –А (инвертирую).
А2=01011101
Инвертирую
10100010
+
_______1
10100011
Произвожу операцию сложения -А и В.
01110001
+
10100011
100010100 (т.к. существует девятое число, то можно сделать вывод о логическом переполнении, следовательно от девятого знака необходимо избавиться.)
В-А=00010100
Проверка
В-А=00010100 ; В-А=1*2^4+1*2^2=20
В-А=113-93=20
20=20 – верно.
г.) В-С
С2=0000000011010101 (т.к. 1 находящаяся на 8-ой позиции указывает на отрицательное число, в восьмиразрядную сетку число не влезает, буду работать в шестнадцатиразрядной)
В2=0000000001110001
Для того, чтобы вычитание заменить сложением, перевожу С в –С (инвертирую).
С2=0000000011010101
Инвертирую
1111111100101010
+
_______________1
1111111100101011
Произвожу операцию сложения -С и В.
1111111100101011
+
0000000001110001
1111111110011100 (т.к 16 число является единицей, это указывает на то , что число отрицательное. Необходимо проводить инвертирование).
Инвертирую
0000000001100011
+
_______________1
-1100100 ;
В-С=-1100100
Проверка
В-С=-1100100; В-С=-(1*2^6+1*2^5+1*2^2)= -(64+32+4)=-100
В-С=113-213=-100
-100=-100 – верно.
3.)
Представить указанное в таблице число в четырехбайтовом IEEE формате.
А=345.867
Перевожу число в двоичную систему, при этом целая часть переводится отдельно от дробной.
Ι 345:2=172 (1)
172:2=86 (0)
86:2=43 (0)
43:2=21 (1)
21:2=10 (1)
10:2=5 (0)
5:2=2 (1)
2:2=1 (0)
34510=1010110012
ΙΙ 0.876*2=1.752 (1)
0.752*2=1.504 (1)
0.504*2=1.008 (1)
0.008*2=0.016 (0)
0.016*2=0.032 (0)
0.032*2=0.064 (0)
0.064*2=0.128 (0)
0.128*2=0.256 (0)
0.256*2=0.512 (0)
0.512*2=1.024 (1)
0.024*2=0.048 (0)
0.048*2=0,096 (0)
0.096*2=0.192 (0)
0.192*2=0.384 (0)
0.384*2=0.768 (0)
0.8672=111000000100000
Формирую число
А2=101011001.111000000100000
Привожу число к необходимому виду
А2=1.01011001111000000100000 *10-8
Работая с порядком десяти
P=127-8=11910
119:2=59 (1)
59:2=29 (1)
29:2=14 (1)
14:2=7 (0)
7:2=3 (1)
3:2=1 (1)
Р2=01110111
А2=1.01011001111000000100000*1001110111
2
Заполняю разрядную сетку IEEE формата
   А=00111011101011001111000000100000 А=00111011101011001111000000100000
Знак Степень Метиса
Ответ:00111011101011001111000000100000
4.)
Определить, попадает ли точка с произвольно заданными координатами (х, у) в заштрихованную область. Точки х, у задать самостоятельно.
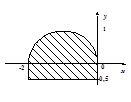
Задача сводится к нахождению пределов выделенной области. Для облегчения этой задачи я разделил график на две части.

Функция f1 лежащая выше оси Oy является формулой полуокружности, при у>0.
(x-x0)2
+(y-y0)2
≤r2
,
где r-радиус.
(x+1)+y2
≤1
y2
≤1-(x+1)2
y≤+ 2 2
Точка попадёт в область f1 при:
 у>0 у>0
y≤+ 2 2
Фигура f2 лежащая ниже оси Oy является прямоугольником, при y<0
Точка попадёт в область f1 при:
y≤0
 y>-0.5 y>-0.5
x≥-2
x≤0
Для упрощения алгоритма ввожу логические переменные , принимающие значения истина или ложь.
L1= y≤+ 2
и у>0 2
и у>0
L2= x≥-2 и x≤0 и y>-0.5 и y≤0
Блок-схема
 -+ -+
5.)
Пусть a1
=b1
=1; ak
= 3∙ bk
-1
+ 2∙ ak
-1
; bk
= 2∙ ak
-1
+ bk
-1
, k = 2,3, …
Дано натуральное число n. Вычислить

Задача сводится к накоплению суммы из выражений содержащих члены.
S=S+x , где ак и вк описываются как одномерные статистические массивы, а к! будет описан с помощью переменной F.
Первый член ряда равен:
X1=2/(1+1+1)*1=2/3
Цикл начинаю со второго элемента. Для избавления от бесконечного цикла, ввожу ограничение для предела к (n).
 - -

  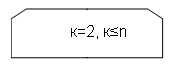
   
6.)
Разработать алгоритм обработки одномерных числовых массивов. Массивы задать самостоятельно, предусмотреть печать всех результатов.
В заданном одномерном массиве найти сумму и произведение положительных элементов, сумму и произведение отрицательных элементов. Из полученных результатов сформировать новый массив.
Пусть а-одномерный, числовой, динамический массиы.
S1- сумма положительных элементов
P1- произведение положительных элементов
S2- сумма отрицательных элементов
P2- произведение отрицательных элементов
z-одномерный, числовой, статистический массив, содержащий результаты.
 - -
  
    -+ -+
  
   
  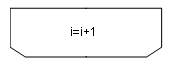
7.)
Разработать алгоритм обработки двумерных числовых массивов. Массивы задать самостоятельно, предусмотреть печать всех результатов.
В заданной действительной матрице размером  заменить элементы заменить элементы 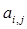 нулями, если нулями, если 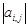 не равен не равен  , и 1 – в противном случае, где i – номер строки. , и 1 – в противном случае, где i – номер строки.
Пусть а(i,j)-динамический, двумерный числовой массив.
i-количество строк
j-количество столбцов
Задача сводится к нахождению максимального элемента в строке (max) и сравнения его с элементами данной строки.
 - -
   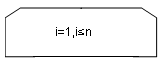 
   
    
  
+
   
    -+
 
 
|