Курсовая работа: Характеристика процесса исследования
|
Название: Характеристика процесса исследования Раздел: Рефераты по математике Тип: курсовая работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Введение Целью выполнения данной работы является овладение статистическими методами при изучении социальных и экономических явлений и процессов и приобретение навыков использования статистической информации при принятии управленческих решений. Для этого студенты пройдут последовательно все этапы статистического исследования, начиная с самостоятельной организации и проведения статистического наблюдения и заканчивая всесторонним анализом полученных данных. 1. Проведение статистического наблюдения Теоретико-методологический этап: Для проведениястатистического наблюдения была выбрана участковая больница. Целью наблюдения является количество населения, принимаемые данным учреждением за месяц. Задачи – определить число людей, обращающихся в больницу, провести обследование качества обслуживания, выявит отношение к платному лечению. Единицей наблюдения, как уже было указано выше, – участковая больница. Территорией наблюдения будет населенный пункт Кезского района Удмуртской Республики поселок Кузьма. Время наблюдения – один месяц. Программа наблюдения состоит из исследования качества обслуживания населения, количества людей, обращающихся за помощью в больницу. Вид наблюдения по времени проведения является единовременное. По охвату единиц – несплошное, разновидность несплошного – монографическое наблюдения. Способом наблюдения является документальное наблюдения и опрос. Вид опроса выбран саморегистрация. Организационный план: Органом наблюдения является автор данной курсовой работы. Данные собираются в течение месяца. Подготовительной работой будет разработка формы представления результатов исследования, разработка опросных листов для проведения саморегистрации. Данные листы содержат вопросы и место для ответа, некоторые вопросы будут содержать возможные варианты ответа. С инструкциями по заполнению население будет знакомиться устно. Примерные вопросы опросного листа: 1. Дата заполнения______________________________________________ 2. Возраст______________________________________________________ 3. Пол: М Ж (нужное подчеркнуть) 4. Социальное положение: работающий, пенсионер, учащийся, ребенок (нужное подчеркнуть) 5. Место жительства______________________________________________ 6. Удовлетворяет ли качество обслуживания? ________________________ 7. Пожелания по качеству обслуживания ____________________________ _______________________________________________________________________________________________________________________________________________________________________________________ 8. Отношение к платному лечению_________________________________ _______________________________________________________________________________________________________________________________________________________________________________________ 9. Согласны ли вы будете, если за некоторые виды лечения будет взиматься плата. Если нет, почему________________________________ _______________________________________________________________________________________________________________________________________________________________________________________ 10. Часто ли вы вызываете врача на дом? Отношение к обслуживанию _______________________________________________________________________________________________________________________________________________________________________________________ Контроль наблюдения необходим для выявления и устранения ошибок. В данном наблюдении может встретиться ошибка представительности. Для устранения этой ошибки проводится логический контроль. Ошибки будут исправляться лицом ответственным за наблюдение. 2. Группировка статистических данных Численность занятых в экономике по занятиям в 2009 году[1] (на конец ноября; тыс. чел.)
Группировочным признаком является численность людей, занятых в экономике. Так как признак количественный, следовательно, количество групп рассчитывается по формуле Стерджесса: n =1+3,322*lgN , где N – объем совокупности. Рассчитаем количество групп: n =1+3,322*lg28 = 5,821 ≈ 6, n = 6 Определяем интервал группировки. Т.к. вариация исходных данных большая, то интервалы будут равные и закрытые, поэтому их величину определяем по формуле:
где Xmax – наибольшее значение признака совокупности, Xmin – наименьшее значение признака совокупности, n – количество групп в группировке. Рассчитаем интервалы группировки:
Единицы совокупности распределяются по группам
На основании полученных данных построим группировочную таблицу, учитывая, что округление интервала производилось в сторону увеличения, то нижняя граница последнего интервала будет больше чем наибольшее значение исходных данных:
3. Расчет характеристик вариационного ряда По полученной группировке построим вариационный ряд, рассчитаем показатели центра распределения и показатели вариации распределения. Т.к. группировка строилась по количественному признаку, то получим вариационный ряд. Он состоит из вариант (отдельные значения варьируемого признака в совокупности) и частот (количество единиц совокупности с данным значением признака). К показателям центра распределения относятся средняя арифметическая, мода, медиана. Средняя арифметическая рассчитывается по формуле:
где m – количество групп; xj – варианты; fj – частоты. В интервальных рядах вместо вариант xj
используется середина интервала Найдем середину каждого из интервалов. Она находится по формуле:
где x верх – верхняя граница интервала; x ниж – нижняя граница интервала. Рассчитаем середину каждого интервала:
Рассчитаем среднюю арифметическую:
Таким образом, 2572 тыс. чел. – наиболее характерное значение численности населения, занятого в экономике. Следующим показателем центра распределения является мода. В интервальных рядах по наибольшей частоте определяется модальный интервал, а затем рассчитывается мода по формуле:
где X 0 - нижняя граница модального интервала; f Mo – частота модального интервала; f Mo-1 – частота предмодального интервала; f Mo+1 – частота послемодального интервала; i – величина модального интервала. Модальным интервалом является первая группа в группировочной таблице. Рассчитаем моду:
Таким образом, значение 505 тыс. чел. – наиболее часто встречаемое среди занятых в экономике. Далее находим медиану. В интервальных рядах медиана равна варианте, накопленная частота которой больше либо равна половине объема совокупности (f
/
Me
где X 0 – нижняя граница медианного интервала; f Me-1 / – накопленная частота предмедианного интервала; f Me – частота медианного интервала; i – величина медианного интервала. Половина объема совокупности равна 14 (
Половина из обследованных признаков меньше 2223 тыс. чел., а другая половина больше. Теперь рассчитаем показатели центра распределения. К ним относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия, коэффициент вариации. Размах вариации рассчитывается по формуле:
где Рассчитаем размах вариации:
Среднее линейное отклонение рассчитывается как средняя арифметическая из модулей отклонений вариант от средней. Т.к. данные сгруппированы, то рассчитывается среднее линейное отклонение взвешенное:
где xj
– варианты;f
j
– частоты; Рассчитаем среднее линейное отклонение взвешенное:
Среднее квадратическое отклонение рассчитывается как корень из средней арифметической квадратов отклонений от средней. По сгруппированным данным рассчитывается среднее квадратическое отклонение взвешенное:
где m
– количество групп; x
/
j
– середина j
-го интервала; Рассчитаем седнее квадратическое отклонение взвешенное:
На 1667 и на 1925 тыс. чел. в среднем отличаются отдельные значения совокупности от средней численности занятых в экономике. Взвешенная дисперсия рассчитывается по формуле:
где Рассчитаем взвешенную дисперсию:
Найдем типичность средней величины через коэффициент вариации:
где Рассчитаем данный показатель:
Так как коэффициент > 40%, следовательно, средняя нетипична, а исследуемая совокупность неоднородна. 4. Анализ связи между признаками по аналитической группировке Денежные доходы и потребительские расходы в расчете на душу населения(рублей)
По имеющимся данным определим признак-фактор и признак-результат. Признак-фактор – денежные доходы, признак-результат – потребительские расходы. Построим группировку по признаку-фактору. Для этого определим количество групп и величину интервалов по вышеприведенным формулам. Количество групп возьмем равной 5
На основании полученных данных построим группировочную таблицу:
В каждой группе рассчитаем среднее значение результативного признака как простую среднюю арифметическую из значений результативного признака у всех единиц совокупности, входящих в данную группу. Она рассчитывается по формуле:
где yj – значение результативного признака в группе; n – количество единиц в группе.
Аналитическая группировочная таблица
По полученным данным проведем дисперсионный анализ и определим характер связи. В анализе рассчитываются три вида дисперсии: межгрупповая, средняя внутригрупповая, общая. Межгрупповая дисперсия рассчитывается по формуле:
где
8976355,22 рублей – вариация потребительских расходов под влиянием денежных доходов. Для расчета средней внутригрупповой дисперсии сначала находится внутригрупповые дисперсии по каждой группе аналитической группировки:
где yij
– отдельные значения результативного признака в j
-й группе; Рассчитаем внутригрупповые дисперсии:
Средняя внутригрупповая дисперсия:
где
547342,2 – случайная вариация потребительских расходов, возникающая под влиянием денежных доходов. Общая дисперсия находится по формуле:
где Рассчитаем общую дисперсию:
Мерой тесноты связи между результативным и факторным признаками является коэффициент детерминации:
Рассчитаем коэффициент детерминации:
0,94 – эта часть общей вариации потребительских расходов объясняется денежными доходами. Эмпирическое корреляционное отношение показывает тесноту связи:
Рассчитаем данный показатель:
Определяем показатель силы связи:
где Для этого определим середины первой и последней групп, по вышеприведенным формулам:
Рассчитаем силу связи:
Из данного показателя следует, что сила связи прямая, т.е. при увеличении денежных доходов на 1 рубль происходит увеличение потребительских расходов на 0,71 рубль. 5. Корреляционно-регрессионный анализ Данный анализ проведем на основании данных, приведенных в задании 4.4.
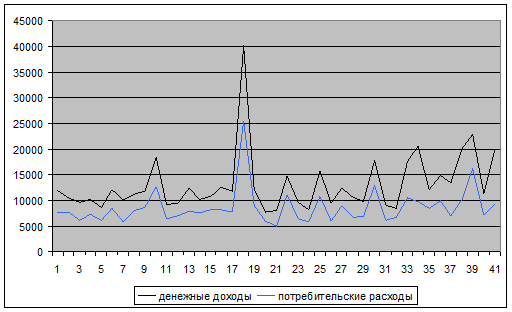
Изобразим связь между данными признаками графически:
Исследуется парная линейная корреляция:
Рассчитаем параметры a иb :
Промежуточные расчеты приводим в таблице:
Рассчитаем параметры уравнения:
Составим уравнение парной линейной корреляции:
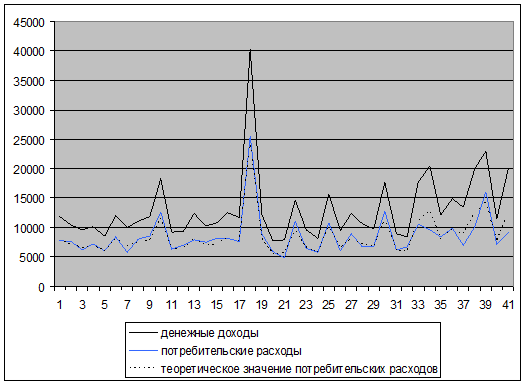
Составим график теоретического значения потребительских расходов:
Найдем тесноту связи между денежными доходами и потребительскими расходами:
Рассчитаем данный показатель:
Рассчитаем коэффициент детерминации:
Т.о. связь между потребительскими расходами и денежными доходами весьма тесная, изменение потребительских расходов на 90% зависит от денежных доходов населения. 6. Анализ рядов динамики Численность постоянного населения на 1 января, человек, на 1 января
По приведенным данным рассчитаем основные характеристики интервального ряда динамики: наблюдение статистический группировка вариационный
Средние характеристики интервального ряда динамики определяется по формуле: Средний уровень ряда:
где По данным формулам рассчитаем показатели: Абсолютный прирост цепной:
Абсолютный прирост базисный:
Темп роста цепной:
Темп роста базисный:
Темп прироста цепной:
Темп прироста базисный:
Аналогично рассчитываются показатели за другие года. При этом, цепные показатели имеют переменную базу сравнения, а базисные – постоянную – 2001 года. В таблице приведены рассчитанные показатели:
Далее найдем средний уровень интервального ряда по формуле:
где yi – уровни ряда; n – количество уровней в ряду. Рассчитаем данный показатель:
Проанализировав полученные данные можно сказать, что численность постоянного населения в Удмуртии на протяжении 10 лет постепенно снижается. По сравнению с 2001 годом, в 2010 году уменьшение численности достигло на данный момент наибольшего значения – 68673 человека. Темп роста цепной показывает, на сколько изменилась численность населения по сравнению с предыдущим годом. В среднем численность уменьшается на 0,05 долей. А уменьшение данного показателя по сравнению с 2001 годом варьируется от 0,04 до 0,5. В данном случае цепной темп прироста показывает уменьшение абсолютного прироста относительно численности населения в разные годы (от 0,006 до 0,003). А базисный – относительно 2001 года. Это уменьшение варьируется от 0,006 до 0,09. Произведем сглаживание ряда с помощью скользящей средней. Для этого установим звенья скользящей средней – 3. Теперь рассчитаем средние уровни в каждом звене по формулам:
Т.к. в звене нечетное количество элементов, то можно определить тенденцию по ряду скользящих средних. Для этого построим график и нанесем на него полученный тренд. Произведем сглаживание ряда динамики с помощью аналитического выравнивания по адекватной функции. В данном методе тенденция рассматривается как функция от времени:
Промежуточные расчеты приведены в таблице:
Теперь рассчитаем необходимые параметры:
Подставив полученные параметры в уравнение функции, найдем, тенденцию и представим ее на графике: Из проведенного анализа можно сделать вывод о том, что численность населения имеет тенденцию к постепенному увеличению. 7. Индексы Динамика реализации овощей на рынках города в 2010 году
Рассчитаем цепные индексы, проверим правильность расчетов индексов, используя их взаимосвязь, рассчитаем сводные индексы цен и физических объемов с постоянными и переменными весами, сделаем выводы об изменении исследуемых показателей. Индивидуальные цепные индексы рассчитываются по формулам:
Для проверки правильности расчета найдем индивидуальные базисные индексы цены:
Приведем пример расчета по одному из этих показателей, остальные приведем в таблице:
Проверка основана на связи индексов: произведение цепных индексов дает базисный индекс последнего периода. Рассчитаем сводные индексы цен и физического объема. Общие цепные индексы цены:
Общие базисные индексы цены:
Общие цепные индексы физического объема:
Общие базисные индексы физического объема:
Рассчитаем по одному из индексов, а остальные приведем в таблице:
Анализируя индивидуальные цепные индексы можно сделать следующие выводы. Цена на картофель в феврале уменьшилась на 0,25% по сравнению с ценами в январе. А цены на капусту, лук, свёклу, морковь растут на 68,98%, 64,24%, 26,25% и 68,92% соответственно. В марте цены, по сравнению с февральскими ценами, на данную продукцию уменьшились, в апреле снова поднялись в сравнении с мартом, а в мае снова упали. Анализируя базисные индексы цен, можно сказать, что на картофель цена имеет тенденцию к снижению по сравнению с ценами января. На остальную сельскохозяйственную продукцию – к увеличению. Общие цепные индексы цены показывают изменение стоимости товаров в данном месяце по сравнению с ценами предыдущего месяца и объемом продаж данного месяца. В феврале, например, стоимость товаров увеличилась на 15,21%, в марте уменьшилась на 11,24%, в апреле увеличилась на 7,62%, в мае снова снизилась на 11,23%. Общие базисные индексы цены показывают изменение стоимости товаров в данном месяце по сравнению с ценами января и объемом продаж в данном месяце. Так, в феврале и апреле данный индекс увеличился на 15,21% и 8,92% соответственно, в марте и мае уменьшился на 0,02% и 14,3% соответственно. Общие цепные индексы физического объема показывают изменение товарооборота в данном месяце и цены января по сравнению с ценами января и объемам продаж в предыдущем месяце. По данной таблице видно, что в феврале, марте и мае этот индекс уменьшился на 53,58%, 13,2% и 9,75% соответственно. А в апреле – увеличился на 5,16%. Общие базисные индексы физического объема показывают изменение товарооборота в данном месяце и цены января по сравнению с ценами и объемом продаж в январе. Данный показатель на протяжении всех исследуемых месяцев уменьшаются на 53,58% в феврале, на 40,2% в марте, на 57,63% в апреле и 61,76% в мае. Список использованной литературы 1. Методические указания по выполнению курсовой работы по дисциплине «Статистика» – Глазов, 2006. – 32 с. 2. www.gks.ru [1]
По данным выборочного обследования населения по проблемам занятости. Данные приведены по основному или единственному месту работы. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
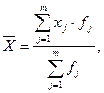
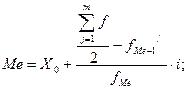
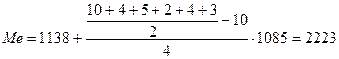
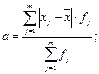
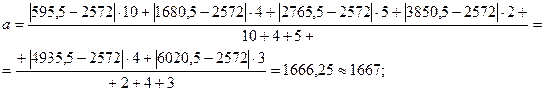
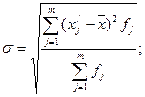
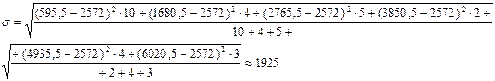
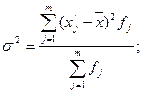
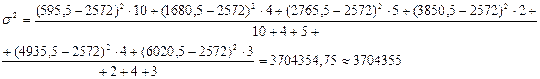
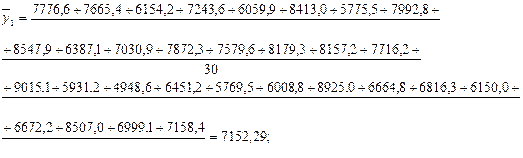
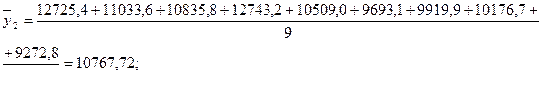
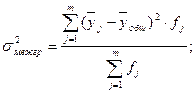
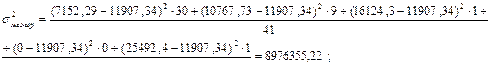
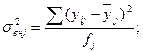
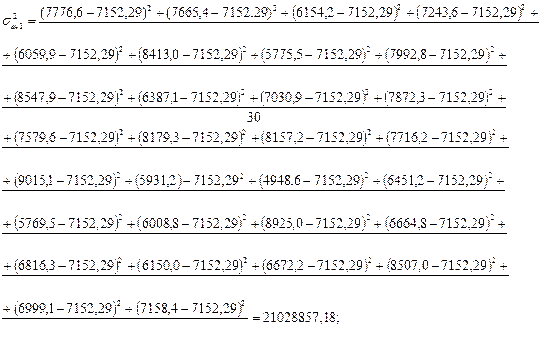
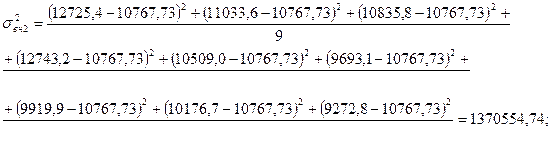
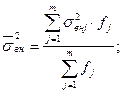
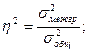
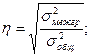

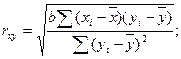
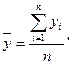 ,
,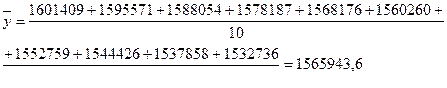
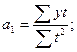
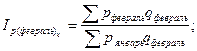
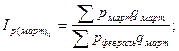
 и т.д.
и т.д.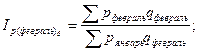
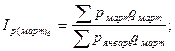
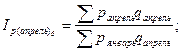 и т.д.
и т.д.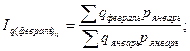
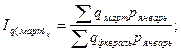
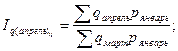 и т.д.
и т.д.