Часть
I
. Синтез управляющих устройств
Исходные данные
На рисунке приведена структурная схема последовательного соединения исполнительного механизма и объекта управления.
В качестве исполнительного механизма используется механизм постоянной скорости с ограничением:
Объект управления описывается передаточными функциями вида:
Численные значения параметров исполнительного механизма и объекта управления:
| Вариант |
kим
|
k1
|
k2
|
T1
|
T2
|
x1
|
x2
|
| 11 |
0,20 |
1,00 |
1,00 |
1,80 |
3,80 |
0,80 |
0,80 |
Задание:
Провести анализ динамических свойств объекта управления с использованием графиков переходного процесса и АЧХ. При определении длительности переходного процесса принять в = ±5% от установившегося значения выходной переменной.
Для моделирования системы управления используем программу МВТУ (моделирование в технических устройствах).

Рис.1 – Объект управления

Рис.2 – График переходного процесса
По графику видно, что система является устойчивой с плавным переходным процессом без перерегулирования. Установившееся значение выходной переменной составляет 1. Из списка значений графика можно определить, что максимальное значение составляет 1.01547. Время переходного процесса составляет 15.99 с.

Рис.3 – График АЧХ
АЧХ показывает, во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на всём диапазоне.
А
max
= A0
= 1;
Частота среза
: A = 0.01 ω
c
= 0,0551;
Полоса пропускания
: A = 0.707 ωп
= 0,6316.
2 РАЗРАБОТКА ЛИНЕЙНОГО РЕГУЛЯТОРА
Параметры ступенчатого входного воздействия:
1) время «включения» скачка t = 0;
2) значение сигнала до скачка Y0
= 0;
3) значение сигнала после скачка Yk
= 40.
На рисунке 2.1 изображена схема последовательно соединённых исполнительного механизма и объекта управления, на которые подаётся ступенчатое входное воздействие.

Рисунок 2.1 - Схема последовательно соединённых исполнительного механизма и объекта управления.
График переходного процесса, протекающего в системе управления, изображён на рисунке 2.2.

Рисунок 2.2 – Переходной процесс
В заданной схеме 2.1 исполнительный механизм представляет собой интегратор с ограничениями. Поэтому при выборе регулятора необходимо учитывать, что интегральная составляющая в схеме уже присутствует.
Существует два вида регуляторов без интегральной составляющей: П-регулятор и ПД-регулятор. Добавка П-регулятора в систему управления делает её высокоточной в установившемся режиме, но в переходном режиме качество системы ухудшается. Передаточная функция П-регулятора:
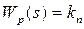 . .
Её соединение с передаточной функцией исполнительного механизма даст:
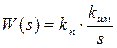 . .
Соединение пропорциональной и интегральной составляющих увеличит точность системы управления.
ПД-регулятор улучшает качество системы в переходном режиме, на качество системы в установившемся режиме влияет слабо. Передаточная функция ПД-регулятора:
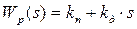 . .
Её соединение с передаточной функцией исполнительного механизма даст:
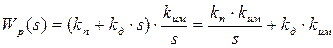 . .
Соединение пропорциональной и интегральной составляющих увеличит точность системы управления, а соединение дифференциальной и интегральной составляющих увеличит быстродействие системы.
Необходимо получить быстрый переходной процесс без перерегулирования, следовательно, наиболее подходящим для этого является ПД-регулятор. Схема линейного регулятора в системе управления изображена на рисунке 2.3.

Рисунок 2.3 – Схема с линейным регулятором
3 РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРА
Для определения численных значений параметров линейного регулятора воспользуемся методом Циглера –Никольса.
Регулятор управляет объектом с такой передаточной функцией:
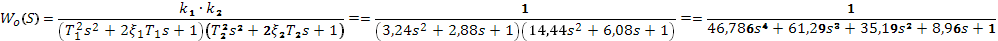
Передаточная функция разомкнутой системы:
Далее используем критерий Найквиста:
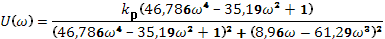
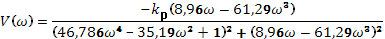
Необходимо довести систему до границы устойчивости
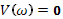
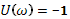
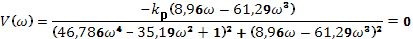
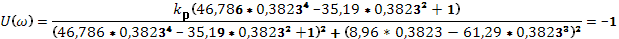

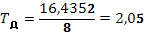
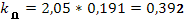
Исходя из передаточной функции ПД-регулятора для данного проектирования, Wр
(S)=kp
(1+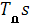 ), параметры регулятора ), параметры регулятора
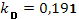
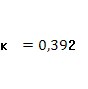
При найденных параметрах получаем переходной процесс без перерегулирования, изображенный на рис. 3.2. Время переходного процесса – 62с.

Рисунок 3.2 – График переходного процесса при выбранных параметрах базового регулятора.
4 АНАЛИЗ ДИНАМИЧЕСКИХ СВОЙСТВ САУ
Проведём анализ динамических свойств САУ, синтезированной в первой части расчетной работы, при k
2
= 0,4. График переходного процесса изображен на рисунке 4.1.

Рисунок 4.1 – График переходного процесса
Процесс проходит плавно, без перерегулирования, время переходного процесса t = 129 c.
Проведём анализ динамических свойств САУ, синтезированной в первой части расчетной работы, при k
2
= 1,6. График переходного процесса изображен на рисунке 4.2.

Рисунок 4.2 – График переходного процесса
Процесс колебательный, с перерегулированием. Время переходного процесса t = 23 c.
Перерегулирование σ = 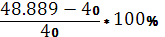 = 22,2225%. = 22,2225%.
Проведем анализ САУ при случайном изменении коэффициента усиления k
1
(при k
2
= 1,0) в виде нормального шума с математическим ожиданием, равным m
k
= 1,0, и дисперсией, равной D
k
= 0,2. Схема модели представлена на рисунке 4.3.

Рисунок 4.3 – Схема модели с использованием блока «Нормальный шум»

Рисунок 4.4 – График нормального шума
График переходного процесса изображен на рисунке 4.4. Время переходного процесса t = 35 c.

Рисунок 4.4 – График переходного процесса.
5 ФОРМИРОВАНИЕ ЭТАЛОННОЙ МОДЕЛИ САУ
В качестве эталонной модели возьмем апериодическое звено 2-го порядка с передаточной функцией
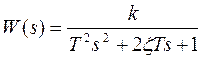 . .
Значение параметров эталонной модели:
k=1 – усиливает или уменьшает сигнал;
T=5.5 – влияет на скорость переходного процесса;
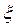 =0.75. =0.75.
Схема с эталонной моделью представлена на рисунке 5.1. На рисунке 5.2 изображены переходные процессы моделей. Время переходного процесса эталонной модели t = 20.2c.

Рисунок 5.1 – Схема эталонной и реальной моделей.

Рисунок 5.2 – Графики переходных процессов моделей.
6 СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЭТАЛОННОЙ МОДЕЛИ И РЕАЛЬНОЙ САУ
Среднеквадратическая ошибка вычисляется по формуле:
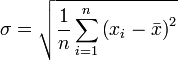
Для вычисления СКО в структуру модели добавлен микроблок, реализующий данную формулу:
Описание микроблока: в блок поступают 2 сигнала – с реальной и эталонной моделей, затем берется их разность и модуль числа, чтобы не было отрицательных значений. Затем, согласно формуле заданы возведение в квадрат и квадратный корень. Блок «Ключ интегратора» определяет значение времени, в течении которого определяется ошибка. Коэффициент усиления определяет количество точек.

Рисунок 6.1 – Структура блока СКО.
На выходе блока стоит график, показывающий значение СКО в каждый момент времени. На рисунке 6.2 приведено значение СКО при k2
= 1.

Рисунок 6.2 – Значение СКО при k
2
= 1.
При k
2
= 0,4 вид переходного процесса реальной модели показан на рисунках 6.3. СКО составляет σ = 3,6237 (рисунок 6.4).

Рисунок 6.3 – График переходного процесса при k
2
= 0,4.

Рисунок 6.4 – График СКО реальной модели при k
2
= 0,4.
При k
2
= 1,6 переходной процесс имеет следующий вид (рисунок 6.5). СКО составляет σ = 3,052 (рисунок 6.6).

Рисунок 6.5 - График переходного процесса при k
2
= 1,6.

Рисунок 6.6 – График СКО реальной модели при k
2
= 1,6.
7 СИНТЕЗ АДАПТИВНОЙ САУ С ЭТАЛОННОЙ МОДЕЛЬЮ
Основной задачей адаптивного контура является поддержание сигнала на заданной уровне при параметрическом возмущении. Было установлено, что при изменении в объекте k
2
изменяется и переходной процесс.
При k
2
= 0,4 переходной процесс протекает достаточно долго, следовательно в адаптивном контуре мы должны уменьшить его время.
При k
2
= 1,6 в переходном процессе появляется колебания, следовательно необходимо их погасить.
Добавим в модель график (рисунок 7.1) и посмотрим значение разницы между сигналами реальной и эталонной моделей и изменении k
2
в объекте.

Рисунок 7.1 – Схема модели.
Поменяем значение k
2
на 0,4, а затем на 1,6 и проанализируем изменение разницы 2-х сигналов. На рисунке 7.2 видим, что разница сигналов при k
2
= 0,4 принимает отрицательные значения, а при k
2
= 1,6 (рисунок 7.3) значения разницы положительные и отрицательные. Следовательно при построении адаптивного контура необходимо учитывать значения разницы 2-х сигналов и соответственно реагировать на её изменении. В адаптивном контуре будет две параллельных ветви, которые при изменении знака разницы 2-х сигналов будут реагировать на изменение k
2
в объекте. Для переключения между ветвями используем ключ 2А.

Рисунок 7.2 – значение разницы сигналов при k
2
= 0,4.

Рисунок 7.3 – значение разницы сигналов при k
2
= 1,6.
Для ветви, реагирующей на k
2
= 0.4 построим следующую структуру. Когда значение разницы 2-х сигналов станет отрицательным, пропускаем его через усилитель с зоной нечувствительности, равной 3σ. Это дает возможность увеличить отрицательный сигнал, выходящий за 3σ-зону и не реагировать на малые значения сигнала. Затем усилителем увеличиваем разницу сигналов, чтобы переходной процесс ОУ совпадал с эталонной моделью. После прохождения этой ветви сигнал должен быть отрицательным.
Для ветви, реагирующей на k
2
= 1.6, структуру постоем иначе. Когда значение разницы 2-х сигналов станет положительным, ключ пропустит его на вторую ветвь. Т.к. k
2
= 1.6 в системе появляются колебания, то с помощью производной уменьшаем их. Затем апериодическим звеном первого порядка сглаживаем оставшиеся колебания и уменьшаем время. После прохождения апериодического звена первого порядка сигнал принимает отрицательные и положительные значения. Необходимо на выходе из второй ветви получить только положительные значения сигнала, поэтому излом пропустит только положительный сигнал.
Схема адаптивного контура представлена на рисунке 7.4.

Рисунок 7.4 – Схема адаптивного контура.
Параметры используемых блоков:
1) усилитель с зоной нечувствительности: a = -3.1, b = 3.1, k = 1;
2) усилительkx: k=8;
3) апериодическое звено I порядка:k = 5, T = 0.001;
4) излом: k1
= 0, k2
= 1.8.
Графики переходных процессов при k
2
= 1, k
2
= 0,4 и k
2
= 1,6 изображены на рисунках 7.5, 7.7 и 7.9 соответственно. При k
2
= 1 СКО равно 0.114, при k
2
= 0,4 СКО равно 2.63, при k
2
= 1.6 СКО равно 2.2.

Рисунок 7.5 - График переходного процесса при k
2
= 1.

Рисунок 7.6 – график СКО при k
2
= 1.

Рисунок 7.7 - График переходного процесса при k
2
= 0,4.

Рисунок 7.8 – график СКО при k
2
= 0,4.

Рисунок 7.9 - График переходного процесса при k
2
= 1,6.

Рисунок 7.10 – график СКО при k
2
= 1,6.
Вывод:
В первой части расчетной работы я провел анализ динамических свойств заданного объекта управления и сконструировал линейный регулятор, обеспечивающий перевод объекта из начального состояния в конечное. Также методом незатухающих колебаний Циглера-Никольса были рассчитаны параметры линейного регулятора.
В ходе выполнения второй части работы - «Синтез адаптивной САУ с эталонной моделью», был проведен анализ динамических свойств САУ, синтезированной в первой части работы. Был проведен сравнительный анализ реальной и эталонной модели, при использовании различных коэффициентов и проверка среднеквадратической ошибки. Также выбрана эталонная модель.
В итоге была сформирована адаптивная САУ, которая поддерживает уровень сигнала на заданном уровне, причем в адаптивной системе среднеквадратическое отклонение уменьшается почти в два раза, соответственно и погрешность уменьшилась.
|