Министерство общего и профессионального образования РФ
Южно-Уральский Государственный Университет
Кафедра «Системы управления»
КУРСОВАЯ РАБОТА
ПО ИССЛЕДОВАНИЮ ОПЕРАЦИЙ
Вариант 14
Группа ПС-317
Выполнил: Родионова Е.В.
Проверил: Плотникова Н.В.
Челябинск, 2004
Содержание
Задача 1 2
Задача 2 4
Задача 3 6
Задача 4 8
Задача 1
№14
Условие:
Нефтеперерабатывающий завод получает 4 полуфабриката: x1 тыс. л. алкилата, x2 тыс. л. крекинг-бензина, x3 тыс. л. бензина прямой перегонки и x4 тыс. л. изопентана. В результате смешивания этих четырех компонентов в разных пропорциях образуется три сорта авиационного бензина: бензин А (а1:а2:а3:а4), бензин В (b1:b2:b3:b4) и бензин С (с1:с2:с3:с4).
Стоимость 1 тыс. л. бензина каждого сорта равна y1 руб., y2 руб. и y3 руб.
Определить соотношение компонентов, при котором будет достигнута максимальная стоимость всей продукции.
| № вар. |
x1 |
x2 |
x3 |
x4 |
y1 |
y2 |
y3 |
а1 |
а2 |
а3 |
а4 |
b1 |
b2 |
| 1 |
400 |
250 |
350 |
100 |
120 |
100 |
150 |
2 |
3 |
5 |
2 |
3 |
1 |
| № вар. |
b1 |
b2 |
c1 |
c2 |
c3 |
c4 |
| 1 |
2 |
1 |
2 |
2 |
1 |
3 |
Решение:
Составим математическую модель задачи.
Обозначим через t1 количество бензина А;
через t2 количество бензина В;
через t3 количество бензина С.
Тогда, целевая функция будет
L=y1t1+ y2t2+ y3t3=120t1+100t2+150t3 →max
Система ограничений:
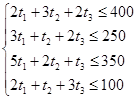
Приведем систему ограничений к виду основной задачи линейного программирования (введем новые переменные t4 , t5 ,t6 ,t7, которые входят в целевую функцию с нулевыми коэффициентами):
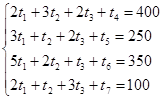
Выберем t1 , t2 ,t3 свободными переменными, а t4 , t5 ,t6 ,t7 – базисными и приведем к стандартному виду для решения с помощью симплекс-таблицы:
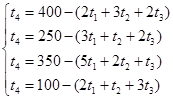
L=0-(-120t1-100t2-150t3)
Составим симплекс-таблицу.
Это решение опорное, т.к. все свободные члены положительны.
Т. к. все коэффициенты в целевой функции отрицательные, то можно взять любой столбец разрешающим (пусть t1). Выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это t7)
| b |
t1 |
t2 |
t3 |
| L |
0 |
-120 |
-100 |
-150 |
| 6000 |
60 |
60 |
180 |
| t4 |
400 |
2 |
3 |
2 |
400/2=200 |
| -100 |
-1 |
-1 |
-3 |
| t5 |
250 |
3 |
1 |
2 |
250/3=83,3 |
| -150 |
-1,5 |
-1,5 |
-4,5 |
| t6 |
350 |
5 |
2 |
1 |
350/5=70 |
| -250 |
-2,5 |
-2,5 |
-7,5 |
| t7 |
100 |
2 |
1 |
3 |
100/2=50 |
| 50 |
0,5 |
0,5 |
1,5 |
Далее меняем t2 и t1 .
| b |
t7 |
t2 |
t3 |
| L |
6000 |
60 |
-40 |
30 |
| 4000 |
40 |
80 |
120 |
| t4 |
300 |
-1 |
2 |
-1 |
300/2=150 |
| -200 |
-2 |
-4 |
-6 |
| t5 |
100 |
-1,5 |
-0,5 |
-2,5 |
| 50 |
0,5 |
1 |
-4,5 |
| t6 |
50 |
-2,5 |
-0,5 |
-6,5 |
| 50 |
0,5 |
1 |
-7,5 |
| t1 |
50 |
0,5 |
0,5 |
1,5 |
50/0,5=100 |
| 100 |
1 |
2 |
1,5 |
| b |
t7 |
t1 |
t3 |
| L |
10000 |
100 |
80 |
150 |
| t4 |
100 |
-3 |
-4 |
-7 |
| t5 |
150 |
-1 |
1 |
-1 |
| t6 |
100 |
-2 |
1 |
-5 |
| t2 |
100 |
1 |
2 |
3 |
Т.к. коэффициенты при переменных в целевой функции положительны, следовательно, это оптимальное решение.
Таким образом, t1 = t3 =0; t2=100; L=10000.
Т.е. для получения максимальной прибыли следует производить только бензин В (100 тыс. л.), при этом выручка составит 10000 руб.
ОТВЕТ: для получения максимальной прибыли следует производить только бензин В (100 тыс. л.), при этом выручка составит 10000 руб.
Задача 2
№34
Условие:
С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции Q=CTx при условии Ax ³£B,
где CT = [c1 c2 . . . c6 ]T , ВT = [ b1 b2 . . . b6 ]T ,
XT = [x1 x2 . . . x6]T , А= [aij] (i=1,6; j=1,3).
| № вар. |
с1 |
с2 |
с3 |
с4 |
с5 |
с6 |
b1 |
b2 |
b3 |
Знаки ограничений |
a11 |
a12 |
a13 |
a14 |
| 1 |
2 |
3 |
| 34 |
3 |
3 |
1 |
1 |
0 |
0 |
4 |
4 |
15 |
= |
= |
= |
2 |
0 |
3 |
1 |
| № вар. |
a15 |
a16 |
a21 |
a22 |
a23 |
a24 |
a25 |
a26 |
a31 |
a32 |
a33 |
a34 |
a35 |
a36 |
Тип экстрем. |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1. 34 |
0 |
0 |
1 |
0 |
–1 |
2 |
3 |
0 |
3 |
3 |
6 |
3 |
6 |
0 |
max |
Решение:
Исходная система:
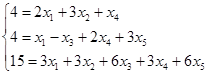
Целевая функция Q= x1+3x2+x3+3x5.
Пусть х3, х4 – свободные переменные, х1, х2, х5 – базисные.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
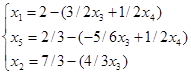
Q=9 - (9/2x3-1/2x4)
Составим симплекс-таблицу:
| b |
x3 |
x4 |
| Q |
9 |
9/2 |
-1/2 |
| 2/3 |
-5/6 |
1 |
| x1 |
2 |
3/2 |
1/2 |
2/0,5=4 |
| -2/3 |
5/6 |
-1 |
| x2 |
7/3 |
4/3 |
0 |
| 0 |
0 |
0 |
| x5 |
2/3 |
-5/6 |
1/2 |
2/3 : 1/2=4/3 |
| 4/3 |
-5/3 |
2 |
Это опорное решение, т.к. свободные члены положительны.
Т.к. коэффициент при х4 отрицательный, то это и будет разрешающий столбец. В качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это х5).
| b |
x3 |
x5 |
| Q |
29/3 |
11/3 |
1 |
| x1 |
4/3 |
2/3 |
-1 |
| x2 |
7/3 |
4/3 |
0 |
| x4 |
4/3 |
-5/3 |
2 |
Т.к. коэффициенты при переменных в целевой функции положительны, следовательно, это оптимальное решение.
Т. о. Q=29/3
x3=x5=0; x1=4/3; x2=7/3; x4=4/3.
ОТВЕТ: Q=29/3ж
x3=x5=0; x1=4/3; x2=7/3; x4=4/3.
Задача 3
№14
Условие:
Решение транспортной задачи:
1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
| №вар. |
а1 |
а2 |
а3 |
b1 |
b2 |
b3 |
b4 |
b5 |
с11 |
с12 |
с13 |
| 14 |
90 |
50 |
30 |
15 |
45 |
45 |
50 |
15 |
45 |
60 |
40 |
| с14 |
с15 |
с21 |
с22 |
с23 |
с24 |
с25 |
с31 |
с32 |
с33 |
с34 |
с35 |
| 60 |
95 |
35 |
30 |
55 |
30 |
40 |
50 |
40 |
35 |
30 |
100 |
Решение:
Составим таблицу транспортной задачи и заполним ее методом северо-западного угла:
| B1 |
B2 |
B3 |
B4 |
B5 |
a |
| A1 |
45 |
60 |
40 |
60 |
95 |
90 |
| 15 |
45 |
30 |
| A2 |
35 |
30 |
55 |
30 |
40 |
50 |
| 15 |
35 |
| A3 |
50 |
40 |
35 |
30 |
100 |
30 |
| 15 |
15 |
| b |
15 |
45 |
45 |
50 |
15 |
170 |
Это будет опорный план.
Количество заполненных ячеек r=m+n-1=6.
1) Рассмотрим цикл (1,2)-(1,3)-(2,3)-(3,2):
с1,2+с2,3>c1.3+c3.2 (60+55>30+40)
Количество единиц товара, перемещаемых по циклу: min (с1,2 ; с2,3)=15
2) Рассмотрим цикл (2,4)-(2,5)-(3,5)-(3,4):
c2,4+с3,5>c2.5+c3.4 (30+40>30+100)
Количество единиц товара, перемещаемых по циклу: min (с2,4 ; с3,5)=15
В результате получится следующий план:
| B1 |
B2 |
B3 |
B4 |
B5 |
a |
| A1 |
45 |
60 |
40 |
60 |
95 |
90 |
| 15 |
30 |
45 |
| A2 |
35 |
30 |
55 |
30 |
40 |
50 |
| 15 |
20 |
15 |
| A3 |
50 |
40 |
35 |
30 |
100 |
30 |
| 30 |
| b |
15 |
45 |
45 |
50 |
15 |
170 |
Больше циклов с «отрицательной ценой» нет, значит, это оптимальное решение.
Проверим методом потенциалов:
Примем α1=0, тогда βj = cij – αi (для заполненных клеток).
Если решение верное, то во всех пустых клетках таблицы Δij = cij – (αi+ βj) ≥ 0
Очевидно, что Δij =0 для заполненных клеток.
В результате получим следующую таблицу:
| β1=45 |
β2=60 |
β3=40 |
β4=60 |
β5=70 |
| α1=0 |
45 |
60 |
40 |
60 |
95 |
90 |
| 15 |
30 |
45 |
0 |
+ |
| α2= -30 |
35 |
30 |
55 |
30 |
40 |
50 |
| + |
15 |
+ |
20 |
15 |
| α3= -30 |
50 |
40 |
35 |
30 |
100 |
30 |
| + |
+ |
+ |
30 |
+ |
| 15 |
45 |
45 |
50 |
15 |
170 |
Δ1,4=0 показывает, что существует еще один цикл с такой же ценой (1,2)-(1,4)-(2,4)-(2,2). Но так как при этом общая стоимость не изменится, то нет смысла менять перевозки.
Таким образом, решение верное, т.к. Δij ≥0.
ОТВЕТ:
| B1 |
B2 |
B3 |
B4 |
B5 |
a |
| A1 |
45 |
60 |
40 |
60 |
95 |
90 |
| 15 |
30 |
45 |
| A2 |
35 |
30 |
55 |
30 |
40 |
50 |
| 15 |
20 |
15 |
| A3 |
50 |
40 |
35 |
30 |
100 |
30 |
| 30 |
| b |
15 |
45 |
45 |
50 |
15 |
170 |
Задача 4
№59
Условие:
Определить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2 .
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежесткости.
| № |
b1 |
b2 |
c11 |
c12 |
c22 |
extr |
a11 |
a12 |
a21 |
a22 |
p1 |
p2 |
Знаки огр.
1 2
|
| 59 |
4.5 |
1.5 |
–5 |
–2 |
–1 |
max |
2 |
–3 |
5 |
4 |
9 |
13 |
³ |
³ |
Решение:
Целевая функция: F=-5x12-x22-2x1x2+4.5x1+1.5x2
Ограничения g1(x) и g2(x): 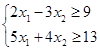 → →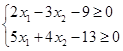
1) определим относительный максимум функции, для этого определим стационарную точку (х10, х20):
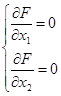 → → 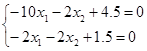 → → 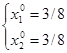
2) Исследуем стационарную точку на максимум, для чего определяем выпуклость или вогнутость функции
F11 (х10, х20) = -10 < 0
F12 (х10, х20) = -2
F21 (х10, х20) = -2
F22 (х10, х20) = -2
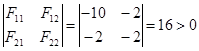
Т.к. условие выполняется, то целевая функция является строго вогнутой в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F(x)+u1g1(x)+u2g2(x)=
=-5x12-x22-2x1x2+4.5x1+1.5x2+u1(2x1-3x2-9)+u2(5x1+4x2-13)
Получим уравнения седловой точки, применяя теорему Куна-Таккера:
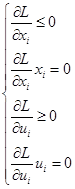 i=1;2 i=1;2
Объединим неравенства в систему А, а равенства в систему В:
Система А:
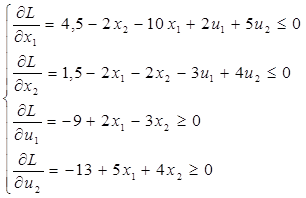
Система В:
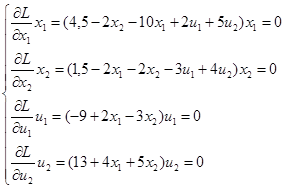
Перепишем систему А:
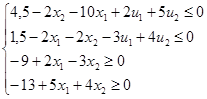
4)Введем новые переменные
V={v1,v2}≥0; W={w1,w2}≥0
в систему А для того, чтобы неравенства превратить в равенства:
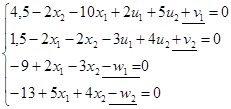
Тогда
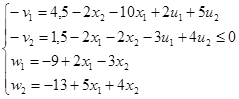 . .
Следовательно, система В примет вид:
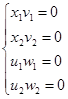 - это условия дополняющей нежесткости. - это условия дополняющей нежесткости.
5) Решим систему А с помощью метода искусственных переменных.
Введем переменные Y={y1; y2} в 1 и 2 уравнения системы
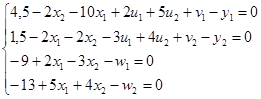
и создадим псевдоцелевую функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
В качестве свободных выберем х1, х2, v1, v2, u1, u2;
а в качестве базисных y1, y2, w1, w2.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
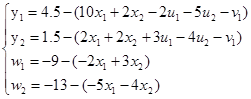
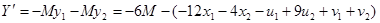
Решим с помощью симплекс-таблицы. Найдем опорное решение:
Примечание: вычисления производились программно, см Приложение
| b |
x1 |
x2 |
u1 |
u2 |
v1 |
v2 |
| Y' |
-6M |
-12M |
-4M |
-M |
9M |
M |
M |
| y1 |
4,5 |
10 |
2 |
-2 |
-5 |
-1 |
0 |
| y2 |
1,5 |
2 |
2 |
3 |
-4 |
0 |
-1 |
| w1 |
-9 |
-2 |
3 |
0 |
0 |
0 |
0 |
| w2 |
-13 |
-5 |
4 |
0 |
0 |
0 |
0 |
| b |
w1 |
x2 |
u1 |
u2 |
v1 |
v2 |
| Y' |
48M |
-6M |
-22M |
-1M |
9M |
1M |
1M |
| y1 |
-40,5 |
5 |
17 |
-2 |
-5 |
-1 |
0 |
| y2 |
-7,5 |
1 |
5 |
3 |
-4 |
0 |
-1 |
| x1 |
4,5 |
-0,5 |
-1,5 |
0 |
0 |
0 |
0 |
| w2 |
9,5 |
-2,5 |
-3,5 |
0 |
0 |
0 |
0 |
| b |
w1 |
x2 |
y1 |
u2 |
v1 |
v2 |
| Y' |
68,25M |
-8,5M |
-30,5M |
-0,5M |
11,5M |
1,5M |
1M |
| u1 |
20,25 |
-2,5 |
-8,5 |
-0,5 |
2,5 |
0,5 |
0 |
| y2 |
-68,25 |
8,5 |
30,5 |
1,5 |
-11,5 |
-1,5 |
-1 |
| x1 |
4,5 |
-0,5 |
-1,5 |
0 |
0 |
0 |
0 |
| w2 |
9,58 |
-2,5 |
-3,5 |
0 |
0 |
0 |
0 |
| b |
w1 |
x2 |
y1 |
y2 |
v1 |
v2 |
| Y' |
0 |
0 |
0 |
M |
M |
0 |
0 |
| u1 |
5,413043 |
| u2 |
5,934783 |
| x1 |
4,5 |
| w2 |
9,5 |
Т. о, w1=x2=y1=y2=v1=v2=0; u1=5,413043; u2=5,934783; x1=4.5; w2=9.5.
б) Условия дополняющей нежесткости не выполняются (u2w2≠0), значит решения исходной задачи квадратичного программирования не существует.
ОТВЕТ: не существует.
Приложение
#include <math.h>
#include <stdio.h>
main()
{
int i,j,k,m;
double h,n,a[5][7],b[5][7];
clrscr();
printf ("Введите числа матрицы А ");
for (i=0; i<5; i++){for(j=0; j<7; j++) {scanf ("%lf",&n); a[i][j]=n;}}
printf ("Введите координаты разрешающего элемента\n");
scanf("%d",&k) ;
scanf ("%d",&m);
printf (" матрицa A \n");
for (i=0; i<5; i++)
{for(j=0; j<7; j++) printf (" %lf",a[i][j]);printf ("\n");}
printf (" координаты \n ");
printf("%d %d",k,m) ;
h=1/a[k][m];
b[k][m]=h;
printf ("\n h=%lf",h);
for (i=0; i<7; i++)
{ if (i!=m) b[k][i]=a[k][i]*b[k][m]; }
for (i=0;i<5; i++)
{ if (i!=k) b[i][m]=-a[i][m]*b[k][m];}
for (i=0;i<5;i++)
{
for (j=0;j<7;j++)
if ((i!=k)&&(j!=m)) b[i][j]=a[i][j]+a[k][j]*b[i][m];
}
printf ("\n результат ");
printf (" матрицa B \n");
for (i=0; i<5; i++)
{for(j=0; j<7; j++) printf (" %lf",b[i][j]);printf ("\n");}
getch();
}
|