Министерство сельского хозяйства
Российской Федерации
Красноярский государственный аграрный университет
Кафедра менеджмента и
административного управления
Оптимизация производственной программы АПП
и управление запасами ресурсов
Расчетно-графическая работа по логистике
Выполнила:
студентка 4-го курса ИУиАБ Грицук Н.
Проверил:
профессор Ельдештейн Ю.М.
Красноярск 2010
Содержание
Введение……………………………………………………………3
1. Логистическая схема производственной системы агропромышленного предприятия………………………………………………………………4
2. Постановка задачи……………………………………………………..6
3. Аналитический метод решения задачи………………………………7
3.1. Решение задачи аналитическим методом
с использованием Excel………………………………………………….7
4. Графический метод решения задачи………………………………..10
4.1. Решение задачи графическим методом
с помощью Excel……………………………………………………..…10
5. Решение задачи……………………………………………………….13
5.1 Вторая итерация…………………………………………………….13
5.2 Третья итерация…………………………………………………….15
5.3 Четвертая итерация………………………………………………....17
5.4 Пятая итерация……………………………………………………...19
5.5 Шестая итерация……………………………………………………21
5.6 Седьмая итерация…………………………………………………...23
6. Решение задачи в условиях узкой специализации…………………25
6.1. Оптимизация запасов ресурсов при ограничении снизу (обязательное производство)……………………………………………………………27
6.2. Оптимизация запасов ресурсов при ограничении сверху (ограничения по реализации)…………………………………………………………...29
Заключение…………………………………………………………........31
Введение
Объектом изучения дисциплины «Логистика» являются материальные и связанные с ними информационные потоки. Логистика - наука об оптимизации материальных и информационных потоков с целью повышения управляемости производственных процессов и минимизации соответствующих финансовых затрат.
Основная задача агропромышленного комплекса - достижение устойчивого роста производства сельскохозяйственных продуктов, надежное обеспечение страны продуктами питания и сельскохозяйственным сырьем. Однако в условиях рыночных отношений, резкого обострения конкурентной борьбы одной из важнейших становится задача минимизации себестоимости продукции. Одной из основных составляющих себестоимости являются затраты на создание и хранение запасов ресурсов. Кроме того, отвлечение денег на создание и хранение неоправданно больших запасов одних ресурсов за счет других напрямую сказывается на величине обратных средств и объеме выпуска продукции, а, следовательно, на доходе .
1. Логистическая схема производственной системы
агропромышленного предприятия
Одним из основных звеньев в логистической цепи является Генеральное руководство. От генерального руководства ко всем остальным звеньям цепи направлены информационные потоки: поток документов, отчетов, запросов, принятие решений и т.д. Генеральное руководство осуществляет полное руководство и контроль на предприятии и следит за функционированием основных звеньев.
От генерального руководства к растениеводству, животноводству и птицеводству направлен поток информации в виде документов, в которых содержится информация о планах производства на месяц, на год и т.д., а также различные распоряжения, приказы и ряд другой документации. С основных производственных цехов к генеральному руководству направляются информационные данные о выполнении поставленных планов, о самом процессе производства, состояния производственного оборудования, о наличии или нехватке производственных мощностей и т.д.
Генеральное руководство делает запрос в университеты и предоставляет места для работы специалистам с высшим образованием (информационный поток). Специалисты из университетов направляются на работу либо в высшее руководство, либо размещаются по основным отделам (материальный поток). Это все происходит через отдел кадров. Из производственных цехов (животноводство и птицеводство) направляются информационные потоки в виде запросов на корма в растениеводство. Обратно же направляются материальные потоки в виде поставок комбикорма, силоса и других кормов.
Так как, любое предприятие является открытой системой, оно имеет входящие в систему закупаемые ресурсы и выходящую из системы конечную продукцию.
Логистическая схема структуры агропромышленного предприятия приведена на рисунке 1.
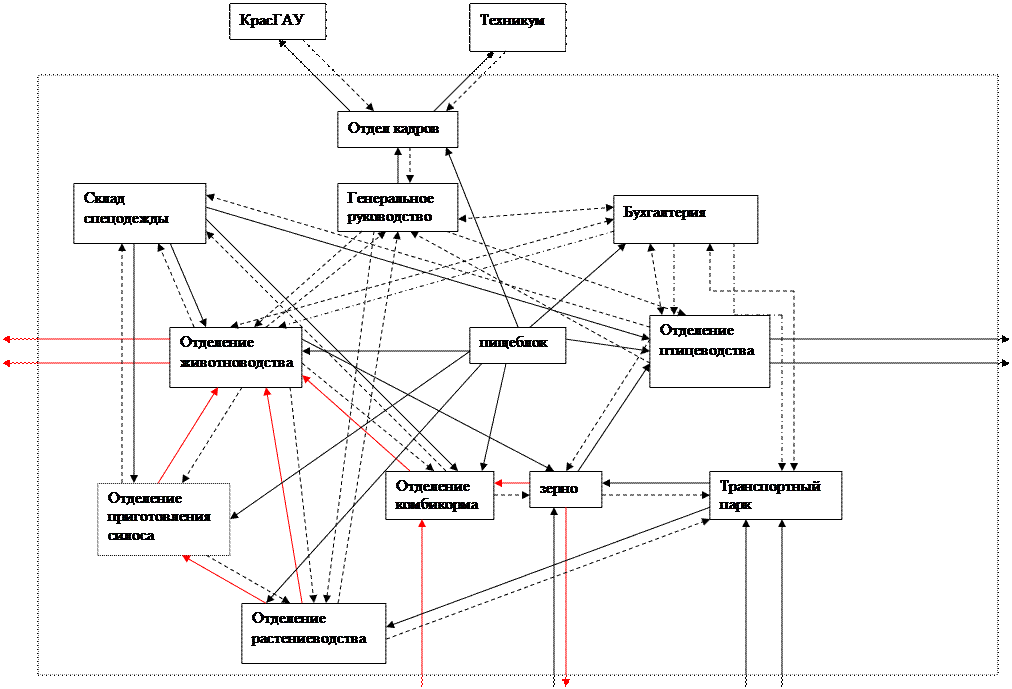
2. Постановка задачи
Агропромышленное предприятие (АПП) имеет возможность для производства крупного рогатого скота (КРС) и птицы. Для этого имеется соответствующие ресурсы, нормы которых и запасы приведены в таблице.
| Наименование ресурса |
Запас ресурса |
Цена ресурса за единицу, у.е. |
Нормы расхода ресурса |
| На 1 корову |
На десяток птиц |
| Силос, т |
1250 |
20 |
2,1 |
- |
| Комбикорм, т |
1000 |
100 |
1 |
0,54 |
| Зерно, т |
132 |
55 |
- |
0,6 |
| Выпас, га |
580 |
65 |
1 |
- |
| Трудовые ресурсы, чел |
5300 |
3,9 у.е. на 1 раб. В год |
10,5 чел/дн |
2,5 чел/дн |
Составим математическую модель задачи:
Пусть Х1 – количество КРС, которое можно произвести при данных запасах ресурсов,
Х2 – количество десятков индюков, которое можно произвести при данных запасах ресурсов.
2,1Х1 ≤ 1250;
Х1 + 0,54Х2 ≤ 1000;
0,6Х2 ≤ 132;
Х1 ≤ 580;
Х1 ≥ 0, Х2 ≥ 0;
F = 40Х1 + 10Х2 ®max.
3. Аналитический метод решения задачи
Аналитические методы абсолютно точны. Они дают возможность для точной количественной оценки излишков имеющихся ресурсов.
Приведем задачу к канонической форме:
2,1Х1 + Х3 = 1250;
Х1 + 0,54Х2 + Х4 = 1000;
0,6Х2 + Х5 = 132;
Х1 + Х6 = 580.
Дополнительные переменные Х3, Х4и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае - излишний запас).
3.1. Решение задачи аналитическим методом
с использованием Excel
Пусть имеется математическая модель:
2,1Х1 ≤ 1250;
Х1 + 0,54Х2 ≤ 1000;
0,6Х2 ≤ 132;
Х1 ≤ 580;
Х1 ≥ 0, Х2 ≥ 0;
F = 40Х1 + 10Х2 ®max
Для решения данной задачи необходимо в ячейки С10-
D
13
записать коэффициенты математической модели, в G
10-
G
14
правые части ограничений, а в C
3
и D
3
– коэффициенты целевой функции (рис. 1).
| КРС
|
Птица
|
Прибыль
|
max
|
| Значение
|
505 |
0 |
20190,47619 |
| Коэффициенты ЦФ
|
40 |
10 |
| Ограничения
|
| Расход
|
Запас
|
| Вид ресурса
|
Левая часть
|
Правая часть
|
Остаток
|
Остаток,%
|
| Силос
|
2,1 |
0 |
1060 |
<= |
1250 |
190 |
15,2 |
| комбикорм
|
1 |
0,54 |
504,7619048 |
<= |
1000 |
495,238 |
49,5 |
| Трудовые
|
10,5 |
2,5 |
5300 |
<= |
5300 |
0 |
0,0 |
| Зерно
|
0 |
0,6 |
0 |
<= |
132 |
132 |
100,0 |
| Выпас
|
1 |
0 |
504,7619048 |
<= |
580 |
75,2381 |
13,0 |
Рисунок 1. Пример формирования исходных данных
Далее следует щелкнуть мышкой на Сервис
, а затем Поиск решения
. На экране монитора появляется окно, изображенное на рисунке 2.
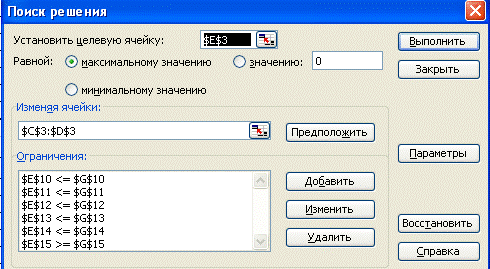
Рисунок 2. Пример экрана Поиск решения
После нажатия на Выполнить
появляется окно, изображенное на рис. 3, где можно посмотреть результаты и исследовать на устойчивость и пределы.
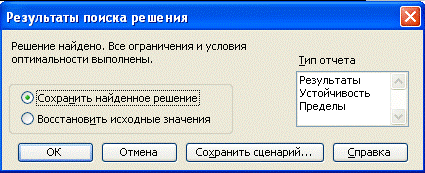
Рисунок3. Результаты поиска решения
После ОК
на экране появляются результаты решения, пример которых приведен на рис. 4.
| КРС
|
Птица
|
Прибыль
|
max
|
| Значение
|
505 |
0 |
20190,47619 |
| Коэффициенты ЦФ
|
40 |
10 |
| Ограничения
|
| Расход
|
Запас
|
| Вид ресурса
|
Левая часть
|
Правая часть
|
Остаток
|
Остаток,%
|
| Силос
|
2,1 |
0 |
1060 |
<= |
1250 |
190 |
15,2 |
| комбикорм
|
1 |
0,54 |
504,7619048 |
<= |
1000 |
495,238 |
49,5 |
| Трудовые
|
10,5 |
2,5 |
5300 |
<= |
5300 |
0 |
0,0 |
| Зерно
|
0 |
0,6 |
0 |
<= |
132 |
132 |
100,0 |
| Выпас
|
1 |
0 |
504,7619048 |
<= |
580 |
75,2381 |
13,0 |
Рисунок 4. Пример окончательного решения
Результаты расчетов Х1
и Х2
находятся в ячейках С3
и D
3
. Целевая функция - в ячейке E
3
. Столбец «Левая часть
» характеризует фактическое использование ресурсов. «Остаток
» определяется разностью между имеющимися запасами (Правая часть
) и их фактическим использованием (Левая часть
).
После завершения каждой итерации расчета результаты целесообразно сохранять под новым именем.
Для выполнения каждой последующей итерации достаточно лишь в столбце F
изменить числа, характеризующие запасы ресурсов.
Каждая итерация должна завершаться финансовой проверкой, которая состоит в том, что деньги, вложенные в ресурсы, должны оставаться неизменными. Кроме того, необходимо следить за тем, чтобы целевая функция после каждой итерации увеличивалась. Если это не происходит, значит, закуплен не дефицитный ресурс или избыточный ресурс продан в слишком большом количестве и стал дефицитным.
4. Графический метод решения задачи
Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Для каждого аналитического метода решения задачи существует соответствующий ему графический метод.
4.1. Решение задачи графическим методом
с помощью Excel
Программа MicrosoftExcel -2000 предназначена для работы с электронными таблицами, позволяющими собирать, анализировать и представлять количественную информацию в автоматическом режиме. Файл, создаваемый в Excel, называется рабочей книгой.
Для изображения линий, характеризующих ограничения, координаты соответствующих точек следует записать так, как это показано на рис. 5.
В ячейках M
7 –
M
11
– правые части ограничений – запасы ресурсов. В столбце В
задаются значения Х1
. Координаты Х2
вычисляются по уравнениям, характеризующим ограничения.
| Ресурс |
Х2 |
| Х1 |
Силос |
Комбик |
Зерно |
Выпас |
Труд.рес. |
F |
gradF |
| Силос |
595,2381 |
0 |
| 595,2381 |
2900 |
| Комбикорм |
0 |
1851,852 |
| 800 |
370,3704 |
| Зерно |
0 |
220 |
| 700 |
220 |
| Выпас |
580 |
0 |
| 580 |
2900 |
| Труд.рес. |
0 |
2120 |
| 700 |
-820 |
| F |
0 |
0 |
| -25 |
200 |
| gradF |
0 |
0 |
| 200 |
25 |
Рисунок 5. Пример записи исходных данных
Так как в ячейках M
7 –
M
11
находятся значения, характеризующие запасы ресурсов, то при каждом изменении запасов ресурсов, мы вводим в эти ячейки обновленные данные и получаем решение графическим методом.
Рисунок 6. Пример окончательного решения графическим методом
5. Решение задачи
5.1 Вторая итерация


5.2 Третья итерация


Четвертая итерация


Пятая итерация


Шестая итерация


Седьмая итерация


6. Решение задачи в условиях
узкой специализации
Узкая специализация позволяет улучшить качество и увеличить производительность за счет более простой типовой схемы движения предметов труда.
Определим рентабельность производства крупного рогатого скота и птицы как частное от деления прибыли на затраты на производство единицы продукции. Так как целесообразно производить более рентабельный продукт.

В данной задаче рентабельность производства крупного рогатого скота составляет:
RКРС
=(40/(2,1*20+1*100+1*65+10,5*3,9)*100=16%.
Рентабельность производства птицы составляет:
Rп=(10/(0,54*100+0,6*55+2,5*3,9)*100=5,4%.
Таким образом, в данном случае принимаем решение о производстве только крупного рогатого скота.
Имеющиеся денежные средства, вложенные в ресурсы, составляют 190630 у.е.
Эти деньги целесообразно вложить только в выращивание коров.
Определяем количество коров:
X1=190630/(2,1*20+1*100+1*65+10,5*3,9)=768,82
Тогда запасы ресурсов могут быть найдены из исходной модели при Х2=0:
Силоса 2,1*769=1614,9 т.;
Комбикорма 1*769=769 т.;
Выпаса 1*769=769т.;
Затраты трудовых ресурсов 10,5*769=8074,5
Далее переименовываем АнМет в Узкую специализацию (УС) и вводим подсчитанные данные в запасы.
Далее следует щелкнуть мышкой на Сервис
, а затем Поиск решения
. Затем нажимаем Выполнить
.
При этом будет получена прибыль в размере F=40*769=30760 у.е.
В таком случае математическая модель будет иметь вид:
2,1Х1 ≤ 769
Х1 + 0,54Х2 ≤ 769
0,6Х2 ≤ 0
Х1 ≤ 769
Х1≥0, Х2≥0
F = 40Х1 + 10Х2 ®max
Аналитическое решение этой задачи приведено на рис. 7, графическое решение на рис. 8

Рисунок 7. Аналитическое решение задачи в условиях узкой специализации производства

Рисунок 8. Графическое решение задачи в условиях узкой
специализации производства
Оценка экономической эффективности решения задачи оптимизации запасов при узкой специализации производства
Экономическая эффективность составляет:
Е= (30760-28191)/28191*100=9,1%
Таким образом, экономическая эффективность узкой специализации составила 9,1% или 2799 у.е.
6.1. Оптимизация запасов ресурсов при ограничении снизу
(обязательное производство)
Принимаем решение, что для собственного потребления нужно произвести 1500 птиц, т.е. 150 десятков.
Для этого необходимы ресурсы:
Силоса 0
Комбикорма 0,54*150=81 т.
Выпаса 0
Затраты трудовых ресурсов 2,5*150=375т.
Зерно 0,6*150=90т.
Для этого необходимы средства:
Д = 0 + 81*100 + 375*3,9 + 90*55 + 0 = 14512,5
Тогда на производство КРС остается: 190630-14512,5=176117,5
При этом количество КРС будет равно:
Х1 = 176117,5/(2,1*20+1*100+1*65+10,5*3,9) = 710,3
Тогда запасы ресурсов равны:
Силос 710,3*2,1=1491,63 т
Комбикорм 710,3*1 + 150*0,54 = 791,3 т
Зерно 150*0,6 = 90 т
Выпас 710,3*1=710,3 га
Трудовые ресурсы 710,3*10,5 + 150*2,5 = 7833,15 чел*дн
Аналитическое решение этой задачи приведено на рисунке 9, графическое решение на рис. 10.

Рисунок 9. Аналитическое решение при ограничении снизу

Рисунок 10. Графическое решение при ограничении снизу
6.2. Оптимизация запасов ресурсов при ограничении сверху
(ограничения по реализации)
Анализ рынка показал, что можно реализовать КРС в количестве не более 400 голов.
Для этого понадобятся ресурсы :
Силос 400 * 2,1 = 840 т.
Комбикорм 400 * 1 = 400 т.
Зерно 0 т.
Выпас 400 * 1 = 400 га
Трудовые ресурсы 400 * 10,5 = 4200 чел*дн
Определим деньги, необходимые для производства данного количества КРС:
Д = 400 * (2,1*20 + 1*100 + 65*1 + 10,5*3,9) = 99180
На производство остается: 74873
Х=74873 / (0,54*100+0,6*55+2,5*3,9) =302 птицы
Аналитическое решение этой задачи приведено на рисунке 11, графическое решение на рис. 12.

Рисунок 11. Аналитическое решение при ограничении сверху

Рисунок 12. Графическое решение при ограничении сверху
Заключение
Рассматриваемое агропромышленное предприятие имеет логистическую систему, состоящую из – генерального руководства, подразделения по производству продукции растениеводства, подразделения по производству продукции животноводства и птицеводства, цехов переработки: мясокомбинат, мелькомбинат, молокозавод.
При решении задачи линейного программирования традиционным итерационным методом удалось добиться почти полного использования запасов ресурсов. Их остатки составили менее одного процента от запасов. В этом случае может быть произведено 600 голов КРС и 343 десятков индюков. При этом может быть получено 25713 у.е. прибыли.
Узкая специализация работы весьма эффективна, т.к. позволяет организовать типовую схему движения предметов труда, резко сократить количество технологических маршрутов, повысить производительность. Было выявлено, что производство КРС наиболее рентабельно, чем производство птицы.
Затем задача была решена при дополнительных ограничениях «снизу» (обязательное производство птицы для собственного потребления) и «сверху» (ограничение по возможностям реализации КРС).
|