Теоретические зависимости для расчета сил, действующих на волокна в ремешковом вытяжном приборе кольцепрядильной машины, основаны на классификации зон вытяжного прибор этого типа. Выделим в нем следующие зоны (Рис. 1): 1,6 – зажимы соответственно выпускной и питающей пар; 2 – неконтролируемое пространство; 3 – ремешковый зажим; 4,5 – зоны между ремешковым зажимом и питающей парой, причем в зоне 4 располагается задний участок волокна. Эти зоны различны по геометрическим свойствам, свойствам поверхностей и скоростям, воздействующим на волокна мычки рабочих органов; в зонах 2 и 4 рабочие органы на мычку непосредственно не воздействуют (влияние ограничителя ширины мычки в данном исследовании пренебрегали).

Рисунок 1. Зоны ремешкового вытяжного прибора кольцепрядильной машины
Как наиболее общий случай рассмотрим силы, действующие на самое длинное волокно, располагающееся в зонах 1–4.
В зонах 1 и 3 в сечениях мычки можно выделить центральную область, все волокна которой контактируют только с соседними волокнами, и периферийную, волокна которой контактируют как с соседними волокнами, так и с поверхностями рабочих органов. В зонах 2 и 4 волокна периферийной области контактируют только с рядом расположенными волокнами, но число этих контактов меньше, чем в центральной области, так как область возможного контактирования их ограничена поверхностью мычки.
В любом сечении мычки контакты «волокно – волокно» могут вызывать появление как ускоряющих, так и сдерживающих сил, причем любое из этих событий имеет случайный характер. Скорости рабочих органов фиксированы, поэтому для быстро движущихся волокон контактирования с ремешками порождает сдерживающие силы, а для медленно движущихся и контактирующих с цилиндром или валиком – ускоряющие.
Закономерности сжатия мычки в вытяжном приборе определяются внешними сжимающими силами, действующими на рабочие органы, геометрическими и физическими свойствами поверхностей рабочих органов, а также свойствами волокон и мычки в целом. Эти силы сжимают мычку неравномерно как в продольном (ось У), так и в поперечном (ось Х) направлении. Это обуславливает различие в напряжение сжатия и в числе контактов, приходящихся на единицу длины одного волокна, что зависит от координат, которые характеризуют положение рассматриваемого участка волокна в поле вытягивания.
Обозначив символом mkj
(x, y) среднее число контактов волокна на единицу его дины, где j – условный номер зоны, k – тип контрпары, имеем классификацию фрикционных контактов волокон мычки по этим признакам (табл. 1)
Таблица 1. Классификация фрикционных контактов волокон мычки
| Тип контрпары k |
Зоны вытяжного прибора j |
| 1 |
2 |
3 |
4 |
| «Волокно-волокно» (в центральной области) |
m11
(x, y)
(c, y)
|
m21
(x, y)
(c, y)
|
m31
(x, y)
(c, y)
|
m41
(x, y)
(c, y)
|
«Волокно-волокно» (в периферийной области):
с валиком
с цилиндром
|
m12
(x, y)
(c, y)
m12
(x, y)
(c, y)
|
m22
(x, y)
(c, y)
|
m32
(x, y)
(c, y)
|
m42
(x, y)
(c, y)
|
| «Волокно-валик» |
m13
(x, y)
(y)
|
| «Волокно-цилиндр» |
m14
(x, y)
(y)
|
| «Волокно-ремешок» |
m35
(x, y)
(c)
|
В соответствии с этой классификацией в вытяжном приборе рассматриваемого типа имеются 12 типов контактов, в которых возникают соответствующие силы трения.
С учетом принятых на рис. 1 обозначений формула для сил трения, приходящихся на единицу длины волокна, примет вид
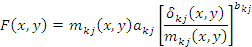
где 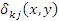 – напряжение поперечного сжатия волокон – напряжение поперечного сжатия волокон
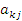 , , 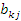 – эмпирические коэффициенты. – эмпирические коэффициенты.
Для ориентированного вдоль оси y волокна, ось конфигурации которого расположена на расстоянии x от продольной (вдоль оси y) плоскости симметрии мычки, имеем силы трения для зоны j:
Для волокон, расположенных в центральной области сечения мычки:
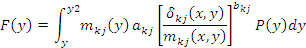
Для волокон, расположенных в периферийной области:

где y1
, y2
– границы участков волокна в соответствующих зонах вытяжного прибора, а остальные обозначения соответствуют аналогичным обозначениям в формуле (1).
Правая часть формулы (3) содержит два слагаемых. Первое, из которых соответствует силам трения в контактах «волокно – волокно», а второе – в контактах «волокно – рабочий орган». Формулы (2) и (3) могут использоваться для расчета как ускоряющих, так и сдерживающих сил в любой зоне вытяжного прибора. При этом, например, в случае ускоряющих сил коэффициенты akj
, bkj
, a,
kj
, b,
kj
, a,
kj
, b,
kj
. Соответствуют динамическому трению, а P(y) – вероятности контактирования с быстро движущимися волокнами. В альтернативном случае эмпирические коэффициенты соответствуют статическому трению, а P (y) – вероятности контактирования медленно движущимися волокнами.
На усредненное (гипотетическое) волокно в зонеj действует сила трения
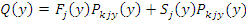 Где Где 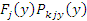 , , 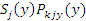 – вероятности принадлежности волокна с границами y1
и y2
к центральной и периферийной областям сечения мычки. – вероятности принадлежности волокна с границами y1
и y2
к центральной и периферийной областям сечения мычки.
На волокно некоторой протяженности ƛ, расположенного в зонах 1–4, действует сила
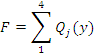
В зависимости от того, вычисляются ли по формулам (2) и (3) сдерживающие или ускоряющие силы отдельных зон, Fƛ
является соответствующей силой для всего волокна.
Вероятностные характеристики процесса рассчитываются по методике, изложенной в п. 3.3.2.4.
Среднее значение ускоряющей силы для волокна с длиной ƛ, оси конфигураций которых расположены на различных расстояниях х от плоскости симметрии мычки, равно
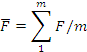
Где m – число волокон, использованных для расчета отдельных варьирующих значений F.
Аналогичным образом могут быть рассчитаны ускоряющие и сдерживающие силы, действующие на волокна различной длины, что дает возможность прогнозировать функцию движения волокон в вытяжном приборе прядильной машины в зависимости от параметров конструкции, режима работы и характеристик свойств волoкон и продукта и изменять её таким образом, чтобы отличие её от оптимальной функции было сведено к минимуму.
Силовой анализ вытяжного прибора с круглым гребнем
Поле вытягивания прибора с круглым гребнем состоит из зон (Рис. 2), каждой из которых присущи индивидуальные закономерности, характеризующие силы, действующее на волокна мычки: 1–2 – зона эластичного зажима мычки в выпускной паре; 2–3 – зона огибания валика мычкой; 3–4 – зона вредного пространства; 4–5 – Зона взаимодействия с иглами круглого гребня; 5–6 – зона взаимодействия с иглами и основанием круглого гребня; зоны 6–7 и 7–8 аналогичны соответственно зонам 4–5 и 3–4. Зона 8–9 питающей пары далее не рассматривается, так как разводка в вытяжном приборе существенно превышает максимальную длину волокна в утоняемой ровнице.
Формирование силового поля вытяжного прибора данного типа осуществляется как результат: взаимодействия волокон мычки и волокон мычки с поверхностями рабочих органов на линейных и близких к линейным зонах или участках зон (способ 1); взаимодействие волокон мычки между собой и с поверхностями цилиндрических рабочих органов (способ 2); взаимодействие волокон мычки с поверхностями игл и между собой в межигольном пространстве (способ 3).
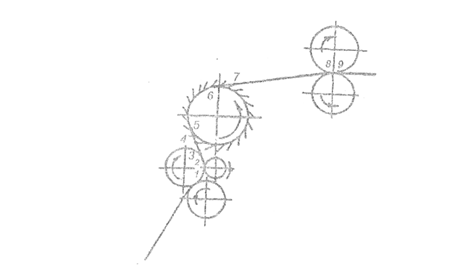
Рисунок 2. Зоны вытяжного прибора с круглым гребнем
В таблице 2 приведены способы формирования силового поля для соответствующих зон вытяжного прибора.
Анализ показывает, что в зонах 4, 5, 6 силовые поля созданы комбинациями способов; зона 1 имеет небольшую протяженность и малую кривизну, что с некоторой погрешностью позволяет отнести способ формирования в ней силового поля к способу 1.
Табл. 2 Способы формирования силовых полей различных зон вытяжного прибора
| Условный номер зоны j |
Способ формирования силового поля |
| 1 |
2 |
3 |
| 1 |
+ |
| 2 |
+ |
| 3 |
+ |
| 4 |
+ |
+ |
| 5 |
+ |
+ |
| 6 |
+ |
+ |
| 7 |
+ |
Зона обозначена по условному номеру ее границы, ближайшей к зажиму выпускной пары А (Рис. 2).
Определим действующие на волокна силы в вытяжном приборе с учетом способов формирования силовых полей.
Способ 1.
В j-й зоне (зоны 1, 3, 4, 5, 7) волокно может располагаться в центральной (с) или периферийной (р) областях сечений мычки с вероятностями соответственно Рjc
(y) и Pjp
(y), при этом действующие на волокна в этих областях силы различны по величине, а волокна могут двигаться либо со скоростью выпускной пары, либо со скоростью круглого гребня. В первом случае трение является динамическим (d) и вызывает силы, ускоряющие (u) волокна, во втором – статическим (s) и предопределяет тормозящие (t) силы.
Если общим символом F
обозначит силы, а символом y – координату силового поля, то с учетом приведенной выше символики для ускоряющих сил, действующих на волокно внутри мычки (взаимодействие между волокнами w), будем иметь
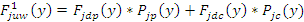
В зоне 1 волокна контактируют с вероятностью Рlz
(y) c цилиндром и Рlv
(y) – с валиком; при этом действующие ускоряющие силы соответственно Fldz
(y) и Fldv
(y).
Ускоряющая сила в зажиме выпускной пары:
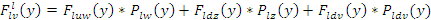
где 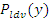 ) – вероятность контактирования в зажиме между волокнами. ) – вероятность контактирования в зажиме между волокнами.
Для определения величин сил Fjdp
(y) и Fjdz
(y), Fldv
(y), входящих в формулы (7) и (8) используется формула Линкольна. Она имеет общую структуру для различных сил, но входящие в неё параметры различны по величине и зависят от природы контртела, с которым взаимодействует рассматриваемое волокно. Так например, динамическая сила трения волокна о волокно в периферийной области сечения мычки будет
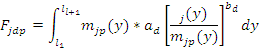
Lj
, Lj
1
l
– координаты границы j зоны;
Mjp
(y) – число контактов на единицу длины волокна в периферийной области сечения мычки j-й зоны;
Аd
, Bd
– эмпирические коэффициенты, соответствующие динамическому трению волокна о волокно.
Формулы (7) и (9) могут быть использованы для расчета тормозящих волокно сил любой из зон (Табл. 2) с соответствующей заменой индексов u
на t
, d
на s
, а в соответствующих случаях p
на с
. Так, для тормозящей силы имеем
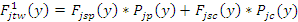
Способ 2.
В j-й зоне волокно может контактировать с волокнами (w), которые движутся со скоростью выпускной пары, вызывая динамическое трение (d) и ускоряющие силы (u) – c вероятностью этого события Pjwd
(y) или со скоростью круглого гребня, вызывая статическое трение (s) и соответственно тормозящие силы (t) – с вероятностью такого события Pjws
(y). Кроме того, волокно мычки может контактировать с валиком (j=2) что вызывает ускоряющую силу (u) или с основания гребня, что вызывает тормозящую силу (t) с соответствующими вероятностями P2
v
(y) и P5
d
(y).
Ускоряющая сила, например, для j=2 будет
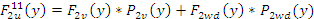 , а тормозящая сила для этой зоны , а тормозящая сила для этой зоны 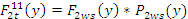 для зоны 5 значение тормозящей силы может быть найдено по формуле для зоны 5 значение тормозящей силы может быть найдено по формуле
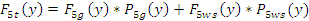
где g – символ взаимодействия волокон с основанием круглого гребня, а ускоряющая сила будет
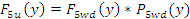
Значение величин сил, входящих в формулы, могут определяться по формуле, аналогично приведенной в работе (91). Например, определение силы P2
v
(y) на любой части угла α от охвата валика мычкой можно осуществить по формуле
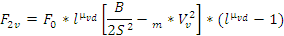
где 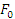 -сила динамического трения в точке, соответствующей началу ведомого участка дуги, стягивающий угол ɓ; -сила динамического трения в точке, соответствующей началу ведомого участка дуги, стягивающий угол ɓ;
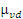 – динамический коэффициент трения волокна о валик; – динамический коэффициент трения волокна о валик;
В - изгибная жесткость волокна;
S = R+d/2,
где R – радиус валика; в – диаметр волокна;  -масса единицы длины волокна; -масса единицы длины волокна; 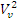 -скорость выпускной пары вытяжного прибора. -скорость выпускной пары вытяжного прибора.
Выражение (15) может быть использовано: для определения натяжения волокна на любом участке зоны 2; этот принцип применим и для зоны 5; для определения тормозящих (j=2) или ускоряющих (j=5) сил в результате огибания рабочих органов соответственно быстро движущимися и медленно движущимися волокнами, которые находятся внутри мычки, для чего формула (15) подлежит преобразованию с заменой необходимых случаях индексов v на g, в на s, Vv
на Vg
(скорость круглого гребня).
Способ 3.
В j-й зоне (зоны 4, 5, 6) волокно может контактировать с вероятностью Pjwd
(y) c волокнами (w), которые движутся со скоростью выпускной пары, вызывая динамическое трение (d) и ускоряющие силы (u), или контактировать с вероятностью Pjws
(y) с круглым гребнем, при этом возникают статическое трение (s) и соответственно тормозящие силы (t). Кроме того, волокно может контактировать с иглами с вероятностью Pji
(y), а в зоне 5 и с основанием гребня с вероятностью P5ij
(y).
С учетом принятых ранее обозначений ускоряющая сила
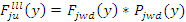
а тормозящая
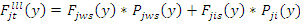
где индекс i – характеризует взаимодействие волокна и иглой.
При взаимодействии волокна с иглой необходимо учесть силы, которые прижимают волокно к поверхности иглы. Эти силы обусловлены сжатием мычки в межигольном пространстве круглого гребня.
Значение силы 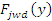 , , 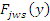 , , 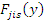 определяется по общей (по структуре) формуле, но с соответствующими изменениями входящих в формулу величин. определяется по общей (по структуре) формуле, но с соответствующими изменениями входящих в формулу величин.
Кроме того, для каждой иглы и последующего межигольного пространства последовательно применяются однотипные формулы с учетом способов формирования силовых полей в соответствующих зонах.
Для определения, например, силы 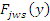 , на дуге охвата φ иглы применима формула , на дуге охвата φ иглы применима формула
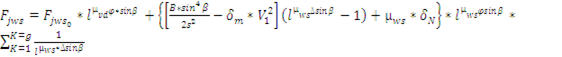 , ,
где 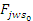 -сила статического трения в точке, соответствующей началу ведомого участка дуги, стягивающей углы ∆, на которые разбивается угол охвата иглы волокном φ (число углов ∆ равно g). -сила статического трения в точке, соответствующей началу ведомого участка дуги, стягивающей углы ∆, на которые разбивается угол охвата иглы волокном φ (число углов ∆ равно g).
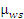 – статический коэффициент трения волокна о волокно мычки в межигольном пространстве; – статический коэффициент трения волокна о волокно мычки в межигольном пространстве;
β – угол наклона расположения мычки к оси иглы. Остальные обозначения в формуле (15) с учетом изменения индексов v на w, в на s, Vv
наVt
.
Область применения формулы (18) характеризуется теми же условиями, которые были указаны выше для формулы (15)
Наиболее сложной для определения сил, действующих на волокно, является зона 5, где необходимо в зоне действия игл гребня применять зависимости, характеризующие способы 1 и 3 формирования полей сил, учитывая вероятностный характер взаимодействия волокна как с волокнами (быстро или медленно движущимися) так и с иглами и с основанием круглого гребня.
Для волокна длиною L ускоряющая (сдерживающая) сила будет определяться суммой соответствующих сил в зонах, в пределах которых это волокно в данный момент расположено.
Полученные аналитические зависимости могут быть использованы для целенаправленного изменения конкретных характеристик свойств волокон, технологических и конструктивных параметров вытяжного прибора с целью управления силами, действующими на волокна, закономерностью их движения и снижения неровноты от вытягивания
В работе (81) получено следующее аналитическое выражение для определения толщины мычки в эластичном зажиме вытяжного прибора прядильной машины с круглым гребнем:
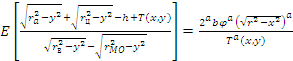 , ,
где r
– радиус поперечного сечения ровницы до её утонения;
x
,
y
– координаты точки напряжения сжатия по известной толщине мычки изложен ранее в пункте 3. 3. 2. 1.
Расчеты осуществлялись по программе MatLAB, при этом толщина мычки t (x, y) и напряжение сжатия мычки δ (x, y) определялись при разных величинах модуля на сжатие эластичного покрытия. Численное моделирование осуществлялось применительно к вытяжному прибору с круглым гребнем (rц
= 9,5 мм, rв
= 16 мм, h = 24,8 мм, φ = 0,045 мг/мм3
, rмо
= 12 мм, b = 72328, r = 1 мм). Этим условиям соответствует получение пряжи линейной плотности 180 Текс (шерсть 100%) при вытяжке 1,6. На рис. 3 представлено изменение толщины мычки в зажиме при E = 40*102
мН/мм2
при различных значениях х
и удаления плоскостей от диаметральной плоскости валика и цилиндра на 0, 0,8, 1,2, 1,6, 2,0 мм (соответственно кривые 1, 2, 3, 4, 5).

Рисунок 3. Толщина мычки в различных сечениях эластичного зажима вытяжного прибора с круглым гребнем
Эти данные показывают, что в диаметральной плоскости валика и цилиндра продукт сжат в наибольшей степени; по мере удаления от нее толщина мычки увеличивается, а степень сжатия уменьшается.
Мычка имеет наибольшую толщину вдоль плоскости, проходящей через продольную ось продукта, перпендикулярную к осям валика и цилиндра.
На рисунке 3 показаны изменения величины напряжений сжатия эластичного покрытия валика на всей протяженности его контакта с цилиндром и продуктом, при этом кривая 1 соответствует диаметральной плоскости валика и цилиндра (y = 0), а кривые 2….6 соответствуют плоскостям, отстоящим от диаметральной плоскости на 0,4…….. 2,0 мм.
Эти результаты свидетельствуют, что напряжение эластичного покрытия (оно же – напряжение сжатия продукта) в зажиме неравномерно и максимальное его значение соответствует минимальной толщине мычки, причем по мере удаления от диаметральной плоскости валика и цилиндра эти напряжения уменьшаются.
В таблице 3 приведены величины напряжений δп
(x, y) в мН/мм2
для двух значений модуля деформации сжатия эластичного покрытия E и различных значений координат x, y. Из анализа результатов, приведенных в таблице 3, следует, что при большей жесткости эластичного покрытия напряжение сжатия мычки характеризуется большей стабильностью вдоль оси x, что создает лучшие условия для процесса вытягивания. Полученные результаты в качественном отношении совпадают с результатом работы.
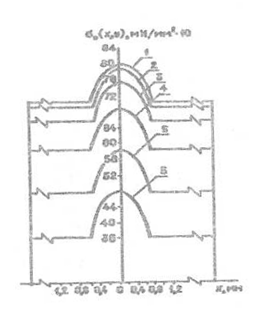
Рисунок 4. Изменение напряжения сжатия мычки в эластичном зажиме вытяжного прибора прядильной машины с круглым гребнем
Таблица 3. Напряжение сжатия мычки в эластичном зажиме при различных значениях модуля деформации сжатия эластичного покрытия, мН/мм2
| E, мН/мм2
|
x, мм |
y, мм |
| 0 |
0,4 |
0,8 |
1,2 |
1,6 |
2,0 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 20*102
|
0 |
409,5 |
404,5 |
385,5 |
353,1 |
306,2 |
252,8 |
| 0,2 |
408,5 |
403,5 |
380,1 |
351,6 |
304,7 |
249,9 |
| 0,4 |
404,5 |
399,5 |
372,6 |
347,6 |
300,3 |
346,4 |
| 0,6 |
397,5 |
393,0 |
380,6 |
340,2 |
292,3 |
237,5 |
| 0,8 |
385,5 |
380,5 |
350,6 |
327,2 |
378,4 |
222,2 |
| 1,0 |
350,0 |
345,0 |
324,2 |
289,3 |
238,2 |
177,8 |
| 100*102
|
0 |
1922,5 |
1897,5 |
1798,0 |
1630,9 |
1387,1 |
1106,2 |
| 0,2 |
1917,5 |
1895,0 |
1783,0 |
1625,9 |
1384,6 |
1101,2 |
| 0,4 |
1907,5 |
1887,5 |
1778,1 |
1616,0 |
1369,7 |
1088,9 |
| 0,6 |
1887,5 |
1862,5 |
1760,6 |
1593,5 |
1347,4 |
1061,4 |
| 0,8 |
1852,5 |
1827,5 |
1725,7 |
1556,1 |
1307,7 |
1017,3 |
| 1,0 |
1750,0 |
1725,0 |
1621,0 |
1446,4 |
1191,1 |
888,9 |
Напряжение нормального давления в ремешковом зажиме обуславливает закономерность движения волокон в вытяжном приборе и неровноту по толщине от вытягивания. В сечении мычки, расположенном на расстоянии y
от начала координат (Рис. 5), это напряжение определяется по формуле

где 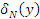 – давление верхнего ремешка 1 на нижний 2 (при отсутствии мычки между ремешками); – давление верхнего ремешка 1 на нижний 2 (при отсутствии мычки между ремешками);
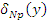 – давление на мычку от растяжения ремешка в поперечном направлении; – давление на мычку от растяжения ремешка в поперечном направлении;
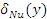 – давление верхнего ремешка на мычку от его изгиба. – давление верхнего ремешка на мычку от его изгиба.

Рисунок 5. Схема ремешкового зажима вытяжного прибора кольцепрядильной машины (1,2 – соответственно верхний, нижний ремешок, 3,4 – соответственно промежуточный валик, цилиндр вытяжного прибора, S – центр кривизны платформы нижнего ремешка)
Согласно работе (80)
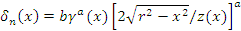
где a, b – эмпирические коэффициенты;
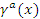 , r – соответственно объемная плотность сечения мычки и радиус продукта до сжатия; , r – соответственно объемная плотность сечения мычки и радиус продукта до сжатия;
z(x) – z-координата сечения мычки, равная прогибу верхнего ремешка;
 – степень сжатия мычки. – степень сжатия мычки.
Выделим из изогнутого верхнего ремешка 1 элемент s
с размерами, например, 1 мм при ширине ремешка c
и толщиной h
(Рис. 6)

Рисунок 6. Схема взаимного положения ремешков (1, 2), промежуточных валика (3) и цилиндра (4)
Отождествим изогнутый элемент s
ремешкас плоской пружиной (Рис. 4), прогиб которой z(x) в сечениях x, смещенных друг относительно друга на единицу длины, обусловлен напряжением
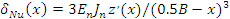
где B – ширина мычки; 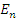 – модуль поперечного изгиба ремешка; – модуль поперечного изгиба ремешка; 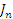 – момент инерции сечения. – момент инерции сечения.
Пусть на элементе s имеем участок ab с длиной до изгиба l (положение 1,
ремешка 1)
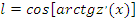
После растяжения (в зонах M и N смещение ремешков отсутствует) длина этого участка
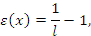
давление на мычку m от растяженного ремешка l
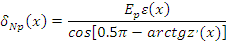
где 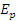 – Модуль растяжения верхнего ремешка в поперечном направлении. – Модуль растяжения верхнего ремешка в поперечном направлении.
Напряжение 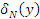 подчинено различным закономерностям на участках AB, BC, и CD в силу различных условий его формирования. подчинено различным закономерностям на участках AB, BC, и CD в силу различных условий его формирования.
На участке AB осуществляется фрикционная передача валика 3 и цилиндра 4 через расположенные между ними ремешки 2 и 1. На этом участке действует сила сжатия:
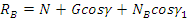
где N – нагрузка (от рычага нагрузки) на промежуточную пару 3,4;
γ – угол наклона вытяжного прибора;
γ1
– угол между направлениями действия сил N и NB
;
G – часть веса верхней клеточки, приходящаяся на эту опору;
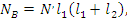
где 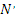 – сила упругости пружины j0
, деформированной в результате действия на нее в точке К рычага нагрузки. – сила упругости пружины j0
, деформированной в результате действия на нее в точке К рычага нагрузки.
На единицу длины участка Lc
– бортика промежуточного валика 3 (Рис. 6) приходится нагрузка
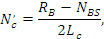
где 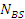 – сила сжатия, действующая на участке – сила сжатия, действующая на участке 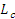 , причем ширина контактной площадки AB в области бортиков (94): , причем ширина контактной площадки AB в области бортиков (94):
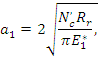
где 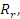 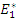 – соответственно приведенные радиус и модуль упругости контактируемых тел. – соответственно приведенные радиус и модуль упругости контактируемых тел.
Поскольку жесткость контртел на участке 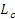 больше, чем на участке больше, чем на участке 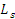 , следует равенство (Рис. 6) , следует равенство (Рис. 6)

Рисунок 7. Схема взаимного положения ремешков (1, 2), промежуточных валика (3) и цилиндра (4)
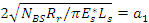
где 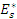 – приведенный модуль упругости ремешков 1 и 2. – приведенный модуль упругости ремешков 1 и 2.
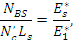
и, кроме того,
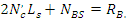
Решая совместно уравнения (31) и (32), определяем силу 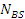 и, следовательно, её удельное значение: и, следовательно, её удельное значение:
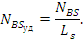
Распределение напряжений на участке АВ (Рис. 7) (94):
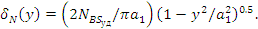
Напряжение 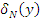 создает силу трения Fk
в зажиме промежуточной пары 3, 4 и уменьшает напряжение F2
ведущей ветви ремешка, что наблюдалось бы при отсутствии фрикционной системы (промежуточный валик 3 в этом случае выполняет роль ведущего шкива): создает силу трения Fk
в зажиме промежуточной пары 3, 4 и уменьшает напряжение F2
ведущей ветви ремешка, что наблюдалось бы при отсутствии фрикционной системы (промежуточный валик 3 в этом случае выполняет роль ведущего шкива):
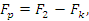
где 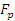 – натяжение ремешка на границе участка AB (в точке B). – натяжение ремешка на границе участка AB (в точке B).
Определяем F2
. Пусть F1
– напряжение ведомой ветви ремешка; T – сила, необходимая для скольжения ремешка 1 по контактной площадке пружины J; Fr
– сила давления на ось промежуточного валика, обусловленная натяжением ветвей ремешка. Тогда, в соответствии с работами (95) и (96)
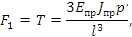
где 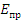 – модуль на изгиб плоской пружины J; – модуль на изгиб плоской пружины J;
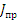 – момент инерции сечения; – момент инерции сечения;
l – длина пружины;
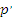 – радиус контактной площадки пружины. – радиус контактной площадки пружины.
Кроме того,
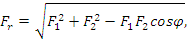
где φ – угол охвата валика.
Определим равнодействующую силу F, N, NB
и G путем последовательного сложения этих сил:
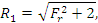
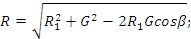

где углы α и β определимы геометрически.
Передаваемое усилие
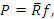
где f – приведенный к валу коэффициент трения.
Напряжение ремешка 1 в точке схода его с валика 2
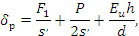
где 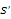 , ,  , , 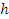 – соответственно площадь поперечного сечения, модуль продольного изгиба и толщина ремешка 1; – соответственно площадь поперечного сечения, модуль продольного изгиба и толщина ремешка 1;
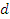 – диаметр промежуточного валика 3. – диаметр промежуточного валика 3.
Натяжение ремешка 1 в точке схода:
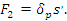
Совместное решение уравнений (37) и (43) позволяет определить F2
и согласно формуле (35) рассчитать Fp
.
На участке CD у точки в сила начального натяжения верхнего ремешка по Л. Эйлеру:
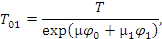
где  – коэффициент трения ремешка по стали (пружина J); – коэффициент трения ремешка по стали (пружина J);
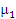 – коэффициент трения ремешка по направляющей Q; – коэффициент трения ремешка по направляющей Q;
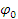 , , 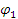 – соответствующие углы охвата. – соответствующие углы охвата.
Разобьем угол φ на малые углы ∆φ, каждый из которых опирается на дугу равную единице длины. На каждый участок i ремешка действует: сила T0
i
начального напряжения; сила Ti
натяжения ведущего конца участка; давление на единицу длины ремешка 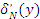 и сила трения контрпары «ремешок – ремешок» и сила трения контрпары «ремешок – ремешок» 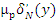 ( (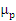 – коэффициент трения). – коэффициент трения).
Из условия равновесия единичного участка ремешка
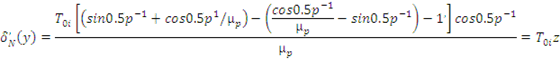
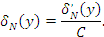
Последовательное применение уравнений (45) и (46) позволяет определить δN
(y) на всем протяжении участка CD; у точки С участка сохраняется натяжение верхнего ремешка:
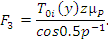
На участке BC можно предполагать близкую к линейной закономерность изменения силы трения, поэтому
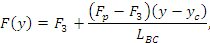
где 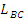 – длина участка BC; – длина участка BC;
 – координата точки С. – координата точки С.
Разобьем участок BC на малые участки длиной, равной единице, и, определив F(y) для концов каждого из них, найдем прирост силы трения ∆F(y); тогда для каждого участка
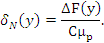
Расчет 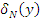 на ЭВМ выявил закономерность его изменения (Рис. 8). на ЭВМ выявил закономерность его изменения (Рис. 8).

Рисунок 8. Эпюра напряжения поперечного сжатия мычки в ремешковом зажиме кольцевой прядильной машины.
Полученные результаты показывают, что распределение имеет сложную форму и в качественном отношении соответствуют выводам, приведенным в работах (65) и (66).
|