Сборник задач и расчетно-графических работ по технологии переработки полимеров
Содержание
1. Формование изделий (1,2,3,4,5,6,7)
2. Характеристики волокнистых наполнителей (8,9,10)
3. Отверждение термореактивных связующих (11,12,13,14,15,16)
4. Физико-химическое взаимодействие между связующим и наполнителем в переходных слоях(17,18,19,20,21,22,23,24,25,26,27,28,29,30)
5. Диффузионные процессы в системе «связующее-наполнитель» (31,32,33,34,35,36,37,38,39,40,41,42,43)
6. Структура и свойства сетчатых полимеров (44,45)
7. Материальные расчеты (46,47)
8. Статистическая обработка результатов измерений (48)
1. Рассчитать массовую скорость m , г / мин истечения расплавленного поликапроамида при линейной скорости формования v=700 м/ мин капроновой нити метрического номера N=10,7 , если плотность капрона ρ=1,14 г/ см3
. Рассчитав эффективное сечение нити S,мкм2
по соотношению
S=106
/ Nρ , определите условный радиус нити r.
Решение:
Толщина нити в текстах Т=1000/N=93,4 г/1000м
S= ≈82000 мкм2
=8,2·10-4
см2
. ≈82000 мкм2
=8,2·10-4
см2
.
Объёмная скорость V истечения расплава V=v·
S=7·104
cм/мин·8,2·104
см2
=57,4 см3
/мин
Массовая скорость истечения расплава
m=V·ρ=57,4 cм3
/мин·1,14 г/см3
=65,4 г/мин=1,09·10-3
кг/с
S=πr2
; r=√S/π=√82000/3,14=160 мкм
Ответ:
m=65,4 г/мин; r=160 мкм
2. Пользуясь законом Пуазейля m= , определить поправку q, характеризующую отклонение реального полимера от ньютоновской жидкости. Принять : m=65,4 г/мин =1,09·10-3
кг/с. ∆P=10кгс/см2
=1,02·106
Па; r=160мкм; ρ=1,14 г/см3
; ℓ=1см ; η=8 Па·с , определить поправку q, характеризующую отклонение реального полимера от ньютоновской жидкости. Принять : m=65,4 г/мин =1,09·10-3
кг/с. ∆P=10кгс/см2
=1,02·106
Па; r=160мкм; ρ=1,14 г/см3
; ℓ=1см ; η=8 Па·с
Подсчитать, во сколько раз понизилась вязкость при течении? Какова причина этого явления?
Решение:
Для расчёта величины q из указанного соотношения все входящие в него величины необходимо выразить в единицах системы СИ:
∆P=10кгс/см2
=10/9,8 МПа=1,02 МПа=1,02·106
Па
r=160 мкм=160·10-6
м=1,6·10-4
м; ρ=1,14 г/см3
=1,14·10-3
кг/см3
=1140 кг/м3
; ℓ=1см=10-2
м;
q=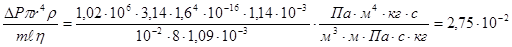 ; ;
В начальном состоянии : η1
=ηн
В конечном состоянии : η2
=ηк
=0,0275ηн
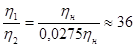
Ответ:
q=2,75·10-2
; вязкость полимера понизилась в 36 раз.
3. Найти показатель степени m в обобщённом законе течения жидкостей σ=η·γm
, если при увеличении напряжения σ в 2 раза скорость деформирования γ увеличилась в 12 раз, а вязкость η жидкого полимера понизилась в 5 раз. О каких структурных изменениях в полимере свидетельствует полученное значение m?
Решение
Записываем обобщённый закон течения в начальном и конечном состояниях рассматриваемой системы:
σ1
=η1
γ1
m
2σ1
=0,2η1
·12m
γ1
m
Почленно логарифмируем эти соотношения:
ℓgσ1
=ℓgη1
+mℓgγ1
ℓg2+ℓgσ1
=ℓg0,2+ℓgη1
+mℓg12+mℓgγ1
и вычитаем одно из другого:
ℓgσ1
-ℓg2-ℓgσ1
=ℓgη1
+mℓgγ1
-ℓg0,2-ℓgη1
-mℓg12-mℓgγ1
После взаимного уничтожения некоторых слагаемых получаем алгебраическое уравнение:
+ℓg2=+mℓg12+ℓg0,2;откуда m= ≈0,92 ≈0,92
Ответ:
m=0,92; значение m‹1 свидетельствует об уменьшении размера надмолекулярных структур в процессе переработки полимера.
4.Найти напряжение σ, при котором вязкость расплава поликапроамида составляет η=9 Па·с при скорости деформирования γ=0,3 мин-1
, если показатель степени в обобщённом законе течения σ=ηγm
m=0,92.
Решение:
γ=0,3 мин-1
= с-1
=0,005 с-1 с-1
=0,005 с-1
Применяем обобщённый закон течения:
σ=9·0,0050,92
;
ℓgσ=ℓg9+0,92ℓg(5·10-3
)=ℓg9+0,92ℓg5-2,760=0,954+0,92·0,699- 2,76=0,954+0,643-2,760=-1,163. Следовательно σ=10-1,163
≈0,07 Па
Ответ
: σ=0,07 Па
5. Вычислить среднюю массу 
 межузловых цепей в сетчатом полимере, если модуль упругости при растяжении Ер
=109
Па. Расчёт проводить по соотношению межузловых цепей в сетчатом полимере, если модуль упругости при растяжении Ер
=109
Па. Расчёт проводить по соотношению  где Т=393 К, ρ=1200 кг/м3
, R=8,31 Дж/моль·К. Каково соотношение между модулями упругости при растяжении и межслоевом сдвиге? где Т=393 К, ρ=1200 кг/м3
, R=8,31 Дж/моль·К. Каково соотношение между модулями упругости при растяжении и межслоевом сдвиге?
Решение
 = =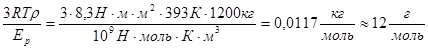
Полученное среднее значение массы межузловых цепей Мс
=12 г/моль соответствует физическим узлам ветвления (перепутывания), поскольку физические сетки значительно более частые, чем химические сетки.
Ответ
: Мс
=0,012 кг/моль=12 г/моль
6. Вычислить среднюю толщину в прослойки связующего при равномерном распределении однонаправленных элементарных волоконец в материале. В качестве наполнителя используется техническая нить капрон с линейной плотностью Т=90.Масса прессованного образца 40 г при массовом соотношении связующего и наполнителя 1:1. Плотность эпоксидного связующего ρсв.
=1,2 г/см3
, плотность капрона ρкапр
=1,14 г/см3
.Для расчёта применить соотношение
d = 
где mсв.
и mнап.
- масса связующего и наполнителя в образце, г, соответственно.
Указанное соотношение получено для модели равномерного распределения армирующих волоконец в поперечном сечении образца ПКМ. При этом суммарная площадь промежуточных слоёв определяется как разность общей площади поперечного сечения образца и суммарной площади поперечных сечений армирующих волоконец.
Решение


Ответ:
d≈0,07 мм=0,007 см=70 мкм
7. Определить объём V, см3
, децинормального (0,1 н) раствора соляной кислоты, пошедшего на нейтрализацию основных групп, содержащихся в 1 см3
смеси эпоксидная смола ЭД-20 -отвердитель полиэтиленполиамин (ПЭПА) по соотношению
V=N
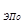 (1-xэп
)v
эп
+(N
(1-xэп
)v
эп
+(N
 -
-
 xэп
N
xэп
N
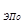 )v
отв
,
)v
отв
,
где v
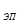 =1,4∙10-20
; v
отв
=3∙10-20
объём кислоты на нейтрализацию одной функциональной группы смолы и отвердителя, см3
;
=1,4∙10-20
; v
отв
=3∙10-20
объём кислоты на нейтрализацию одной функциональной группы смолы и отвердителя, см3
;
N
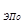 =3,6∙1020
част/см3
, N
=3,6∙1020
част/см3
, N
 =1,8∙1020
част/см3
- начальные концентрации эпоксидных групп и аминогрупп отвердителя;
=1,8∙1020
част/см3
- начальные концентрации эпоксидных групп и аминогрупп отвердителя;
xэп
=0,8 – степень превращения эпоксидных групп в процессе отверждения;
n≈2 – среднее количество эпоксидных групп, связываемых одной аминогруппой отвердителя.
Решение:
Расходующаяся при титровании хлористоводородная (соляная) кислота затрачивается главным образом на нейтрализацию эпоксидных групп смолы (первое слагаемое главного соотношения) и на нейтрализацию первичных аминогрупп отвердителя (второе слагаемое).Количество подлежащих нейтрализации кислотой основных групп определяется разностью начальных количеств и прореагировавших количеств указанных функциональных групп:
V=3,6∙1020
 0,2∙1,4∙10-20
0,2∙1,4∙10-20
 (1,8∙1020
(1,8∙1020
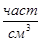 -
0,4∙3,6∙1020
-
0,4∙3,6∙1020
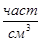 )×
)×
×3∙10-20
 =1,008
=1,008 +1,08 +1,08 =2,088 =2,088
Ответ:
V=2,088
8.Вычислить продолжительность 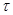 ,с заполнения глухих пор наполнителя эпоксидным связующим вязкостью ,с заполнения глухих пор наполнителя эпоксидным связующим вязкостью  =7 Па∙с. Средняя длина пор =7 Па∙с. Средняя длина пор 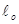 =10 мкм, глубина заполнения =10 мкм, глубина заполнения 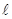 =7 мкм, внешнее давление P1
=8 МПа=8∙106
Па, начальное давление внутри поры P2
=105
Па (атмосферное давление), радиус пор R=1 нм. Расчёт провести по соотношению =7 мкм, внешнее давление P1
=8 МПа=8∙106
Па, начальное давление внутри поры P2
=105
Па (атмосферное давление), радиус пор R=1 нм. Расчёт провести по соотношению

Что является движущей силой процесса заполнения пор, закрытых с одного конца (глухих пор)? Сформулируйте закон, который выражается используемым соотношением.
Решение:
Относительное заполнение поры  < 1,поэтому < 1,поэтому 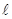 n n < 0 есть < 0 есть
величина отрицательная, поэтому  есть разность давлений внешнего и внутри поры, то есть движущая сила процесса заполнения поры. Таким образом, продолжительность заполнения поры пропорциональна вязкости жидкого полимера и обратно пропорциональна движущей силе процесса. Для заполнения поры на 7 мкм (70% полной глубины) потребуется есть разность давлений внешнего и внутри поры, то есть движущая сила процесса заполнения поры. Таким образом, продолжительность заполнения поры пропорциональна вязкости жидкого полимера и обратно пропорциональна движущей силе процесса. Для заполнения поры на 7 мкм (70% полной глубины) потребуется
 
Ответ:
τ=43 с
9.Вычислить толщину переходного слоя δ в системе, содержащей mсв
=13 г фенольного связующего при содержании наполнителя (лавсан) 60% масс., если массовая доля переходного слоя γ=0,34.Удельная поверхность наполнителя Sуд
=6 м2
/г, плотность связующего ρ=1,2 г/см3
. Расчёт вести по соотношению
δ=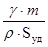 , ,
где m- масса связующего на 1 г наполнителя.
Что такое переходный слой и где он локализуется?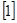
Решение:
Среднюю толщину переходного слоя δ определяют как отношение объёма V переходного слоя к его поверхности, принимаемой равной поверхности наполнителя S=Sуд
∙mнап
(1).
Масса наполнителя mнап
=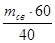 (2) (2)
Величина V= (3). С учетом соотношений (1-3) получаем: (3). С учетом соотношений (1-3) получаем:
δ=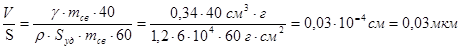
Ответ:
δ=0,03∙10-4
см=0,03 мкм
10. Методом обращенной газовой хроматографии (ОГХ) получено, что время удерживания τ паров этанола вискозной стренговой нитью (ВСН), помещенной в колонну хроматографа, составляет τ=50,5 с. Объемная скорость газа-носителя Vг
=0,3 мл/с. Объем V сорбированного нитью пара этанола вычислить по соотношению V=Vг
∙(τ-τо
)=Vг
∙Δτ (1), где τо
=15 с – время удерживания несорбируемого компонента (“мёртвое” время колонки).
Считая пары этанола идеальным газом, следует найти количество молей и количество частиц в объёме V. При расчете суммарной поверхности S волокон принять, что сорбированный этанол покрыл поверхность мономолекулярным слоем, а площадь, занимаемая одной молекулой этанола, составляет δ=20∙10-20 м2
. Найти удельную поверхность ВСН Sуд
= (2) при массе нити m=4,618 г. (2) при массе нити m=4,618 г.
Что называют молем? Что такое удельная поверхность твердого материала?
Назовите основные части и принцип работы газового хроматографа.
Решение:
Количество молей n сорбированных паров находим с использованием объема одного моля идеального газа 22400 мл/моль: n=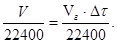
Количество сорбированных молекул N определяем через число Авогадро А=6,02∙1023
частиц/моль:
N=n∙A
Поверхность сорбции S определяем как площадь мономолекулярного слоя:
S=δN=δnA.
Отсюда удельная поверхность Sуд
:
Sуд
= = = = = = = = = ≈12,13 м2
/г ≈12,13 м2
/г
Ответ:
S=56 м2
; Sуд
≈12 м2
/г
11. Рассматривается процесс отверждения эпоксидной смолы ЭД-20.
Температурная зависимость изобарной мольной теплоёмкости этой смолы Ср
олиг
, Дж/моль∙К, определяется соотношением
Ср
олиг
=595+0,47Т+0,0002Т2
(1),
а температурная зависимость изобарной мольной теплоёмкости продукта с молекулярной массой 800 (димера) имеет вид
Ср
прод
 =7019-37,9Т+0,0607Т2
(2), то же для продукта с молекулярной массой 2000: Ср
прод
2000
=17290-93,4Т+0,15Т2
(3).
=7019-37,9Т+0,0607Т2
(2), то же для продукта с молекулярной массой 2000: Ср
прод
2000
=17290-93,4Т+0,15Т2
(3).
Вычислить тепловой эффект отверждения при 100°С, если при 30°С он составляет -122 кДж/моль, по соотношению:
Q373
=Q303
+Δαo
(373-303)+ Δα1
(3732
-3032
)+ Δα1
(3732
-3032
)+ Δα2
(3733
-3033
) (4) Δα2
(3733
-3033
) (4)
Решение:
В данной задаче рассматриваются две модельные реакции
2 Ол. Прод 800
(I) Прод 800
(I)
5 Ол. Прод2000
(II), Прод2000
(II),
где Ол.- исходный олигомер со средней молекулярной массой 400.
В соответствии с правилами термодинамики величины Δαi
рассчитываются по соотношениям:
Δαi
=αi
прод 800
- 2αi
 для реакции (I) и
для реакции (I) и
Δαi
=αi
прод 2000
- 2αi
 для реакции (II)
для реакции (II)
1.Расчёт теплового эффекта реакции (I) при 373К:
Δαo
=7019-2∙595=5829
Δα1
=-37,9-2∙0,466=-38,832
Δα2
=0,061- 0,00042=0,0605,
При этом обязателен учет знака коэффициентов αi
:
Q373
=-122000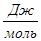 +5829∙70-19,416∙47320+0,02∙24076990=- 122000Дж/моль-29195 Дж/2 моль = -122000 Дж/моль –14597 Дж/моль ≈-137 кДж/моль +5829∙70-19,416∙47320+0,02∙24076990=- 122000Дж/моль-29195 Дж/2 моль = -122000 Дж/моль –14597 Дж/моль ≈-137 кДж/моль
2.Расчёт теплового эффекта реакции (II) при 373 К:
∆αo
=17290-5∙595=17290-2975=14315
∆α1
=-93,36-5∙0,466=-93,36-2,33=-95,69
∆α2
=0,15- 0,00021∙5=0,15-0,00105=0,14895
Q373
=-122000+(14317∙70-0,5∙95,69∙47320+0,33∙0,14895∙24076990)=-122000+(1002190-2264025+1177112)=-122000+(2179302-2264025)=-122000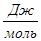 - -
-84723Дж/5моль=-122000 Дж-16945Дж ≈139 кДж/моль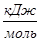
Ответ
: Q373
=-122-15=-137 кДж/моль
Q373
=-122-17=-139 кДж/моль
13. Найти поверхность S наполнителя в образце массой m=21,6 г при соотношении связующего и наполнителя 3:2 по массе, если в качестве наполнителя использована капроновая нить с удельной поверхностью Sуд
=10 м2
/г
Решение:
Материал содержит две массовые части из пяти, то есть 40% масс.
Следовательно , масса наполнителя mнап
=21,6∙0,4=8,64 г.Суммарная поверхность S всех макрочастиц наполнителя
S=mнап
∙Sуд
=8,642∙10 =86,4 м2 =86,4 м2
Ответ:
S=86,4 м2
14. Найти во сколько раз кажущаяся поверхность Sрасч
капроновой нити толщиной Т=2 текс, состоящей из 50 элементарных волокон, отличается от удельной поверхности Sуд
=10 м2
/г, плотность капрона ρ=1,14 г/см3
. Элементарные волокна считать круглыми цилиндрами с поперечным сечением F= мкм2
.Почему удельная (истинная) поверхность значительно больше кажущейся (расчётной) поверхности? мкм2
.Почему удельная (истинная) поверхность значительно больше кажущейся (расчётной) поверхности?
Решение:
Общее сечение нити F= = = =1754 мкм2 =1754 мкм2
Сечение элементарного волокна Fвол
= =35 мкм2 =35 мкм2
Условный радиус элементарного волокна r = 3,34 мкм= 3,34 мкм=
=3,34∙10-6 м.
Из сущности определения толщины в тексах: 2 г – 1000 м
1 г – 500 м =
Поверхность круглого элементарного волокна определяется в основном как поверхность круглого цилиндра: S= =6,28∙3,34∙10-6
м∙500 м = =6,28∙3,34∙10-6
м∙500 м =
=21∙500∙10-6
м2
=10488∙10-6
м2
=0,0104876 м2
≈0,0105 м2
Sрасч
=nS=0,0104 м2
∙50=0,52 м2
/г
Искомое отношение Sуд
/Sрасч
= ≈19 ≈19
Большое отличие Sуд
от Sрасч
обусловлено тем, что при вычислении Sрасч
не учитывали дефекты поверхности.
Ответ:
 ≈19 ≈19
15. Исходя из выражений для средней степени превращения связующего в композиции x=xсв
(1-γ)+yγ (1) и степени превращения связующего в переходном слое y=xсв
+χ (2), вывести соотношение для вычисления параметра влияния χ (xсв
- степень превращения связующего в объёме, γ- массовая доля связующего,образовавшего переходный слой).
Решение:
Подставив соотношение (2) в соотношение (1), получаем:
X=xсв
-γxсв
+γxсв
+χγ
Отсюда χ=
Ответ
: χ=
17. Степень превращения связующего y в переходном слое больше степени превращения связующего в объёме xсв
на 0,18: y-xсв
=χ=0,18. Пользуясь соотношением χ=(x-xсв
)/γ=∆x/γ, найти массовую долю γ связующего, образовавшего переходный слой, если из кинетических результатов получено ∆x=0,10 (x-средняя степень превращения связующего в материале).Каково в этом случае влияние наполнителя на кинетику отверждения?
Решение:
Из соотношения χ=(x-xсв
)/γ получаем : γ= =0,55. =0,55.
Из соотношений y>xсв
, χ=y-xсв
>0 видно, что степень превращения в переходном слое выше, чем в объёме, то есть наполнитель ускоряет отверждение.
Ответ:
γ=0,55. Наполнитель ускоряет отверждение.
16. Найти скорость диффузии U=Δx/τ олигомерных молекул фенолоформальдегидной смолы к поверхности наполнителя по кинетическим данным:
| τ,мин |
x,масс.
доли
|
xсв
,масс.
доли
|
Δx=x-xсв
|
(U,с-1
)∙
∙105
|
γ |
χ= |
| 30 |
0,33 |
0,30 |
| 60 |
0,67 |
0,60 |
| 90 |
0,90 |
0,80 |
| 120 |
0,92 |
0,84 |
| 150 |
0,94 |
0,88 |
| 180 |
0,95 |
0,91 |
| 210 |
0,96 |
0,94 |
| 240 |
0,97 |
0,96 |
Принято, что отверждение протекает в диффузионной области.Построить на миллиметровой бумаге график зависимости U(τ).Путем графического интегрирования графика U(τ) найти значения γ:
γτ
= и вычислить значение параметра влияния χ.Заполните таблицу. и вычислить значение параметра влияния χ.Заполните таблицу.
Решение:
Величина U=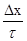 есть по существу скорость физико-химического взаимодействия между наполнителем и связующим.Для вычисления U продолжительность отверждения τ следует выразить в секундах. Величины Δx и U проходят через максимум, поэтому график U(τ) имеет экстремальную форму. Для графического интегрирования графика U(τ) необходимо: есть по существу скорость физико-химического взаимодействия между наполнителем и связующим.Для вычисления U продолжительность отверждения τ следует выразить в секундах. Величины Δx и U проходят через максимум, поэтому график U(τ) имеет экстремальную форму. Для графического интегрирования графика U(τ) необходимо:
1) определить количество массовых долей, приходящихся на 1 см2
площади графика – найти “цену” С одного квадратного сантиметра площади, ограниченной данным графиком;
2) выразить в квадратных сантиметрах площади Si
полос, соответствующих продолжительности процесса 30;60;90;120;150;180;210;240 минут;
3) величинаγ1
=СS1
; γ2
=C(S1
+S2
); γ3
=C(S1
+S2
+S3
)…. γ8
=C
Значения параметра влияния χ >1 не имеет реального смысла и обусловлены погрешностью данного метода расчёта.
Ответ:
γmax
=0,14; χmax
=0,70
17. Определить среднюю толщину δ переходного слоя, образованного фенолоформальдегидным связующим массой m=12,96 г на поверхности S=86,4 м2
при массовой доле γ связующего, образовавшего переходный слой, γ=0,56. Плотность фенолоформальдегидного связующего ρ=1,2 г/см3
.
Решение:
Средняя толщина переходного слоя определяется отношением объёма υ переходного слоя к его площади S:
δ= 0,07∙10-4
см=0,07 мкм 0,07∙10-4
см=0,07 мкм
Фенолформальдегидная смола образует на поверхности волокнистых наполнителей сравнительно тонкие переходные слои: 0,03 мкм – на поверхности лавсана (задача 9), 0,07 мкм – на поверхности капрона (задача 17).
Ответ:
δ=0,07 мкм
18.Определить концентрации непрореагировавших олигомеров в объёме связующего С1
и в переходном слое С2
, а также их разность ∆С=С2
-С1
(движущую силу диффузии), если xсв
=0,80; χ=0,17;γ=0,56.Общая масса связующего m=12,96 г. Расчет вести по модели 1 (см. рис.1):

Рис.1 Схема переходного слоя по модели 1

Плотность связующего ρ=1,2 г/см3
.
В какую сторону диффундируют олигомерные молекулы в соответствии с полученными результатами ? Найти движущую силу диффузии ΔС=С2
-С1
.
Решение:
С1
~ 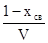 (1), С2
~ (1), С2
~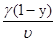 (2), где V- объём связующего, υ- объём переходного слоя. (2), где V- объём связующего, υ- объём переходного слоя.
V=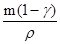 (3), υ= (3), υ= (4), y=xсв
+χ (5). (4), y=xсв
+χ (5).
Подставляя (3), (4), (5) в (1) и (2), получаем:
C1
= масс. доли/см3
=см-3 масс. доли/см3
=см-3
С2
= =0,00280 см-3 =0,00280 см-3
∆С=С2
-С1
=0,00280-0,04209=-0,03929≈-0,0393 см-3
Ответ:
∆С=-0,0393 см-3
; олигомерные молекулы диффундируют из объёма связующего к поверхности наполнителя, т.к наполнитель ускоряет отверждение.
19. Определить среднюю толщину δ переходного слоя, образованного эпоксидным связующим массой m=12,96 г на поверхности наполнителя S=86,4 м2
при массовой доле связующего,образовавшего переходный слой,γ=0,90.Плотность эпоксидного связующего ρ=1,2 г/см3
.
Решение:
Среднюю толщину переходного слоя можно оценить как отношение объёма переходного слоя υ к его поверхности S:
Δ= 0,1125∙10-4
см=0,1125 мкм 0,1125∙10-4
см=0,1125 мкм
Ответ:
δ=0,1125∙10-4
см=0,1125 мкм
20. Вычислить коэффициент диффузии D, олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон используя соотношение U=-DS(∆C/δ) (первый закон Фика), где скорость диффузии U=1,85∙10-5
с-1
, движущая сила диффузии ∆С=-0,0393 см-3
, толщина переходного слоя δ=0,07 мкм, площадь переходного слоя (поверхность диффузии) S=86,4 м2
. S выразить в см2
, δ- в см
Решение:
Из данного выражения первого закона Фика в конечных приращениях следует :
D1
=- 0,0382∙10-13 0,0382∙10-13
 =3,82∙10-15
см2
/с.
=3,82∙10-15
см2
/с.
Порядок полученной величины D1
соответствует известным значениям коэффициентов диффузии молекул низкомолекулярных веществ в твёрдых полимерах.
Ответ:
D1
=3,82∙10-15
см2
/с
21. Вычислить коэффициент диффузии D2
олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон, используя соотношение  (второй закон Фика), где толщина переходного слоя (путь диффузии) δ=0,07 мкм, продолжительность процесса Δτ=90 мин. (необходимо Δτ выразить в секундах). (второй закон Фика), где толщина переходного слоя (путь диффузии) δ=0,07 мкм, продолжительность процесса Δτ=90 мин. (необходимо Δτ выразить в секундах).
Решение:
Величины движущей силы диффузии ΔС=С2
-С1
в левой и правой частях выражения для второго закона Фика в конечных приращениях сокращаются, поэтому указанное выражение принимает вид  , ,
откуда D2
= . .
Порядок величины D2
совпадает с порядком коэффициента диффузии D1
, полученного в задаче 20 с использованием первого закона Фика. В принципе коэффициент диффузии в в обоих законах Фика – одна и та же величина.
Ответ:
D2
=8,98∙10-15
см2
/с
22. Вычислить коэффициент диффузии D1
олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон, используя соотношение U=-D1
S(ΔC/δ) (первый закон Фика),где скорость диффузии U=1,85∙10-5
с-1
, движущая сила диффузии ΔС=0,0377 см-3
, толщина переходного слоя δ=0,07 мкм, площадь переходного слоя (поверхность диффузии) S=86,4 м2
. S выразить в см2
, δ- в см.
В данной задаче величина ΔС определена на основе модели 2 переходного слоя (рис.2)
 
Рис.2 Схема переходного слоя по модели 2
Решение:
D1
= 3,98∙10-15 3,98∙10-15

Ответ:
D1
=3,98∙10-15
см2
/с
23. Вычислить коэффициент диффузии D2
олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон,используя соотношение  (второй закон Фика), где ΔС – движущая сила диффузии, δ=0,07 мкм – толщина переходного слоя (путь диффузии), Δτ=90 мин. – продолжительность диффузии. (второй закон Фика), где ΔС – движущая сила диффузии, δ=0,07 мкм – толщина переходного слоя (путь диффузии), Δτ=90 мин. – продолжительность диффузии.
Следует δ выразить в см, τ- в секундах.
Решение:
Из данного выражения второго закона Фика в конечных приращениях получаем:
D2
=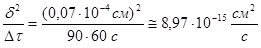
Из сравнения задач 21 и 23 следует, что при нахождении коэффициента диффузии с использованием второго закона Фика получаемое значение в не зависит от того, по какой модели переходного слоя рассчитывают величину ΔС, т.е величина ΔС в этом случае не имеет большого значения.
Ответ:
D2
=8,97∙10-15
см2
/с
24. Используя приведённые кинетические данные зависимости степени превращения xсв
ненаполненного эпоксидного связующего и степени превращения такого же связующего в смеси с волокнистым наполнителем (нить лавсан) от продолжительности отверждения τ, найти скорость U= взаимодействия между наполнителем и связующим. Графическим интегрированием зависимости U(τ) найти массовые доли γ связующего,образовавшего переходные слои γ= взаимодействия между наполнителем и связующим. Графическим интегрированием зависимости U(τ) найти массовые доли γ связующего,образовавшего переходные слои γ=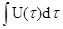 : :
| τ,мин |
x,масс.
доли
|
xсв
,масс.
доли
|
Δx=x-xсв
|
(U,с-1
)∙
∙105
|
γ |
χ= |
| 30 |
0,51 |
0,30 |
| 60 |
0,72 |
0,47 |
| 90 |
0,80 |
0,64 |
| 120 |
0,86 |
0,70 |
| 150 |
0,90 |
0,75 |
| 180 |
0,93 |
0,80 |
| 210 |
0,94 |
0,84 |
| 240 |
0,94 |
0,86 |
Вычислить также параметр влияния χ и указать, чему равна скорость диффузии олигомерных молекул связующего к поверхности элементов наполнителя, если отверждение протекает в диффузионной области.
Решение:
Для вычисления и U продолжительность отверждения τ следует выразить в секундах. Величины Δx и U проходят через максимум, поэтому график U(τ) имеет экстремальную форму. Для графического интегрирования графика U(τ) необходимо:
1) определить количество массовых долей, приходящихся на 1 см2
площади графика – найти “цену” С одного квадратного сантиметра площади, ограниченной данным графиком;
2) выразить в квадратных сантиметрах площади Si
полос, соответствующих шагу Δτ=30 мин. при изменении τ от 0 до 240 минут (рис.3);
3) величинаγ1
=CS1
, γ2
=С(S1
+S2
), γ3
=C(S1
+S2
+S3
), ….. γ8
=С=
Значения параметра влияния χ>1 не изменяют реального смысла и обусловлены погрешностью данного метода расчёта.
Сравнение результатов задач 24 и 16 показывает, что эпоксидное связующее образует более толстые (массивные) переходные слои, чем феноло-формальдегидное связующее (значения γmax
составляют 0,63 и 0,14 соответственно). При этом в переходных слоях эпоксидного связующего выше роль химического взаимодействия между связующим и наполнителем (χmax
составляет 0,96 и 0,70 соответственно).
Скорость диффузии олигомерных молекул связующего равны скорости U взаимодействия между связующим и наполнителем, если отверждение протекает в диффузионной области.
Ответ: γmax
=0,63 χmax
=0,96
25. Определить концентрации (массовые доли/см3
) непрореагировавших олигомеров в объёме связующего С1
и в переходном слое С2
, если степень превращения в объёме xсв
=0,64; χ=0,35; γ=0,34. Общая масса связующнго m=12,96 г. Расчёт вести по модели 1 (то есть всё связующее, находящееся вблизи поверхности наполнителя, считать относящимся к переходному слою). Плотность связующего ρ=1,2 г/см3
.
Найти движущую силу ΔС диффузии олигомерных молекул связующего в системе связующее-наполнитель. В какую сторону диффундируют олигомерные молекулы в данной задаче?
Решение:
Концентрацию С1
олигомеров в объёме связующего V можно оценить как массовую долю олигомеров в единице объёма: С~ . .
Аналогично концентрация в олигомеров в переходном слое С2
~ , ,
где степень превращения связующего в переходном слое y=xсв
+χ=0,99.
Принимая плотности связующего в объёме и в переходном слое равными, можно вычислить объёмы:
V= =7,128 см3
; =7,128 см3
;
υ = =3,672 см3 =3,672 см3
Используя приведённые соотношения, получаем:
C1
=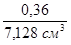 =0,05050 см-3 =0,05050 см-3
С2
= 0,000926 см-3
; 0,000926 см-3
;
ΔC=C2
-C1
=-0,004957 см-3
Самодиффузия протекает в направлении от большей концентрации к меньшей, то есть из объёма к поверхности наполнителя, ускоряющего отверждение.
Ответ:
С1
=0,005050 см-3
, С2
=0,000926 см-3
, ΔС=С2
-С1
=-0,04957 см-3
26. Определить концентрации (массовые доли/см3
) непрореагировавших олигомеров в объёме связующего С1
и в переходном слое С2
,если степень превращения в объёме xсв
=0,64; χ=0,35; γ=0,34. Общая масса связующего m=12,96 г.Расчёт вести по модели 2 (то есть к переходному слою относить только отвержденные участки, находящиеся вблизи поверхности элементов наполнителя), при этом объём переходного слоя υ=myγ/ρ несколько сократится по сравнению с расчётом по модели 1 (y=xc
в
+χ – cтепень превращения олигомеров в переходном слое). Плотность связующего ρ=1,2 г/см3
.
Найти движущую силу ΔС диффузии олигомерных молекул связующего в системе связующее-наполнитель.В какую сторону диффундируют олигомерные молекулы в данной задаче?
Решение:
По аналогии с задачей 25 концентрацию С1
олигомеров в объёме связующего V можно оценить как массовую долю олигомеров в единице объёма: C1
~ , концентрацию С2
олигомеров в переходном слое объёмом υ : С2
~ , концентрацию С2
олигомеров в переходном слое объёмом υ : С2
~ , где степень превращения связующего в переходном слое y=xсв
+χ=0,99. , где степень превращения связующего в переходном слое y=xсв
+χ=0,99.
Принимая плотности связующего в объёме и в переходном слое равными, можно вычислить объёмы, исключив из переходных слоев неотвержденные участки (в соответствии с моделью 2):
V= =7,165 см3
; =7,165 см3
;
υ=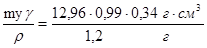 =3,635 см3 =3,635 см3
Используя вышеуказанные соотношения, получаем:
C1
= =0,0524 см-3 =0,0524 см-3
С2
=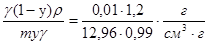 =0,000935 см-3 =0,000935 см-3
ΔС=0,000935-0,05024=-0,04931 см-3
Таким образом, различие между величинами ΔС, рассчитанными при использовании моделей 1 и 2, невелико (см. задачу 25), так как при y 1 различие между моделями 1 и 2 сглаживается. 1 различие между моделями 1 и 2 сглаживается.
Ответ:
С1
=0,05024 см-3
; С2
=0,000935 см-3
; ΔС=С2
-С1
=-0,04931 см-3
.
27. Вычислить коэффициент диффузии D1
олигомерных молекул эпоксидного связующего к поверхности волокна лавсан в процессе отверждения, используя соотношение U=-D1
S(ΔC/δ) (первый закон Фика), где U=3,00∙10-5
масс. доли/с- скорость диффузии олигомеров, численно равная скорости взаимодействия связующего и наполнителя в диффузионной области; ΔС=-0,04957 масс.доли/см3
- движущая сила диффузии, рассчитанная по модели 1 переходного слоя; масса полимерного образца m=21,6 г.; содержание наполнителя Снап
=40 масс.%, удельная поверхность волокнистого наполнителя Sуд
=6 м2
/г; толщина переходного слоя δ=2 мкм.
Решение:
Величину коэффициента диффузии D1
находим из данного выражения для первого закона Фика:
D1
=- , где S- поверхность диффузии, которую принимаем равной поверхности наполнителя: , где S- поверхность диффузии, которую принимаем равной поверхности наполнителя:
S=mCнап
Sуд
=21,6 г ∙0,4∙6 м2
/г=51,84∙104
см2
.
Используя полученное значение S, имеем:
D1
= ≈2,33∙10-13
см2
/с ≈2,33∙10-13
см2
/с
Ответ:
D1
=2,33∙10-13
см2
/с
28. Вычислить коэффициент диффузии D2
олигомерных молекул эпоксидного связующего к поверхности волокна – наполнителя лавсан в процессе отверждения, используя соотношение 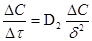 (второй закон Фика), где движущая сила диффузии ΔС=-0,04957 масс. доли/см3
рассчитана по модели 1 переходного слоя, толщина переходного слоя (путь диффузии) δ=2 мкм; продолжительность отверждения Δτ=90 мин. при атмосферном давлении. (второй закон Фика), где движущая сила диффузии ΔС=-0,04957 масс. доли/см3
рассчитана по модели 1 переходного слоя, толщина переходного слоя (путь диффузии) δ=2 мкм; продолжительность отверждения Δτ=90 мин. при атмосферном давлении.
Решение:
В соответствии с данным выражением второго закона Фика величина движущей силы ΔС не играет существенной роли при вычислении D2
:
D2
=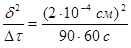 =7,40∙10-12
см2
/с=74∙10-13
см2
/с =7,40∙10-12
см2
/с=74∙10-13
см2
/с
Получено ,что D2
примерно в 30 раз больше, чем D1
(cм. Задачу 27):
 =31,8 =31,8
Ответ:
D2
=7,40∙10-12
см2
/с
29. Вычислить коэффициент диффузии D1
олигомерных молекул эпоксидного связующего к поверхности волокна лавсан в процессе отверждения, используя соотношение U=-D1
S(ΔC/δ) (первый закон Фика), где U=3,00∙10-5
масс. доли/с – скорость диффузии олигомеров, численно равная скорости взаимодействия связующего и наполнителя в диффузионной области;ΔС=-0,04931 масс.доли/см3
– движущая сила диффузии, рассчитанная по модели 2 переходного слоя; масса полимерного образца m=21,6 г; содержание наполнителя Снап
=40% масс., удельная поверхность волокнистого наполнителя Sуд
=6 м2
/ч; толщина переходного слоя δ=2 мкм.
Решение:
Величину коэффициента диффузии D1
находим из данного в условии выражения для первого закона Фика:
D1
=- , где S – поверхность диффузии, которую принимаем равной поверхности наполнителя: S=m∙Cнап
∙Sуд
=21,6 г∙0,4∙6 , где S – поверхность диффузии, которую принимаем равной поверхности наполнителя: S=m∙Cнап
∙Sуд
=21,6 г∙0,4∙6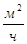 =51,8∙104
м2
используя полученное значение S, имеем: =51,8∙104
м2
используя полученное значение S, имеем:
D1
= ≈2,35∙10-13
см2
/с ≈2,35∙10-13
см2
/с
При использовании ΔС, рассчитанной по модели 1 переходного слоя, имели незначительное отличие величины D1
(cм. Задачу 27):
D1
=2,33∙10-13
см2
/с.
Ответ:
D1
=2,35∙10-13
см2
/с.
30. Вычислить коэффициент диффузии D2
олигомерных молекул эпоксидного связующего к поверхности волокна – наполнителя лавсан в процессе отверждения, используя соотношение 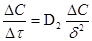 (второй закон Фика), где движущая сила диффузии ΔС=-0,04931 масс.доли/см3
рассчитана по модели 2 переходного слоя, толщина переходного слоя (путь диффузии) δ=2 мкм; продолжительность отверждения при атмосферном давлении Δτ=90 мин. (второй закон Фика), где движущая сила диффузии ΔС=-0,04931 масс.доли/см3
рассчитана по модели 2 переходного слоя, толщина переходного слоя (путь диффузии) δ=2 мкм; продолжительность отверждения при атмосферном давлении Δτ=90 мин.
Решение:
Из данного в условии задачи соотношения получаем: D2
=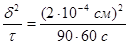 =7,34∙10-12
см2
/с =7,34∙10-12
см2
/с
Сравнение результатов расчетов коэффициентов диффузии в задачах 27-30 по моделям 1,2 переходных слоёв:
D11
=2,33∙10-13
см2
/с; D12
=2,35∙10-13
см2
/с
D21
=7,40∙10-12
см2
/с; D22
=7,34∙10-12
см2
/с
показывает,что использование различных моделей переходных слоёв обусловливает меньшее различие в величине коэффициентов диффузии, чем использование различных законов диффузии.
Решение:
D2
=7,34∙10-12
см2
/с.
31. Определить среднюю толщину 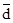 прослойки эпоксидного связующего между волокнами, зная путь прослойки эпоксидного связующего между волокнами, зная путь 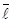 диффундирующих молекул в момент времени τ1
, когда разбавляющее и замедляющее влияние волокнистого наполнителя компенсировано физико-химическим взаимодействием между связующим и наполнителем: диффундирующих молекул в момент времени τ1
, когда разбавляющее и замедляющее влияние волокнистого наполнителя компенсировано физико-химическим взаимодействием между связующим и наполнителем:
   Х 1 1- с наполнителем; 2 – без наполнителя; Х 1 1- с наполнителем; 2 – без наполнителя;
   2 2
 τ τ
(x- cтепень превращения олигомерной термореактивной смолы в сетчатый продукт)
При расчёте исходить из того, что 2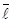 =d, и использовать соотношение D= =d, и использовать соотношение D= 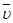 ∙ ∙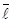 , где D=6,0∙10-12
см2
/с – коэффициент диффузии олигомерных молекул смолы, , где D=6,0∙10-12
см2
/с – коэффициент диффузии олигомерных молекул смолы, 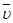 =10-7
см/с – средняя линейная скорость диффундирующих олигомерных молекул в рассматриваемом направлении. =10-7
см/с – средняя линейная скорость диффундирующих олигомерных молекул в рассматриваемом направлении.
Решение:
Из данного в условии задачи соотношения D= 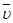 ∙ ∙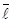 = = 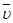 ∙ ∙ cледует: cледует:
 = =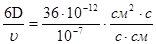 =36∙10-5
см=3,6∙10-4
см=3,6 мкм =36∙10-5
см=3,6∙10-4
см=3,6 мкм
Ответ:
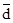 =3,6∙10-4
см=3,6 мкм =3,6∙10-4
см=3,6 мкм
32. Вывести в общем виде выражение для движущей силы ΔС диффузии олигомерных молекул в системе связующее-наполнитель, используя модель 1 переходного слоя, через параметры y,γ,χ (y-cтепень превращения связующего в сетчатый продукт в переходном слое); γ-массовая доля связующего, образовавшего переходный слой; y=xсв
+χ, где xсв
- cтепень превращения связующего в объёме; χ-параметр влияния. При выводе исходить из того, что ΔС=С2
-С1
– движущая сила диффузии определяется разностью концентраций олигомеров в переходном слое С2
и в объёме С1
.Концентрации определяются как отношение массовых долей олигомеров в переходном слое и в объёме связующего к соответствующим объёмам υ и V (γ(1-y)-количество олигомеров в переходном слое по модели 1).
Решение:
ΔС=С2
-С1
=
Учитывая, что  =V, получаем: =V, получаем:
ΔС=
Используя соотношение y=xсв
+χ, окончательно имеем:
ΔC=
Ответ:
ΔС=-
33. Вывести в общем виде выражение для движущей силы ΔС диффузии олигомерных молекул в системе связующее с массой и плотностью ρ – наполнитель, используя модель 2 переходного слоя, через параметры y,γ,χ (y-степень превращения связующего в сетчатый продукт в переходном слое; γ- массовая доля связующего, образовавшего переходный слой; y=xсв
+χ, где xсв
- степень превращения связующего в объёме; χ-параметр влияния. При выводе исходить из того, что ΔС=С2
-С1
– движущая сила диффузии определяется разностью концентраций олигомеров в переходном слое С2
и в объёме С1
. Концентрация определяется как отношение массовых долей олигомеров в переходном слое и в объёме связующего к соответствующим объёмам υ и V (γ(1-yγ)- количество олигомеров в переходном слое по модели 2).Общий объём связующего V определяется его массой m и плотностью ρ: V=m/ρ.
Решение:
ΔС=С2
-С1
=
Учитывая соотношение υ/γ=V, y=xсв
+χ, получаем:
ΔC=
Ответ:
ΔС= = =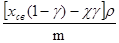
34. Используя аддитивность тепловых эффектов отверждения ненаполненного эпоксидного связующего Q и взаимодействие Qдоп
эпоксидного связующего с лавсаном, из которых складывается тепловой эффект суммарного процесса Qсумм
=γQдоп
+(1-γ)Q, найти величину Qдоп
, если Qсумм
=104 кДж/моль, Q=122 кДж/моль; массовая доля связующего, образовавшего переходный слой, γ=0,63.
Решение:
Выразив аддитивность тепловых эффектов отверждения ненаполненного эпоксидного связующего Q и взаимодействии Qдоп
эпоксидного связующего с лавсаном, из которых складывается тепловой эффект суммарного процесса Qсумм
=γQдоп
+(1-γ)Q, найти величину Qдоп
, если Qсумм
=104 кДж/моль, Q=122 кДж/моль; массовая доля связующего, образовавшего переходный слой , γ=0,63.
Выразив Qдоп
из соотношения, приведённого в условии задачи, и подставив численные значения величин, получаем:
Qдоп
=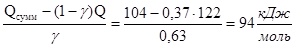
Ответ:
Qдоп
=94 кДж/моль
35. На основании известных экспериментальных значений тепловых эффектов отверждения эпоксидной смолы без наполнителя
Q=-122 кДж/моль, отверждения эпоксидной смолы с полипропиленовой нитью Qсумм
=-132 кДж/моль и эффективных энергий активации, кДж/моль, отверждения эпоксидной смолы без наполнителя Е=27, эпоксидной смолы с полипропиленовой нитью Есумм
=100 найти значения параметров А и В соотношения Е=А+В|Q|, считая, что значения А и В одинаковы для отверждения ненаполненных и наполненных систем.
Решение:
Применив зависимость Е от |Q| для ненаполненной и наполненной эпоксидной смолы, получаем систему двух линейных уравнений с двумя неизвестными:
27=А+122В
100=А+132В,
Откуда имеем: А=27-122В; 100=27-122В+132В;
10В=73; В=7,3
А=27-122∙7,3=-863,6≈-864 кДж/моль
Ответ:
А=-864 кДж/моль; В=7,3.
36. Из соотношения Qдоп
=200χ+20(1-χ) найти значения параметра влияния χ на основании известных значений теплового эффекта Qдоп
взаимодействия между связующим и наполнителем для систем: эпоксидная смола ЭД-20 и полипропиленовая нить (ППН), анилино-фенолоформальдегидная смола СФ-342А и ППН-180 и 50 кДж/моль соответственно.
Решение:
Из данного в условии задачи соотношения следует, что тепловой эффект взаимодействия между связующим и наполнителем аддитивно складывается из теплоты химического (первое слагаемое) и физического (второе слагаемое) взаимодействия. Из этого соотношения следует: 180χ=Qдоп
-20; χ= . .
Применив последнее соотношение к смолам ЭД-20 и СФ-342А, получаем соответственно: χ1
= =0,89; χ2
= =0,89; χ2
= =0,17 =0,17
Из полученных значений χ1
>χ2
следует, что при взаимодействии наполнителя ППН со смолой ЭД-20 преобладают химические процессы, а при взаимодействии ППН со смолой СФ-342А- физические.
Ответ:
χ1
=0,89; χ2
=0,17
37. Используя аддитивность тепловых эффектов отверждения ненаполненного связующего Q и взаимодействия Qдоп
связующего с полипропиленовым наполнителем (ППН)
Qсумм
=γQдоп
+(1-γ)Q, вычислить массовые доли γ переходных слоев в системах эпоксидная смола+ППН (Q=122; Qc
умм
=132; Qдоп
=180 кДж/моль) и фенолоформальдегидная смола+ППН (Q=21; Qсумм
=23; Qдоп
=50 кДж/моль) и толщину переходных слоёв δ= в тех же системах в тех же системах
(m=32 г- масса смолы на 1 г. наполнителя, ρ=1,2 г/см3
- плотность связующего, она практически одинакова для обеих рассматриваемых смол; Sуд
=5 м2
/г- удельная поверхность полипропиленовой нити, используемой в качестве наполнителя).
С каким связующим ППН образует более толстые и прочные переходные слои?
Решение:
Из данного в условии соотношения аддитивности тепловых эффектов выражаем величину γ:
γ = 
Подставляя в это соотношение численные значения тепловых эффектов, получаем для двух связующих:
γ1
=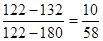 =0,172 =0,172
γ2
= =0,069 =0,069
Затем вычисляем соответственно среднюю толщину переходных слоёв
δ1
= =0,92∙10-4
см=0,92 мкм =0,92∙10-4
см=0,92 мкм
δ2
= 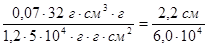 =0,37∙10-4
см=0,37 мкм =0,37∙10-4
см=0,37 мкм
При взаимодействии ППН с эпоксидной смолой выделяется больше теплоты, чем при взаимодействии ППН с фенолоформальдегидной смолой:
180>50 кДж/моль. Таким образом, эпоксидная смола образует более толстые 0,92>0,37 мкм и прочные переходные слои.
Ответ:
γ1
=0,172; δ1
=0,92 мкм;
γ2
=0,069; δ2
=0,37 мкм.
38. Используя аддитивность тепловых эффектов отверждения Q ненаполненной анилино-фенолоформальдегидной смолы СФ-342А и взаимодействия Qдоп
этой смолы с лавсаном, из которых складывается тепловой эффект суммарного процесса Qсумм
=γQдоп
+(1-γ)Q, найти величину Qдоп
, если Qсумм
=65 кДж/моль, Q=21 кДж/моль; массовая доля связующего, образовавшего переходный слой, γ=0,56
Решение:
Из балансового уравнения тепловых эффектов, данного в условии задачи, находим:
Qдоп
= ≈100 кДж/моль ≈100 кДж/моль
Отверждение анилино-фенолоформальдегидной смолы при повышенных давлениях ускорится капроном, тепловой эффект взаимодействия капрона с этим связующим сравнительно велик, величина Qдоп
=100 кДж/моль близка к прочности химических связей между связующим и наполнителем.
Ответ:
Qдоп
=100 кДж/моль
39. На основании известных экспериментальных значений эффективной энергии активации отверждения смеси анилино-фенолоформальдегидной смолы СФ-342А с капроном Есумм
=101 кДж/моль и суммарного теплового эффекта отверждения указанной смеси Qсумм
=-65 кДж/моль. Найти параметр А соотношения Е=А+В|Q|.Параметр В=7,3 считать одинаковым для смол СФ-342А и эпоксидной ЭД-20.
Решение:
Из соотношения зависимости Е от |Q| выражаем :
А=Е-В|Q|=101-7,3∙65=101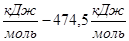 =-374 кДж/моль. =-374 кДж/моль.
Указанное соотношение является уравнением прямой, в котором В-тангенс угла наклона прямой, А-значение Е при |Q|=0, то есть точка пересечения прямой с осью Е.
Ответ:
А= - 374 кДж/моль.
40. Используя соотношение между энергией активации Е и тепловым эффектом Q; Е= - 864+7,3|Q| для отверждения эпоксидной смолы ЭД-20, вычислить абсолютные значения |Qдоп
|, кДж/моль тепловых эффектов взаимодействия ЭД-20 с лавсаном и ППН, если энергии активации Едоп
этих процессов составляют 43 и 172 кДж/моль соответственно.
Решение:
Выразим величину |Q| из данного соотношения: |Q|= . .
Применяя это соотношение к процессу взаимодействия между связующим и различными наполнителями, получаем для лавсана:
|Qдоп
 |=
|= =124 кДж/моль =124 кДж/моль
и для полипропиленовой нити:
|Qдоп
 |=
|= =142 кДж/моль =142 кДж/моль
Полученные значения |Qдоп
 | и |Qдоп
| и |Qдоп
 | свидетельствуют о том, что эпоксидная смола образует с полипропиленом более прочные химические связи, чем с лавсаном.
| свидетельствуют о том, что эпоксидная смола образует с полипропиленом более прочные химические связи, чем с лавсаном.
Ответ: |Qдоп
 |=124 кДж/моль
|=124 кДж/моль
|Qдоп
 |=142 кДж/моль
|=142 кДж/моль
41. Используя соотношение Е=-374+7,3|Q| между энергией активации Е и тепловым эффектом Q для отверждения анилино-фенолоформальдегидной смолы СФ-342А, вычислить абсолютные значения |Qдоп
|,кДж/моль, тепловых эффектов взаимодействия смолы СФ-342А с ППН при повышенном (8 МПа) и атмосферном давлении, если энергии активации этих процессов Едоп
составляют 34 и 21 кДж/моль соответственно.
Решение:
Выразим величину |Q| из данного в условии соотношения: |Q|= . .
Применив это соотношение к процессу взаимодействия между связующим и наполнителем, получаем величины |Qдоп
 | при повышенном и |Qдоп
| при повышенном и |Qдоп
 | при атмосферном давлении соответственно:
| при атмосферном давлении соответственно:
|Qдоп
 |=
|= =56 кДж/моль, =56 кДж/моль,
|Qдоп
 |=
|= =54 кДж/моль. =54 кДж/моль.
Полученные значения показывают, что величина давления практически не влияет на прочность физико-химических связей, образующихся между смолой СФ-342А и полипропиленовой нитью.
Ответ:
|Qдоп
 |=56 кДж/моль; |Qдоп
|=56 кДж/моль; |Qдоп
 |=54 кДж/моль.
|=54 кДж/моль.
42. Используя соотношение γ=А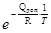 (1), аналогичное соотношению Вант-Гоффа для константы равновесия K
:
K
=
A (1), аналогичное соотношению Вант-Гоффа для константы равновесия K
:
K
=
A
 (2), где А-предэкспоненциальный множитель; Qдоп
- тепловой эффект взаимодействия между связующим и наполнителем; Q- тепловой эффект рассматриваемого обратимого процесса, найти массовую долю γ2
переходного слоя в системе анилино-фенолоформальдегидная смола СФ-342А – полипропиленовая нить ППН при температуре Т2
=443 К, если при Т1
=393 К известно значение γ1
=0,38. Тепловой эффект Qдоп
взаимодействия ППН со связующим в данном случае составляет Qдоп
=-45 кДж/моль. Рекомендуется записать соотношение (1) в логарифмической форме для температуры Т1
и для температуры Т2
.
(2), где А-предэкспоненциальный множитель; Qдоп
- тепловой эффект взаимодействия между связующим и наполнителем; Q- тепловой эффект рассматриваемого обратимого процесса, найти массовую долю γ2
переходного слоя в системе анилино-фенолоформальдегидная смола СФ-342А – полипропиленовая нить ППН при температуре Т2
=443 К, если при Т1
=393 К известно значение γ1
=0,38. Тепловой эффект Qдоп
взаимодействия ППН со связующим в данном случае составляет Qдоп
=-45 кДж/моль. Рекомендуется записать соотношение (1) в логарифмической форме для температуры Т1
и для температуры Т2
.
Решение:
Записываем соотношение (1) для температур Т1
и Т2
:
γ1 =
A (2) (2)
γ2
=A (3) (3)
Почленно логарифмируем соотношения (2) и (3):
 (4) (4)
 (5), (5),
из соотношения (4) вычитаем соотношение (5):
 , ,
откуда  . Подставив сюда значения всех величин из условия задачи, получаем: . Подставив сюда значения всех величин из условия задачи, получаем:
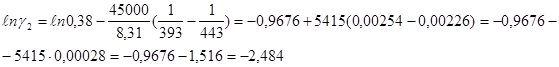
 10-1,08
=10-2
∙100,92
=8,3∙10-2
=0,083. 10-1,08
=10-2
∙100,92
=8,3∙10-2
=0,083.
Результат показал, что при повышении температуры отверждения массовая доля переходного слоя уменьшается, так как взаимодействие между наполнителем и связующим – экзотермический процесс.
Ответ:
 . .
43. Равновесная деформация жгута из диацетатных нитей при усилии Р=0,7 Н составила Δ =2,34 мм (однонаправленное растяжение). Начальная длина жгута между зажимами =2,34 мм (однонаправленное растяжение). Начальная длина жгута между зажимами  =140,0 мм, текс жгута t=554 (то есть =140,0 мм, текс жгута t=554 (то есть
1000 м такого жгута имеют массу 554г.).Испытания проводились при Т=413 К. Плотность диацетата целлюлозы ρ=1320 кг/м3
.
Вычислить относительную деформацию ε , площадь поперечного сечения S, мкм2
по соотношению S=1000t/ρ (1), где ρ выражено в г/см3
.
Далее определить напряжение в жгуте σ= (2), модуль упругости (2), модуль упругости
ЕР
= (3) и среднюю массу молекулярных цепей между узлами сетки (3) и среднюю массу молекулярных цепей между узлами сетки
MC
= (4), где ρ- плотность, кг/м3
; R- универсальная газовая постоянная R=8,31 Дж/моль∙К. В каких единицах выражается напряжение σ и модуль упругости Е в системе СИ? (4), где ρ- плотность, кг/м3
; R- универсальная газовая постоянная R=8,31 Дж/моль∙К. В каких единицах выражается напряжение σ и модуль упругости Е в системе СИ?
Решение:
1. Расчет относительной деформации ε:
ε =
2. Вычисляем площадь поперечного сечения исходной нити :
S=
При расчете по данному соотношению величину S выражают в мкм2
(эта размерность определяемая коэффициентом 103
при выражении ρ в г/см3
)
3.Механическое напряжение σ относительно начального сечения вычисляем по соотношению:
σ = =1,7∙106
Па=1,7 МПа =1,7∙106
Па=1,7 МПа
4.Для упругих деформаций модель упругости Ep
при растяжении рассчитывается как Ер
= =1,7∙106
Па/0,017=108
Па =1,7∙106
Па/0,017=108
Па
5. Известно, что модуль упругости сетчатого полимера при сдвиге Ec
дв
=nc
RT= , а также Ер
=3Есдв
. , а также Ер
=3Есдв
.
Отсюда следует: Mc
=
Полученное значение Mc
сравнительно невелико.Это есть средняя масса цепей между химическими и физическими узлами сетки.
Ответ:
ε=0,017; S=4,2∙10-7 м2
; σ=1,7∙106
Па;
E=108
Па; Mc
=140 г/моль
Ответы:
1. m=65,4 г/мин, r= 160 мкм
2. q=2,75∙10-2
; вязкость уменьшилась в 36 раз
3. m=0,95
4. σ=0,07 Па
5. Mc
=0,012 кг/моль=12 г/моль
6. d=0,07 мкм
7. V=2,09 см3
/см3
8. τ=43 с
9. δ=0,03∙10-4
см=0,03 мкм
10. S=56 м2
; Sуд
=12 м2
/г
11. 1.Q373
=-122-15=-137 кДЖ/моль
2.Q373
=-122-17=-139 кДж/моль
Литература
:
1. Липатов Ю.С.
|