Вариант 1
Задание 1
Дан треугольник АВС: А(5;4), В(2;0), С(8;3). Найти:
1) длину стороны АВ;
2) внутренний угол А с точностью до градуса;
3) уравнение и длину высоты, опущенной из вершины С;
4) точку пересечения высот;
5) уравнение медианы, проведенной из вершины С;
6) систему линейных неравенств, определяющих треугольник АВС.
Сделать чертеж.

Решение:
1) Найдем координаты вектора  : :
 . .
Длина стороны АВ равна
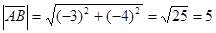 . .
2) Внутренний угол А будем искать как угол между векторами  и и  : :
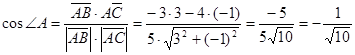 . .
Тогда угол 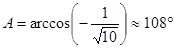 . .
3) Прямая 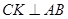 проходит через точку С(8;3) и имеет нормалью вектор проходит через точку С(8;3) и имеет нормалью вектор 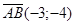 . .
По формуле 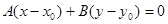 получим уравнение высоты: получим уравнение высоты:
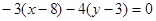 , ,  , ,
 - уравнение СК. - уравнение СК.
Длину высоты 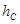 будем искать как расстояние от точки С до прямой АВ. Эта прямая проходит через точку А и имеет направляющий вектор будем искать как расстояние от точки С до прямой АВ. Эта прямая проходит через точку А и имеет направляющий вектор 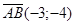 . По формуле . По формуле  получим получим
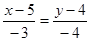 , , 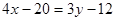 , ,
 - уравнение прямой АВ. - уравнение прямой АВ.
Воспользуемся формулой 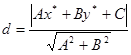 . .
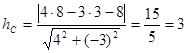 . .
4) Известно, что высоты треугольника пересекаются в одной точке Р. Уравнение высоты СК найдено. выведем аналогичным способом уравнение высоты ВН, проходящей через точку В перпендикулярно вектору  . .
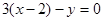 , , 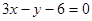 . .
Координаты точки Р найдем как решение системы:
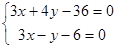 , ,  , , 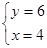 . .
Р(4;6).
5) Координаты основания медианы будут:
6)
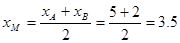 , ,  , ,
М(3.5;2).
Уравнение медианы найдем, используя формулу 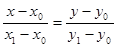 , как уравнение прямой, проходящей через две точки: С и М. , как уравнение прямой, проходящей через две точки: С и М.
 , , 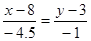 , ,  , ,
 - уравнение медианы СМ. - уравнение медианы СМ.
7) Треугольник АВС задается пересечением трех полуплоскостей, определяемых через уравнения прямых АВ, ВС, АС.
Найдем уравнения ВС и АС по формуле 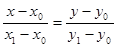 . .
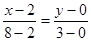 , , 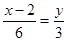 , , 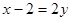 , ,
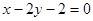 - уравнение ВС. - уравнение ВС.
 , , 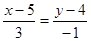 , , 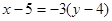 , ,
 - уравнение АС. - уравнение АС.
 - уравнение АВ. - уравнение АВ.
Чтобы определить полуплоскость, в которой лежит треугольник АВС относительно прямой АВ, подставим координаты точки С в уравнение АВ:
4∙8-3∙3-8=32-9-8=15≥0.
Тогда полуплоскость, в которой лежит треугольник АВС относительно прямой АВ, определяется неравенством: 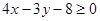 . .
Аналогично для прямых ВС и АС.
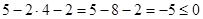 ; ; 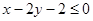 . .
 ; ; 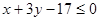 . .
Таким образом, треугольник АВС определяется системой неравенств:
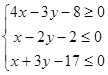 . .
Ответ003A
1) 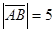 ; ;
2) 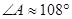 ; ;
3)  ; ;  ; ;
4) Р(4;6);
5)  ; ;
6) 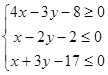 . .
Задание 2
Даны векторы 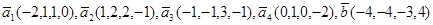 . Доказать, что векторы . Доказать, что векторы  образуют базис четырехмерного пространства, и найти координаты вектора образуют базис четырехмерного пространства, и найти координаты вектора 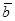 в этом базисе. в этом базисе.
Решение:
 - система из четырех четырехмерных векторов. Следовательно, чтобы доказать, что она является базисом пространства - система из четырех четырехмерных векторов. Следовательно, чтобы доказать, что она является базисом пространства  , достаточно доказать ее линейную независимость. , достаточно доказать ее линейную независимость.
Составим и вычислим определитель матрицы, столбцами которой являются векторы  : :
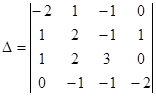 . .
Для вычисления этого определителя, разложим его по четвертому столбцу:
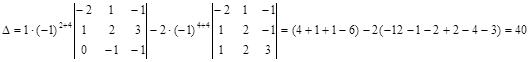 . .
Определитель Δ≠0, следовательно  - линейно независимая система из четырех четырехмерных векторов, то есть базис пространства - линейно независимая система из четырех четырехмерных векторов, то есть базис пространства  . .
Для нахождения координат вектора 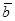 в этом базисе, разложим вектор в этом базисе, разложим вектор 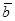 по базису по базису  : :
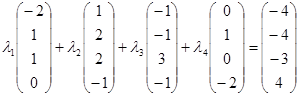 .3 .3
Найдем  - координаты вектора - координаты вектора 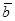 в этом базисе. в этом базисе.
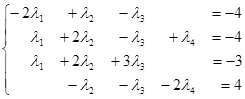 . .
Решим эту систему методом Гаусса.
Поменяем местами первое и третье уравнение:

Первое уравнение, умноженное последовательно на (-1) и (2), прибавим соответственно ко второму и третьему уравнениям системы:
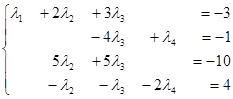
Поменяем местами второе и четвертое уравнения, третье разделим на 5:

Прибавим к третьему уравнению второе:
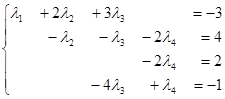
Поменяв местами третье и четвертое уравнение, получим систему треугольного вида:

Система имеет единственное решение. Решаем снизу вверх:
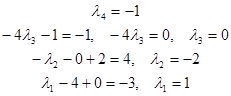
Вектор 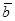 в базисе в базисе  имеет координаты имеет координаты  . .
Задание 3
Найти производные функций:
а) 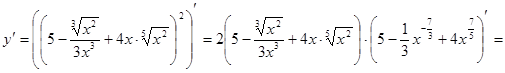

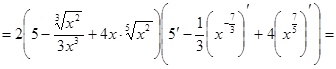 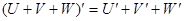 и и
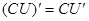
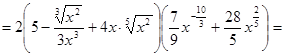 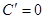
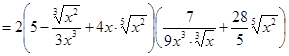 . .
б) 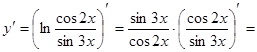 
 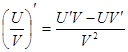
  и и 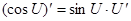
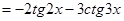 . .
в)  
 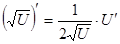
 . .
г) 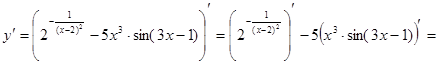
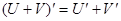

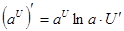
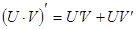
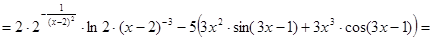  , ,
 . . 
Задание 4

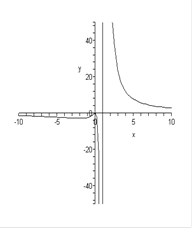
1. Область определения  . .
2. На концах области определения:  . .
 - значит - значит 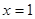 - вертикальная асимптота. - вертикальная асимптота.
Найдем наклонные асимптоты, если они есть:


У функции есть горизонтальная асимптота  . .
3. Так как область определения не симметрична относительно 0, функция не является ни четной, ни нечетной, т. е. функция общего вида.
4. Функция периодичностью не обладает.
5. Найдем первую производную функции:
 . .
Решая уравнение  , получим две критические точки , получим две критические точки  , еще одна критическая точка , еще одна критическая точка  . .
Результаты исследования на монотонность и экстремум оформим в виде таблицы:
| x |
(-∞;-2) |
-2 |
(-2;0) |
0 |
(0;1) |
1 |
(1;+∞) |
| y’ |
- |
0 |
+ |
0 |
- |
Не существует |
- |
| y |
Убывает |
-80/27
min
|
Возрастает |
0
max
|
Убывает |
Не существует |
Убывает |
6. Находим вторую производную функции:
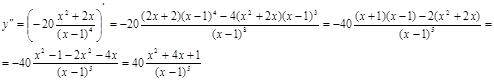
Решая уравнение  , получим , получим  , , 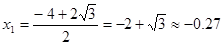
 - это критические точки. Еще одна критическая точка - это критические точки. Еще одна критическая точка  . .
Результаты исследования на выпуклость и точки перегиба оформим в виде таблицы:
7. Учитывая результат пункта 2 и непрерывность функции при 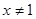 , значения функции заполняют промежуток (-∞;+∞). , значения функции заполняют промежуток (-∞;+∞).
8. Пересечение с осью Ох:  , , 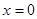 , точка (0;0). Она же – точка пересечения с Оу. , точка (0;0). Она же – точка пересечения с Оу.
9. Необходимости в дополнительных точках нет.
Задание 5
Применяя таблицу интегралов и метод замены переменных, найти неопределенные интегралы. Результаты проверить дифференцированием.
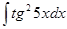
Произведем замену переменной: 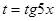 , тогда , тогда
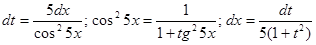

Проверка:


Произведем замену переменной: 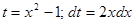 , тогда , тогда
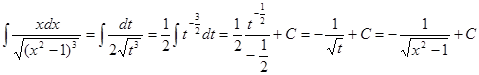
Проверка:
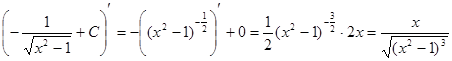
Применяя метод интегрирования по частям, найти неопределенные интегралы. Результаты проверить дифференцированием.
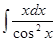
Возьмем 
Применяя формулу интегрирования по частям:  , получим: , получим:
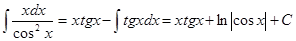
Проверка:

Применяя метод интегрирования рациональных алгебраических функций, найти неопределенные интегралы. Результаты проверить дифференцированием.
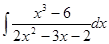
Подынтегральное выражение представляет собой неправильную дробь. Выделим целую часть, деля числитель на знаменатель.

Следовательно: 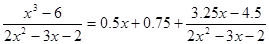
Разложим многочлен 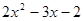 . .
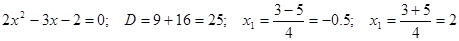 , тогда , тогда
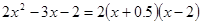
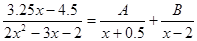 . .
Умножим обе части этого тождества на 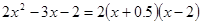 , получим , получим
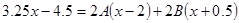
 , тогда , тогда
 . Решая эту систему, получим А=1.225; В=0.4. . Решая эту систему, получим А=1.225; В=0.4.
Таким образом:

Проверка:

Ответ: 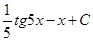 ; ; 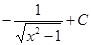 ; ;  ; ;
 . .
Задание 6
Вычислить площадь фигуры, ограниченной графиками функций 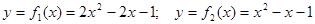
Находим координаты точек пересечения двух парабол, решая систему уравнений:
 . Приравнивая правые части, получим квадратное уравнение: . Приравнивая правые части, получим квадратное уравнение:
 . Его решения . Его решения 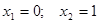 . Тогда координаты точек пересечения А(0;-1), В(1;-1). . Тогда координаты точек пересечения А(0;-1), В(1;-1).
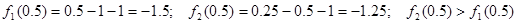 , поэтому , поэтому
 кв. ед. кв. ед.
Вычислить площадь фигуры, ограниченной графиками функций 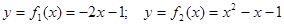
Находим координаты точек пересечения прямой и параболы, решая систему уравнений:
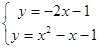 . Приравнивая правые части, получим квадратное уравнение: . Приравнивая правые части, получим квадратное уравнение:
 . Его решения . Его решения 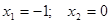 . Тогда координаты точек пересечения А(-1;1), В(0;-1). . Тогда координаты точек пересечения А(-1;1), В(0;-1).
 , поэтому , поэтому
 кв. ед. кв. ед.
|