Содержание
Введение
Дефекты реальных кристаллов
Принцип работы биполярных транзисторов
Поверхностные явления в полупроводниках
Задача 1
Задача 2
Задача 3
Литература
В настоящее время невозможно найти какую-либо oтрасль промышленности, в которой не использовались бы электронные приборы или электронные устройства измерительной техники, автоматики и вычислительной техники. Причем тенденция развития такова, что доля электронных информационных устройств и устройств автоматики непрерывно увеличивается. Поэтому современный специалист в области электроники должен знать основные физические принципы и законы, составляющие теоретический фундамент функционирования приборов, устройств и систем, т.е. той техники, творцом которой он призван быть.
Цель контрольной работы - рассмотреть теоретические вопросы, в основном связанные с физическими принципами функционирования электронных приборов и рассмотреть практическое применение теоретических вопросов.
Реальные кристаллы всегда имеют всевозможные дефекты, нарушающие строгую периодичность их структуры и оказывающие сильное влияние практически на все их свойства - электрические, механические, оптические и др. Рассмотрим кратко наиболее важные дефекты кристаллов.
Примеси. Твердые тела сколь угодно высокой степени чистоты всегда содержат примеси. В зависимости от их природы и количества они могут находиться в кристалле или в растворенном состоянии, или в виде более или менее крупных включений. Процесс растворения состоит в том, что примесные атомы внедряются в промежутки между атомами кристалла (рис.1.1, а)
или замещают часть этих атомов, размещаясь в узлах решетки (рис.1.1, б).
В первом случае твердый раствор называется раствором внедрения, во втором - раствором замещения. Так как чужеродные атомы по своей физической природе и размерам отличаются от атомов основного кристалла, то их присутствие вызывает искажение решетки.

Рис.1.1 Искажение кристаллической решетки в твердых растворах внедрения (а) и замещения (б)
Дефекты по Френкелю и по Шоттки. Распределение энергии между атомами твердого тела, как и между молекулами газа и жидкости, является неравномерным. При любой температуре в кристалле имеются атомы, энергия которых во много раз больше или меньше среднего значения, определяемого температурой кристалла. Атомы, обладающие в данный момент достаточно высокой энергией, могут не только удаляться на значительные расстояния от положений равновесия, но и преодолевать потенциальный барьер, созданный соседними атомами, и переходить в новое окружение, в новую ячейку. Такие атомы приобретают способность как бы "испаряться" из своих узлов и "конденсироваться" в междоузлиях (рис.1.2, а). Этот процесс сопровождается возникновением вакантного узла (вакансии) и атома в междоузлии (дислоцированного атома). Такого рода дефекты решетки называются дефектами по Френкелю.
Помимо внутреннего испарения, возможно полное или частичное испарение атомов с поверхности кристалла. При полном испарении атом покидает поверхность кристалла и переходит в пар, при частичном испарении он с поверхности переходит в положение над поверхностью (рис.1.2, б). В обоих случаях в поверхностном слое кристалла образуется вакансия. Путем замещения глубже лежащим атомом вакансия втягивается внутрь кристалла. Такое образование вакансий не сопровождается одновременным внедрением атомов в междоузлия, т.е. появлением дислоцированных атомов. Такого рода вакансии называют дефектами по Шоттки. Их источником могут быть и всевозможные несовершенства кристалла: недостроенные атомные плоскости, границы блоков и зерен, микроскопические трещины и др.

Рис.1.2 Дефекты по Френкелю (а)
и по Шоттки (б)
Равновесная концентрация дефектов в кристалле зависит прежде всего от температуры, так как с ростом температуры увеличивается число атомов, энергия которых оказывается достаточной для преодоления связи с соседями и образования дефекта. В соответствии с законом Больцмана число таких атомов прямо пропорционально ехр ( - U/
kT),
где U -
энергия образования дефекта;
Т -
абсолютная температура кристалла.
Для дефектов по Френкелю число их в кристалле, содержащем N
узлов, равно
Nф
=
ANехр (-
Uф
/
kT), (
1.1)
для дефектов по Шоттки
NШ
=
Nexp (-
Uui
/
kT), (
1.2)
где Uф
, Uш
-
энергия образования дефектов по Френкелю и Шоттки; соответственно;
А -
число одинаковых междоузлий, приходящееся на один атом решетки.
При образовании дефектов по Френкелю атому, переходящему из узла в междоузлие, необходимо не только разрывать связи с соседними атомами, но и раздвигать их, внедряясь между ними. Это требует затраты значительной энергии и может происходить практически лишь в кристаллах, состоящих из атомов двух сортов, сильно различающихся своими размерами, например в ионных кристаллах NaCl, AgCl, NaBr и др. (ионный радиус Na+ равен 0,095 нм, Ag+ 0,11 нм; ионный же радиус Br -
равен 0, 195 нм, С1 -
0,181 нм), а также в твердых растворах внедрения, например в сталях (rF
е
= 0,126нм, rс
=
0,077 нм). В кристаллах же с плотной упаковкой однотипных атомов, например в металлических, дефекты по Френкелю возникать практически не могут и основными являются дефекты по Шоттки. Расчет показывает, что в кристалле меди при Т =
1000° С
концентрация вакансий Nm
/
N≈
10-4
, концентрация дефектов по Френкелю Nф
/
N≈
10-39
.
Для рассмотрения принципа работы биполярного транзистора воспользуемся схемой, приведенной на рис.2.1 Из рисунка видно, что транзистор представляет собой по существу два полупроводниковых диода, имеющих одну общую область - базу, причем к эмиттерному р-п
переходу приложено напряжение Е1
в прямом (пропускном) направлении, а к коллекторному переходу приложено напряжение Е2
в обратном направлении. Обычно |Е2
| " |Е1
|. При замыкании выключателей SA1
и SA2
через эмиттерный р-п
переход осуществляется инжекция дырок из эмиттера в область базы. Одновременно электроны базы будут проходить в область эмиттера. Следовательно, через эмиттерный переход пойдет ток по следующему пути: + Е1, м
иллиамперметр РА1,
эмиттер, база, миллиамперметр РА2,
выключатели SA2
и SA1,
- E1
.
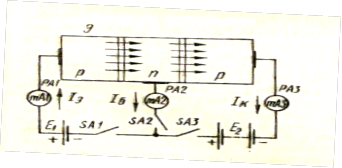
Рис.2.1 К пояснению принципа работы транзистора
Если выключатель SA1
разомкнуть, а выключатели SA2
и SA3
замкнуть, то в коллекторной цепи пройдет незначительный обратный ток, вызываемый направленным движением не основных носителей заряда - дырок базы и электронов коллектора. Путь тока: +Е2
,
выключатели SA3
и SA2,
миллиамперметр РА2,
база, коллектор, миллиамперметр РАЗ, - Е2
.
Таким образом, каждый из р-п
переходов в отдельности подчиняется тем закономерностям, которые были установлены ранее.
Рассмотрим теперь прохождение токов в цепях транзистора при замыкании всех трех ключей. Как видно из рис.2.2, подключение транзистора к внешним источникам питания приводит к изменению высоты потенциальных барьеров р-п
переходов. Потенциальный барьер эмиттерного перехода понижается, а коллекторного - увеличивается.
  
  
Рис.2.2 Энергетическая диаграмма включенного транзистора
Ток, проходящий через эмиттерный переход, получил название эмиттерного тока (Iэ
). Этот ток равен сумме дырочной и электронной составляющих
Iэ =
IэР
+
Iэ
n
. (2.1)
Если бы концентрация дырок и электронов в базе и эмиттере была одинаковой, то прямой ток через эмиттерный переход создавался бы перемещением одинакового числа дырок и электронов в противоположных направлениях. Но в транзисторах, как было сказано выше, концентрация носителей заряда в базе значительно меньше, чем в эмиттере. Это приводит к тому, что число дырок, инжектированных из эмиттера в базу, во много раз превышает число электронов, движущихся в противоположном направлении. Следовательно, почти весь ток через эмиттерный р-п
переход обусловлен дырками. Эффективность эмиттера оценивается коэффициентом инжекции γ,который для транзисторов типа р-п-р
равен отношению дырочной составляющей эмиттерного тока к общему току эмиттера:
γ =
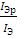 = =
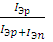 = =
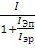 (
7.2) (
7.2)
В современных транзисторах коэффициент γ обычно мало отличается от единицы (γ ≈ 0,999).
Инжектированные через эмиттерный переход дырки проникают вглубь базы. В зависимости от механизма прохождения носителей заряда в области базы отличают бездрейфовыеи дрейфовые транзисторы.
В бездрейфовых транзисторах перенос неосновных носителей заряда через базовую область осуществляется в основном за счет диффузии. Такие транзисторы обычно получают описанным выше методом сплавления. В дрейфовых транзисторах в области базы путем соответствующего распределения примесей создается внутреннее электрическое поле и перенос неосновных носителей заряда через базу осуществляется в основном за счет дрейфа. Такие транзисторы, как уже отмечалось, обычно получают методом диффузии примесей.
Несмотря на определенные различия в механизме прохождения носителей заряда через базу, и в бездрейфовых, и в дрейфовых транзисторах дырки, попав в базу, для которой они являются неосновными носителями заряда, начинают рекомбинировать с электронами. Но рекомбинация - процесс не мгновенный. Поэтому почти все дырки успевают пройти через тонкий слой базы и достигнуть коллекторного р-п
перехода прежде, чем произойдет рекомбинация. Подойдя к коллектору, дырки начинают испытывать действие электрического поля коллекторного перехода. Это поле для дырок является ускоряющим, поэтому они в результате экстракции быстро втягиваются из базы в коллектор и участвуют в создании тока коллектора.
Цепь коллекторного тока: +Е2
,
выключатели SA3
и SA1,
миллиамперметр РА1,
эмиттер, база, коллектор, миллиамперметр РАЗ,-Е2
(
рис.2.1).
Принимая во внимание малую степень рекомбинации дырок с электронами в области базы, можно считать ток коллектора Iк
примерно равным току эмиттера Iэ:
Iк
≈
Iэ
. (2.3)
Те дырки, которые все же рекомбинируют в области базы с электронами, участвуют в создании тока базыIб
, проходящего в цепи: +Е1
,
миллиамперметр РА1,
эмиттер, база, миллиамперметр РА2,
выключатели SA2
и SA1.
Следовательно, ток базы равен разности токов эмиттера и коллектора
Iб
=
I -
Iк
. (2.4)
Нетрудно заметить также, что ток эмиттера, измеряемый миллиамперметром РА1,
равен сумме токов базы и коллектора, измеряемых соответственно приборами РА2
и РАЗ,
т.е.
Iэ =
IБ
+
Iк
. (
2.5)
Необходимо обратить внимание на то, что, хотя электроны и дырки движутся в противоположных направлениях, токи в цепях транзистора проходят в одном направлении,
совпадающем с направлением движения носителей заряда положительной полярности - дырок. Это нетрудно понять, если учесть, что противоположное направление движения электронов и дырок компенсируется их противоположным знаком. Следовательно, при образовании тока в цепях транзистора речь может идти не о разности, а именно о сумме электронной и дырочной составляющих.
Для оценки влияния рекомбинации носителей заряда в базе на усилительные свойства транзистора используется коэффициент переноса носителей в базе,который показывает, какая часть инжектированных эмиттером дырок достигает коллекторного перехода. Этот коэффициент можно определить по формуле
δ=
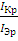 ; (
2.6) ; (
2.6)
Коэффициент переноса δ тем ближе к единице, чем меньше толщина базы и концентрация электронов в базе по сравнению с концентрацией дырок в эмиттере.
Одним из основных параметров транзистора является коэффициент передачи тока эмиттера,который равен отношению приращения тока коллектора к приращению тока эмиттера при неизменном напряжении на коллекторном переходе:
α = 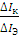 (2.7) (2.7)
Этот коэффициент может быть выражен через величины γ
и δ следующим соотношением:
α
= γδ. (
2.8)
Так как γ и δ меньше единицы, то коэффициент передачи тока эмиттера α
также не превышает единицы. Обычно а
= 0,95...0,99. Чем больше коэффициент а,
тем меньше отличаются между собой токи коллектора и эмиттера, тем более эффективно могут быть использованы усилительные свойства транзистора.
Поскольку в цепи коллектора кроме тока, обусловленного экстракцией дырок из базы в коллектор, протекает собственно обратный ток коллекторного перехода Iкбо
, то полный ток коллектора
Iк = α
Iэ
+
Iкбо
(2.9)
Учитывая, что ток Iкбо
по величине незначителен, можно принять
Iк = α
Iэ
(2.10)
Из выражения (2.10) следует, что транзистор представляет собой управляемый прибор, так как величина его коллекторного тока зависит от величины тока эмиттера.
В зависимости от полярности напряжений, приложенных к эмиттерному и коллекторному переходам транзистора, различают четыре режима его работы:
Активный режим. На эмиттерный переход подано прямое напряжение, а на коллекторный - обратное. Этот режим является основным режимом работы транзистора. Вследствие того, что напряжение в цепи коллектора значительно превышает напряжение, подведенное к эмиттерному переходу, а токи в цепях эмиттера и коллектора практически равны, следует ожидать, что мощность полезного сигнала на выходе схемы (в коллекторной цепи) может оказаться намного больше, чем во входной (эмиттерной) цепи транзистора.
Режим отсечки. К обоим переходам подводятся обратные напряжения. Поэтому через них проходит лишь незначительный ток, обусловленный движением неосновных носителей заряда. Практически транзистор в режиме отсечки оказывается запертым.
Режим насыщения. Оба перехода находятся под прямым напряжением. Ток в выходной цепи транзистора максимален и практически не регулируется током входной цепи. В этом режиме транзистор полностью открыт.
Инверсный режим. К эмиттерному переходу подводится обратное напряжение, а к коллекторному - прямое. Эмиттер и коллектор меняются своими ролями - эмиттер выполняет функции коллектора, а коллектор - функции эмиттера. Этот режим, как правило, не соответствует нормальным условиям эксплуатации транзистора.
Энергетический спектр электрона, движущегося в строго периодическом поле неограниченного кристалла, имеет зонную структуру: полосы разрешенных энергий отделены друг от друга зонами запрещенных энергий. Нарушение периодичности потенциала, вызванное дефектами решетки (примесными атомами, вакансиями и др.), приводит к возникновению в запрещенной зоне дискретных уровней.
Подобными дефектами являются и свободные поверхности кристалла, на которых происходит обрыв решетки и нарушение периодичности ее потенциала (рис.3.1, а). Влияние такого рода дефектов на энергетический спектр электронов было исследовано Таммом в 1932 г. Он показал, что обрыв решетки приводит к появлению в запрещенной зоне полупроводника разрешенных дискретных уровней энергии для электронов, расположенных в непосредственной близости от поверхности кристалла (рис.3.2, б). Такие уровни получили название поверхностных уровней или поверхностных состояний.

Рис.3.1 Возникновение поверхностных состоянии: а - обрыв периодического потенциала решетки у поверхности кристалла; б - поверхностные состояния, возникающие вследствие обрыва решетки; в - чужеродные атомы М на поверхности; г - типы поверхностных состояний (Ед
-донорные, Еа
- акцепторные, Ер
- рекомбинационные)
Наглядное представление о возникновении поверхностных состояний можно получить из рассмотрения связей, действующих между атомами в объеме и на поверхности кристалла. На рис.3.2 изображена плоская модель решетки германия. Атом в объеме кристалла окружен четырьмя ближайшими соседями, связь с которыми осуществляется путем попарного обобществления валентных электронов. У атомов, расположенных на свободной поверхности АА
, одна валентная связь оказывается разорванной, а электронная пара неукомплектованной. Стремясь укомплектовать эту пару и заполнить свою внешнюю оболочку до устойчивой восьмиэлектрон-ной конфигурации, поверхностные атомы ведут себя как типичные акцепторы, которым в запрещенной зоне соответствуют акцепторные уровни Еа
(рис.3.1, б). Электроны, попавшие на эти уровни из валентной зоны, не проникают в глубь кристалла и локализуются на расстоянии порядка постоянной решетки от поверхности. В валентной зоне возникают при этом дырки, а в поверхностном слое полупроводника - дырочная проводимость.
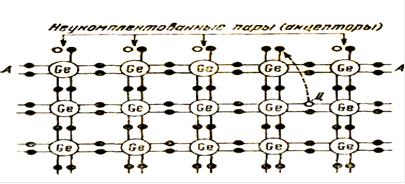
Рис.3.2 Схема возникновения акцепторных поверхностных состояний на чистой поверхности полупроводника
Рассмотренные поверхностные состояния возникают на идеально чистой бездефектной поверхности, получить которую практически невозможно. В реальных условиях поверхностные свойства полупроводников определяются поверхностными состояниями, созданными главным образом чужеродными атомами (молекулами). на поверхности. На рис.3.1, в
показана зонная структура полупроводника. Вертикальной прямой ВС
обозначена одна из свободных его поверхностей. Предположим, что на этой поверхности химически сорбировалась частица М.
При такой сорбции волновые функции решетки и частицы перекрываются настолько, что частицу можно рассматривать как примесь, локально нарушающую периодичность потенциала решетки и приводящую к возникновению в запрещенной зоне поверхностного уровня.
Характер таких уровней зависит от природы поверхности и частиц. Они могут быть акцепторными, донорными и рекомбинационными (рис.3.1, г).
Так, кислород, сорбированный на поверхности германия, создает акцепторные уровни, вода - донорные. Если уровни Р
являются акцепторными, то они захватывают электроны и заряжают поверхность полупроводника отрицательно с поверхностной плотностью σ -
= gN
f - ф-д
, где N -
число молекул, адсорбированных единицей поверхности кристалла; fф_д
- функция Ферми - Дирака, выражающая вероятность заполнения поверхностных уровней электронами; q -
заряд электрона. Если уровни Р
являются донорными, то они, отдавая электроны кристаллу, заряжают поверхность полупроводника положительно с плотностью σ+
= qNf
ф-д
;
где f
ф_д
- вероятность того, что поверхностные уровни являются пустыми, т.е. частицы М
ионизированы.
При высокой плотности поверхностных состояний они, взаимодействуя друг с другом, могут размыться в поверхностную зону. Электроны в этой зоне могут двигаться только вдоль поверхности.
Быстрые и медленные поверхностные состояния. Поверхностные состояния, обусловленные дефектами поверхности и адсорбцией на ней чужеродных частиц, располагаются в непосредственной близости от поверхности и находятся в хорошем контакте с объемом полупроводника. Поэтому время установления равновесия этим состояний с объемом полупроводника (время перехода электронов из энергетических зон на поверхностные уровни или обратно) оказывается очень небольшим (≈10-7
с). Такие состояния называют - быстрымиповерхностными состояниями. Они имеют плотность порядка 1015
м-2
, зависящую от характера обработки поверхности, и могут обладать большими сечениями захвата как для электронов, так и для дырок, вследствие чего могут служить эффективными центрами рекомбинации.
В нормальных условиях поверхность полупроводника покрыта слоем окисла толщиной по крайней мере в десятки ангестрем (рис.3.3, а).
На внешней поверхности окисла сорбируются примесные атомы, создающие внешние или медленные поверхностные состояния (рис.3.3, б).
Время установления равновесия таких состояний с объемом полупроводника значительно больше, чем для быстрых состояний, и колеблется от микросекунд до минут, часов и даже суток. Это обусловлено тем, что вероятность прохождения электронов сквозь окисный слой, являющийся изолятором, весьма низка. С увеличением толщины окисной пленки постоянная времени увеличивается.
Медленные поверхностные состояния могут создаваться также атомами примеси, находящимися в самом окисле. Плотность медленных состояний значительно больше, чем быстрых (1017
- 1019
м-2
), и сильно зависит от их природы и состояния внешней среды.

Рис.3.3 Структура поверхностного слоя германия (а)
и расположение быстрых и медленных поверхностных состояний (изгиб зон у поверхности не показан) (б): 1
- германий; 2 -
переходный слой; 3
- окисный слой; 4 -
адсорбированные примеси.
Вычислить для температуры 300°С контактную разность потенциалов р-п перехода, сформированного в кремнии, если равновесные концентрации основных носителей заряда в р-n-областях одинаковы и равны 10 17
см-3
, а собственная концентрация ni
= 1013
см-3
.
Решение:
Vk
= (
KT/
e)
ln (
nn
/
n
p
)
Учитывая, что
nn
·
pp
=
ni
2
Vk
= (
KT/
e)
ln (
nn
·
pp
/
ni
2
)
Величину ni
определяем по формуле
ni
=
2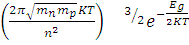
Значения nn
и pp
определим, исходя из выражений для удельной проводимости:
σ
n-Si
= σnn
+ σpn
= e (nn
Un
+ pn
Up
) =e
[nn
Un
+
(ni
2
/nn
) Up
]
σ
p
-
Si
=
σpp
+
σpp
=
e
(
np
Up
+
pp
Un
) =
e
[np
Up
+
(ni
2
/pp
) Un
]
Отсюда
nn
= σ
n-Si
/2e
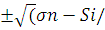 2
e) 2
- ni
2
Un
Up 2
e) 2
- ni
2
Un
Up
pp
= σ
p-Si
/2e
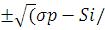 2
e) 2
- ni
2
Un
Up 2
e) 2
- ni
2
Un
Up
Подставляя численные значения, получим:
ni
2
=
0,98 ·1018
м - 3
;
nn
= 0,87 ·1023
м - 1
;
pp
= 0,87 ·1021
м - 1
;
Vk
= 0,395 В
.
Определить положение узла, направления, плоскости в кристалле Si, индексы Миллера которых [[1 0 1]], [1/2 1 1], (121).
Найти температуру истощения примеси Sin-типа, если красная граница фотопроводимости составляет 6·10-6
м. Постоянная Холла при этой температуре 4·10-3
м-3
/К. Рассеяние носителей заряда осуществляется на ионизированных примесях, mn
=0,7m0
.
Положение любого узла решетки определяется заданием трех координат: х, у,
z.
Эти координаты можно выразить следующим образом: х=та,
y=
nb,
z=
pc
где а,
Ь, с - параметры решетки: т, п. р -
целые числа. За единицу измерения длины обычно принимают параметры решетки. Тогда координаты узла будут просто числа т, п,р
Это и есть индексы Миллера узла. Учитывая вышесказанное, узел I имеет индексы 1 - [[1 0 1]], а узел 2- [1 1 0].
За направление в кристаллической решетке принимают прямую, проходящую через начало координат. Тогда индексы узла I кристаллической решетки, через который она проходит, однозначно определяют индексы направления. Поэтому направление I имеет индексы [0 1 1], а направление 2 -
[1 1 0].
Индексы плоскости отыскивают следующим образом. Выражают отрезки A, В, С, которые плоскость отсекает на осях решетки, в осевых единицах. Находят величины, обратные этим отрезкам: 1/
A
, 1/В, 1/С.
Полученные дроби приводят к общему знаменателю. Пусть таковым будет число D.
Тогда числа h=
D/
A,
K=
D/
B,
l =
D/
C
принимают за индексы плоскости. Плоскость, изображенная на рис.5.1, отсекает по соответствующим осям отрезки А
= 1, В=1/2, С
=1
. Тогда 1/А
=1; 1/В =
2; 1/С
=1, D
=1; h=
1; К
= 2; l = 1.

Рис.5.1
Область истощения примеси. По мере повышения температуры концентрация электронов на примесных уровнях уменьшается - примесные уровни истощаются. При полном истощении этих уровней концентрация электронов в зоне проводимости будет равна концентрации примеси, если концентрацией собственных носителей можно по-прежнему пренебречь:
n =
Nn
(5.1)
Воспользовавшись для п
выражением
n = N
e
exp
(
μ
/kT) (
5.2), получим N
e
exp
(
μ
/kT)
= N
д
. (5.3).
Отсюда находим
μ =
kTln (
N
д
/
Nc
). (
5.4)
Уровень μ должен располагаться ниже уровней - Е
д
так как при μ = - Е
д
ионизации подвергается в среднем лишь половина примесных уровней. Однако обычно за температуру истощения примесей принимают температуру Та
,
при которой уровень Ферми совпадает с донорными уровнями Е
д
: μ
s
= - Е
д
.
Положив в формуле (5.2) Т
= Т
s
,
μ = μs
и п
= N
д
/2,
получим
μs
=
kTs
ln
(
N
д
/2
Nc
) = - Ед
(
5.5)
Отсюда находим температуру истощения примесей
Ts
=
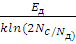 (
5.6) (
5.6)
Определить, какие электрохимические процессы будут происходить на аноде и катоде. Найти толщину осажденной на катоде металлической пленки. Электролитом является водный раствор Ag2
SO4
. Сила тока I= 3 A. Время - 2 часа, площадь катода 5 см2
. Электроды платиновые.
Решение:
Распишем все возможные электрохимические реакции, которые могут протекать как на аноде так и па катоде; определим по таблице электродные потенциалы этих реакций.
В растворе находятся следующие ионы: Ag+
, SO2-
4
,
а также нейтральные молекулы воды. Следовательно, на катоде (отрицательно заряженный электрод) могут протекать следующие электрохимические реакции:
Ag+
e<->Agφ=+0,799B,
2Н2
0+2е<-> Н2
↑+2OH φ=-0,413В
на аноде (положительно заряженный электрод):
2SО-2
4
- 2е<->S2
02 -
8
φ=+2,01В,
2Н2
0-4е<->02
↑ +4Н* +
φ = 0,81В.
Необходимо знать, что на аноде легче окисляются те атомы, молекулы, ионы, потенциалы которых в данных условиях наиболее низкие, а на катоде восстанавливаются легче те атомы, ионы, молекулы, потенциалы которых наиболее высокие.
Сопоставление потенциалов показывает, что на катоде происходит восстановление серебра: Ag+
+е<->Ag, а на аноде - окисление воды: 2Н2
О - 4е<->О2
+4Н+
.
Для определения толщины осажденной на катоде пленки серебра запишем объединенное уравнение законов Фарадея:
m= (Э/F) lt,
где Э=A/Z
А - атомный вес,
Z - валентность;
F - постоянная Фарадея.
m=pV=psh,
где р - плотность серебра = 10,5 Г/см3
;
s - площадь катода;
h - толщина пленки.
Отсюда h=AItr/FZps.
Подставляя численные значения, получим толщину осажденной на катоде пленки серебра.
h= 1,6·10-13
м.
1. Епифанов Е.И., Мома Ю.А. "Физические основы конструирования и технологии РЭА и ЭВА" - М. Сов. радио, 1979г. - 352с.
2. О.В. Митрофанов и др. "Физические остовы функционирования изделий микроэлектроники". Серия "Микроэлектроника" М. Высшая школа 1987г.
3. Гусев В.Г., Гусев Ю.М. "Электроника" - М. Высшая школа 1991г. - 622с.
4. Курс химии / Под ред. А.И. Харина - М. Высшая школа 1983г. - 542с.
5. Грушевский Б.С. "Основы электроники и микроэлектроники" Киев. Высшая школа, 1987г. - 384с.
6. Программа, методические указания и контрольные задания по курсу "Физические основы электронных устройств" / Сост. А.Н. Иванов - Северодонецк, СТИ, 2000 - 48 с.
|