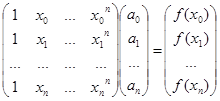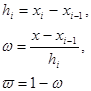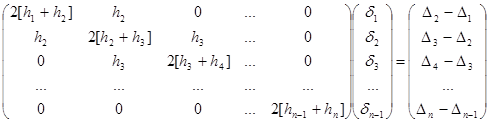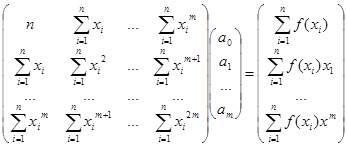Лабораторная работа: Программирование в MATLAB

Кафедра: Информационные технологии

ПРОГРАММИРОВАНИЕ В MATLAB

Операторы MATLAB

· Операторы цикла

Цикл for

Синтаксис

for count=start:step:final

команды MATLAB

end

Описание

count – переменная цикла,

start – ее начальное значение,

final – ее конечное значение,

step – шаг, на который увеличивается count при каждом следующем заходе в цикл

цикл заканчивается, как только значение count становится больше final.

Пример

Пусть требуется вывести семейство кривых для x€ [0, 2π], которое задано функцией, зависящей от параметра

y (x, a) = e^-ax sin x,

для значений параметра а от -0.1 до 0.1. Ниже приведен листинг файл-программы для вывода семейства кривых.

Листинг программы

Figure

x = [0:pi/30:2*pi];

for a = -0.1:0.02:0.1

y = exp (-a*x).*sin(x);

hold on

plot (x, y)

end

В результате выполнения программы появится графическое окно, которое содержит требуемое семейство кривых.

Цикл while

Синтаксис

while условие цикла

команды MATLAB

end

Описание

Цикл работает, пока выполняется (истинно) условие цикла. Для задания условия выполнения цикла допустимы следующие операции отношения:

Задание более сложных условий производится с применением логических операторов. Логические операторы приведены в следующей таблице

Пример

Операторы ветвления

Условный оператор if

Синтаксис

if условие

команды MATLAB

end

Описание

Если условие верно, то выполняются команды MATLAB, размещенные между ifи end, а если условие не верно, то происходит переход к командам, расположенных после end.

Пример

Условный оператор elseif

Синтаксис

if условие1

команды1

elseif условие2

команды2

………………………

elseif условиеn

командыn

else

команды

end

Описание

В зависимости от выполнения того или иного условия работает соответствующая ветвь программы, если все условия неверны, то выполняются команды, размещенные после else.

Пример

Оператор switch

Синтаксис

switch переменная

case значение1

команды1

case значение2

команды2

……………………

caseзначениеn

командыn

otherwise

команды

end

Каждая ветвь определяется оператором case, переход в нее выполняется тогда, когда переменная оператора switch принимает значение, указанное после case, или одно из значение из списка case. После выполнения какой-либо из ветвей происходит выход из switch, при этом значения, заданные в других case, уже не проверяются. Если подходящих значений для переменной не нашлось, то выполняется ветвь программы, соответствующая otherwise.

Пример

Прерывания цикла. Исключительные ситуации.

Оператор break

Синтаксис

break

Оператор break используется при организации циклических вычислений: for…end, while…end. При выполнении условия

if условие

break

end

оператор break заканчивает цикл (for или while) и происходит выполнение операторов, которые расположены в строках, следующих за end. В случае вложенных циклов break осуществляет выход из внутреннего цикла.

Обработка исключительных ситуаций, оператор try … catch

Синтаксис

try

операторы, выполнение которых

может привести к ошибке

catch

операторы, которые следует выполнить

при возникновении ошибки в блоке

между try и catch

end

Описание

Конструкция try…catch позволяет обойти исключительные ситуации (ошибки, приводящие к окончанию работы программы, например, обращение к несуществующему файлу) и предпринять некоторые действия в случае их возникновения.

Пример

Сервисные функции

disp – осуществляет вывод текста или значения переменной в командное окно

input – осуществляет запрос на ввод с клавиатуры. Используется при создании приложений с интерфейсом из командной строки.

eval – выполняет содержимое строки или строковой переменной, как команды MATLAB

clear – удаляет переменные рабочей среды.

с lc – производит очистку командного окна

Более подробную информацию об этих и других функциях можно узнать, выполнив в командной строке

help имя_функции

Задания на выполнение лабораторной работы

Номер конкретного варианта задания определяется преподавателем.

Задание №1

Данное задание подразумевает нахождение для некоторой совокупности данных алгебраического интерполяционного многочлена степени n: P_n ( x ) .

Цель работы:

Необходимо составить программу вычисления коэффициентов алгебраического интерполяционного многочлена P_n ( x )= a ₀ + a ₁ x + … + a_n xⁿ .

Методические указания:

Пусть, например, имеется следующая совокупность данных:

Коэффициенты a ₀ , a ₁ , …, a_n определяются из решения системы уравнений:

Здесь n – порядок интерполяционного многочлена,

n +1 – количество заданных пар точек (x , y ),

a ₀ , a ₁ ,… a_n – искомые коэффициенты многочлена P_n ( x )= a ₀ + a ₁ x + … + a_n xⁿ ).

Требования к программе

При выполнении данной работы необходимо:

· Задать границы отрезка [x0, xn] , на котором строится интерполяционный многочлен P(x)

· Задать n – количество отрезков интерполяции (или, что то же самое, степень многочлена)

Примечание: x0 , xn , n вводятся с клавиатуры.

· Для получения исходных данных (x, y) (количество пар точек (x_i, y_i ) , по которым строится интерполяционный многочлен P(x) – n1=n+1 ) предусмотреть:

- Ввод произвольно расположенных узлов x_i, i=0, n с клавиатуры

- Расчет узлов x_i , i=0, n, соответствующих равномерному расположению аргумента x на отрезке [x0, xn]

- В пп. 1,2 значения y_i , i=0, n либо вводятся с клавиатуры (если исходная функция неизвестна), либо вычисляются по заданной функции f(x) . Выражение, определяющее функцию, вводится с клавиатуры и должно соответствовать правилам записи выражений в MATLAB

- Ввод данных (x_i, y_i, i=0, n ) из файла

· Решить систему уравнений для определения коэффициентов многочлена P(x)

· Построить графики исходной таблично заданной функции и многочлена P(x)

· Если исходные данные заданы в виде функции f(x), построить график погрешности интерполяции /f(x) – P(x)/. Рассчитать максимальное по модулю значение погрешности интерполяции на заданном промежутке.

При выполнении последнего пункта на отрезке [x0, xn] взять не менее 500 точек для проведения расчетов

Задание №2

Интерполяция сплайнами

Цель работы:

Необходимо составить программу вычисления коэффициентов и построения сплайн-функции S(x), «склеенной» из кусков многочленов 3‑го порядка S_i ( x ), которые имеют специальную форму записи:

,

функция S_i ( x ) определена на отрезке [x_{i -1} , x_i ],

Требования к программе

При выполнении данной работы необходимо:

· Задать границы отрезка [x0, xn], на котором строится сплайн-функция S(x)

· Задать n – количество отрезков интерполяции, на каждом из которых строится кубический многочлен Si(x).

· Примечание: x0, xn, n вводятся с клавиатуры.

· Организовать ввод исходных данных (x, y) (количество пар точек (xi, yi), по которым строится сплайн-функция S(x), n1=n+1), предусмотрев:

- Ввод произвольно расположенных узлов xi, i=0, n с клавиатуры

- Расчет узлов xi, i=0, n, соответствующих равномерному расположению аргумента x на отрезке [x0, xn]

- В пп. 1,2 значения yi, i=0, n либо вводятся с клавиатуры (если исходная функция неизвестна), либо вычисляются по заданной функции f(x). Выражение, определяющее функцию, вводится с клавиатуры и должно соответствовать правилам записи выражений в MATLAB

- Ввод данных (xi, yi, i=0, n) из файла

· Для краевых условий 1–3 рассчитать коэффициенты di кубических сплайнов

- S1''(x0)=0, S3''(x3)=0

- S1'(x0)=f '(x0), S3'(x3)=f '(x3)

- S1''(x0)=f «(x0), S3''(x0)=f «(x3)

· Для определения коэффициентов естественного кубического сплайна (краевые условия 1) необходимо решить следующую систему уравнений:

·

Коэффициенты σ₀ =0,σ_n =0

· Построить графики исходной функции и сплайн-функций для всех трех типов краевых условий.

· Построить графики функций погрешности сплайн-интерполяции f(x) – S(x) для всех трех типов краевых условий.

· Рассчитать максимальные по модулю значения погрешности интерполяции на заданном промежутке [x0, xn] для каждого вида сплайна.

Примечание:

В пакете MATLAB индексы одномерных и двумерных массивов начинаются с 1, а не с 0. Учесть это при составлении программы.

Задание №3

Аппроксимация функции методом наименьших квадратов (МНК).

Данное задание подразумевает нахождение для некоторой совокупности данных аппроксимирующей функции (многочлена степени m), построенной методом наименьших квадратов (МНК).

Цель работы:

Необходимо составить программу нахождения коэффициентов многочлена φ( x )= a ₀ + a ₁ * x +… a_n * x^m методом наименьших квадратов.

Рекомендации по выполнению работы:

Пусть, например, имеется следующая совокупность данных:

Поиск необходимых коэффициентов осуществляется следующим образом:

где n – количество точек (x , y ),

m – степень искомого многочлена,

a ₀ , a ₁ , …, a_m – искомые коэффициенты (φ ( x )= a ₀ + a ₁ x + … + a_m x^m ).

Требования к программе

При выполнении данной работы необходимо:

· Задать границы отрезка [x1, xn], на котором строится аппроксимирующая функция φ(x)=a0+a1*x+… an * xm

· Задать m – степень многочлена

· Примечание: x1, xn, m вводятся с клавиатуры.

· Для получения исходных данных (x, y), по которым строится аппроксимирующая функция φ(x)=a0+a1*x+… an* x^m предусмотреть:

- Ввод произвольно расположенных узлов xi, i=1, n с клавиатуры

- Расчет узлов xi, i=1, n, соответствующих равномерному расположению аргумента x на отрезке [x1, xn]

- В пп. 1,2 значения yi, i=1, n либо вводятся с клавиатуры (если исходная функция неизвестна), либо вычисляются по заданной функции f(x). Выражение, определяющее функцию, вводится с клавиатуры и должно соответствовать правилам записи выражений в MATLAB

- Ввод данных (xi, yi, i=1, n) из файла

· Решить систему уравнений для определения коэффициентов многочлена φ(x)

· Построить графики исходной таблично заданной функции и многочлена φ(x)

· Если исходные данные заданы в виде функции f(x), построить график погрешности интерполяции /f(x) – φ(x)/. Рассчитать максимальное по модулю значение погрешности интерполяции на заданном промежутке.

При выполнении последнего пункта на отрезке [x1, xn] взять не менее 500 точек для проведения расчетов

Требования к оформлению лабораторной работы

Отчет должен содержать:

1. Постановку задачи

2. Текст программы

3. Результаты тестирования

Примечание тексты программ должны быть снабжены комментариями.

Список литературы

1. Ануфриев И.Е. Самоучитель Matlab 5.3/6.x – СПб.: БХВ-Петербург, 2003. – 736 с.: ил.

2. В.П. Дьяконов MATLAB 6.5 SPI/7 + Simulink 5/6 в математике и моделировании. Серия «Библиотека профессионала». – М.: СОЛОН-Пресс, 2005. – 576 с.: ил.

3. Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MathLab 7. – СПб.: БХВ-Петербург, 2005. – 1104 с.: ил.