Содержание
Что такое система счисления?
Как порождаются целые числа в позиционных системах счисления?
Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Перевод чисел из одной системы счисления в другую
Сложение в различных системах счисления
Вычитание в различных системах счисления
Умножение в различных системах счисления
Деление в различных системах счисления
Что такое система счисления?
Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления
вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления
вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения:
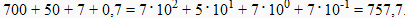
Любая позиционная система счисления характеризуется своим основанием
.
Основание позиционной системы счисления
— количество различных цифр, используемых для изображения чисел в данной системе счисления.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д.
Как порождаются целые числа в позиционных системах счисления?
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением
цифры
называют замену её следующей по величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Применяя это правило, запишем первые десять целых чисел
· в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
· в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
· в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
· в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
| Двоичная система |
Четверичная система |
Восьмеричная система |
Десятичная система |
Шестнадцатиричная система |
| 1 |
1 |
1 |
1 |
1 |
| 10 |
2 |
2 |
2 |
2 |
| 11 |
3 |
3 |
3 |
3 |
| 100 |
10 |
4 |
4 |
4 |
| 101 |
11 |
5 |
5 |
5 |
| 110 |
12 |
6 |
6 |
6 |
| 111 |
13 |
7 |
7 |
7 |
| 1000 |
20 |
10 |
8 |
8 |
| 1001 |
21 |
11 |
9 |
9 |
| 1010 |
22 |
12 |
10 |
A |
| 1011 |
23 |
13 |
11 |
B |
| 1100 |
30 |
14 |
12 |
C |
| 1101 |
31 |
15 |
13 |
D |
| 1110 |
32 |
16 |
14 |
E |
| 1111 |
33 |
17 |
15 |
F |
| 10000 |
40 |
20 |
16 |
10 |
Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами
:
· для ее реализации нужны технические устройства с двумя устойчивыми состояниями
(есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
· представление информации посредством только двух состояний надежно
и помехоустойчиво
;
· возможно применение
аппарата булевой алгебры
для выполнения логических преобразований информации;
· двоичная арифметика намного проще десятичной.
Недостаток двоичной системы
— быстрый рост числа разрядов, необходимых для записи чисел.
Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод чисел из одной системы счисления в другую
Количество p
различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием
системы счисления – "p
"
. Любое число N
в позиционной системе счисления с основанием p
может быть представлено в виде полинома от основания p
:
N = an
pn
+an-1
pn-1
+ ... +a1
p+a0
+a-1
p-1
+a-2
p-2
+ ...
(1.1)
здесь N
– число, aj
– коэффициенты (цифры числа), p
– основание системы счисления (p
>1
). Принято представлять числа в виде последовательности цифр:
N
=
an
an
-1
...
a
1
a
0
.
a
-1
a
-2
...
Перевод чисел в десятичную систему
осуществляется путем составления степенного ряда с основанием той системы (см. формулу 1.1), из которой число переводится. Затем подсчитывается значение суммы.
Перевод целых десятичных чисел в недесятичную систему
счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример:
Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ:
7510
= 1 001 0112
= 1138
= 4B16
.
Перевод правильных дробей из десятичной системы счисления в недесятичную.
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием
необходимо отдельно перевести целую часть и отдельно дробную. Перевести 23.12510
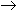 2 с.с. 2 с.с.
| 1. Переведем целую часть: |
2. Переведем дробную часть: |
3. Таким образом: |
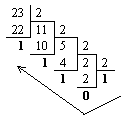 |
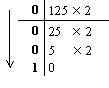 |
2310
= 101112
;
0.12510
= 0.0012
.
Результат:
23.12510
= 10111.0012
.
|
Системы счисления называются кратными
, если выполняется соотношение: S = RN
, где S, R – основания систем счисления, N – степень кратности (целое число: 2, 3 … ).
Для перевода числа из системы счисления
R
в кратную ей систему счисления
S
поступают следующим образом: двигаясь от точки влево и вправо, разбивают число на группы по N
разрядов, дополняя при необходимости нулями крайние левую и правую группы. Затем группу заменяют соответствующей цифрой из системы счисления S
.
Таблица
Перевести 1101111001.11012
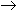 "8" с.с. "8" с.с. |
Перевести 11111111011.1001112
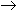 "16" с.c. "16" с.c. |
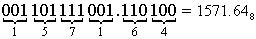 |
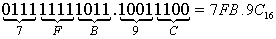 |
Для перевода числа из системы счисления
S
в кратную ей систему счисления
R
достаточно заменить каждую цифру этого числа соответствующим числом из системы счисления R
, при этом отбрасывают незначащие нули в старших (00
512) и младших (15,124000
) разрядах.
Перевести 305.48
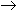 "2" с.с. "2" с.с. |
Перевести 7B2.E16
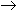 "2" с.с. "2" с.с. |
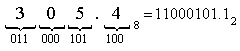 |
 |
Если требуется выполнить перевод из системы счисления S
в R
,
при условии что они не являются кратными
, тогда нужно попробовать подобрать систему счисления K
, такую что: S =
K
N
и R
=
K
N
.
Перевести 175.248
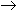 "16" с.с. "16" с.с.
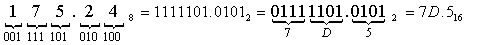
Результат: 175.248
= 7D.516
.
Если систему счисления K подобрать не удается, тогда следует выполнить перевод используя в качестве промежуточной десятичную
систему счисления.
Для всего этого примеры
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему
очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:

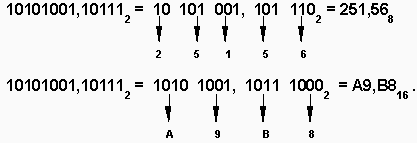
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную,
его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. Например:
Сложение в различных системах счисления
Таблицы сложения легко составить, используя Правило Счета.






Вычитание в различных системах счисления

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.



Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

|