| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ
УНИВЕРСИТЕТ
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
О КАТЕГОРИИ МНОЖЕСТВ
Выполнила студентка V курса
математического факультета
Одегова В.Н.
 /подпись/ /подпись/
Научный руководитель:
Доктор ф.-м.н., профессор
Вечтомов Е.М.
/подпись/
Рецензент: кандитат ф.-м.н., доцент Чермных В.В.
 /подпись/ /подпись/
Допущен к защите в ГАК
 Зав. кафедрой Вечтомов Е.М. Зав. кафедрой Вечтомов Е.М.
(подпись)
  2003г. 2003г.
 Декан факультета Варанкина В.И. Декан факультета Варанкина В.И.
(подпись)
  2003г. 2003г.
Киров, 2003г.
введение.. 3
1 Основные понятия теории категорий.. 4
1.1. Мономорфные стрелки. 6
1.2. Эпиморфные стрелки. 7
1.3. Изострелки. 8
1.5. Начальные объекты.. 10
1.6. Конечные объекты.. 10
1.7. Двойственность. 11
1.8. Произведения. 12
1.9. Произведение отображений. 15
1.10. Копроизведение объектов. 18
2 категориЯ множеств.. 19
2.1. Мономорфизм в категории множеств. 20
2.2. Эпиморфизм в категории множеств. 21
2.3. Начальные и конечные объекты в категории множеств. 23
2.4. Произведение в категории множеств. 23
2.5. Копроизведения в категории множеств. 24
3 Примеры категорий.. 24
3.1. Категория 1. 24
3.2. Категория 2. 25
3.3. Категория 3. 25
3.4. Категории предпорядка. 26
3.5. Дискретные категории. 26
3.6. Категория N.. 27
Литература.. 28
Для того чтобы проиллюстрировать формализацию интуитивной математической идеи рассмотрим понятие функции.
Функция – есть связь между объектами. Точнее, это – соответствие, сопоставляющее заданному объекту точно один другой объект.
Если А – множество всех возможных входов функции f, а В – множество, включающее все f-образы элементов из А, то говорят, что f является функцией из множества А во множество В. Это выражают записью f: A®B.
Множество А называется областью определения, а множество В – областью значений.
В общей теории категорий вместо слова «функция» используют более нейтральное слово «стрелка» (а также слово «морфизм»).
Выполняются следующие свойства:
1. C каждой стрелкой связано два специальных объекта – её начало и конец.
2. Имеется операция композиции, которая применяется к определенным парам ‹ g, ¦› стрелок данной категории (когда область значения первой совпадает с областью определения второй) и дает в результате новую стрелку g˚¦, также принадлежащую данной категории.
3. С каждым объектом данной категории связана специальная стрелка – единичная, или тождественная, стрелка этого объекта.
Итак, дадим аксиоматическое определение категории
.
Категория Ω включает в себя:
1) Совокупность предметов, называемых Ω - объектами
2) Совокупность предметов, называемых Ω-стрелками
3) Операции, ставящие в соответствие каждой Ω-стрелке f Ω-объект dom f (начало стрелки f) и Ω-объект cod f (конец стрелки f). То, что а=domf и b=cod f изображается так: f: a®b
4) Операцию, ставящую в соответствие каждой паре ‹ g, ¦› Ω-стрелок с dom g=cod f Ω-стрелку g˚¦, композицию f и g, с dom (g˚¦)=dom f и cod(g˚¦)=cod g, причем выполняется следующее условие:
закон ассоциативности
:
пусть f: a®b
g: b®c
h: c®d
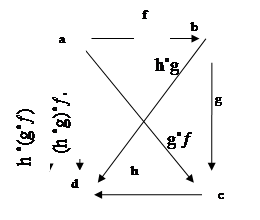 тогда h ˚(g˚¦)= (h ˚g)˚¦. тогда h ˚(g˚¦)= (h ˚g)˚¦.
Закон ассоциативности утверждает, что диаграмма вида -
-коммутативна.
( в теории категорий удобным средством являются коммутативные диаграммы. Диаграмма – это схема, в которой указаны объекты и стрелки между ними. При этом, любые два пути, ведущие по стрелкам из одного объекта в другой, равны. Диаграмма называется коммутативной, если есть несколько путей от одного объекта к другому, то все они приводят к одному и тому же результату. Точнее: диаграмма называется коммутативной, когда все возможные треугольники, составляющие части данной диаграммы, коммутативны. Это означает, что любые два пути стрелок данной диаграммы, начинающиеся в одном и том же объекте и заканчивающиеся в одном и том же объекте, задают в композиции одну и ту же функцию. Диаграммы в теории категорий используются для наглядности изложения.)
5) Сопоставление каждому Ω-объекту b Ω-стрелки 1b
: b®b, называемой единичной или тождественной стрелкой, так что выполнен Закон тождества:
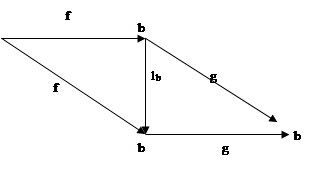 для любых Ω-стрелок f:a®b и g:b®c 1b
◦f=f и g◦1b
=g, т.е. коммутативна диаграмма для любых Ω-стрелок f:a®b и g:b®c 1b
◦f=f и g◦1b
=g, т.е. коммутативна диаграмма
Определение:
Стрелка f:a®b в категории Ω называется мономорфной
или монострелкой в Ω
, если для любой пары g,h: c®a Ω-стрелок из равенства f °g=f ° h следует g=h.
· В произвольной категории композиция
g
°
f
является монострелкой, если как
f
, так и
g
мономорфны
.
Доказательство:
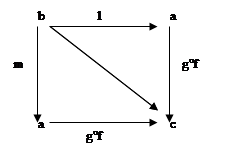 Воспользуемся определением монострелки: Воспользуемся определением монострелки:
 Стрелка g°f:a®c является монострелкой, если для любых стрелок l,m:b®a если (g°f)°l=(g°f)°m, то l=m. Изобразим диаграмму. Очевидно, что требуемое равенство выполняется, т.е. (g°f)°l=(g°f)°m. В любой категории должен выполняться ассоциативный закон. Применяя его, получаем следующее равенство: g°(f°l)=g°(f°m). Стрелка g°f:a®c является монострелкой, если для любых стрелок l,m:b®a если (g°f)°l=(g°f)°m, то l=m. Изобразим диаграмму. Очевидно, что требуемое равенство выполняется, т.е. (g°f)°l=(g°f)°m. В любой категории должен выполняться ассоциативный закон. Применяя его, получаем следующее равенство: g°(f°l)=g°(f°m).
 g – монострелка Þ f °l=f °m g – монострелка Þ f °l=f °m
f – монострелка Þl=m, что и требовалось доказать.
· В произвольной категории, если композиция
g
°
f
– мономорфна, то и
f
– мономорфна.
Доказательство:
пусть f: a®b
g: b®d,
l, m: c®a
f – мономорфна, если из равенства f °l=f °m (*)следует, что l=m.
 Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что domg = cod(f °l) = cod(f °m), применим к равенству (*) стрелку g. Получаем g°(f ° l)=g°(f °m). Далее, по ассоциативному закону: Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что domg = cod(f °l) = cod(f °m), применим к равенству (*) стрелку g. Получаем g°(f ° l)=g°(f °m). Далее, по ассоциативному закону:
 (g°f)°l=(g°f)°m. (g°f)°l=(g°f)°m.
g°f – монострелка Þl=m, что и требовалось доказать.
Определение:
Стрелка f:a®b называется эпиморфной
или эпистрелкой в категории
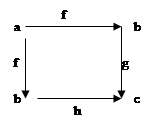 Ω
, если для произвольной пары стрелок g,h: b®c из равенства g°f=h°f следует g=h, т.е. если коммутативна диаграмма, то g=h. Ω
, если для произвольной пары стрелок g,h: b®c из равенства g°f=h°f следует g=h, т.е. если коммутативна диаграмма, то g=h.
· Если
g
°
f
-эпистрелка, то
g
- эпистрелка.
Доказательство:
пусть f: a®b
g: b®c,
l, m: c®d
g – эпистрелка, если из равенства l °g=m °g (*)следует, что l=m.
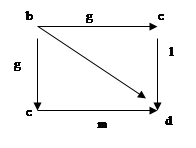  Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что codf = dom(l °g) = dom(m °g), применим к равенству (*) стрелку f. Получаем (l ° g)°f=(m ° g)°f. Далее, по ассоциативному закону: Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что codf = dom(l °g) = dom(m °g), применим к равенству (*) стрелку f. Получаем (l ° g)°f=(m ° g)°f. Далее, по ассоциативному закону:
 l°(g°f)=m°(g°f). l°(g°f)=m°(g°f).
g°f – эпистрелка Þl=m, что и требовалось доказать.
Определение:
произвольная стрелка f: a®b называется изострелкой
или обратимой в категории Ω
стрелкой, если существует Ω- стрелка g:b®a, такая, что g°f=1a
и f°g=1b
.
На самом деле такая стрелка только одна. Действительно, если предположить, что существует ещё одна такая стрелка g’, то g’=1a
°g’=(g°f)°g’=g°(f°g’)=g°1b
=g. Стрелка g, когда она существует, называется обратной к f стрелкой и обозначается f -1
:b®a. Она определяется условиями: f -1
°f=1a
, f °f -1
=1b
.
· Любая изострелка является эпистрелкой.
Доказательство:
пусть f: a®b – изострелка, и стрелки g,h: b®c.
Тогда g °f=h °f и существует f -1
. Тогда g = g °1b
= g °(f °f-1
) =(ассоциативность)= (g °f) °f-1
= (h°f)°f-1
=h °(f °f -1
)=h °1b
=h. Таким образом, f – сократима справа. Ч.т.д.
· Любая изострелка является монострелкой
. (доказательство аналогично предыдущему).
· Любая изострелка является бистрелкой (эпи и монострелкой ).
Доказательство
: следует из предыдущих двух утверждений.
· Каждая единичная стрелка является изострелкой.
Доказательство:
Пусть f: a®a – единичная стрелка. Существует стрелка f –1
: a®a и f –1
°f=1a
, f °f –1
=1a
.Þ f – изострелка. Ч.т.д.
· Если
f
– изострелка, то
f
–1
– изострелка.
Доказательство:
пусть f: a®b – изострелка. Тогда f –1
: b®a. f – изострелка Þ f °f –1
=1b
, f –1
°f=1a
. Þ f –1
– изострелка. Ч.т.д.
· Если
f
,
g
– изострелки, то
f
°
g
– изострелка, при этом (
f
°
g
)- 1
=
g
–1
°
f
-
1
Доказательство:
пусть f: b®c, g: a®b. f °g: a®c. f,g- изострелки Þ $ f –1
: c®b и $ g –1
: b®a Þ$ g –1
°f –1
:c®a. Эта композиция является «подозрительной» на обратную к стрелке f °g. Проверим это:
1) (g –1
°f –1
)°(f °g)=(ассоциативность)=g –1
°(f –1
°f °g)=g–1
°(1b
°g)=g–1
°g=1a
.
2) (f °g )°g –1
° f –1
=f °(g °g –1
°f –1
)=f °(1b
°f –1
)=f °f –1
=1c.
Þ f°g- изострелка и (f °g)-1
=g –1
°f –1
.Ч.т.д.
1.4. Изоморфные объекты
Определение:
Объекты a и b называются изоморфными в Ω
(символически a@b), если существует Ω – стрелка f:a®b, являющаяся изострелкой в Ω, т.е. f: a@b.
· Произвольные Ω – объекты обладают следующими свойствами:
1)
a
@
a
2)
если
a
@
b,
то
b
@
a
3)
если
a
@
b
и
b
@
с, то
a
@
c
Доказательство:
1) в любой категории существует стрелка 1a
: a®a (по определению категории). Единичная стрелка является изострелкой (доказано выше). Получаем, что a@a (по определению изоморфных объектов).
2) a@b Þ$ f :a®b и f – изострелка Þ $ f –1
: b®a (по определению изострелки). Ранее доказано, что если f - изострелка, то и f –1
– изострелка. Т.е. f –1
: b®a – изострелка Þ b@a (по определению изоморфных объектов).
3) a@b Þ$ f :a®b – изострелка.
b@с Þ$ g :b®c – изострелка.
Dom g=cod f Þ $ g °f: a®c и g °f – изострелка (т.к.f и g – изострелки (доказано выше)). Чтобы доказать, что a@c, необходимо найти изострелку t: a®c. Возьмем в качестве такой изострелки t изострелку g °f. Ч.т.д.
Определение:
объект 0 называется начальным
в категории Ω, если для каждого объекта а из Ω существует одна и только одна Ω – стрелка из 0 в а.
· Любые два начальных объекта изоморфны в Ω.
Доказательство:
Предположим, что 0 и 0’- начальные объекты. Требуется доказать, что 0@0’. Для этого необходимо найти изострелку 0®0’.
Существуют единственные стрелки f: 0’®0 (т.к.0’ - начальный объект) и g: 0®0’ (т.к. 0 – начальный объект). Dom f=cod g Þ$ f °g: 0®0. 0 – начальный объект Þ $! стрелка 0®0. и по определению категории для каждого Ω – объекта $ единичная стрелка. Значит стрелка 10
: 0®0 и стрелка f °g:0®0 совпадают. Аналогично, стрелка g °f:0’®0’ совпадает со стрелкой 10’
. Тогда g имеет обратную стрелку (а именно f), т.е. g: 0@0’. Ч.т.д.
Обращая направление стрелок в определении начального объекта, получаем следующее определение.
Определение:
объект 1 называется конечным
в категории Ω, если для каждого Ω – объекта а существует одна и только одна стрелка из а в 1.
· Все конечные объекты изоморфны
.
Доказательство:
Предположим, что 1 и 1’ – конечные объекты. Требуется доказать, что 1@1’. Для этого надо найти изострелку 1®1’.
Объект 1 – конечный Þ $! f: 1’®1 (по определению конечного объекта).
Объект 1’ - конечный Þ$! g:1®1’ ( по той же причине). Dom f=cod g Þ $ f °g :1®1.
1 – конечный объект. Þ f °g: 1®1 – единственная.
С другой стороны для любого объекта категории существует единичная стрелка 11
:1®1. Значит f °g=11
. Аналогично, g °f=11’
. Таким образом, для стрелки g нашлась обратная (а именно f), т.е.g: 1@1’. Ч.т.д.
· Стрелка
f:1
®
a – мономорфна.
Доказательство:
F: 1®a – мономорфна, если для любых стрелок g,h:b®1 из того, что f °g=f °h следует, что g=h. Но по определению конечного объекта, существует только одна стрелка b®1. Поэтому равенство стрелок g и h следует автоматически.
Можно заметить, что понятие эпистрелки получается из определения монострелки «обращением стрелок». То же справедливо для понятий конечного и начального объектов. Эти два примера иллюстрируют понятие двойственности
в теории категорий.
Если å- предложение категорного языка, то двойственным åор
назовем предложение, получаемое из å заменой «dom» на «cod», «cod» на«dom» и «h=g °f» на «h=f °g». Таким образом, все стрелки и композиции, входящие в å ,повернуты в åор
в другую сторону. Понятие, описываемое предложением åор
называется двойственным к понятию, описываемому å. Для данной категории Ω построим двойственную категорию Ωор
следующим образом.
Категории Ω и Ωор
имеют одни и те же объекты. Для каждой f:a®b вводим Ω- стрелку fop
:b®a (свою для каждой f). Так получаемые стрелки  исчерпывают все стрелки категории Ωор
. Композиция fop
°gop
определена тогда и только тогда, когда определена в Ω композиция g°f и fop
°gop
=(g°f)op
. Dom fop
=cod f и codfop
=dom f. исчерпывают все стрелки категории Ωор
. Композиция fop
°gop
определена тогда и только тогда, когда определена в Ω композиция g°f и fop
°gop
=(g°f)op
. Dom fop
=cod f и codfop
=dom f.
Конструкцию, двойственную к выражаемой предложением å, можно интерпретировать как первоначальное построение, примененное к двойственной категории. Если å истинно в Ω, то åор
истинно в Ωор
. Т.о. из произвольного истинного в теории категорий предложения получается другое истинное предложение åор
. В этом состоит принцип двойственности
. Принцип двойственности сокращает количество доказательств вдвое. Так, доказав, что два произвольных начальных объекта изоморфны, можно сразу утверждать, что два произвольных конечных объекта изоморфны.
Как охарактеризовать произведение двух множеств
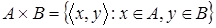 с помощью стрелок. Неужели это можно сделать без какого-то использования упорядоченных пар? с помощью стрелок. Неужели это можно сделать без какого-то использования упорядоченных пар?
Оказывается это возможно. Способ, позволяющий избежать использования упорядоченных пар, даст возможность выяснить, что такое конструкция в теории категорий.
Поставим в соответствие произведению 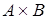 два специальных отображения (проекции) два специальных отображения (проекции)
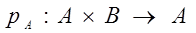 и и  , задаваемые равенствами , задаваемые равенствами 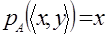 , , 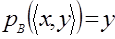 . .
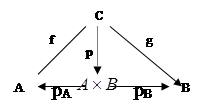 Допустим теперь, что задано ещё одно множество С с парой отображений f: C®A, g: C®B. Определим отображение p: C® Допустим теперь, что задано ещё одно множество С с парой отображений f: C®A, g: C®B. Определим отображение p: C® правилом p(x)= правилом p(x)=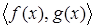 , ,
Тогда
pА
(p(x))=f(x) и pB
(p(x))=g(x) для каждого хÎС. Таким образом, pA
°p=f и pB
°p=g, т.е. приведенная выше диаграмма коммутативна. Более того, p является единственной стрелкой, для которой эта диаграмма коммутативна. Действительно, если p(x)=<y,z>, то в силу условия pA
°p=f будет pA
(p(x))=f(x), т.е. y=f(x). Аналогично, если pB
°p=g, то z=g(x).
Отображение p, построенное по f и g, обозначаются обычно через <f,g> и называется произведением отображений f и g.
Эти рассмотрения служат мотивировкой для следующего определения.
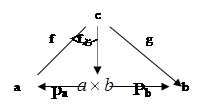 Определение:
произведением
в категории Ω двух объектов a и b называется Ω-объект, обозначаемый через Определение:
произведением
в категории Ω двух объектов a и b называется Ω-объект, обозначаемый через 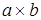 , вместе с парой (pra
: , вместе с парой (pra
: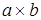 ®a, prb
: ®a, prb
: ®b) Ω- стрелок, такой, что для произвольной пары (f:c®a, g:c®b) Ω- стрелок существует одна и только одна стрелка <f,g>:c® ®b) Ω- стрелок, такой, что для произвольной пары (f:c®a, g:c®b) Ω- стрелок существует одна и только одна стрелка <f,g>:c® , для которой диаграмма коммутативна, т.е. pra
°<f,g>=f и prb
°<f,g>=g. Стрелка <f,g> называется произведением стрелок f и g относительно проекций pra
,prb
. , для которой диаграмма коммутативна, т.е. pra
°<f,g>=f и prb
°<f,g>=g. Стрелка <f,g> называется произведением стрелок f и g относительно проекций pra
,prb
.
· <
pra
,
prb
>=1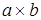 .
.
 Доказательство:
изобразим данную ситуацию на диаграмме.(точнее левую часть доказываемого равенства). Видим, что стрелка <pra
,prb
> переводит объект Доказательство:
изобразим данную ситуацию на диаграмме.(точнее левую часть доказываемого равенства). Видим, что стрелка <pra
,prb
> переводит объект 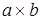 в объект в объект  . А по определению категории существует только одна единичная стрелка (та, которая переводит объект категории в себя). Значит, эти стрелки совпадают. Ч.т.д. . А по определению категории существует только одна единичная стрелка (та, которая переводит объект категории в себя). Значит, эти стрелки совпадают. Ч.т.д.
· Если <
f
,
g
>=<
k
,
h
>, то
f
=
k
и
g
=
h
.
Доказательство
: разберемся с условием утверждения.
a) Стрелка <f,g> существует по условиюÞdomf=domg. Пусть f:c®a, g:c®b. тогда стрелка <f,g>:c®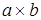 . .
b) Стрелка <k,h> совпадает со стрелкой <f,g> по условию. Þ dom<k,h>=dom<f,g>=c, cod<k,h>=cod<f,g>=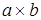 . Þстрелки k,h такие, что domk=domh=c, а концы этих стрелок в объектах a и b. . Þстрелки k,h такие, что domk=domh=c, а концы этих стрелок в объектах a и b.
c) Предположим, что k:c®b, h:c®a. Если это так, то стрелка <k,h>:c® . Тогда <k,h>¹<f,g>, так как у них не совпадают концы. . Тогда <k,h>¹<f,g>, так как у них не совпадают концы.
d) Получили противоречие после того, как предположили, что k:c®b, h:c®a. остается один вариант: k:c®a, h:c®b. значит f=k, g=h. Ч.т.д.
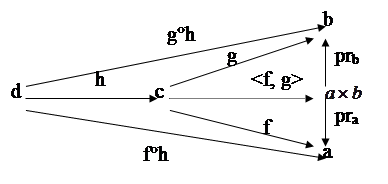
· <f
°
h, g
°
h>=<f,g>
°
h
 Доказательство:
Посмотрим, что означает стрелка <f°h, g°h>. Во-первых: композиция двух стрелок существует, когда конец одной стрелки является началом другой. Из условия следует, что domf=codh и domg=codh, а также dom<f,g>=codh. Т.е. стрелки f, g, <f,g> имеют одно и то же начало. Пусть h: d®c, g:c®b, f:c®a. Изобразим диаграмму: эта диаграмма коммутативна, т.е. pra
°<f,g>°h=f°h и prb
°<f,g>°h=g°h. Произведением стрелок f°h, g°h является однозначно-определенная стрелка (она единственна по определению произведения). И этой стрелкой является композиция стрелок <f,g> и h. Доказательство:
Посмотрим, что означает стрелка <f°h, g°h>. Во-первых: композиция двух стрелок существует, когда конец одной стрелки является началом другой. Из условия следует, что domf=codh и domg=codh, а также dom<f,g>=codh. Т.е. стрелки f, g, <f,g> имеют одно и то же начало. Пусть h: d®c, g:c®b, f:c®a. Изобразим диаграмму: эта диаграмма коммутативна, т.е. pra
°<f,g>°h=f°h и prb
°<f,g>°h=g°h. Произведением стрелок f°h, g°h является однозначно-определенная стрелка (она единственна по определению произведения). И этой стрелкой является композиция стрелок <f,g> и h.
Для данных теоретико-множественных функций f:A®B и g:C®D определим функцию 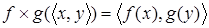 . . 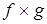 является произведением двух композиций: является произведением двух композиций: 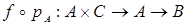 и и  . Поэтому дадим следующее определение. . Поэтому дадим следующее определение.
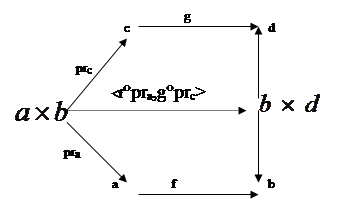 Определение:
если f:a®b и g:c®d – две Ω-стрелки, то через Определение:
если f:a®b и g:c®d – две Ω-стрелки, то через 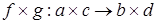 обозначим Ω-стрелку обозначим Ω-стрелку  . .
· 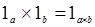
 Доказательство:
представим ситуацию диаграммой. По определению произведения стрелок стрелка Доказательство:
представим ситуацию диаграммой. По определению произведения стрелок стрелка 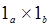 :
:
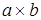 ® ®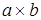 , и эта стрелка единственна. А по определению категории, у каждого объекта существует единичная стрелка, т.е. та, которая переводит объект в себя. Значит стрелки , и эта стрелка единственна. А по определению категории, у каждого объекта существует единичная стрелка, т.е. та, которая переводит объект в себя. Значит стрелки  и
и 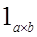 совпадают. Ч.т.д. совпадают. Ч.т.д.
· 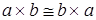
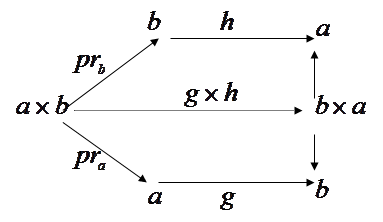 Доказательство:
для того, чтобы доказать изоморфизм двух объектов, необходимо найти изострелку. В нашем случае изострелку f: Доказательство:
для того, чтобы доказать изоморфизм двух объектов, необходимо найти изострелку. В нашем случае изострелку f: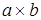 ® ® . Для существования произведения . Для существования произведения 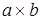 необходимо иметь две стрелки. Пусть g:a®b, h:b®a. тогда необходимо иметь две стрелки. Пусть g:a®b, h:b®a. тогда 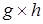 : :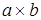 ® ®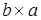 . Эта стрелка единственна по определению произведения. Изобразим диаграмму. . Эта стрелка единственна по определению произведения. Изобразим диаграмму.
А теперь рассмотрим стрелку  . Предположительно, эта стрелка является обратной к стрелке . Предположительно, эта стрелка является обратной к стрелке 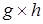 . (эта стрелка тоже единственна по определению произведения). Действительно, композиция ( . (эта стрелка тоже единственна по определению произведения). Действительно, композиция (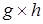 )°( )°( ): ): ® ® . Так как стрелки . Так как стрелки 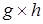 и и  - единственны, то и их композиция есть единственная стрелка. А по определению категории, каждый объект имеет единичную стрелку. Поэтому, ( - единственны, то и их композиция есть единственная стрелка. А по определению категории, каждый объект имеет единичную стрелку. Поэтому, ( )°( )°( )= )=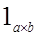 . Аналогично ( . Аналогично ( )°( )°(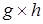 )= )=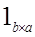 . Значит, по определению изострелки, стрелка . Значит, по определению изострелки, стрелка 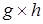 является изострелкой. Þ является изострелкой. Þ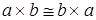 (по определению изоморфности двух объектов). Ч.т.д. (по определению изоморфности двух объектов). Ч.т.д.
· 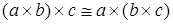
Доказательство:
для доказательства этого утверждения построим диаграмму.
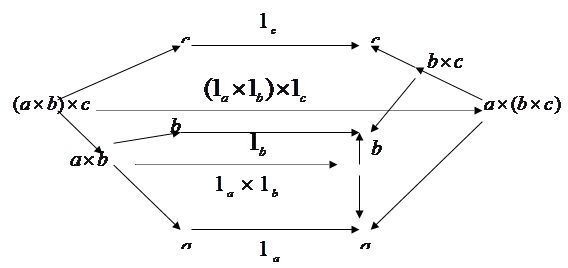
Стрелка 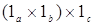 : : . Если рассмотреть подобную диаграмму (в которой . Если рассмотреть подобную диаграмму (в которой 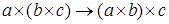 ), то получим стрелку ), то получим стрелку 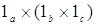 . Эта стрелка является обратной к стрелке . Эта стрелка является обратной к стрелке 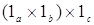 . (проверяется аналогично). Значит . (проверяется аналогично). Значит 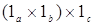 - изострелка. Þ Þ - изострелка. Þ Þ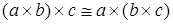 . Ч.т.д. . Ч.т.д.
· 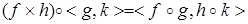
Доказательство:
a)
так как существует композиция 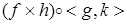 , то dom , то dom =cod =cod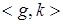 . .
b)
Так как существует стрелка 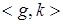 , то domg=domk. , то domg=domk.
c)
Из существования стрелки 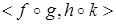 следует, что dom(f°g)=dom(h°k), domf=codg, domh=codk. следует, что dom(f°g)=dom(h°k), domf=codg, domh=codk.
d)
Изобразим диаграмму. Композиция 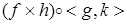 :с® :с®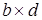 . .
e)
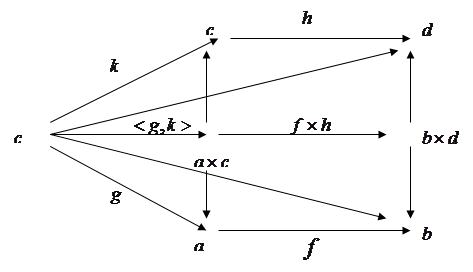  :с® :с®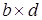 . А по определению произведения объектов стрелка . А по определению произведения объектов стрелка  - единственна. Значит стрелки <f°g,h°k> и - единственна. Значит стрелки <f°g,h°k> и  совпадают. Ч.т.д. совпадают. Ч.т.д.
Понятие копроизведения, или суммы объектов, является двойственным к понятию произведения. Его определение получается непосредственно из определения произведения по принципу двойственности.
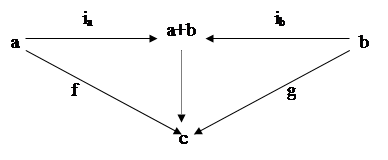 Определение:
копроизведением
в категории Ω двух объектов a и b называется Ω-объект, обозначаемый через a+b, вместе с парой (ia
:a®a+b, ib
:b®a+b) -стрелок, такой, что для произвольной пары (f:a®c, g:b®c) –стрелок существует одна и только одна стрелка [f,g]:a+b®c, для которой диаграмма коммутативна, т.е. [f,g]°ia
=f, [f,g]°ib
=g. Стрелка [f,g] называется копроизведением
стрелок f,g относительно инъекций ia
и ib
. Определение:
копроизведением
в категории Ω двух объектов a и b называется Ω-объект, обозначаемый через a+b, вместе с парой (ia
:a®a+b, ib
:b®a+b) -стрелок, такой, что для произвольной пары (f:a®c, g:b®c) –стрелок существует одна и только одна стрелка [f,g]:a+b®c, для которой диаграмма коммутативна, т.е. [f,g]°ia
=f, [f,g]°ib
=g. Стрелка [f,g] называется копроизведением
стрелок f,g относительно инъекций ia
и ib
.
Можно посмотреть длинный список категорных вариантов математических конструкций и понятий. Мы уже имеем некоторое представление о том, как теория категорий воссоздает мир математических идей и в действительности раздвигает горизонты математического мышления. Мы познакомились немного с категорией множеств.
Пусть S-класс всевозможных множеств, рассматриваемых с отображениями одних множеств в другие.
f:A→B обозначается отображение множества А во множество В.
Композицией
отображений f:A→B и g:B→C, называется отображение g °f:A→C, вычисляемое по формуле:  g°f(a)=g(f(a)). Эта частичная бинарная операция композиция отображений ассоциативна (там, где определена). Проверяется это так: g°f(a)=g(f(a)). Эта частичная бинарная операция композиция отображений ассоциативна (там, где определена). Проверяется это так:
даны отображения f:A→B, g:B→C, h:C→D. h°(g°f)=(h°g)°f. Обе части определены. Возьмем  . Преобразуем левую часть: h°(g°f)(а)=h°(g°f(a))=h°(g(f(a)))=h(g(f(a))). Преобразуем правую часть: ((h°g)°f)(а)=(h°g)°f(a)=(h°g)(f(a))=(h°g(f(a)))=h(g(f(a))).левая и правая части равны.Þ h°(g°f)=(h°g)°f.Þкомпозиция ассоциативна. . Преобразуем левую часть: h°(g°f)(а)=h°(g°f(a))=h°(g(f(a)))=h(g(f(a))). Преобразуем правую часть: ((h°g)°f)(а)=(h°g)°f(a)=(h°g)(f(a))=(h°g(f(a)))=h(g(f(a))).левая и правая части равны.Þ h°(g°f)=(h°g)°f.Þкомпозиция ассоциативна.
 1А
:А→А, что 1А
:А→А, что 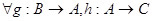 справедливы равенства: справедливы равенства:
1) 1А
°g=g
2) h°1A
=h
получили конкретную категорию множеств (категория Set).
В категории множеств объектами являются все множества, а стрелками – все функции между множествами. Выполняются следующие свойства:
1. С каждой стрелкой связано два специальных объекта – её начало и конец.
2. Имеется операция композиции, которая применяется к определенным парам ‹ g, ¦› стрелок данной категории (когда область значения первой совпадает с областью определения второй) и дает в результате новую стрелку g˚¦, также принадлежащую данной категории.
3. С каждым объектом данной категории связана специальная стрелка – единичная, или тождественная, стрелка этого объекта.
· В категории Set (категория множеств) для любого отображения f:A→B эквивалентны условия:
1) f- мономорфизм
2) f-инъекция
3) g°f=1A
для некоторого g:B→A
Доказательство:
поведем по циклу 1)→2)→3)→1)
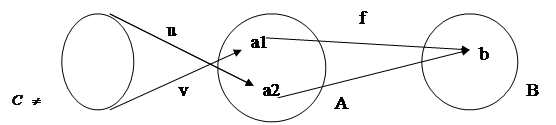 1)→2): предположим, что мономорфизм f не является инъективным отображением, т.е. 1)→2): предположим, что мономорфизм f не является инъективным отображением, т.е.  в А и f(a1)=f(a2)=b. в А и f(a1)=f(a2)=b.
Возьмем произвольное непустое множество С и два отображения u:C→A, v:C→A, такие, что при отображении v множество С переходит в элемент а1ÎА, а при отображении u множество С переходит в элемент а2ÎА. Заметим, что u¹v. Тогда ,нетрудно видеть, что f°u=b=f°v. но f – мономорфнаÞu=v. Пришли к противоречию, после того, как предположили, что f- не инъективнаÞf – инъективна.
 2)→3) Пусть f-инъекция. Для доказательства необходимо найти отображение g:B→A. зададим отображение g правилом: 2)→3) Пусть f-инъекция. Для доказательства необходимо найти отображение g:B→A. зададим отображение g правилом:
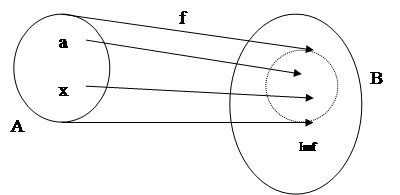 g(b)= g(b)=
Тогда, очевидно, что g°f=1A
.
3)→1) в произвольной категории доказано свойство о том, что если заданы отображения f:A→B, g:B→A, то из того, что g°f - мономорфизм следует, что f-мономорфизм. По условию g°f=1А
. Выше также доказано свойство о том, что любая единичная стрелка является монострелкой . Из всего вышесказанного следует, что f – мономорфизм. Теорема доказана полностью.
· В категории Set (категория множеств) для любого отображения f:A→B эквивалентны условия:
1) f- эпиморфизм, 2) f-сюръекция, 3) f°g=1B
для некоторого g:B→A
Доказательство
:
доказательство поведем по циклу 1)→2)→3)→1)
1)→2) пусть f – эпиморфизм. Предположим, что отображение f не является отображением «на», т.е. не является сюръекцией. (Imf¹B).
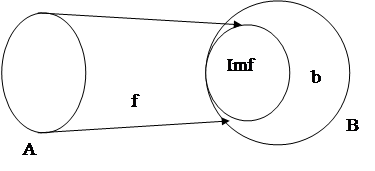 Возьмем b1ÎB\Imf. Возьмем b1ÎB\Imf.
Пусть С={b1,b2}. Возьмем отображения u:B→C, такое, что любой элемент из В переходит в b2. отображение v:B→C зададим следующим образом:
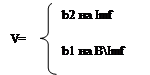
Заметим, что u и v не совпадают. Тогда u°f=b=v°f. Так как f-эпиморфизм (по условию)Þu=v. Получили противоречие после того, как предположили, что f не является сюрьекцией. Значит, f – сюрьекция.
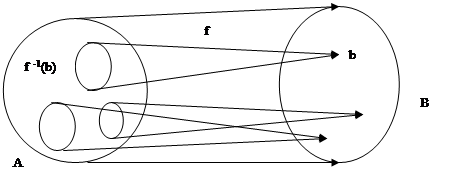 2)→3) пусть f- сюрьекция. 2)→3) пусть f- сюрьекция.
сюьективность означает, что 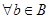 его прообраз не пуст. По аксиоме выбора: существует отображение g:B→ его прообраз не пуст. По аксиоме выбора: существует отображение g:B→ . Тогда f °g=1B
. Ч.т.д. . Тогда f °g=1B
. Ч.т.д.
3)→1) в произвольной категории доказано свойство о том, что если заданы отображения f:A→B, g:B→A, то из того, что g°f – эпиморфизм следует, что g-эпиморфизм (док-во см. выше). По условию g°f=1В
. Выше также доказано свойство о том, что любая единичная стрелка является эпистрелкой . Из всего вышесказанного следует, что g – эпиморфизм. Теорема доказана полностью.
Следствие: в категории
Set
эквивалентны следующие условия:
f
-бистрелка,
f
-биекция,
f
-изоморфизм.
В категории множеств начальным объектом является пустое множество, так как пустое множество есть подмножество любого множества. Стрелкой можно мыслить пары (элементу одного множества сопоставляется элемент другого). Таким образом, сопоставляя пустому множеству элемент любого множества, получим пустое множество пар, которое является единственным.
Конечными объектами в категории множеств являются одноэлементные множества. Для данного множества А правило f(x)=e определяет функцию f:A→{e}. Так как e является единственным возможным значением, то эта функция является единственной такой функцией. Таким образом, Set имеет много конечных объектов. Все они изоморфны между собой (конечные объекты изоморфны в любой категории). Их представителем является одноэлементное множество {0}.
 В теории множеств есть понятие прямого произведения множеств. Это такое множество В теории множеств есть понятие прямого произведения множеств. Это такое множество 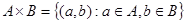 . Существуют естественные отображения – проекции . Существуют естественные отображения – проекции 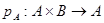 и и  , такие, что pA
(a,b)=a , pB
(a,b)=b. Прямое отображение удовлетворяет свойству универсальности: для любых множеств А, В, С и отображений f:C→A и g:C→B существует единственное отображение h: , такие, что pA
(a,b)=a , pB
(a,b)=b. Прямое отображение удовлетворяет свойству универсальности: для любых множеств А, В, С и отображений f:C→A и g:C→B существует единственное отображение h:  , делающее диаграмму (*) коммутативной. , делающее диаграмму (*) коммутативной.
Легко видеть, что h(c)=(f(c),g(c)). Это свойство универсальности и берется в качестве определения произведения объектов в произвольной категории.
· В категории
Set
произведение объектов
A
и В изоморфно их прямому (декартову) произведению как множеств.
 Доказательство:
с одной стороны мы определили h(c)=(f(c),g(c)). Докажем, что Доказательство:
с одной стороны мы определили h(c)=(f(c),g(c)). Докажем, что 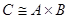 . .
Рассмотрим стрелку  . Очевидно, что l°h=1C
, h°l= . Очевидно, что l°h=1C
, h°l=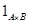 . Следовательно, . Следовательно, 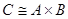 . .
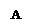
В категории Set копроизведение объектов А и В – это их дизъюнктное объединение А+В, т.е. объединение двух множеств, изоморфных А и В соответственно, но не пересекающихся. Точнее, пусть А’={<a,0>:aÎA}=A´{0} и B’={<b,1>:bÎB}=B´{1}. Положим А+В=A'ÈB’. инъекции iА
:А®А+В, iВ
:В®А+В определяются правилами iA
(a)=<a,0>, iB
(b)=<b,1> соответственно.
Данная категория состоит из одного объекта и одной стрелки. Этим она определяется полностью. Обозначим её единственный объект через а, а её единственную стрелку – через f. Так как в этой категории только один объект, то domf=codf=a, так как по определению категории с каждой стрелкой связано два объекта –её начало и конец. А в данном случае объект только один. У каждого объекта должна быть единичная стрелка. Но так как стрелка f – единственна, то её и берем в качестве единичной. Единственной парой, для которой нужно определить операцию композиции, является пара <f,f> и мы полагаем, что f°f=f. Это дает закон тождества, так как 1a
°f=f°1a
=f°f=f, и закон ассоциативности, так как f°(f°f)=(f°f)°f=f. Так мы определили категорию, которую можно изобразить так:

Эта категория имеет два объекта и три стрелки и выглядит так:
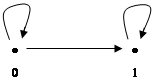 в качестве пары объектов возьмем числа 0 и 1, а в качестве стрелок – пары <0,0>, <0,1> и <1,1>. Пусть <0,0>:0®0, в качестве пары объектов возьмем числа 0 и 1, а в качестве стрелок – пары <0,0>, <0,1> и <1,1>. Пусть <0,0>:0®0,
<0,1>:0®1,
<1,1>:1®1.
Тогда <0,0>=10
(единичная стрелка на 0) и <1,1>=11
(единичная стрелка на 1). При наших требованиях к категориям, композицию на этом множестве можно ввести только одним способом: 10
°10
=10
, <0,1>°10
=<0,1>, 11
°<0,1>=<0,1>, 11
°11
=11
. тогда для любых объектов категории выполняется закон тождества и закон ассоциативности.
Эта категория имеет три объекта и шесть стрелок.
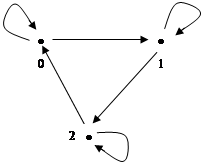 объекты: 0,1,2 объекты: 0,1,2
стрелки: <0,0>, <0,1>, <1,1>, <1,2>, <2,2>, <2,0>.
Стрелки <0,0>,<1,1>,<2,2> - единичные.
Композицию определяем следующим образом:
10
°10
=10
, 11
°11
=11
, 12
°12
=12
, <0,1>°10
=<0,1>, 11
°<0,1>=<0,1>, <1,2>°11
=<1,2>, 12
°<1,2>=<1,2>, <2,0>°12
=<2,0>, 10
°<2,0>=<2,0>. Тогда выполняется закон тождества и закон ассоциативности.
Категория, в которой любые два объекта p и q связаны не более чем одной стрелкой p®q, называется категорией предпорядка
. Если Р – совокупность объектов категории предпорядка, то на ней определено следующее бинарное отношение R: <p,q>ÎRÛ$ p®q. Отношение R обладает следующими свойствами:
2) рефлексивность
(вытекает из того, что для любого объекта категории существует единичная стрелка)
3) транзитивность
(вытекает из того, что стрелка p®q дает в композиции со стрелкой q®s стрелку p®s)
Первые три примера являются и примерами категории предпорядка. Но в них отношение предпорядка удовлетворяет еще свойству антисимметричности
, а именно если p®q и q®p, то p=q. Антисимметричное отношение предпорядка называют отношением частичного порядка. Простейшим примером категории предпорядка,  но не частичного порядка является двухобъектная категория с четырьмя стрелками: в этой категории существуют стрелки p→q и q→p, но р¹q. но не частичного порядка является двухобъектная категория с четырьмя стрелками: в этой категории существуют стрелки p→q и q→p, но р¹q.
Категория W называется дискретной, если в ней имеются только единичные стрелки, т.е. каждая стрелка является единичной для некоторого объекта. Отождествляя объекты с единичными стрелками, можно заметить, что дискретная категория есть не что иное, как совокупность объектов. Действительно, любое множество X можно превратить в дискретную категорию, добавив единичные стрелки для каждого xÎX.
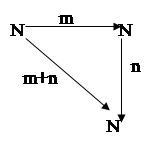 В этой категории ровно один объект, обозначаемый через N. Также категория имеет бесконечную совокупность стрелок из N в N. По определению этими стрелками являются натуральные числа 0,1,2,3… . Каждая стрелка имеет одно и то же начало и конец, а именно единственный объект N. Композиция двух стрелок (чисел) m и n есть снова число. Положим m°n=m+n. Итак, диаграмма коммутативна по определению. Закон ассоциативности для стрелок вытекает из ассоциативности сложения. В этой категории ровно один объект, обозначаемый через N. Также категория имеет бесконечную совокупность стрелок из N в N. По определению этими стрелками являются натуральные числа 0,1,2,3… . Каждая стрелка имеет одно и то же начало и конец, а именно единственный объект N. Композиция двух стрелок (чисел) m и n есть снова число. Положим m°n=m+n. Итак, диаграмма коммутативна по определению. Закон ассоциативности для стрелок вытекает из ассоциативности сложения.
 Единичная стрелка 1N
объекта N задается числом 0. Диаграмма коммутативна, так как 0+m=m n+0=n. Единичная стрелка 1N
объекта N задается числом 0. Диаграмма коммутативна, так как 0+m=m n+0=n.
1. Букур И., Деляну А. Введение в теорию категорий и функторов. – М.: Мир, 1972.
2. Голдблат Р. Топосы. Категорный анализ логики. – М.: Мир, 1983.
3. Скорняков Л.А. Элементы общей алгебры. – М.: Наука, 1983.
4. Цаленко М.Ш., Шульгейфер Е.Г. Основы теории категорий. – М.: Наука, 1974.
|