Лабораторная работа: Применение регрессионного анализа при оценке рисков
|
Название: Применение регрессионного анализа при оценке рисков Раздел: Рефераты по математике Тип: лабораторная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ГОУ ВПО ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ Отчет по лабораторной работе по дисциплине: "Оценка и анализ рисков" Исполнитель: Лебедева С.А. Факультет: Финансово-кредитный Специальность: Финансы и кредит Группа: 2 высшее, 5 курс № зачетной книжки 08ФФД62921 Руководитель: профессор Бутковский О.Я. Владимир 2010 ЗаданиеВ нижеприведенной таблице (Таблица 1) приведена информация по месячным доходностям за 2007г. индекса РТС и по пяти доходностям новых отраслей индексов российской торговой системы (РТС): нефть и газ (RTSog); электроэнергетика (RTSeu); телекоммуникации (RTStl); промышленность (RTSin); потребительские товары и розничная торговля (RTScr). Таблица 1
Требуется: Определить характеристики каждой ценной бумаги: α, β, рыночный (систематический) риск, собственный (несистематический) риск, R2 . Сформировать портфель минимального риска из двух видов отраслевых индексов RTStl и RTSog (при условии, что обеспечивается доходность портфеля (mp ) не менее, чем по безрисковым ценным бумагам (облигациям), - 0,5% с учетом общего индекса рынка. Построить линию рынка капитала (CML). Построить линию рынка ценных бумаг (SML). Решение . Для построения модели Марковица на первом этапе необходимо представить исходные данные в Excel в виде следующей таблицы.
Ввод исходных данных Применение регрессионного анализаПостроим модель зависимости доходности индекса телекоммуникации (RTStl) от индекса рынка. Параметры модели найдем с помощью инструмента Регрессия "Пакета анализа" Excel. Для проведения регрессионного анализа выполним следующие действия: Выбираем команду "Данные" → "Анализ данных". В диалоговом окне "Анализ данных" выбираем инструмент "Регрессия", а затем щелкаем по кнопке ОК. В диалоговом окне "Регрессия" в поле "Входной интервал Y" вводим адрес одного диапазона ячеек, который представляет зависимую переменную. В поле "Входной интервал X" вводим адрес диапазона, который содержит значения независимых переменных. Выбираем параметры вывода "новый рабочий лист" В поле "Остатки" проставляем необходимые флажки
Запуск анализа данных Результаты регрессионного анализаРезультаты регрессионного анализа содержатся в таб.2-4. Рассмотрим содержание этих таблиц. Во втором столбце таб.2 содержаться оценки параметров уравнения регрессии α и β. В третьем столбце содержаться стандартные ошибки коэффициентов уравнения регрессии, а в четвертом - t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии. Таблица 2
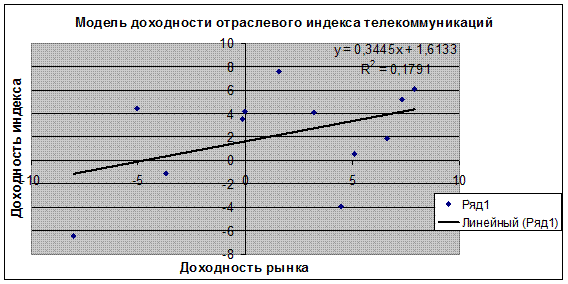
Уравнение регрессии зависимости доходности отраслевого индекса RTStl (m1 ) от индекса РТС (mr ) имеет вид: m1 =1,613+ 0,345* mr Таблица 3. Регрессионная статистика
Таблица 4. Дисперсионный анализ
Собственный (несистематический) риск отраслевого индекса RTStl (m1 ) равен σ2 ε1 =∑ε2 / (N-1) =158,067/11= 14,37 Аналогично построим модель зависимости доходности отраслевого индекса RTSog (m2 ) от индекса РТС (mr ), для этого выполним все вышеуказанные действия.
Заданы интервалы входных данных. В результате построения второй модели получаем следующие результаты: Таблица 5
Уравнение зависимости доходности отраслевого индекса RTSog (m2 ) от индекса РТС (mr ) имеет вид: m2 =-1,410+ 1,045* mr Таблица 6. Регрессионная статистика
Таблица 7. Дисперсионный анализ
Собственный (несистематический) риск отраслевого индекса RTStl (m1 ) равен σ2 ε2 =∑ε2 / (N-1) = 81,799/11=7,44, R2 =0,50 Решение оптимизационной задачиНеобходимо найти вектор Х= (х1 , х2 ), минимизирующий риск портфеля σр . Решение задачи можно получить в среде Excel с помощью надстройки "Поиск решения". Экономико-математическая модель задачиХ1 - доля в портфеле отраслевого индекса RTStl Х2 - доля в портфеле отраслевого индекса RTSog В нашей задаче задана эффективность портфеля не ниже, чем в среднем по облигациям, то есть 0,5% в месяц. σр =√ (∑хi βi ) 2 σ2 mr +∑хi σ2 εi = =√ (0,3452 х1 2 +2*1,045*0,345*х1 *х2 +1,0452 х2 2 ) *5,142 +14,37х1 2 +7,44 х2 2 => => min; х1 +х2 =1 mp =∑ хi (αi +βi mr ) =x1 (1,613+0,345*1,59) + x2 (-1,410+1,045*1,59) ≥0,5; х1 ; х2 ≥0 Последовательность решения оптимизационной задачи в среде Excel представлена.
Подготовлена форма для ввода данных.
Введение исходных данных. (в ячейках D5 и Е5 (эти ячейки называются изменяемыми) будут находиться значения неизвестных Х1 и Х2 )
Ввод формулы. (для ввода формулы для расчета целевой функции воспользуемся функцией КОРЕНЬ (шаг 1) )
Введение подкоренного выражения (шаг 2.)
Введение левой части системы ограничений по доходности портфеля.
Введение левой части системы ограничений по долям бумаг.
Указание целевой ячейки (НЗ), изменяемых ячеек ( D6: 5Е)
Добавление ограничений.
Указание параметров.
Решение найдено. Ответ. Минимальный риск портфеля, равный 3,96%, будет достигнут, если доля отраслевого индекса телекоммуникаций (RTStl) составит77,02%, а доля отраслевого индекса нефти и газа (RTSog) - 22,98%. Полученные результаты можно представить в графическом виде, используя линию рынка ценных бумаг.
Зависимость индекса телекоммуникаций от общего индекса рынка: RTStl (телекоммуникации); - связь с рынком.
Зависимость индекса нефти и газа от общего индекса рынка: RTSog (нефть и газ); -связь с рынком Приложение
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||