| Ряды динамики. Классификация динамических рядов
Ряд динамики, хронологический ряд, динамический ряд, временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Всякий ряд динамики включает, следовательно, два обязательных элемента: во-первых, время и, во-вторых, конкретное значение показателя, или уровень ряда. Ряды динамики различаются по следующим признакам.
1. По времени
– моментные и интервальные ряды. Интервальный ряд динамики
– последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам и т.д. Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики.
Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода и т.д. Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда дает вполне реальный показатель – общий выпуск продукции за год, общие затраты рабочего времени, общий объем продаж акций и т.д., сумма же уровней моментного ряда, хотя иногда и подсчитывается, но реального содержания, как правило, не имеет.
2. По форме представления уровней –
ряды абсолютных, относительных и средних величин (табл. 6.1 – 6.3).
3. По расстоянию между датами или интервалам времени
выделяют полные и неполные хронологические ряды.
Полные ряды динамики
имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Это равноотстоящие ряды динамики (см. табл. 6.1 и 6.2). Неполные
– когда принцип равных интервалов не соблюдается (см. табл. 6.3).
Таблица 6.1
Объем продаж долларов США на ММВБ, млн. долл.
| Дата
|
10.01.94
|
11.01.94
|
12.01.94
|
13.01.94
|
| Объем продаж
|
126,750
|
124,300
|
148,800
|
141,400
|
Таблица 6.2
Индекс инфляции в 1993 г. (на конец периода, в % к декабрю 1992 г.)
| Период
|
Январь
|
Февраль
|
Март
|
Апрель
|
Май
|
Июнь
|
| Индекс инфляции
|
126
|
162
|
190
|
221
|
264
|
310
|
Таблица 6.3
Потребление основных продуктов питания на одного члена семьи, кг/год
| Продукты
|
1980
|
1985
|
1990
|
1991
|
1992
|
1993
|
| Мясо и мясопродукты
|
80,0
|
78,4
|
74,1
|
68,3
|
58,7
|
63,2
|
| Молоко и молочные продукты
|
411,2
|
389,6
|
378,9
|
345,4
|
280,4
|
285,6
|
| Хлебные продукты
|
101,2
|
91,6
|
85,7
|
91,8
|
98,0
|
105,81
|
Чтобы о развитии явления можно было получить представление при помощи числовых уровней, при составлении ряда динамики должны приводиться в сопоставительный вид.
Статистические данные должны быть сопоставимы
по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории
означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов
означает сравнение совокупностей с равным числом элементов. Территориальная и объемная сопоставимость обеспечивается смыканием рядов динамики, при этом либо абсолютные уровни заменяются относительными, либо делается пересчет в условные абсолютные уровни. Не возникает особых сложностей при обеспечении сопоставимости
данных по единицам измерения; стоимостная сравнимость
достигается системой сопоставимых цен.
Числовые уровни рядов динамики должны быть упорядоченными во времени.
Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.
6.2. Показатели анализа рядов динамики
При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут:
1) абсолютный прирост,
2) темпы роста,
3) темпы прироста,
4) абсолютное значение одного процента прироста.
Расчет показателей динамики представлен в следующей таблице.
| Показатель
|
Базисный
|
Цепной
|
| Абсолютный прирост 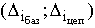 * *
|
Yi
-Y0
|
Yi
-Yi-1
|
| Коэффициент роста (Кр
)
|
Yi
: Y0
|
Yi
: Yi-1
|
| Темп роста (Тр
)
|
(Yi
: Y0
)×100
|
(Yi
: Yi-1
)×100
|
| Коэффициент прироста (Кпр
)**
|
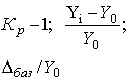
|
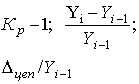
|
| Темп прироста (Тпр
)
|
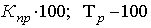
|
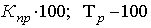
|
| Абсолютное значение одного процента прироста (А)
|
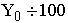
|
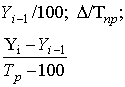
|
*
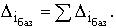
**
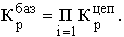
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели.
Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.
Рассмотрим пример. Имеются данные об объемах и динамике продаж акций на 15 крупнейших биржах России за пять месяцев 1993 г.
| Показатель
|
Март
|
Апрель
|
Май
|
Июнь
|
Июль
|
Август
|
| Объем продаж, млн. руб.
Абсолютный прирост:
цепной,
базисный
Коэффицент (индекс) роста цепной
Темп роста, %:
цепной,
базисный
Темп прироста
цепной, %
базисный, %
Абсолютное значение 1% прироста (цепной)
|
709,98
-
-
-
-
100
-
-
-
|
1602,61
892,63
892,63
2,257
225,7
225,7
125,7
125,7
7,10
|
651,83
-950,78
-58,15
0,407
40,7
91,8
-59,3
-8,2
16,03
|
220,80
-431,03
-489,18
0,339
33,9
31,1
-66,1
-68,9
6,52
|
327,68
106,88
-382,3
1,484
148,4
46,2
48,4
-53,8
2,21
|
277,12
-50,56
-432,86
0,846
84,6
39,0
-15,4
61,0
3,28
|
Система средних показателей динамики включает:
средний уровень ряда,
средний абсолютный прирост,
средний темп роста,
средний темп прироста.
Средний уровень ряда –
это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.
Для интервальных рядов с равными периодами времени средний уровень Y рассчитывается следующим образом:
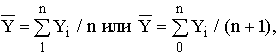
где n или (n +1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Yi
(1 = 1, 2, ..., n или 1 = 0, 1, 2, ..., n).
Средний абсолютный прирост
рассчитывается по формулам в зависимости от способа нумерации интервалов (моментов).
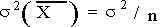 . .
Средний темп роста:
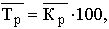
где 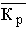 – средний коэффициент роста, рассчитанный как – средний коэффициент роста, рассчитанный как 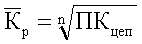 . Здесь Кцеп
– цепные коэффициенты роста; . Здесь Кцеп
– цепные коэффициенты роста;
Средний темп прироста
(%) определяется по единственной методологии:
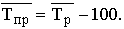
6.3. Изучение тенденции развития
Всякий ряд динамики теоретически может быть представлен в виде составляющих:
1) тренд – основная тенденция развития динамического ряда (к увеличению либо снижению его уровней);
2) циклические (периодические) колебания, в том числе сезонные;
3) случайные колебания.
Изучение тренда включает два основных этапа:
1) ряд динамики проверяется на наличие тренда;
2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Непосредственное выделение тренда
может быть произведено тремя методами.
1. Укрупнение интервалов.
Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).
2. Скользящая средняя.
В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек).
При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %.
Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной.
3. Аналитическое выравнивание.
Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели
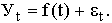
где f(t) – уровень, определяемый тенденцией развития;
et
– случайное и циклическое отклонение от тенденции.
Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
Чаще всего при выравнивании используются следующие зависимости:
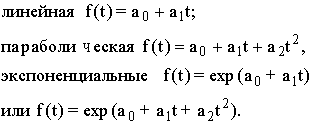
Линейная зависимость
выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость
используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости
применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.п.).
Оценка параметров (a0
, a1
, a2
, ...) осуществляется следующими методами:
1) методом избранных точек,
2) методом наименьших расстояний,
3) методом наименьших квадратов (МНК).
В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:
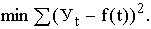
Для линейной зависимости (f(t)=a0
+a1
t) параметр а0
обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а1
– сила связи, т.е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а можно представить как постоянный теоретический абсолютный прирост. Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (Fфакт
) сравнивается с теоретическим (табличным) значением:
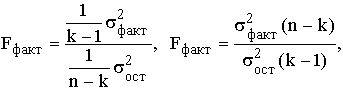
где k – число параметров функции, описывающей тенденцию;
n – число уровней ряда;
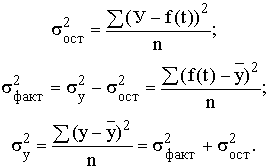
Fфакт
сравнивается с Fтеор
при v1
= (k-1), v2
= (n-k) степенях свободы и уровне значимости a (обычно a = 0,05). Если Fфакт
> Fтеор
, уравнение регрессии значимо, т.е. построенная модель адекватна фактической временной тенденции.
Выравнивание проведено по линейной трендовой модели. Оценка параметров уравнения выполнена методом наименьших квадратов.
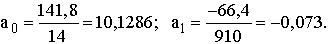
Таким образом, f(t) = уt
= 10,128-0,073t для t= -13, -11, -9, ..., +13, или f(t) = уt
= 11,077-0,1461 для t = 0, 1, ..., 13.
Параметры последнего уравнения регрессии можно интерпретировать следующим образом: a0
= 11,077 – это исходный уровень брачности по России за период до 1977 г.; а1
= -0,146 – показатель силы связи, т.е. в России за период с 1977 по 1990 г. происходило снижение уровня брачности на 0,146 ‰ ежегодно.
В качестве примера рассмотрим число зарегистрированных браков на 1000 жителей России за период с 1977 по 1990 г.:
Год
|
Число зарегистри-
рованных браков, %
|
t
|
у×t
|
t2
|
f(t)
|
| 1977
|
11,2
|
-13
|
-145,6
|
169
|
11,077
|
| 1978
|
10,9
|
-11
|
-119,9
|
121
|
10,931
|
| 1979
|
10,7
|
-9
|
-96,3
|
81
|
10,785
|
| 1980
|
10,6
|
-7
|
-74,2
|
49
|
10,639
|
| 1981
|
10,6
|
-5
|
-53,2
|
25
|
10,493
|
| 1982
|
10,4
|
-3
|
-31,2
|
9
|
10,347
|
| 1983
|
10,4
|
-1
|
-10,4
|
1
|
10,202
|
| 1984
|
9,6
|
1
|
9,6
|
1
|
10,056
|
| 1985
|
9,7
|
3
|
29,1
|
9
|
9,910
|
| 1986
|
9,8
|
5
|
49,0
|
25
|
9,764
|
| 1987
|
9,9
|
7
|
69,3
|
49
|
9,618
|
| 1988
|
9,5
|
9
|
85,5
|
81
|
9,472
|
| 1989
|
9,4
|
11
|
103,4
|
121
|
9,326
|
| 1990
|
9,1
|
13
|
118,3
|
169
|
9,180
|
| Итого
|
141,8
|
0
|
-66,4
|
910
|
141,800
|
Следующий шаг аналитического выравнивания – оценка надежности уравнения регрессии:
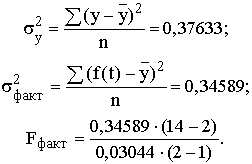
Таким образом, Fтеор
= 4,747; a = 0,05; v1
(k-
1) = 1; v2
= (n-k) = 12 и Fтеор
= 9,330 при a = 0,01, v1
= 1, v2
= 12.
Fфакт
> Fтеор
, и уравнение прямой адекватно отражает сложившуюся в исследуемом ряду динамики тенденцию.
|