1. Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность ого, что изделию первого вида будет присвоен знак качества, равна 0,7; для изделия второго вида эта вероятность равна 0,9; а для изделия третьего вида 0,8. Найти вероятность того, что знак качества будет присвоен: а) всем изделиям; б) только одному изделию; в) хотя бы одному изделию
РЕШЕНИЕ
Испытание: знак качества будет присвоен всем изделиям.
   Событие: А=07 – присвоен первому изделию, Р(В)=0,9 – присвоен второму изделию, Р(С)=0,8 – присвоен третьему изделию; тогда Р(А)=0,3; Р(В)=0,1; Р(С)=0,2. Событие: А=07 – присвоен первому изделию, Р(В)=0,9 – присвоен второму изделию, Р(С)=0,8 – присвоен третьему изделию; тогда Р(А)=0,3; Р(В)=0,1; Р(С)=0,2.
а) Рвсем изделиям
= Р(А)*Р(В)*Р(С)
Рвсем изделиям
=0,7*0,9*0,8=0,504.
      в) Ртолько одному
=Р(А,В,С или А,В,С или А,В,С) в) Ртолько одному
=Р(А,В,С или А,В,С или А,В,С)
Ртолько
.одному
=0,7*0,1*0,2+0,3*0,9*0,2+
+0,3*0,1*0,8=0,014+0,054+0,024=0,092
   с) Рхотя бы одному
=1 - Рни одному
=1-Р(А)*Р(В)*Р(С) с) Рхотя бы одному
=1 - Рни одному
=1-Р(А)*Р(В)*Р(С)
Рхотя бы одному
=1-0,3*0,1*0,2=1-0,006=0,994.
11. Оптовая база снабжает товаром 9 магазинов. Вероятность того, что в течение дня поступит заявка на товар, равна 0,5 для каждого магазина. Найти вероятность того, что в течение дня а) поступит 6 заявок, б) не менее 5 и не более 7 заявок, в) поступит хотя бы одна заявка. Каково наивероятнейшее число поступающих в течение дня заявок и чему равна соответствующая ему вероятность.
РЕШЕНИЕ
Обозначим событие А – поступила заявка
По условию р=Р(А)=0,5
q=P(A)=1-0,5=0,5
n= 9 к=6
а) Так как число повторных испытаний n= 9, применим формулу Бернулли.
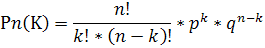
Р9(6)= * *
б) К1=5, К2=7
Р9(5≤m≤7)=P9
(5)+P9
(6)+P9
(7)
Р9(5)= * *
Р9(7)= * *
Р9(5≤m≤7)=0.246+0.0702+0.16=0.4762
в) Рn
(событие наступит хотя бы 1 раз)=1-qn
Р9
=1-0,59
=1-0,001953=0,998
г) np-q≤K0
≤np+p
9*0.5-0.5≤K0
≤9*0.5+0.5
4≤K0
≤5 K0
=5
K9
(5)= *0.55
*0.59-5
= *0.55
*0.59-5
=
Ответ: а) 0,16 б) 0,4762 в) 0,998 г) K0
=5 Р(K0
)=0,246.
21. Найти: а) математическое ожидание, б) дисперсию, в) среднее квадратическое отклонение дискретной случайной величины Х по известному закону ее распределения, заданному таблично:
| Х |
8 |
4 |
6 |
5 |
| Р |
0,2 |
0,5 |
0,2 |
0,1 |
Решение
а) Найдем математическое ожидание Х:
М(Х)=8*0,2+4*0,5+6*0,2+5*0,1=5,3.
б) Для нахождения дисперсии запишем закон распределения Х2
:
| Х2
|
64 |
16 |
36 |
25 |
| Р |
0,2 |
0,5 |
0,2 |
0,1 |
Найдем математическое ожидание Х2
:
М(Х2
)=64*0,2+16*0,5+36*0,2+25*0,1=30,5
Найдем искомую дисперсию:
D(X)=M(X2
)-[M(X)]2
D(X)=30.5-(5.3)2
=2.41
в) найдем искомое среднее квадратическое отклонение:

Ответ: а) 5,3 б) 2,41 в) 1,55
31. Случайная величина Х интегральной функцией распределения F(Х).
Требуется: а) найти дифференциальную функцию распределения (плотность вероятности) б) найти математическое ожидание и дисперсию Х в) построить графики интегральной и дифференциальной функций распределения.

F(X
Решение:

а)  = F(X = F(X
б) М(х)= . .
М(х2
)= . .
D(x)=M(x2
)-[M(x)]2
=2-

в) построить графики функций F(x) и f(x):
 
41. Заданы математическое ожидание а=15 и среднее квадратичное отклонение б=2 нормально распределенной величины Х. Требуется найти: а) вероятность того, что Х примет значение, принадлежащие интервалу (9; 19). б) вероятность того, что абсолютная величина отклонения «Х-а» окажется меньше δ=3
Решение
а) воспользуемся формулой:

по условию задачи α=9 β=19 а=15 б=2 следовательно,

По таблице приложения 2:  0,4772; 0,4772; 
Искомая вероятность попадания нормально распределенной случайной величины в интервал (9; 19) равна:
 0,4772+0,49865=0,976065 0,4772+0,49865=0,976065
б) вероятность того, что абсолютная величина отклонения «Х-а» окажется меньше δ=3, равна
Р(
Р(|х-а|<3)=2*Ф(3/2)=2*0,4332=0,8664.
Ответ: а) 0,976065; б) Р(|х-а|<3)= 0,8664. 0,976065; б) Р(|х-а|<3)= 0,8664.
51. Даны выборочные варианты х1
и соответствующие им частоты ni
количественного признака Х. а) найти выборочные среднюю дисперсию и среднеквадратическое отклонение. б) Считая, что количественный признак Х распределен по нормальному закону и что выборочная дисперсия равна генеральной дисперсии, найти доверительный интервал для оценки математического ожидания с надежностью γ=0,99
| хi
|
10,2 |
15,2 |
20,2 |
25,2 |
30,2 |
35,2 |
40,2 |
| ni
|
3 |
15 |
26 |
54 |
12 |
5 |
3 |
Решение
1. Объем выборки
n=
Средняя выборочная:
 = =
Выборочная дисперсия:
Dв
= 2
– 2
–  2
, где 2
, где  =23,76 =23,76
Средняя выборочная квадратов значений признака γ
 = =
Тогда Dв
=598,87-(23,76)2
=34,33
Среднее квадратичное отклонение:
σв
= σв
= σв
= 5,86 5,86
пусть количественный признак Х генеральной совокупности распределен по нормальному закону, причем среднеквадратическое значение отклонение «σ» этого распределения известно. Тогда с вероятностью γ доверительный интервал заданный формулой
 ; ;  ), ),
покрывает неизвестное математическое ожидание. Здесь число t находится из соотношения 2Ф(t)=γ с помощью таблицы интегральной функции Лапласса.
В данной задаче γ=0,99, поэтому 2Ф(t)=0,99, а Ф(t)=0,495, по таблице находим t=2,58.
По условию задачи дисперсия генеральной совокупности D=Dв
и, следовательно, σ=σв
=5,86. ранее найдены значения n=118, и Хв
=23,76. Поэтому можно найти доверительный интервал:

(23,76-1,39; 23,76+1,39)
(22,37; 25,15).
Ответ: Хв
=23,76; Dв
=34,33; σв
=5,86; а (22,37; 25,15). (22,37; 25,15).
61. По данным корреляционной таблицы найти условные средние Yx
и Xy
. Оценить тесноту линейной связи между признаками X и Y и составить уравнение линейной регрессии Y по X и X по Y. Сделать чертеж, нанеся на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
| Y\X |
5 |
10 |
15 |
20 |
25 |
30 |
Ny
|
| 35 |
4 |
2 |
6 |
| 45 |
5 |
3 |
8 |
| 55 |
5 |
45 |
5 |
55 |
| 65 |
2 |
8 |
7 |
17 |
| 75 |
4 |
7 |
3 |
14 |
| Nx
|
4 |
7 |
10 |
57 |
19 |
3 |
n=100 |
Найдем условные средние воспользовавшись формулами:
Үx
= Xy
= Xy
=
Yx
=5
= Xy
=35
= Xy
=35
=
Yx
=10
= Xy
=45
= Xy
=45
=
Yx
=15
= Xy
=55
= Xy
=55
=
Yx
=20
= Xy
=65
= Xy
=65
=
Yx
=25
 Xy
=75
= Xy
=75
=
Yx
=30

Оценка тесноты линейной связи между признаками X и Y производится с помощью коэффициента линейной корреляции r:

Коэффициент r может принимать значения от -1 до +1.
Знак r указывает на вид связи: прямая или обратная. Абсолютная величина |r| на тесноту связи. При r>0 связь прямая, то есть с ростом х растет у.
При r<0 связь обратная, то есть с ростом х убывает у.
Для нахождения rвычислим указанные общие средние: х, у, ху, а также средние квадратические отклонения σх
и σу
. Вычисления удобно поместить в таблицах, куда вписываем также найденные ранее условные средние.
Значение коэффициента линейной корреляции
| Х |
nx
|
x*nx
|
x2
*nx
|
 yx yx
|
 x*nx
*yx x*nx
*yx
|
| 5 |
4 |
20 |
100 |
35 |
700 |
| 10 |
7 |
70 |
700 |
42.14 |
2949.8 |
| 15 |
10 |
150 |
2250 |
54 |
8100 |
| 20 |
57 |
1140 |
22800 |
57.8 |
65892 |
| 25 |
19 |
475 |
11875 |
66.05 |
31373.75 |
| 30 |
3 |
90 |
2700 |
75 |
6750 |
 |
100 |
1945 |
40425 |
- |
115765.55 |
| Y |
ny
|
y*ny
|
y2
*ny
|
 xy xy
|
 y*ny
*xy y*ny
*xy
|
| 35 |
6 |
210 |
7350 |
6.67 |
1400.7 |
| 45 |
8 |
360 |
16200 |
11.875 |
4275 |
| 55 |
55 |
3025 |
166375 |
20 |
60500 |
| 65 |
17 |
1105 |
71825 |
21.47 |
23724.35 |
| 75 |
14 |
1050 |
78750 |
24.64 |
25872 |
 |
100 |
5750 |
340500 |
- |
115772.05 |
С помощью таблиц находим общие средние, средние квадратов, среднюю произведения и среднеквадратические отклонения:
Х=
X2
= 5 5
XY=
Y= 57.5 57.5
Y2
=
 σx
= σx
= = = = =
 σy
= σy
= = = =9.94 =9.94
Отсюда коэффициент корреляции равен:
r=
т.к r > 0, то связь прямая, то есть с ростом Х растет Y.
т.к | r | > 0,78 то линейная связь высокая.
Находим линейное уравнение регрессии Y по X:

Yx
-57.5=0.78*
Yx
=1.52x+27.94
Аналогично находим уравнение регрессии X поY:

Xy
-19.45=0.78*
Xy
=0.4y-3.55
Данные уравнения устанавливают связь между признаками X и Y и позволяют найти среднее значение признака Yx
для каждого значения x и аналогично среднее значение признака Xy
для каждого значения y.
Изобразим полученные результаты графически.
  Нанесем на график точки (х;ух
) отметив их звездочками( ). Нанесем на график точки (ху
;у) отметив их кружочками ( ). Построим каждое из найденных уравнений регрессии по двум точкам: Нанесем на график точки (х;ух
) отметив их звездочками( ). Нанесем на график точки (ху
;у) отметив их кружочками ( ). Построим каждое из найденных уравнений регрессии по двум точкам:
Yx
=1.52x+27.94
 Xy
=0.4y-3.55 Xy
=0.4y-3.55
Обе прямые регрессии пересекаются в точке (х;у). В нашей задаче это точки (19,45; 57,5).
Оценка тесноты любой связи между признаками производится с помощью корреляционных отношений Y по X и X по Y:
ηух
=
Дисперсия  называемые внутригрупповыми, определены ранее. называемые внутригрупповыми, определены ранее.
Величины  называются межгрупповыми дисперсиями и вычисляются по формулам: называются межгрупповыми дисперсиями и вычисляются по формулам:
    
Они характеризуют разброс условных средних, от общей средней. В данной задаче:


бх
=
бу
=
Тогда корреляционные отношения равны:
ηух
=
ηху
=
Ответ: Корреляционная связь между признаками высокая ее можно описать уравнениями:
Yx
=1.52x+27.94,
Xy
=0.4y-3.55.
|