Контрольная работа
«Методы оптимизации
при решении уравнений
»
Задание №1
Определить, существует ли кривая 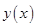 , доставляющая функционалу экстремум и, если существует, то найти ее уравнение. , доставляющая функционалу экстремум и, если существует, то найти ее уравнение.
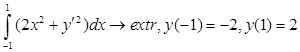
Решение:
Составим уравнение Эйлера и найдём его общее решение:
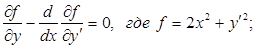
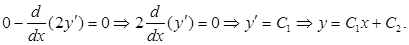
Используем краевые условия:
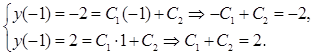
Решаем систему уравнений и получаем:
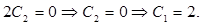
Таким образом, экстремаль имеет уравнение вида
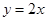
Так как
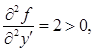
то функционал на прямой 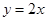 достигает минимума. достигает минимума.
Задание №2
Найти, используя уравнение Эйлера-Лагранжа, оптимальное управление 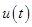 , минимизирующее функционал , минимизирующее функционал 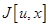 для системы, описываемой уравнениями для системы, описываемой уравнениями
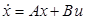 , ,
при начальных и конечных условиях соответственно:
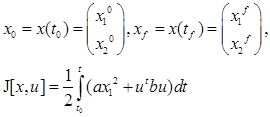
| A |
B |
t0
|
tf
|
x0
|
xf
|
a |
b |
0 1
0 0
|
0
1
|
0 |
1 |
1
0
|
0
0
|
0 |
1 |
Решение
Формируем задачу по исходным данным:
 (1) (1)
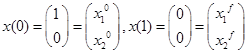 (2) (2)
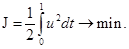
Составим функцию Лагранжа и гамильтониан:
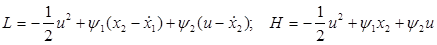
и соответственно уравнения Эйлера-Лагранжа (здесь для Н):
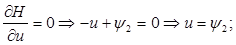 (3) (3)
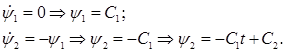 (4) (4)
Используя замену (3), подставим выражения (4) во второе уравнение динамики в (1):
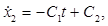 
и находим общее решение
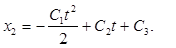 (5) (5)
Подставим его в первое уравнение (1):
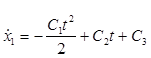
и находим общее решение:
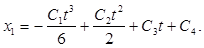 (6) (6)
Для 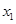 из (6) и из (6) и 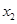 из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1
, С2
, С3
, С4
,: из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1
, С2
, С3
, С4
,:
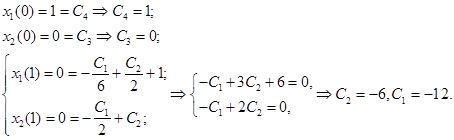
Таким образом, решение имеет вид:
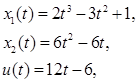
которое удовлетворяет начальным и конечным условиям.
Задание №3
Для системы, описываемой уравнениями
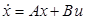
с заданными условиями на начальное 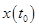 и конечное и конечное 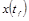 значение координат, найти оптимальное управление значение координат, найти оптимальное управление 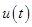 , минимизирующее функционал , минимизирующее функционал
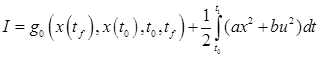
| A |
B |
t0
|
tf
|
x0
|
xf
|
g0
|
a |
b |
0 1
0 0
|
0
1
|
0 |
t |
1
0
|
x1
(tf
) = -tf
2
|
0 |
0 |
1 |
Решение.
Формулируем задачу по исходным данным
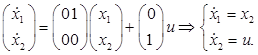 (1) (1)
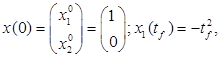 (2) (2)
т.е. 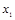 ,подвижна на правом конце, координата ,подвижна на правом конце, координата 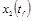 - свободна на правом конце, - свободна на правом конце,
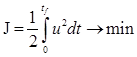
Составим функцию Гамильтона Н (или функцию Лагранжа L)
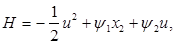 (3) (3)
и соответствующие уравнения Эйлера-Лагранжа:
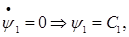 (4) (4)
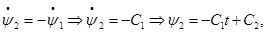 (5) (5)
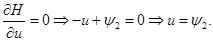 (6) (6)
Составим вспомогательную функцию
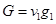 , ,
где 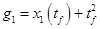 .Таким образом: .Таким образом:
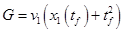 . (7) . (7)
Поскольку 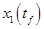 и и 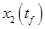 подвижны, то используем условия трансверсальности: подвижны, то используем условия трансверсальности:
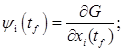
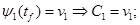 (8) (8)
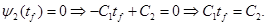 (9) (9)
Так как не фиксирован момент времени 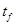 , то используем условие трансверсальности , то используем условие трансверсальности
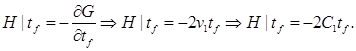
Найдем значение 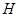 при при 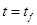 из (3), но учтем, что из (3), но учтем, что  , а , а 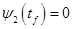 из (9). Тогда, учитывая (4): из (9). Тогда, учитывая (4):
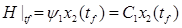
и используя (10) получим:
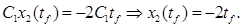 (11) (11)
Подставляя (4), (5) и (6) в (2), а потом в (1) и интегрируя получим:
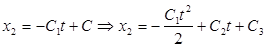 (12), (12),
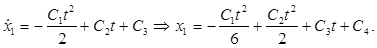 (13) (13)
Используя начальные условия, можем записать:
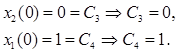
Запишем условие 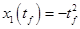 с учетом (13). Тогда: с учетом (13). Тогда:
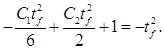 (14) (14)
Уравнения (9), (11) и (14) составляют систему уравнений с тремя неизвестными С1
, С2
и 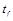 : :
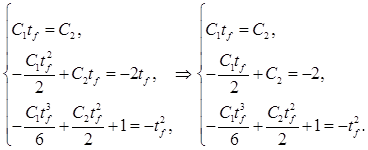
Подставляя 1-е уравнение во 2-е, получим:
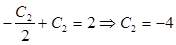 , ,
а подставляя 1-е в третье, получим:
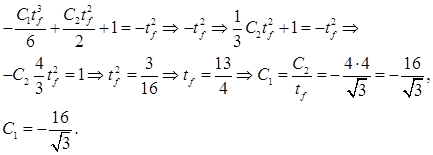
Таким образом, решение имеет вид:
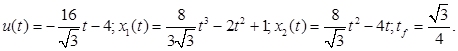
Задание №4
Используя метод динамического программирования найти оптимальное уравнение для системы
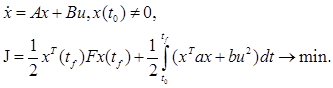
| A |
B |
t0
|
tf
|
F |
a |
b |
0 1
0 0
|
0
1
|
0 |
∞ |
0 |
1 0
0 2
|
1 |
Решение:
Формируем задачу по исходным данным.
 (1) (1)
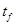 – не ограничено, то есть – не ограничено, то есть 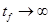 . .
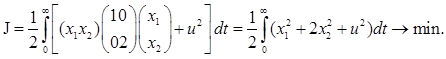
Составим уравнение Беллмана с учетом того, что 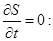 (S-функция Беллмана) (S-функция Беллмана)
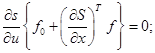 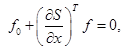 (2) (2)
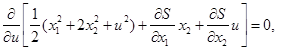 (3) (3)
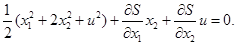 (4) (4)
Из (3) находим:
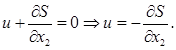 (5) (5)
Подставим (5) в (4)
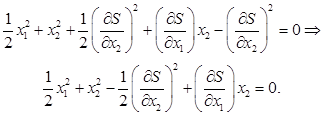 (6) (6)
Представим функцию Беллмана в виде квадратичной формы
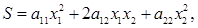 (7) (7)
причем это должна быть положительно определенная квадратичная форма, а значит
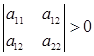 (8) (8)
т.е. матрица должна быть положительно определённой.
Вычисляя выражения:
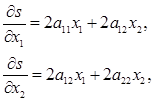 (9) (9)
подставим их в (6) и обратим коэффициенты при 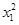 , , 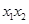 и и 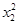 в ноль, т.к. справа у нас ноль: в ноль, т.к. справа у нас ноль:
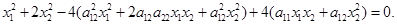
Отсюда:
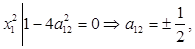 (10) (10)
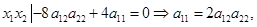 (11) (11)
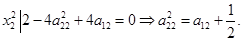 (12) (12)
Если 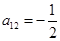 , то , то 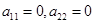 Þ S < 0, что нельзя допустить. Тогда: Þ S < 0, что нельзя допустить. Тогда:
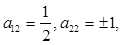
а следовательно а12
и а22
должны быть одного знака, так как а11
> 0.
Тогда а12
= 1/2, а22
= 1, а11
= 1. Таким образом, решение имеет вид (из (5) и (9)):
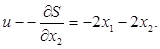
Задача 5
Используя принцип максимума Понтрягина найти оптимальное управление для линейной системы
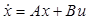
в задаче:
| А |
В |
t0
|
tf
|
х0
|
xf
|
|u| |
0 1 0
0 0 1
0 0 0
|
0
0
1
|
0 |
1 |
0
0
0
|
x1
®max
0
0
|
£1 |
Решение:
Формируем задачу по исходным данным:
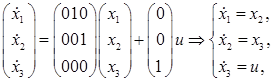
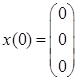 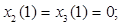 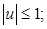
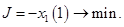 (4) (4)
Составим функцию Гамильтона
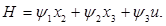
Уравнения Эйлера-Лагранжа имеет вид:
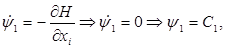 (5) (5)
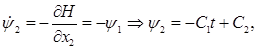 (6) (6)
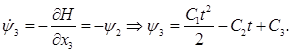 (7) (7)
Поскольку 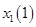 – подвижна, то используем условие трансверсальности: – подвижна, то используем условие трансверсальности:
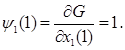
Но из (5) видно, что y1
= С1
Þ С1
= 1. Тогда из (7) видно, что y3
= t2
/2-C2
t+C3
, - то есть это квадратичная парабола ветвями вверх, которая может дважды пересечь уровень y3
= 0 и возможных порядок следования интервалов знакопостоянства следующий: +, -, +.
Из принципа максимума следует:
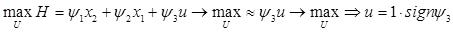 , ,
а следовательно:
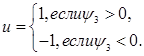
Тогда, поскольку y3
меняет знак дважды, (пусть в моменты t1
и t2
) можем записать
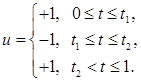 (8) (8)
Подставим 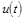 в (3) и получим, проинтегрировав уравнение (3) в (3) и получим, проинтегрировав уравнение (3)
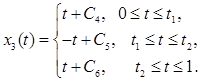 (9) (9)
Используя начальные и конечные условия для х3
и условия непрерывности 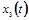 в t1
и t2
получим: в t1
и t2
получим:
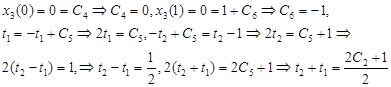 (10) (10)
Подставим (9) и константы из (10) в (2) и проинтегрируем. Получим:
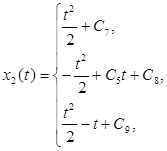 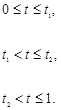 (11) (11)
Используя начальные и конечные условия для х2
и условия непрерывности в t1
и t2
, получим:
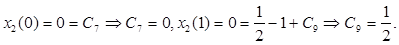
Используем непрерывность 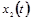 при при  и и 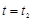 : :
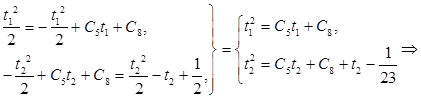
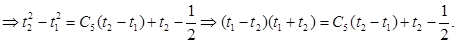
Собрав уравнения (10) и полученное уравнение составим систему уравнений:
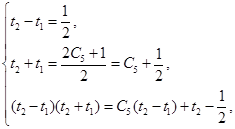 (12-14) (12-14)
Подставив (12) в (13), получим уравнение
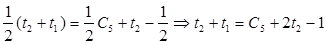 . .
Подставим (13) в полученное уравнение (вместо 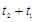 ): ):
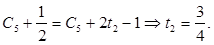
Тогда t1
из (12) равно
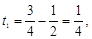
и, наконец,
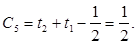
Подставим (11), с учетом найденных констант в (1):
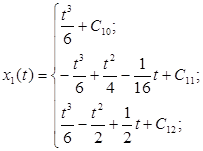 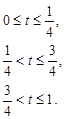 (15) (15)
Исходя из начального условия и условия непрерывности получим:
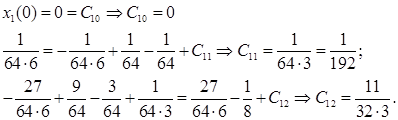
Таким образом: моменты переключения: t1
=1/4, t2
=3/4, а 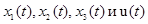 заданы уравнениями(15), (11), (9) и (8) с известными константами. заданы уравнениями(15), (11), (9) и (8) с известными константами.
Задание №6
Установить управляемость и наблюдаемость линейной системы:
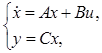
где
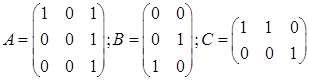 . .
Решение:
Для оценки управляемости составим матрицу управляемости (учтем, что n=3);
Y = (B, AB, A2
B):
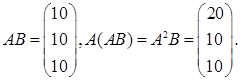
Таким образом

Взяв минор из 1,2 и 3 столбцов можно видеть, что
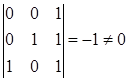 . .
Следовательно, rang(Y)=3=n и система вполне управляема.
Для оценки наблюдаемости системы составим матрицу наблюдаемости (n=3):
H=(CT
, AT
CT
, (AT
)2
CT
);
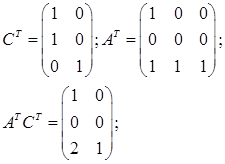
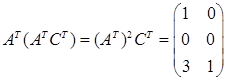 . .
Таким образом

Взяв минор из 1, 2 и 3 столбцов можно видеть, что
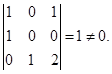
Таким образом rang(H) = 3 = n, а следовательно система вполне наблюдаема.
Задание №7
Для линейной системы 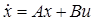 и квадратичного критерия и квадратичного критерия
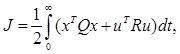
выполнить синтез оптимального управления с обратной связью
| A |
B |
Q |
R |
0 1
1 0
|
1
0
|
1 0
0 0
|
1 |
Решение:
Требуется выполнить синтез стационарного регулятора. Для этого воспользоваться алгебраическим матричным уравнением Риккати:
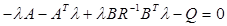
где
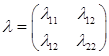 , ,
причем матрица l>0 (положительно определена).
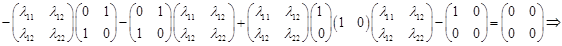 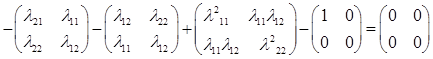
Сравнивая коэффициенты матрицы слева и справа, стоящих на одинаковых местах получим систему уравнений:
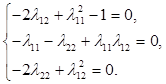
Решая систему уравнений с учетом положительной определенности матрицы l, получим:
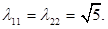 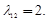
Тогда для уравнения, которое имеет вид
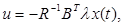
получим:
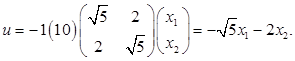
|