Башкирский Государственный Аграрный Университет
Факультет: экономический
Кафедра: статистики и информационных систем в экономике
Специальность: бухгалтерский учет, анализ и аудит
Форма обучения: заочная
Курс, группа: III, 4
Контрольная работа
Эконометрика
Уфа 2009
Введение
Эконометрика – наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов..
Этапами эконометрических исследований являются:
- постановка проблемы;
- получение данных, анализ их качества;
- спецификация модели;
- оценка параметров;
- интерпретация результатов.
Эконометрическое исследование включает решение следующих проблем:
- качественный анализ связей экономических переменных – выделение зависимых и независимых переменных;
- подбор данных;
- спецификация формы связи между у и х;
- оценка параметров модели;
- проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты;
- анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, выявление переменных, ответственных за мультиколлинеарность;
- введение фиктивных переменных;
- выявление автокорреляции, лагов;
- выявление тренда, циклической и случайной компонент;
- проверка остатков на гетероскедатичность;
- и др.
Целью данной контрольной работы является приобретение умения построения эконометрических моделей, принятие решений о спецификации и идентификации моделей, выбор метода оценки параметров модели, интерпретация результатов, получение прогнозных оценок.
Задачей данной работы является решение поставленных вопросов с помощью эконометрических методов. Данная работа позволит приобрести навыки использования различных эконометрических методов.
Задача 1
По данным, представленным в таблице выполнить следующие расчеты:
1. рассчитать параметры парной линейной регрессии.
2. оценить тесноту связи с помощью показателей корреляции и детерминации
3. оценить с помощью средней ошибки аппроксимации качество уравнений.
4. оценить статистическую зависимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдентов
5. рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 20% от его среднего уровня значимости α = 0,05
Решение.
Рассчитаем параметры парной линейной регрессии. Для этого выберем модель уравнения, построим уравнение тренда.
Для рассмотрения зависимости урожайности от дозы внесенных удобрений используем уравнение прямой:
y
=
a
+
bx
где х – независимый признак, доза внесенных удобрений
у – урожайность,
a, b – параметры уравнения регрессии.
Для расчетов параметров уравнения составим систему уравнений
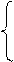 na
+
b
∑х = ∑у na
+
b
∑х = ∑у
a
∑х +
b
∑х2
= ∑ух
где n – число наблюдений, n=25
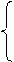 25а +86,5
b
= 256,9 25а +86,5
b
= 256,9
86,5
a
+ 844,941
b
= 995,969
Параметры а и b можно определить по формулам
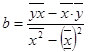 и a
=
y
-
bx и a
=
y
-
bx
b
= (39,839 – 3,46∙10,276)/ (33,798-3,462
) = 0,1960
а = 10,276 – 0,196∙3,46 = 9,598
ỹ = 9,598 + 0,196х
Коэффициент регрессии b= 0,196 ц/га показывает, насколько в среднем повысится урожайность при увеличении дозы внесения удобрений на 1 кг.
Средняя ошибка аппроксимации
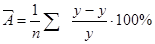 = 1/25 ∙494,486 = 19,780% = 1/25 ∙494,486 = 19,780%
Ошибка аппроксимации 19,78 % > 12% – модель ненадежна и статистически незначима.
Оценим тесноту связи с помощью показателей корреляции и детерминации.
Тесноту связи показывает коэффициент корреляции:
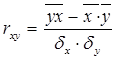
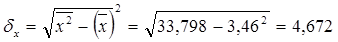
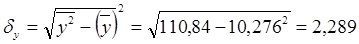
δx
- показывает, что в среднем фактор Х меняется в пределах
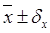 , 3,46 ± 4,672 , 3,46 ± 4,672
δу
- показывает, что в среднем фактор Y меняется в пределах
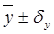 , 10,276 ± 2,289 , 10,276 ± 2,289
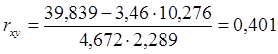
rxy
= 0,401, 0,3≤0,401≤0,5 – связь слабая
Коэффициент детерминации R = rxy
2
∙100% = 0,4012
∙100% = 16,08.
y
зависит от выбранного x
на 16,08%, на оставшиеся 100-16,08% y
зависит от других факторов.
Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.
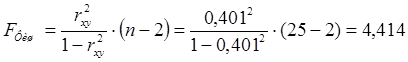
Приα = 0,05, κ1
= n-1, κ2
= n-2 =25-2 =23
Fтабл
.
= 2,00, FФиш.
= 4,414 > Fтабл.
= 2,00 – модель значима и надежна
Рассчитаем прогнозное значение результата с вероятностью 0,95% при повышении дозы внесения удобрений от своего среднего уровня и определим доверительный интервал прогноза.
Найдем точечный прогноз для хпрогноз
= 1,2∙х , хр
= 1,2 ∙3,46 = 4,152
ỹ =
a
+
bx
, ỹр
= 9,598 + 0,196∙
хр
= 9,598 + 0,196∙4,152 = 10,412
Найдем среднюю ошибку прогнозного значения
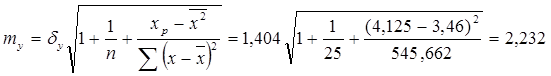
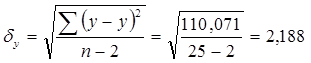
Fтабл.
Стьюдента для α = 0,05, df = n-2 = 25-2 = 23
tтабл.
=2,0687,
∆ур
= tтабл
∙станд.ошибка = 2,0687∙2,188 = 4,526
Доверительный интервал прогноза по урожайности
γур
= yp
± ∆ур
= 10,412 ± 4,526, от 5,886 до 14,938
Таблица 1. Исходные данные для задачи 1
| № |
Внесено мин.удобрений, ц |
Урожайность,
ц/га
|
Х2
|
у∙х |
У2
|
Урожайность расчетная,Ỹ |
(Y-Ỹ) |
(Y-Ỹ)/100 |
(Y-Ỹ)2
|
(Х-¯Х)2
|
| 1 |
13,9 |
9,4 |
193,21 |
130,66 |
88,36 |
12,322 |
-2,922 |
31,085 |
8,538 |
108,994 |
| 2 |
8,8 |
15 |
77,44 |
132 |
225 |
11,323 |
3,677 |
100,245 |
13,52 |
28,516 |
| 3 |
4 |
8,2 |
16 |
32,8 |
67,24 |
10,382 |
-2,182 |
26,610 |
4,761 |
0,292 |
| 4 |
0,01 |
8,2 |
0,0001 |
0,082 |
67,24 |
9,6 |
-1,4 |
17,073 |
1,96 |
11,903 |
| 5 |
4,2 |
13,7 |
17,64 |
57,54 |
187,69 |
10,421 |
3,279 |
23,934 |
10,752 |
0,548 |
| 6 |
0,7 |
9,2 |
0,49 |
6,44 |
84,64 |
9,735 |
-0,535 |
5,815 |
0,286 |
7,618 |
| 7 |
6,7 |
12,4 |
44,89 |
83,08 |
153,76 |
10,911 |
1,489 |
12,008 |
2,217 |
10,498 |
| 8 |
15,9 |
14 |
252,81 |
222,6 |
196 |
12,714 |
1,286 |
9,186 |
1,654 |
154,754 |
| 9 |
1,9 |
8,6 |
3,61 |
16,34 |
73,96 |
9,97 |
-1,37 |
15,930 |
1,877 |
2,434 |
| 10 |
1,9 |
14,7 |
3,61 |
27,93 |
216,09 |
9,97 |
4,73 |
32,177 |
22,373 |
2,434 |
| 11 |
0,01 |
6,3 |
0,0001 |
0,063 |
39,69 |
9,6 |
-3,3 |
52,381 |
10,89 |
11,903 |
| 12 |
0,01 |
8,5 |
0,0001 |
0,085 |
72,25 |
9,6 |
-1,1 |
12,941 |
1,21 |
11,903 |
| 13 |
0,01 |
8,8 |
0,0001 |
0,088 |
77,44 |
9,6 |
-0,8 |
9,091 |
0,64 |
11,903 |
| 14 |
1,2 |
10,9 |
1,44 |
13,08 |
118,81 |
9,833 |
1,067 |
9,789 |
1,138 |
5,108 |
| 15 |
0,01 |
9,2 |
0,0001 |
0,092 |
84,64 |
9,6 |
-0,4 |
4,348 |
0,16 |
11,903 |
| 16 |
0,01 |
13,4 |
0,0001 |
0,134 |
179,56 |
9,6 |
3,8 |
28,358 |
14,44 |
11,903 |
| 17 |
3,7 |
10,8 |
13,69 |
39,69 |
116,64 |
10,323 |
0,477 |
4,417 |
0,288 |
0,058 |
| 18 |
0,01 |
7,9 |
0,0001 |
0,079 |
62,41 |
9,6 |
-1,7 |
21,519 |
2,89 |
11,903 |
| 19 |
0,01 |
9,1 |
0,0001 |
0,091 |
82,81 |
9,6 |
-0,5 |
5,495 |
0,25 |
11,903 |
| 20 |
1,6 |
9,2 |
2,56 |
14,72 |
84,64 |
9,912 |
-0,712 |
7,739 |
0,507 |
3,460 |
| 21 |
2,5 |
10,3 |
6,25 |
25,75 |
106,09 |
10,088 |
0,212 |
2,058 |
0,045 |
0,922 |
| 22 |
0,01 |
11,1 |
0,0001 |
0,111 |
123,21 |
9,6 |
1,5 |
13,514 |
2,25 |
11,903 |
| 23 |
6,3 |
9,5 |
39,69 |
59,85 |
90,25 |
10,833 |
-1,333 |
14,032 |
1,777 |
8,066 |
| 24 |
0,01 |
8,4 |
0,0001 |
0,084 |
70,56 |
9,6 |
-1,2 |
14,286 |
1,44 |
11,903 |
| 25 |
13,1 |
10,1 |
171,61 |
132,31 |
102,01 |
12,166 |
-2,066 |
20,455 |
4,268 |
92,930 |
| Итого |
86,5 |
256,9 |
844,941 |
995,969 |
2770,99 |
256,903 |
0,003 |
494,486 |
110,071 |
545,662 |
| Среднее значение |
3,46 |
10,276 |
33,798 |
39,839 |
110,84 |
21,826 |
Задача 2
По данным представленным в таблице 3 изучается зависимость бонитировочного балла (У) от трех факторов.
С помощью ППП MSExcel:
1. Построить матрицу парных коэффициентов корреляции. Установить, какие факторы мультиколлинеарны.
2. Построить уравнение множественной регрессии в линейной форме с полным набором факторов.
3. Оценить статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.
4. Отобрать информативные факторы. Построить уравнение регрессии со статитически значимыми факторами.
5. Оценить полученные результаты, выводы оформить в аналитической записке.
В ППП MSExcel построим матрицу парных коэффициентов корреляции (сделать вставку из ексель зад.2).
По данным матрицы, определим мультиколлинеарность факторов, когда более чем два фактора связаны между собой линейной зависимостью. Из полученной матрицы видно, что зависимости между тремя данными факторами нет. Так rx
2
x
1
= -0,0732, rx
3
x
1
= 0,0427, rx
3
x
2
= -0,0886. Из всех трех факторов наиболее тесно связан с результатом фактор Х1
– доза внесения удобрения на посевную площадь, ryx
1
= 0,4004, затем фактор Х2
– коэффициент износа основных средств, , ryx
2
= 0,3858 и очень слабая зависимость от 3-го фактора Х3
, ryx
3
= 0,0264.
Построим уравнение множественной регрессии с полным набором факторов. Так как факторы не коррелируют между собой, то для включающего три объекта переменных уравнение множественной регрессии выглядит следующим образом:
y = a + b1
∙x1
+ b2
∙x2
+ b3
∙x3
+ ξ
С помощью ППП MSExcel найдем значения а и b:
b = 13,9661, а1
= 0,1837, а2
= - 0,0917, а3
= 0,0022
Итак, уравнение множественной регрессии с полным набором факторов будет следующим:
y = 13,9661 + 0,1837х1
- 0,0917x2
+ 0,0022x3
Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента. Значимость уравнения множественной регрессии оценивается с помощью F-критерия Фишера:
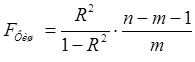
где R2
– коэффициент множественной регрессии,
m – число параметров при переменных х,
n – число наблюдений.
R= 0,5369
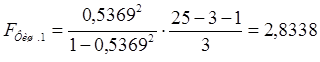
Fтаб
= при 5%-ном уровне значимости для числа степеней свободы 1 и 21 равно 4,32.
Fфакт
< Fтаб
– модель незначима и ненадежна.
Для того чтобы модель была надежна уберем из нее фактор х3
, так как он меньше всего коррелирует с у.
Получим уравнение:
y = 14,1136 + 0,1837х1
- 0,0917x2
Значимость уравнения множественной регрессии по F-критерию составляет Fфакт
= 4,45. Так как Fфакт
= 4,45 > Fтаб
= 4,35, то модель значима и надежна.
Итак, составив уравнение множественной регрессии и включив в него три фактора, определила, что с помощью F-критерия Фишера полученная модель незначима и ненадежна. Затем исключила из модели наиболее незначимый признак X3
, так как он имеет наименьший коэффициент корреляции с результативным показателем. По полученному уравнению регрессии видно, что средняя урожайность составляет 14,1136 ц/га увеличится на 0,1837 ц/га при повышении дозы внесения удобрения на 1 ц, и уменьшится на 0,0917 ц/га при повышении коэффициента износа основных средств на 1 единицу.
Задача 3
По учебнику задача №37
1.Найти коэффициенты автокорреляции разного порядка и выберите величину лага.
2.Построить авторегрессионную функцию.
3. Рассчитать прогнозные значения на три года вперед.
В таблице 4 приводятся сведения об уровне среднегодовых цен на говядину из США на рынках Нью-Йорка, амер.центы за фунт.
Данная задача относится к типу задач на моделирование временных рядов. Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно разделить на три группы:
- факторы, формирующие тенденцию ряда;
- факторы, формирующие циклические колебания ряда;
- случайные факторы.
Нанесем значения нашей задачи на график (рисунок 1).
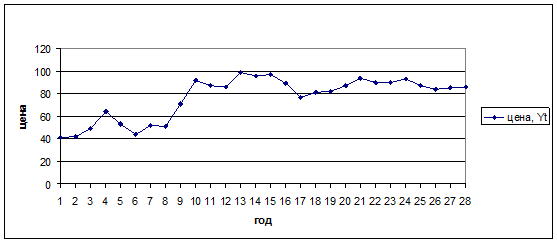
Из структуры графика видно, что основной компонентой временного ряда является возрастающая компонента.
Найдем коэффициенты автокорреляции разного порядка и выберем величину лага.
Расчет коэффициента автокорреляции первого порядка для временного ряда расходов на конечное потребление
| t |
yt
|
Yt-1
|
yt
-y1
|
Yt-1
-y2
|
(yt
-y1
)( Yt-1
-y2
) |
(Yt-1
-y1
)2
|
(Yt-1
-y2
)2
|
| 1 |
41 |
- |
- |
- |
- |
- |
- |
| 2 |
42 |
41 |
-36,07 |
-35,41 |
1277,24 |
1301,04 |
1253,87 |
| 3 |
49 |
42 |
-29,07 |
-34,41 |
1000,29 |
845,06 |
1184,05 |
| 4 |
64 |
49 |
-14,07 |
-27,41 |
385,66 |
197,9 |
751,31 |
| 5 |
53 |
64 |
-25,07 |
-12,41 |
311,12 |
628,5 |
154 |
| 6 |
44 |
53 |
-34,07 |
-23,41 |
797,58 |
1160,76 |
548,03 |
| 7 |
52 |
44 |
-26,07 |
-32,41 |
844,93 |
679,6 |
1050,41 |
| 8 |
51 |
52 |
-27,07 |
-24,41 |
660,78 |
732,8 |
595,85 |
| 9 |
71 |
51 |
-7,07 |
-25,41 |
179,65 |
50 |
645,67 |
| 10 |
92 |
71 |
13,93 |
-5,41 |
-75,36 |
194,04 |
29,27 |
| 11 |
87 |
92 |
8,93 |
15,59 |
139,22 |
79,75 |
243,05 |
| 12 |
86 |
87 |
7,93 |
10,59 |
83,98 |
62,89 |
112,15 |
| 13 |
99 |
86 |
20,93 |
9,59 |
200,72 |
438,06 |
91,97 |
| 14 |
96 |
99 |
17,93 |
22,59 |
359,86 |
321,48 |
510,31 |
| 15 |
97 |
96 |
18,93 |
19,59 |
370,84 |
358,34 |
383,77 |
| 16 |
89 |
97 |
10,93 |
20,59 |
225,05 |
119,46 |
423,95 |
| 17 |
77 |
89 |
-1,07 |
12,59 |
-13,47 |
1,14 |
383,77 |
| 18 |
81 |
77 |
2,93 |
0,59 |
1,73 |
8,58 |
0,35 |
| 19 |
82 |
81 |
3,93 |
4,59 |
18,04 |
15,44 |
21,07 |
| 20 |
87 |
82 |
8,93 |
5,59 |
49,92 |
79,74 |
31,25 |
| 21 |
94 |
87 |
15,93 |
10,59 |
168,7 |
253,76 |
112,15 |
| 22 |
90 |
94 |
11,93 |
17,59 |
209,85 |
142,32 |
309,41 |
| 23 |
90 |
90 |
11,93 |
13,59 |
162,13 |
142,32 |
184,69 |
| 24 |
93 |
90 |
14,93 |
13,59 |
202,9 |
222,9 |
184,69 |
| 25 |
87 |
93 |
15,93 |
16,59 |
264,28 |
253,76 |
275,23 |
| 26 |
84 |
87 |
5,93 |
10,59 |
62,8 |
35,16 |
112,15 |
| 27 |
85 |
84 |
6,93 |
7,59 |
52,6 |
48,02 |
57,61 |
| 28 |
86 |
85 |
7,93 |
8,59 |
68,12 |
62,88 |
73,79 |
| 2149 |
2063 |
9,25 |
11,02 |
8016,65 |
8435,7 |
9723,82 |
y1
= ∑ уt
/ (n-1) =
(42+49+64+53+44+52+51+71+92+87+86+99+96+97+89+77+81+82+87+9
4+90+90+93+87+84+85+86)/27= 2149/27 = 78,07
у2
= ∑ уt-1
/ (n-1) =
(41+42+49+64+53+44+52+51+71+92+87+86+99+96+97+89+77+81+82+8
7+94+90+90+93+87+84+85)/27 = 2063/27 = 76,41

r1
= 8016.65/ √(8435,7 х 9723,82) = 0,8951
Таблица Расчет коэффициента автокорреляции второго порядка для временного ряда расходов на конечное потребление
| t |
yt |
Yt-2 |
yt-y2 |
Yt-2-y2 |
(yt-y2)( Yt-2-y2) |
(Yt-2-y2)2 |
(Yt-2-y2)2 |
| 1 |
41 |
- |
- |
- |
- |
- |
- |
| 2 |
42 |
- |
- |
- |
- |
- |
- |
| 3 |
49 |
41 |
-33,65 |
-35,08 |
1180,44 |
1132,32 |
1230.60 |
| 4 |
64 |
42 |
-18,65 |
-34,08 |
635,6 |
347,82 |
1161.45 |
| 5 |
53 |
49 |
-29,65 |
-27,08 |
802,92 |
879,12 |
733.33 |
| 6 |
44 |
64 |
-38,65 |
-12,08 |
466,89 |
1493,82 |
145,93 |
| 7 |
52 |
53 |
-30,65 |
-23,08 |
707,4 |
939,42 |
532,69 |
| 8 |
51 |
44 |
-31,65 |
-32,08 |
1015,33 |
1001,72 |
1029,13 |
| 9 |
71 |
52 |
-11,65 |
-24,08 |
280,53 |
135,72 |
579,85 |
| 10 |
92 |
51 |
9,35 |
-25,08 |
-234,5 |
87,42 |
629,01 |
| 11 |
87 |
71 |
4,35 |
-5,08 |
-22,1 |
18,92 |
25,81 |
| 12 |
86 |
92 |
3,35 |
15,92 |
53,33 |
11,22 |
253,45 |
| 13 |
99 |
87 |
16,35 |
10,92 |
178,54 |
267,32 |
119,25 |
| 14 |
96 |
86 |
13,35 |
9,92 |
132,43 |
178,22 |
98,41 |
| 15 |
97 |
99 |
14,35 |
22,92 |
328,9 |
205,92 |
525,33 |
| 16 |
89 |
96 |
6,35 |
19,92 |
126,5 |
40,32 |
396,81 |
| 17 |
77 |
97 |
-5,65 |
20,92 |
-118,2 |
31,92 |
437,65 |
| 18 |
81 |
89 |
-1,65 |
12,92 |
-21,32 |
2,72 |
166,93 |
| 19 |
82 |
77 |
-0,65 |
0,92 |
-0,6 |
0,42 |
085 |
| 20 |
87 |
81 |
4,35 |
4,92 |
21,4 |
18,92 |
24,21 |
| 21 |
94 |
82 |
11,35 |
5,92 |
67,2 |
128,82 |
35,05 |
| 22 |
90 |
87 |
7,35 |
10,92 |
80,26 |
54,02 |
119,25 |
| 23 |
90 |
94 |
7,35 |
17,92 |
131,71 |
54,02 |
321,13 |
| 24 |
93 |
90 |
10,35 |
13,92 |
144,07 |
107,12 |
193,77 |
| 25 |
87 |
90 |
4,35 |
13,92 |
60,55 |
18,92 |
193,77 |
| 26 |
84 |
93 |
1,35 |
16,92 |
22,84 |
1,82 |
286,29 |
| 27 |
85 |
87 |
2,35 |
10,92 |
25,66 |
5,52 |
119,25 |
| 28 |
86 |
84 |
3,35 |
7,92 |
26,53 |
11,22 |
62,73 |
| 2149 |
1978 |
6092,31 |
7174,72 |
9422,38 |
y1
= ∑ уt
/ (n-1) =
(42+49+64+53+44+52+51+71+92+87+86+99+96+97+89+77+81+82+87+9
4+90+90+93+87+84+85+86)/27= 2149/26 = 82,65
у2
= ∑ уt-1
/ (n-1) =
(41+42+49+64+53+44+52+51+71+92+87+86+99+96+97+89+77+81+82+8
7+94+90+90+93+87+84)/27 = 1978/26 = 76,08
r2
= 6092,31/√ (7174,72 х 9422,38) = 0,7410
Итак, коэффициент корреляции первого порядка r1
= 0,8961
коэффициент корреляции второго порядка r2
= 0,7550
Автоматически в ППП Exel рассчитаем коэффициент корреляции третьего порядка r3
= 0,6546, и коэффициент корреляции четвертого порядка r4
= 0,5461
Как видно из полученных данных, наиболее тесная зависимость между среднегодовыми ценами на говядину в США и текущим или предшествующими годами происходит при сдвиге ряда данных на 1 год ( или 1 лаг) r1
= 0,8951.
Рассчитав коэффициенты автокорреляции 1, 2, 3, 4-го порядков получили автокорреляционную функцию этого ряда. Анализ значений автокорреляционной функции позволяет сделать выводы о наличии в изучаемом временном ряде тенденции.
Для того, чтобы рассчитать прогноз цен на три года вперед, составим уравнение тренда для временного ряда показателей среднегодовых цен на говядину.
У = а +
bt
,
Где У – выравненное значение среднегодовой цены,
b
,
t
- неизвестные параметры,
а
– начальный уровень временного ряда в момент времени t=0.
b
– ежегодный прирост (снижение) цены на говядину,
t
– значение дат.
Для определения неизвестных параметров a и b в соответствии с требованием способа наименьших квадратов необходимо решить систему нормальных уравнений:
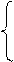 na
+
b
∑
t
= ∑
Y na
+
b
∑
t
= ∑
Y
a
∑
t
+
b
∑
t
2
= ∑
Yxt
Для упрощения системы воспользуемся способом отсчета от условного начала.
Поскольку ∑
t
= 0,
система уравнений примет вид:
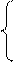 na
= ∑
Y na
= ∑
Y
b
∑
t
2
= ∑
Yxt
,
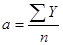 , , 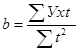
a=(41+42+49+64+53+44+52+51+71+92+87+86+99+96+97+89+77+81+82
+87+94+90+90+93+87+84+85+86) / 28 = 76,75
b = 12920/ 1638 = 7,8877
y = 76,75 + 7,89t
Т.е. уравнение линейного тренда имеет вид y = 76,75 + 7,89t. Это означает, что средняя фактическая и выровненная цена, отнесенная к середине периода, т.е. к 1983 г. равна 76,75 амер.центов за фунт, а среднегодовой прирост цены составляет 7,89 центов за фунт.
Таблица 3. Расчет параметров уравнения тренда
№
года
|
Годы |
Среднегодовая цена на говядину, У |
Условное обозначение периодов,
T
|
t2
|
Y x t |
| 1 |
1970 |
41 |
-13 |
169 |
533 |
| 2 |
1971 |
42 |
-12 |
144 |
504 |
| 3 |
1972 |
49 |
-11 |
121 |
539 |
| 4 |
1973 |
64 |
-10 |
100 |
640 |
| 5 |
1974 |
53 |
-9 |
81 |
477 |
| 6 |
1975 |
44 |
-8 |
64 |
352 |
| 7 |
1976 |
52 |
-7 |
49 |
364 |
| 8 |
1977 |
51 |
-6 |
36 |
306 |
| 9 |
1978 |
71 |
-5 |
25 |
355 |
| 10 |
1979 |
92 |
-4 |
16 |
368 |
| 11 |
1980 |
87 |
-3 |
9 |
261 |
| 12 |
1981 |
86 |
-2 |
4 |
172 |
| 13 |
1982 |
99 |
-1 |
1 |
99 |
| 14 |
1983 |
96 |
0 |
0 |
0 |
| 15 |
1984 |
97 |
1 |
1 |
97 |
| 16 |
1985 |
89 |
2 |
4 |
178 |
| 17 |
1986 |
77 |
3 |
9 |
231 |
| 18 |
1987 |
81 |
4 |
16 |
324 |
| 19 |
1988 |
82 |
5 |
25 |
410 |
| 20 |
1989 |
87 |
6 |
36 |
522 |
| 21 |
1990 |
94 |
7 |
49 |
658 |
| 22 |
1991 |
90 |
8 |
64 |
720 |
| 23 |
1992 |
90 |
9 |
81 |
810 |
| 24 |
1993 |
93 |
10 |
100 |
930 |
| 25 |
1994 |
87 |
11 |
121 |
957 |
| 26 |
1995 |
84 |
12 |
144 |
1008 |
| 27 |
1996 |
85 |
13 |
169 |
1105 |
| Итого |
2063 |
0 |
1638 |
12920 |
По полученному уравнению (функции) можно составить прогнозные оценки: точечные прогнозы и доверительные интервалы прогноза.
Номер прогнозируемого периода будем отсчитывать от 1983 года, когда t=0, тогда t1999
= 16 (1999г.), тогда точечный прогноз удоя молока на 1 гол. на 2000 год составит
У31
= 76,75 + 7,89 х 16 = 202,99
Таким образом, по уравнению тренда стоимость 1 фунта говядины в 1999 г. составила 202,99 американских центов.
Библиографический список
1. Эконометрика/ Под ред. И.И. Елисеевой.- М.: Финансы и статистика, 2004. – 344 с.
2. Практикум по эконометрике/ Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. – 192 с.
3. Общая теория статистики/ Под ред. И.И. Елисеевой.- М.: Финансы и статистика, 2001. – 480 с.
4. Бакирова Р.Р. Эконометрика. Методические указания по выполнению контрольных работ, - БГАУ, 2007. – 7 с.
|