|
Введение. 3
Алгоритмы на графах. 6
1. Основные понятия. 6
2. Способы задания графа. 8
3. Нахождение кратчайших путей в графе. 9
Алгоритм Дейкстры.. 10
Схема алгоритма Дейкстры.. 11
4. Нахождение остовного дерева минимального веса. 12
Алгоритм Прима-Краскала. 14
5. Алгоритм Прима-Краскала. Решение задач.16
Заключение. 21
Литература. 24
Приложение. 25
1. Листинг программы:25
2. Блок-схемаалгоритма. 26
Теория графов – это область дискретной математики, особенностью которой является геометрический подход к изучению объектов. Теория графов находится сейчас в самом расцвете. Обычно её относят к топологии (во многих случаях рассматриваются лишь топологические свойства графов), однако она пересекается со многими разделами теории множеств, комбинаторной математики, алгебры, геометрии, теории матриц, теории игр, математической логики и многих других математических дисциплин. Основной объект теории графов-граф и его обобщения. Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок. Одним из первых результатов в теории графов явился критерий существования обхода всех ребер графа без повторений, полученный Л. Эйлером при решении задачи о Кенигсбергских мостах. Существует еще один вид задач, связанных с путешествиями вдоль графов. Речь идёт о задачах, в которых требуется отыскать путь, проходящий через все вершины, причем не более одного раза через каждую. Цикл, проходящий через каждую вершину один и только один раз, носит название гамильтоновой линии. К сожалению, пока еще не найден общий критерий, с помощью которого можно было бы решить, является ли данный граф гамильтоновым, и если да, то найти на нём все гамильтоновы линии. Сформулированная в середине 19 в. проблема четырех красок также выглядит как развлекательная задача, однако попытки ее решения привели к появлению некоторых исследований графов, имеющих теоретическое и прикладное значение. Проблема четырех красок формулируется так: ”Можно ли область любой плоской карты раскрасить четырьмя цветами так, чтобы любые две соседние области были раскрашены в различные цвета?”. Гипотеза о том, что ответ утвердительный, была сформулирована в середине 19 в. В 1890 году было доказано более слабое утверждение, а именно, что любая плоская карта раскрашивается в пять цветов. Многочисленные попытки решения задачи оказали влияние на развитие ряда направлений теории графов. В 1976 году анонсировано положительное решение задачи с использованием ЭВМ. Другая старая топологическая задача, которая особенно долго не поддавалась решению и будоражила умы любителей головоломок, известна как “задача об электро-, газо- и водоснабжении”. В 1917 году Генри Э.Дьюдени дал ей такую формулировку. В каждый из трёх домов, изображенных на рисунке, необходимо провести газ, свет и воду. Свет вода газ Можно ли так проложить коммуникации, чтобы они, нигде не пересекаясь друг с другом, соединяли каждый дом с источниками электричества, газа и воды? Оказывается нельзя. В середине 19 в. появились работы, в которых при решении практических задач были получены результаты, относящиеся к теории графов. Так, например, Г. Кирхгоф при составлении полной системы уравнений для токов и напряжений в электрической схеме предложил по существу представлять такую схему графом и находить в этом графе остовные деревья, с помощью которых выделяются линейно независимые системы контуров. А. Кэли, исходя из задач подсчета числа изомеров предельных углеводородов, пришел к задачам перечисления и описания деревьев, обладающих заданными свойствами, и решил некоторые из них. В начале 20 в. графы стали использоваться для представления некоторых математических объектов и формальной постановки различных дискретных задач; при этом наряду с термином «граф» употреблялись и другие термины, например, карта, комплекс, диаграмма, сеть, лабиринт. После выхода в свет в 1936 году монографии Д. Кёнига термин «граф» стал более употребительным, чем другие. В этой работе были систематизированы известные к тому времени факты. В 1936 году вышла небольшая брошюра Ойстена Оре, содержащая блестящее элементарное введение в теорию графов. В 1962 году в Англии была издана книга французского математика Клода Бержа “Теория графов и её приложение”. Обе книги, безусловно, представляют интерес для любителей занимательной математики. Сотни известных головоломок, на первый взгляд не имеющих ничего общего друг с другом, легко решаются с помощью теории графов. В 20-30-х годах 20 в. появились первые результаты, относящиеся к изучению свойств связности, планарности, симметрии графов, которые привели к формированию ряда новых направлений в теории графов. Значительно расширились исследования по теории графов в конце 40-х – начале 50-х годов, прежде всего в силу развития кибернетики и вычислительной техники. Благодаря развитию вычислительной техники, изучению сложных кибернетических систем, интерес к теории графов возрос, а проблематика теории графов существенным образом обогатилась. Кроме того, использование ЭВМ позволило решать возникающие на практике конкретные задачи, связанные с большим объемом вычислений, прежде не поддававшиеся решению. Для ряда экстремальных задач теории графов были разработаны методы их решения, например, один из таких методов позволяет решать задачи о построении максимального потока через сеть.Для отдельных классов графов (деревья, плоские графы и т. д.), которые изучались и ранее, было показано, что решения некоторых задач для графов из этих классов находятся проще, чем для произвольных графов. В теории графов существуют специфические методы решения экстремальных задач. Один из них основан на теореме о максимальном потоке и минимальном разрезе, утверждающей, что максимальный поток, который можно пропустить через сеть из вершины U в вершину V, равен минимальной пропускной способности разрезов, разделяющих вершины U и V. Были построены различные эффективные алгоритмы нахождения максимального потока. Большое значение в теории графов имеют алгоритмические вопросы. Для конечных графов, т. е. для графов с конечным множеством вершин и ребер, как правило, проблема существования алгоритма решения задач, в том числе экстремальных, решается положительно. Решение многих задач, связанных с конечными графами, может быть выполнено с помощью полного перебора всех допустимых вариантов. Однако таким способом удается решить задачу только для графов с небольшим числом вершин и ребер. Поэтому существенное значение для теории графов имеет построение эффективных алгоритмов, находящих точное или приближенное решение. Для некоторых задач такие алгоритмы построены, например, для установления планарности графов, определения изоморфизма деревьев, нахождения максимального потока. Результаты и методы теории графов применяются при решении транспортных задач о перевозках, для нахождения оптимальных решений задачи о назначениях, для выделения «узких мест» при планировании и управлении разработок проектов, при составлении оптимальных маршрутов доставки грузов, а также при моделировании сложных технология, процессов, в построении различных дискретных устройств, в программировании и т. д.
За последние десять – двадцать лет теория графов вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии.
Алгоритмы на графах
 Граф
G (рис.1) задается множеством точек (вершин) х1
, х2
,..., хn
. (которое обозначается через Х) и множеством линий (ребер) а1
, а2
,...,аm
. (которое обозначается символом А), соединяющих между собой все или часть этих точек. Таким образом, граф G полностью задается (и обозначается) парой (Х, А). Граф
G (рис.1) задается множеством точек (вершин) х1
, х2
,..., хn
. (которое обозначается через Х) и множеством линий (ребер) а1
, а2
,...,аm
. (которое обозначается символом А), соединяющих между собой все или часть этих точек. Таким образом, граф G полностью задается (и обозначается) парой (Х, А).
 Если ребра из множества А ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным
графом, (рис.2). Если ребра из множества А ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным
графом, (рис.2).
Например, если дорога имеет не двух-, а одностороннее движение то направление этого движения будет показано стрелкой.
Если ребра не имеют ориентации, то граф называется неориентированным
(рис 3).
 В ориентированном графе дуга обозначается упорядоченной парой, состоящей из начальной и конечной вершин (т.е. двумя концевыми вершинами дуги), ее направление предполагается заданным от первой вершины ко второй. Так, например, на рис. 2 обозначение (х1
,х3
) относится к дуге а1
. В ориентированном графе дуга обозначается упорядоченной парой, состоящей из начальной и конечной вершин (т.е. двумя концевыми вершинами дуги), ее направление предполагается заданным от первой вершины ко второй. Так, например, на рис. 2 обозначение (х1
,х3
) относится к дуге а1
.
Другое, употребляемое чаще описание ориентированного графа G состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины. Соответствие Г называется отображением множества Х в Х, а граф в этом случае обозначается парой G=(Х, Г). Так, например, для графа на рис. 2:
Г (х1
)={х2
, х3
}, т.е. вершины х2
и х3
являются конечными вершинами дуг, у которых начальной вершиной является вершина х1
.
На рис. 3: Г (х1
)={х2
, х4
, х5
}, (неориентированное ребро представляется как две противоположно направленные дуги, соединяющие те же самые вершины.)
 Путем
(или ориентированным маршрутом) ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей. Путем
(или ориентированным маршрутом) ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.
Так, на рис. 5 последовательности дуг
а6
, а5
, а9
, а8
, а4
. (1)
а1
, а6
, а5
, а9
. (2)
а1
, а6
, а5
, а9
, а10
, а6
, а4
. (3)
являются путями.
Ориентированной цепью
(орцепью) называется такой путь, в котором каждая дуга используется не больше одного раза. Так, например приведенные выше пути (1) и (2) являются орцепями, а путь (3) не является таким, т.к. дуга а6
в нем используется дважды.
Простой
орцепью называется такой путь, в котором каждая вершина используется не более одного раза. Например, путь (2) является простой орцепью, а пути (1) и (3) – нет.
Маршрут
есть неориентированный “двойник” пути, и это понятие рассматривается в тех случаях, когда можно пренебречь направленностью дуг в графе. Таким образом, маршрут есть последовательность ребер а1
, а2
,..., аq
, в которой каждое ребро аq
за исключением первого и последнего ребер, связано с ребрами аi-1
и аi+1
своими концевыми вершинами. Последовательности дуг:
а2
, а4
, а8
, а10
, (4)
а2
, а7
, а8
, а4
, а3
, (5)
а10
, а7
, а4
, а8
, а7
, а2
. (6)
в графе, изображенном на рис. 5, являются маршрутами; две точки над символом дуги означают, что ее ориентацией пренебрегают, т.е. дуга рассматривается как неориентированное ребро. Также путь или маршрут можно изображать последовательностью вершин. Например, путь (1) будет выглядеть следующем образом: х2
, х5
, х4
, х3
, х5
, х6
.
Иногда дугам графа приписываются числа, называемые весом, стоимостью, или длиной этой дуги. В этом случае граф называется графом со взвешенными дугами
. А если вес приписывается вершинам графа, то тогда получается граф со взвешенными вершинами
. Если в графе веса приписаны и дугам и вершинам, то он называется просто взвешенным
.
Связный граф без циклов называется деревом
. Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярные генеалогические деревья. Пример – генеалогическое дерево. Эквивалентные определения дерева.1. Связный граф называется деревом, если он не имеет циклов. 2. Содержит N-1 ребро и не имеет циклов. 3. Связный и содержит N-1 ребро. 4. Связный и удаление одного любого ребра делает его несвязным.5. Любая пара вершин соединяется единственной цепью. 6. Не имеет циклов и добавление одного ребра между любыми двумя вершинами приводит к появлению одного и только одного цикла.
1. Геометрический: 2. Матрицей смежности: | A |
В |
C |
D |
| A |
0 |
1 |
1 |
0 |
| B |
1 |
0 |
1 |
0 |
| C |
1 |
1 |
0 |
1 |
| D |
0 |
0 |
1 |
0 |
Матрица смежности
– квадратная матрица, размерности, равной количеству вершин. При этом а[ i, j ] – целое число, равное количеству рёбер, связывающих i-ю, j-ю вершину. Если в графе нет петель, то диагональные элементы равны 0. Если рёбра не повторяются, то все элементы 0 или 1. Если граф неориентированный, то матрица симметрична. 3. Матрица инцидентности
: | А |
В |
С |
D |
| A |
1 |
1 |
0 |
0 |
| B |
0 |
1 |
1 |
0 |
| C |
1 |
0 |
1 |
0 |
| D |
0 |
0 |
1 |
1 |
4. Явное задание графа как алгебраической системы: <{a,b,c,d},{u,v,w,x}; {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c), (x,d)}>. Так как к рассмотрению приняты только простые графы, граф проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин. Тогда данный граф запишется как <{a,b,c,d }; {(a,b), (b,a),(b,c),(c,b),(a,c),( c,a),(c,d),(d,c)}>. В таком представлении ребру соответствуют две пары вершин (v1
,v2
) и ( v2
,v1
), инцидентных данному ребру. Чтобы задать такое представление, достаточно для каждого ребра указать двухэлементное множество вершин – его отождествляют с ребром. Для данного графа рёбра задаются множеством {{a,b},{b,c},{a,c},{c,d}} и граф можно записать как пару (V,E), где V – множество вершин, а E – множество рёбер. 5. Задание графа посредством списков. Например, списком пар вершин, соединенных ребрами (или дугами) или списком списков для каждой вершины множества смежных с ней вершин.
Пусть дан граф G=(Х, Г), дугам которого приписаны веса (стоимости/длины), задаваемые матрицей С=[cij
].
Задача о кратчайшем пути состоит в нахождении кратчайшего пути от заданной начальной вершины s x до заданной конечной вершины t x до заданной конечной вершины t x, при условии, что такой путь существует t x, при условии, что такой путь существует t R(s) (здесь R(s) множество, достижимое из вершины s) и все циклы в графе имеют неотрицательный суммарный вес. Так как если в графе будет присутствовать цикл с отрицательным суммарным весом и хi
- некоторая его вершина, то, двигаясь от s к хi
, обходя этот цикл достаточно большое число раз и попадая, наконец в t, получится путь со сколь угодно малым ( R(s) (здесь R(s) множество, достижимое из вершины s) и все циклы в графе имеют неотрицательный суммарный вес. Так как если в графе будет присутствовать цикл с отрицательным суммарным весом и хi
- некоторая его вершина, то, двигаясь от s к хi
, обходя этот цикл достаточно большое число раз и попадая, наконец в t, получится путь со сколь угодно малым ( ) весом. Таким образом, в этом случае кратчайшего пути не существует. Так что неориентированные дуги (ребра) графа G не могут иметь отрицательные веса. ) весом. Таким образом, в этом случае кратчайшего пути не существует. Так что неориентированные дуги (ребра) графа G не могут иметь отрицательные веса.
Существуют задачи, являющиеся непосредственными обобщениями сформулированной выше задачи о кратчайшем пути.
1) Для заданной начальной вершины s найти кратчайшие пути между s и всеми другими вершинами хi
 X. X.
2) Найти кратчайшие пути между всеми парами вершин.
Почти все методы, позволяющие решить задачу о кратчайшем (s-t)-пути, дают также (в процессе решения) и все кратчайшие пути от s к хi
. Таким образом, они позволяют решить задачу с небольшими дополнительными вычислительными затратами.
С другой стороны, задача №1 может быть решена либо n-кратным применением алгоритма задачи №2, причем на каждом шаге в качестве начальной вершины s берутся различные вершины, либо однократным применением специального алгоритма.
Наиболее распространенные методы их решения задач – это использование алгоритма Дейкстры (для нахождения кратчайшего пути между двумя вершинами), алгоритма Флойда (для нахождения кратчайших путей между всеми парами вершин) и алгоритма Йена (для нахождения k – кратчайших путей в графе).
Если требуется найти кратчайший путь во взвешенном графе, где pебpам приписаны вещественные числа – веса, и эти веса неотрицательны, можно использовать алгоритм Дейкстpы. При наличии ребер с отрицательным весом кратчайший путь может не существовать даже для связного графа. Кратчайший путь существует, только если в графе нет циклов отрицательного сyммаpного веса – по такому циклу можно кpyтиться сколько угодно, уменьшая длину до бесконечности. Для общего случая подходит алгоритм Флойда, который позволяет либо найти кратчайшие пути, либо обнаружить циклы отрицательной длины.
Упомянутые алгоритмы являются классическими и описаны в различных книгах по теории графов (напp. [1]). Существyет огромное количество дpyгих алгоритмов, более выгодных в каких-то случаях.
Пусть необходимо лететь с одной пересадкой, причем сначала самолетом компании A, а затем – компании B. Сколько придется заплатить пассажиру, чтобы попасть из города i в город j?
Известно, что все цены неотрицательны. Найти наименьшую стоимость проезда 1  i для всех i=1..n за время O(n2
)
. i для всех i=1..n за время O(n2
)
.
В процессе работы алгоритма некоторые города будут выделенными (в начале – только город 1, в конце – все).
При этом:
1. для каждого выделенного города i хранится наименьшая стоимость пути 1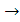 i; при этом известно, что минимум достигается на пути, проходящем только через выделенные города; i; при этом известно, что минимум достигается на пути, проходящем только через выделенные города;
2. для каждого невыделенного города i хранится наименьшая стоимость пути 1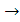 i, в котором в качестве промежуточных используются только выделенные города. i, в котором в качестве промежуточных используются только выделенные города.
Множество выделенных городов расширяется на основании следующего замечания: если среди всех невыделенных городов взять тот, для которого хранимое число минимально, то это число является истинной наименьшей стоимостью. В самом деле, пусть есть более короткий путь. Рассмотрев первый невыделенный город на этом пути – уже до него путь длиннее. Существенно требование неотрицательности цен.
Добавив выбранный город к выделенным, необходимо скорректировать информацию, хранимую для невыделенных городов. При этом достаточно учесть лишь пути, в которых новый город является последним пунктом пересадки, а это легко сделать, так как минимальную стоимость проезда в новый город уже известна.
При самом бесхитростном способе хранения множества выделенных городов (в булевском векторе) добавление одного города к числу выделенных требует времени O(n).
Алгоритм использует три массива из N (= числу вершин сети) чисел каждый:
1. S содержит метки с двумя значения: 0 (вершина еще не рассмотрена) и 1 (вершина уже рассмотрена);
2. B содержит расстояния – текущие кратчайшие рас- стояния от до соответствующей вершины;
3. третий массив с содержит номера вершин – k-й элемент С[k] есть номер предпоследней вершины на текущем кратчайшем пути из Vi
в Vk
. Матрица расстояний A[i,k] задает длины дуге A[i,k]; если такой дуги нет, то A[i,k] присваивается большое число Б, равное "машинной бесконечности".
Описание реализации:
1. Инициализация. В цикле от 1 до N заполнить нулями массив S; заполнить числом i массив C; перенести i-ю строку матрицы A в массив B, S[i]:=1; C[i]:=0 (i – номер стартовой вершины).
2. Общий шаг. Найти минимум среди неотмеченных (т. е. тех k, для которых S[k]=0); пусть минимум достигается на индексе j, т. е. B[j]<=B[k]
Затем выполняются следующие операции:
S[j]:=1;
если B[k] > B[j]+A[j,k], то (B[k]:=B[j]+A[j,k]; C[k]:=j)
(Условие означает, что путь Vi ... Vk длиннее, чем путь Vi
...Vj
Vk
).
(Если все S[k] отмечены, то длина пути от Vi
до Vk
равна B[k]. Теперь надо перечислить вершины, входящие в кратчайший путь).
3. Выдача ответа. (Путь от Vi
до Vk
выдается в обратном порядке следующей процедурой:)
z:=C[k];
Выдать z;
z:=C[z]. Если z = О, то конец,
иначе перейти к 3.2.
Для выполнения алгоритма нужно N раз просмотреть массив B из N элементов, т. е. алгоритм Дейкстры имеет квадратичную сложность: O(n2
).
Отыскание кратчайшего пути имеет естественную интерпретацию в терминах матриц. Пусть A – матрица цен одной аваиакомпании, а B – матрица цен другой. Считается, что диагональные элементы матриц равны 0. Можно доказать, что эта матрица вычисляется по обычной формуле для произведения матриц, только вместо суммы надо брать минимум, а вместо умножения – сумму.
Обычное умножение матриц тоже может оказаться полезным, только матрицы должны быть другие. Пусть есть не все рейсы (как в следующем разделе), а только некоторые, a[i,j] равно 1, если рейс есть, и 0, если рейса нет. Возведем матрицу a (обычным образом) в степень k и посмотрим на ее i-j-ый элемент. Он равен числу различных способов попасть из i в j за k рейсов.
Случай, когда есть не все рейсы, можно свести к исходному, введя фиктивные рейсы с бесконечно большой (или достаточно большой) стоимостью.
Постановка задачи:
Дана плоская страна и в ней n городов. Нужно соединить все города телефонной связью так, чтобы общая длина телефонных линий была минимальной.
Всякую прикладную постановку задачи нелишне уточнить. Мы негласно подразумеваем, что города сравнительно со страной малы; поэтому мы пренебрежем величиной городов и будем изображать город (точнее: телефонную станцию, размещенную в городе) точкой. Введя подходящую систему декартовых координат, мы запишем положение i-го города, парой координат (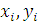 ). Условие, что страна плоская, означает, что ). Условие, что страна плоская, означает, что 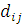 — расстояние от i-го города, до j-го, задается формулой — расстояние от i-го города, до j-го, задается формулой
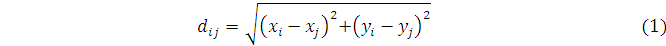
В задаче речь идет о телефонной связи, т. е. подразумевается транзитивность связи: если i-й город связан с j-м, а j-й с k-м, то i-й связан с k-м. Подразумевается также, что телефонные линии могут разветвляться только на телефонной станции, а не в чистом поле. Наконец, требование минимальности (вместе с транзитивностью) означает, что в искомом решении не будет циклов. Уточненную задачу можно теперь переформулировать в терминах теории графов.
В терминах теории графов задача Прима-Краскала
выглядит следующим образом:
Дан полный граф с
n
вершинами, длины ребер определяются по формуле (1), где
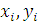 - координаты вершин. Найти остовное дерево минимальной длины. - координаты вершин. Найти остовное дерево минимальной длины.
В таком виде задача была поставлена и решена Примом (1961). Краскал, одновременно и независимо, поставил и решил задачу не для плоского случая, где расстояния определяются по формуле (1), а для произвольных положительных 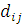 . При этом для некоторых пар индексов . При этом для некоторых пар индексов 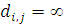 , что означает отсутствие ребра, т.е. рассматривается любой граф, а не только полный. , что означает отсутствие ребра, т.е. рассматривается любой граф, а не только полный.
Итак, вышеприведенный вариант есть, строго говоря, задача Прима, а задача Краскала
звучит так: Дан граф с
n
вершинами; длины ребер заданы матрицей
D
[
i
,
j
]. Найти остовное дерево минимальной длины
.
Обе перечисленные задачи решаются одним алгоритмом, причем алгоритмом самой примитивной разновидности.
Представим себе, что зимовщику оставлен некоторый запас продуктов, и его задачей является составление вкусного меню на всю зиму. Если зимовщик начнет с того, что сперва будет есть самую вкусную еду (например, шоколад), потом — вторую по вкусности (например, мясо), то он рискует оставить на последний месяц только соль и маргарин. Подобным образом, если оптимальный (для определенности, минимальный) объект строится как-то по шагам, то нельзя на первом шаге выбирать что-то самое малое, на втором шаге — оставшееся самое малое и т. д. За такую политику обычно приходится жестоко расплачиваться на последних шагах. Алгоритм, который мы привели, называется жадным.
В задаче Прима-Краскала жадный алгоритм дает точное оптимальное решение.
Как известно (это легко доказать, скажем, по индукции), дерево с nвершинами имеет n-1 ребер. Оказывается, каждое ребро надо выбирать жадно (лишь бы не возникали циклы).
(краткое описание)
1. В цикле
n
-1
раз делай: выбрать самое короткое еще не выбранное ребро при условии, что оно не образует цикла с уже выбранными.
Выбранные таким образом ребра образуют искомое остовное дерево.
Чтобы новое ребро не образовывало цикла со старыми, до построения дерева окрасим каждую вершину i в отличный от других цвет i. При выборе очередного ребра (x,y), где x и у имеют разные цвета, вершина у и все, окрашенные в ее цвет (т. е. ранее с ней соединенные) перекрашиваются в цвет x. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора n-1 ребер все вершины получают один цвет.
Итак, более подробный алгоритм выглядит так.
Алгоритм Прима-Краскала
1. Инициализируем граф - вводим матрицу весов графа D[i,j]
2. "Раскрашиваем" вершины графа в разные цвета
3. До тех пор, пока число ребер остова меньше числа вершин графа, выполняем:
1) Находим ребро минимальной длины, не включенное до этого в остов графа и не образующее цикла с остовом
2) Включаем найденное ребро минимальной длины в остов
3) Меняем цвет всех вершин, входящих в остов, на один цвет
Докажем, что описанный алгоритм получает в точности минимальное решение.
Для доказательства нам понадобится очень простое утверждение:
Если к дереву добавить ребро, то в дереве появится цикл, содержащий это ребро.
Действительно, пусть добавлено ребро (u, v) – «добавлено» означает, что ребро – новое, что раньше его в дереве не было. Поскольку дерево является связным графом, то существует цепь С(u, ..., v) из нескольких ребер, соединяющая вершины uи v. Добавление ребра (u, v) замыкает цепь, превращая ее в цикл.
Теорема.
Алгоритм Прима-Краскала получает минимальное остовное дерево.
Доказательство.
Результатом работы алгоритма является набор из n-1 ребер. Они не образуют цикла, ибо на каждом из n-1 шагов соединялись вершины разного цвета, т. е. ранее не связанные. Этот граф связный, потому что после проведения 1-го ребра осталось n-1 разных цветов, ..., после проведения (n-1)-го ребра остался один цвет, т. е. одна компонента связности. Итак, полученный набор ребер образует связный граф без циклов, содержащий n-1 ребер, т. е. n вершин. Следовательно, граф есть остовное дерево.
Осталось доказать, что оно имеет минимальную длину. Пусть {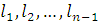 } ребра остовного дерева в том порядке, как их выбирал алгоритм, т. е. } ребра остовного дерева в том порядке, как их выбирал алгоритм, т. е. 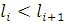 . Предположим для простоты доказательства, что все ребра сети имеют разную длину, т.е. . Предположим для простоты доказательства, что все ребра сети имеют разную длину, т.е.
 (2) (2)
Если полученное дерево не минимально, то существует другое дерево, задаваемое набором из n-1 ребер {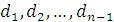 }, такое что сумма длин }, такое что сумма длин 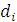 меньше суммы длин меньше суммы длин 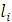 . С точностью до обозначений . С точностью до обозначений
 (3) (3)
Может быть,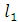 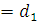 , , 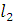 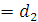 и т.д., но так как деревья разные, то в последовательностях (2) и (3) найдется место, где ребра отличаются. Пусть самое левое такое место – k, так что и т.д., но так как деревья разные, то в последовательностях (2) и (3) найдется место, где ребра отличаются. Пусть самое левое такое место – k, так что 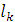 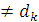 (kможет равняться единице, это не испортит доказательства). Поскольку (kможет равняться единице, это не испортит доказательства). Поскольку 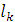 выбиралось по алгоритму самым малым из необразующих цикла с .ребрами выбиралось по алгоритму самым малым из необразующих цикла с .ребрами 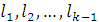 , то , то 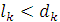 . Теперь добавим к дереву (3) ребро . Теперь добавим к дереву (3) ребро 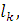 в нем появится цикл, содержащий ребро в нем появится цикл, содержащий ребро 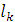 и, может быть, какие-то (или все) ребра из и, может быть, какие-то (или все) ребра из 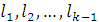 , но они сами не образуют цикла, поэтому в цикле будет обязательно ребро d
из набора , но они сами не образуют цикла, поэтому в цикле будет обязательно ребро d
из набора 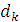 , причем , причем 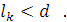 Выбросим из полученного графа с одним циклом ребро d
; мы снова получим дерево, но оно будет на Выбросим из полученного графа с одним циклом ребро d
; мы снова получим дерево, но оно будет на 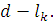 короче минимального, что невозможно. Полученное противоречие доказывает теорему для сети со всеми разными ребрами. короче минимального, что невозможно. Полученное противоречие доказывает теорему для сети со всеми разными ребрами.
Если не предполагать, что все ребра разные, то в доказательстве могло бы получиться, что 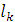 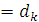 , и нам пришлось бы двигаться дальше по последовательностям (2) и (3), пока бы мы не нашли , и нам пришлось бы двигаться дальше по последовательностям (2) и (3), пока бы мы не нашли 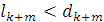 . Это усложняет доказательство, но не меняет заключения. . Это усложняет доказательство, но не меняет заключения.
В заключение анализа алгоритма оценим требуемую память и требуемое число операций. В варианте Прима надо хранить 2nкоординат точек, в варианте Краскала – n2
расстояний; в обоих вариантах удобно хранить 2(n-1) номеров вершин, т е. n-1 ребер ответа. Всего требуется памяти 0(n ), т.е. порядка n2
, что, учитывая реальные величины n, необременительно. Для нахождения текущего минимального ребра надо просмотреть 0(n2
) чисел и сделать это надо n-1 раз, так что временная сложность алгоритма 0(n3
). Это тоже реально. Задача Прима-Краскала относится к просто и точно решаемым.
Пример 1.
(вариант 17 контрольной работы по теме «Графы»)
Найти остовное дерево минимальной длины для графа, заданного следующей матрицей весов
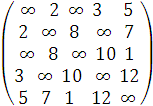
Решение.
Изобразим граф, заданный таблицей весов:

Воспользуемся алгоритмом Прима-Краскала (описание алгоритма на странице 14 курсового проекта).
1 шаг:
Раскрашиваем вершины графа в разные цвета:

2 шаг:
Находим ребро минимальной длины и включаем его в остов. Соединенные вершины остова перекрашиваем в один цвет:

3 шаг:
Находим следующее ребро минимальной длины, не входящее в остов, и включаем его в остов. Все вершины, связанные с ребром, перекрашиваем в один цвет:

4 шаг:
повторяем основной шаг:

5 шаг:
повторяем основной шаг:

Все вершины графа связаны ребрами – мы получили искомый остов. Его матрица весов имеет вид:
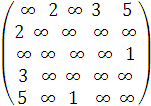
На этом примере была также протестирована реализация алгоритма Прима-Краскала на языке Паскаль, приведенная в Приложении. Результаты тестирования совпадают с полученным нами решением:

Примечание:
матрицу неориентированного графа достаточно задавать выше (ниже) ее главной диагонали.
Пример 2.
Найти остовное дерево минимальной длины для следующего графа:

Искомое остовное дерево:

Результаты тестирования программы, приведенной в Приложении:

Пример 3.
Случай вырожденного графа с пятью вершинами:

Заключение
Теория графов, будучи крупной ветвью комбинаторной математики, интенсивно изучалась в течение не одной сотни лет. Было выявлено много важных и полезных свойств графов, однако многие задачи еще ждут своего решения. Как и множество других предметных областей, которые приходилось изучать, алгоритмическое исследование графов возникло сравнительно недавно. И хотя некоторые фундаментальные алгоритмы открыты давно, все же большая часть интереснейших алгоритмов получена в течение нескольких последних десятилетий. Даже простейшие алгоритмы на графах позволяют получить полезные компьютерные программы, а нетривиальные алгоритмы относятся к числу наиболее элегантных и интересных из известных алгоритмов. Чтобы продемонстрировать все разнообразие приложений, использующих графы для обработки данных, рассмотрим нескольких примеров.
Географические карты.
Путешественник, прежде чем отправиться в путь, желает получить ответ на вопросы типа: "Какой маршрут из Принстона в Сан-Хосе потребует наименьших расходов?' Пассажир, для которого время дороже денег, хотел бы получить от- ответ на такой вопрос: "Каким путем быстрее всего добраться из Принстона в Сан-Хосе?" Чтобы ответить на вопросы подобного рода, мы выполняем обработку информации, характеризующей соединения (пути следования) между элементами (городами и населенными пунктами).
Гипертекст.
Когда мы просматриваем Web-каталоги, мы сталкиваемся с документами, содержащими различные ссылки (соединения) на другие документы, и переходим от документа к документу, щелкая мышью на этих ссылках. Сама по себе "всемирная паутина" представляет собой граф, в котором в качестве элементов выступают документы, а соединения суть связи. Алгоритмы обработки графов являются важными компонентами поисковых механизмов, которые помогают определить местоположение информации в Web.
Микросхемы.
Микросхемы содержат такие элементы, как транзисторы, резисторы, конденсаторы, которые связаны между собой сложнейшим образом. Для управления машинами, изготавливающими микросхемы, и для проверки, выполняют ли эти цепи заданные функции, используются компьютеры. Мы хотим получить ответы на простые вопросы наподобие "Имеются ли в цепи условия для короткого замыкания?" и на более сложные вопросы, такие как "Можно ли скомпоновать микросхему на кристалле таким образом, чтобы шины не пересекались?". В данном случае, ответ на первый вопрос зависит только от свойств соединений (шин), в то время как для ответа на второй вопрос потребуется подробная информация о шинах, элементах, которые эти шины соединяют, и физических ограничениях, накладываемых кристаллом.
Составление расписаний.
Производственный процесс требует решения различных задач под воздействием некоторого множества ограничений, по условиям которых решение одной задачи не может быть начато до тех пор, пока не будет завершено решение другой задачи. Мы представляем эти ограничения в виде соединений между этими задачами (элементами), при этом перед нами возникает задача составления расписаний (scheduling) в ее классическом виде: как построить временной график решения задач таким образом, чтобы удовлетворить заданным ограничениям и завершить данный процесс за минимально возможное время?
Транзакции.
Телефонная компания поддерживает базу данных телефонного трафика. В этом случае соединения представляют телефонные вызовы. Мы заинтересованы в том, чтобы знать все, что касается характера структуры соединений, ибо хотим проложить провода и установить коммутаторы так, чтобы эффективно справляться с телефонным трафиком.
Еще одним примером может служить то, как финансовое учреждение отслеживает операции купли/продажи на рынке. Соединение в рассматриваемом случае представляет собой передачу денег продавцом покупателю. Знание свойств структуры соединений в данном случае помогает лучше понять особенности рынка.
Задачи поиска сочетаний.
Студенты обращаются с заявлениями на замещение должностей в таких общественных организациях, как общественные клубы, университеты или высшие медицинские учебные заведения. Элементы соответствуют студентам и институтам, тогда как связи соответствуют приложениям. Мы хотим найти методы, устанавливающие соответствие между вакантными должностями и заинтересованными в их получении студентами.
Сети.
Сеть вычислительных машин состоит из взаимосвязанных узлов, которые посылают, передают дальше и получают сообщения различных видов. Мы заинтересованы не только в обеспечении возможности получать сообщения из любого другого узла, но и в том, чтобы эта возможность сохранялась для всех пар узлов и в случае изменения конфигурации сети. Например, возможно, потребуется проверить работу конкретной сети, чтобы убедиться в отсутствии некоторого небольшого подмножества узлов или соединений, настолько критичного для работы всей сети, что его утрата может привести к разъединению остальных пар узлов.
Структура программы.
Компилятор строит графы для представления структуры вызовов крупной системы программного обеспечения. Элементами в этом случае являются различные функции или программные модули, составляющие систему; соединения отождествляются либо с возможностью того, что одна функция может вызвать другую функцию (статический анализ), или с фактическим вызовом, когда система находится в рабочем состоянии (динамический анализ). Нам нужно выполнить анализ графа, чтобы определить, как достичь максимальной эффективности при выделении системных ресурсов для конкретной программы.
Эти примеры демонстрируют, насколько широк диапазон приложений, для которых граф служит подходящей абстракцией, и, соответственно, диапазон вычислительных задач, с которыми доведется столкнуться при работе с графами.
Модели графов, в которых с каждым ребром связывают веса или стоимости, используются во многих приложениях. В картах авиалиний, в которых ребрами отмечены авиарейсы, такие веса означают расстояния или стоимость проезда. В электронных схемах, где ребра представляют электрические соединения, веса могут означать длину соединения, его стоимость или время, необходимое для распространения по ней сигнала. В задачах календарного планирования веса могут представлять время или расходы, затрачиваемые на выполнение задач, либо время ожидания завершения соответствующей задачи. Естественно, в таких ситуациях возникают вопросы, касающиеся различных аспектов минимизации стоимости. Наиболее изучены алгоритмы решения двух задач такого рода:
1) Определение пути с наименьшей стоимостью, соединяющего все точки;
2) Отыскание пути наименьшей стоимости, соединяющего две заданных точки.
Первый тип алгоритма применяется для решения задач на неориентированных графах, которые представляют такие объекты как электрические цепи, находит минимальное остовное дерево
. Второй тип алгоритма, применяемый для решения задач на орграфах, которые представляют такие объекты, как карты авиарейсов, определяет кратчайшие пути
. Эти алгоритмы находят широкое применение не только в приложениях, связанных со схемами авиарейсов и электрическими схемами, они используются также и при решении задач, возникающих во взвешенных графах.
Задача поиска минимального остовного дерева произвольного взвешенного неориентированного графа получила множество важных применений, и алгоритмы ее решения были известны, по меньшей мере, с двадцатых годов прошлого столетия. Тем не менее, эффективность ее реализации колеблется в широких пределах, а исследователи до сих пор заняты поисками более совершенных методов.
Литература
1. Кpистофидес, H. Теоpия гpафов. Алгоритмический подход. М. "Миp", 1978
2. Бондарев В.М., Рублинецкий В.И., Качко Е.Г. Основы программирования / Харьков: Фолио; Ростов на Дону: Феникс, 1997. – 368 .
3. Захарова, Л.Е. Алгоритмы дискретной математики: учебное пособие. – Моск. гос. ин-т электроники и математики. М., 2002, 120 с.
4. Кормен Т. Х., Лейзерсон Ч. И., Ривест Р. Л., Штайн К. Алгоритмы: построение и анализ, 2-е изд. — М.: Вильямс, 2005. — 1296 с.
5. Седжвик, Роберт Фундаментальные алгоритмы на C++. Алгоритмы на графах: Пер. с англ./ Роберт Седжвик. - СПб: ООО «ДиаСофтЮП», 2002. - 496 с.
6. http://www.algolist.manual.ru/links/
7. http://www.devel.vcity.ru/library.tmpl?05344_article_id=8
8. http://www.ergeal.ru/txt/archive/cs/discra/index.htm
9. Hечепуpенко, М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях. – Hовосибиpск: Hаука, 1990
10. Алгоритм Флойда-Уоршелла // [Электронный ресурс]: Энциклопедия Википедия. – Электрон. дан. – Режим доступа: http://ru.wikipedia.org/wiki/Алгоритм_Флойда_—_Уоршелла. – Загл. с экрана.
11. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: Бином, 2000. – 960с.
12. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.
13. Липский В. Комбинаторика для программистов: Пер. с польск. – М.: Мир, 1988. – 213 с.
14. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2004. – 368с.
15. Оре О. Теория графов. – М.: Наука, 1980.
Приложение
Реализация алгоритма Прима-Краскала на языке Паскаль
useswincrt;
Const
N=5; {N - число вершин графа}
type
Matrix=array[1..N,1..N] of Integer; {матрицарасстоянийграфа}
var
D,Ostov: Matrix; {D - матрица весов исходного графа, Ostov - матрица весов искомого остова}
color_of_top: array[1..N] of integer; {цветвершинграфа}
i,j,k,x,y,d_min: Integer; {d_min - текущая минимальная длина ребра}
ne_virozhd: Boolean;
BEGIN
ClrScr;
{Инициализируем граф - вводим матрицу весов графа D[i,j]}
for i:=1 to N do begin
WriteLn('Введите элементы ',i,'-й строки матрицы весов графа:');
WriteLn('Если вершины не связаны ребром - вводим любое отрицательное число');
for j:=1 to N do begin
Write('D[',i,',',j,']='); Read(D[i,j]);
end;
end;
{Выводим матрицу весов графа D[i,j]}
WriteLn;
WriteLn('Матрица весов графа:');
for i:=1 to N do begin
for j:=1 to N do begin
If D[i,j]>=0 then Write(D[i,j]:5) else Write(' x');
end;
WriteLn;
end;
{Инициализируем матрицу остовного дерева графа}
for i:=1 to N do
for j:=1 to N do
Ostov[i,j]:=0;
{"Раскрашиваем" вершины графа в разные цвета}
for i:=1 to N do
color_of_top[i]:=i;
k:=0; {k - число ребер остовного дерева}
ne_virozhd:=false;
{Общий шаг алгоритма}
whilek<N-1 dobegin
{Задаем первоначальное значение длины искомого ребра, заведомо большее всех имеющихся у графа}
d_min:= 30000;
{Находим ребро минимальной длины, не включенное до этого в остов графа}
for i:=1 to N-1 do
for j:=i+1 to N do
if (i<>j)and(D[i,j]>0) and (D[i,j]<d_min) and (color_of_top[i]<>color_of_top[j]) then
begin
d_min:=D[i,j];
x:=i;
y:=j;
ne_virozhd:=true;
end;
if ne_virozhd=true then begin
{Включаем найденное ребро минимальной длины в остов}
Ostov[x,y]:=D[x,y];
{Меняем цвет всех вершин, входящих в остов, на один цвет}
for i:=1 to N do
if color_of_top[i] = y then color_of_top[i] := x;
end;
{Увеличиваем количество рассмотренных ребер}
k:=k+1;
end;
{Выводим матрицу весов остова}
WriteLn;
WriteLn('Искомая матрица весов остова:');
for i:=1 to N do begin
for j:=1 to N do begin
If Ostov[i,j]>0 then Write(Ostov[i,j]:5) else Write(' x');
end;
WriteLn;
end;
END.
2. Блок
-схема алгоритма

|