1.Задача № 1
По данным эксплуатационных и ремонтных служб вероятность выхода из строя ТЭД в депо, эксплуатирующем электровозы, за одну поездку составляет р = 0,15.
Определить методом перебора и проверить по максимуму функции распределения наиболее вероятное количество ТЭД, выходящих из строя в месяц, если известно, что за этот период электровоз делает в среднем n = 14 поездок.
Решение:
Согласно схеме биномиальных испытаний, вероятность того, что в n испытаниях выйдет из строя k ТЭД запишется в виде:
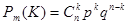 , (1.1) , (1.1)
Где 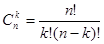 (1.2) (1.2)
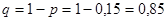 (1.3) (1.3)
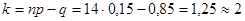 (1.4) (1.4)
То есть из 14 поездок выйдет из строя 2 ТЭД.
При k = 1:
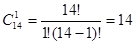 ; ;
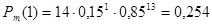 ; ;
При k = 2:
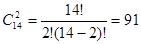 ; ;
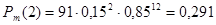
При k = 3:
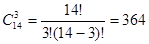 ; ;
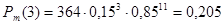
Как видно, при k = 3 вероятность Р начинает убывать, поэтому количество двигателей, которые могут выйти из строя принимаем равное 2.
Вывод: определили наибольшую вероятность р = 0,291 выхода из строя определенного числа ТЭД k = 2.
2.Задача № 2
Изменяются нижеследующие данные по эксплуатации ТЭД в период послегарантийного пробега локомотива. При этом известно, что в период гарантийного пробега (350000 км) ТЭД из строя не выходили. Данные приведены в таблице 2.1.
Принимая закон распределения вероятностей отказов ТЭД экспоненциальным (пробег близок к гарантийному), определить:
1. Вероятность того, что за пробег L тыс.км отказов ТЭД на локомотиве не будет.
2. Вероятность того, что ТЭД на локомотиве придется менять точно 3 раза.
3. Вероятность того, что ТЭД придется менять не менее 3 раз.
4. Сколько ТЭД на локомотиве выйдет из строя за пробег Lтыс. км.
Таблица 2.1
Пробеги ТЭД до отказа
Условные
Номера ТЭД
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Пробег, тыс. км |
385 |
435 |
485 |
395 |
455 |
595 |
735 |
635 |
745 |
645 |
| Условные номера ТЭД |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| Пробег, тыс. км |
560 |
445 |
535 |
670 |
740 |
430 |
451 |
418 |
405 |
705 |
Заданный пробег локомотива – L = 564 тыс. км.
Решение:
Вероятность отказа не зависят от времени предшествующей работы, а зависит только от длины интервала, надежность элемента может быть рассчитана на основе экспоненциального закона распределения вероятностей.
1.В соответствии с этим законом вероятность безотказной работы ТЭД при пробеге L тыс. км может быть вычислена по формуле:
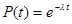 (2.1) (2.1)
Где 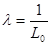 (2.2) (2.2)
Где, в свою очередь 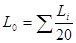 (2.3) (2.3)
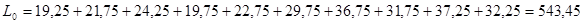 (км) (км)
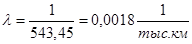
Вероятность безотказной работы при пробеге Lтыс. км:
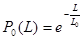 (2.4) (2.4)
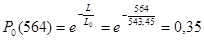 . .
2.Вероятность того, что ТЭД на электровозе придется менять точно 3 раза:
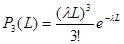 (2.5) (2.5)
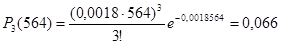
3.Вероятность того, что ТЭД придется менять не менее 3-х раз:
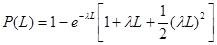 (2.6) (2.6)
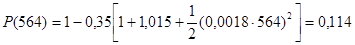
4.Вопрос, сколько ТЭД на локомотиве выйдет из строя за пробег 564 тыс.км, решаем путем перебора вариантов с использованием формулы:
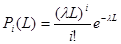 (2.7) (2.7)
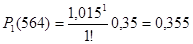
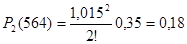
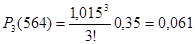

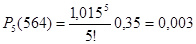
В результате расчетов получаем, что количество ТЭД, которое выйдет из строя равно 4 ТЭД.
3. Задача №3
Пусть средний пробег локомотива по депо за год составляет 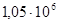 тыс. км. В поездках происходит n = 8 отказов двигателей из-за размотки бандажей. По результатам обследования выясняется, что во всех случаях размотки произошли вследствие разносного боксования ТЭД. тыс. км. В поездках происходит n = 8 отказов двигателей из-за размотки бандажей. По результатам обследования выясняется, что во всех случаях размотки произошли вследствие разносного боксования ТЭД.
Определить вероятность того, что в депо за общий пробег локомотива L = 564 тыс. км отказов ТЭД по якорным бандажам не произойдет. Плечи обращения локомотивных бригад составляют по всем направлениям 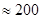 км. Локомотивы 4-осные. км. Локомотивы 4-осные.
Решение:
Вероятность отказа ТЭД из-за размотки бандажей в одной поездке, может быть вычислена как частость отказа:
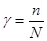 , (3.1) , (3.1)
Где N – количество двигателей, участвующих в поездках локомотива за год, определяемое из заданного среднего пробега и заданных плеч обращения локомотивов
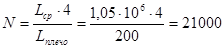 ТЭД (3.2) ТЭД (3.2)
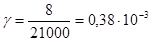
Вычислим количество поездок:
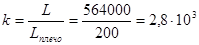 поездок (3.3) поездок (3.3)
Вычислим произведение 
Так как величина 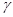 мала, k – велико, произведение мала, k – велико, произведение 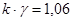 и находится в пределах 0,1-20, то вероятность безотказной работы ТЭД за время и находится в пределах 0,1-20, то вероятность безотказной работы ТЭД за время 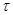 большее числа поездок kвычислим по формуле: большее числа поездок kвычислим по формуле:
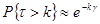 (3.4) (3.4)
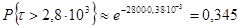
Вывод: в ходе выполнения данной задачи определили вероятность того, что в депо за общий пробег локомотива отказов ТЭД по якорным бандажам не произойдет, р = 0,345.
4.Задача №4
Пусть имеются данные о времени безотказной работы моторно-якорных подшипников (таблица 4.1)
Таблица 4.1
Данные по отказам моторно-якорных подшипников
| Условные номера подшипников |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| Пробег до отказа, тыс.км |
385 |
435 |
485 |
345 |
455 |
595 |
735 |
635 |
785 |
745 |
645 |
| Условные номера подшипников |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
| Пробег до отказа, тыс.км |
560 |
435 |
535 |
635 |
735 |
785 |
795 |
800 |
805 |
810 |
815 |
Определить вероятность безотказной работы за L тыс. км.
Предполагается, что опасность отказа 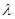 при эксплуатации локомотива остается постоянной. Пробег L = 564 тыс. км. при эксплуатации локомотива остается постоянной. Пробег L = 564 тыс. км.
Решение:
1.Примем значение 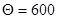 тыс.км; тыс.км;
2.Определим функцию 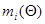 - число отказов до пробега 600 тыс. км, - число отказов до пробега 600 тыс. км, 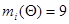
3.Определим накопленную частость отказов:
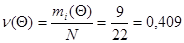 (4.1) (4.1)
4.Опрделим опасность отказов:
Так как 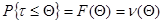 (4.2) (4.2)
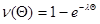 (4.3) (4.3)
Откуда 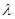 будет равна: будет равна:
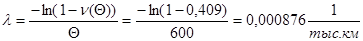 (4.4) (4.4)
5.Вероятность безотказной работы за 564 тыс. км:
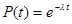 (4.5) (4.5)
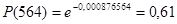
6.Вероятность отказа за тот же пробег:
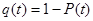 (4.6) (4.6)
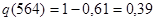
Вывод: в ходе выполнения данной задачи, определили вероятность безотказной работы за пробег L = 564 тыс. км, которая составила р = 0,61.
5.Задача №5
Определить параметры распределения и оценить вероятность безотказной работы подшипников в течение времени 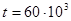 часов и часов и 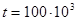 часов. часов.
Данные о работе моторно-якорных подшипников приведены в таблице 5.1.
Таблица 5.1
Время безотказной работы моторно-якорных подшипников
| Услов. номер подшипника |
Время безотказной работы.; 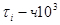 |
Услов. номер подшипника |
Время безотказной работы.; 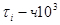 |
Услов. номер подшипника |
Время безотказной работы.; 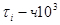 |
Услов. номер подшипника |
Время безотказной работы.; 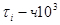 |
Услов. номер подшипника |
Время безотказной работы.; 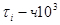 |
| 1 |
24 |
11 |
54 |
21 |
66 |
31 |
75 |
41 |
87,5 |
| 2 |
27,5 |
12 |
55 |
22 |
68,5 |
32 |
76 |
42 |
92,5 |
| 3 |
36 |
13 |
56 |
23 |
70 |
33 |
76,5 |
43 |
96 |
| 4 |
41,5 |
14 |
57,5 |
24 |
71 |
34 |
77 |
44 |
97,5 |
| 5 |
42,5 |
15 |
28 |
25 |
71 |
35 |
78 |
45 |
105 |
| 6 |
46 |
16 |
60 |
26 |
71,5 |
36 |
79,5 |
46 |
111 |
| 7 |
47,5 |
17 |
61 |
27 |
72,5 |
37 |
80 |
47 |
116,5 |
| 8 |
49 |
18 |
62,5 |
28 |
73 |
38 |
82,5 |
48 |
132,5 |
| 9 |
51 |
19 |
63 |
29 |
74 |
39 |
83,5 |
49 |
142,5 |
| 10 |
51,5 |
20 |
65 |
30 |
74 |
40 |
80 |
50 |
145 |
Решение:
1.Найдем эмпирическое среднее и дисперсию времени безотказной работы:
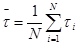 (5.1) (5.1)
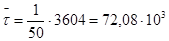 (ч) (ч)
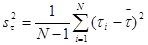 (5.2) (5.2)
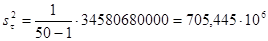 час2 час2
2.Определим опасность отказов 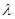 и число повреждений r: и число повреждений r:
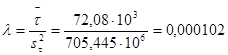 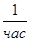 (5.3) (5.3)
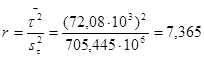 (5.4) (5.4)
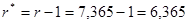
3.Определим произведения 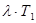 и и 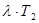 : :
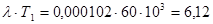
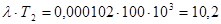
4.По номограмме для определения вероятностей безотказной работы, взятой из источника [2], определяем функции 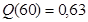 и и 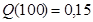
5.Используя нормальное распределение, запишем:
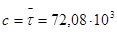 час (5.5) час (5.5)
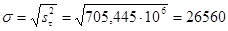
6.Посчитаем аргументы функции Лапласа:
 (5.6) (5.6)
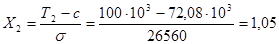 (5.7) (5.7)
7. По таблице функции Лапласа, взятой из источника [2], определяем
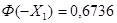
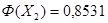
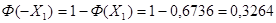
8. Запишем вероятность безотказной работы при нормальном законе распределения:
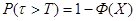 (5.8) (5.8)
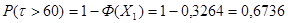
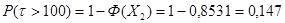
Вывод: в ходе решения данной задачи определили параметры распределения и оценили вероятность безотказной работы подшипников, 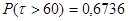 и и 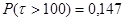 . .
6.Задача №6
На ресурсные испытания корпусной изоляции якорей ТЭД ЭД118А были поставлены 1461 образец. По результатам испытаний была получена следующая таблица, характеризующая их надежность.
Таблица 6.1
Результаты наблюдений и исходные данные для расчета
характеристик надежности ТЭД ЭД118А
Интервалы
наработки
|
Показатели надежности |
| Центр интервала t, тыс.км |
Число работоспособных ТЭД в интервале N(t),штук |
Число отказов в момент наработки t, ni
штук |
| 0 |
0 |
1461 |
0 |
| 1 |
50 |
1444 |
17 |
| 2 |
150 |
1401 |
43 |
| 3 |
250 |
1328 |
73 |
| 4 |
350 |
1224 |
104 |
| 5 |
450 |
1060 |
164 |
| 6 |
550 |
859 |
201 |
| 7 |
650 |
621 |
238 |
| 8 |
750 |
431 |
190 |
| 9 |
850 |
252 |
179 |
| 10 |
950 |
132 |
120 |
| 11 |
1050 |
69 |
63 |
| 12 |
1150 |
31 |
38 |
| 13 |
1250 |
8 |
23 |
Используя данные таблицы 6.1, рассчитать количество запасных ТЭД, которыми должно располагать эксплуатационное предприятие для случаев их замены под локомотивами в данном регионе использования на среднюю наработку локомотивов по депо в 15 000 тыс. км с заданной вероятностью обеспечения замены Р = 0,99.
Решение:
Требуемое количество ремонтов якорей ТЭД n0
в электромашинном цехе депо за период эксплуатации t или число якорей ТЭД, которое должно быть на складе для их замены на локомотивах взамен вышедших из строя, равно:
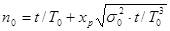 (6.1) (6.1)
Где хр
– квантиль порядка Р нормального распределения, определяемого из условия Ф(хр
)=Р;
Т0
– математическое ожидание времени безотказной работы корпусной изоляции якорей ТЭД. Рассчитывается как статистическое значение среднего времени безотказной работы с использованием данных таблицы 6.1 по формуле:
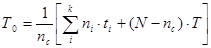 (6.2)
(6.2)
Где 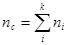 - общее число отказавших ТЭД; - общее число отказавших ТЭД;
k – общее число моментов наработки (число интервалов наработки);
i – 1,2,…..,k – индекс наработки ТЭД в момент отказа;
ni
– число отказов в момент наработки ti
;
ti
– момент наработки возникновения отказа (центр интервала наработки);
N – продолжительность наблюдений.
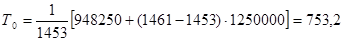 тыс. км
тыс. км
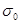 - среднее квадратичное отклонение наработки ТЭД от среднего значения: - среднее квадратичное отклонение наработки ТЭД от среднего значения:
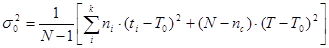 (6.3) (6.3)
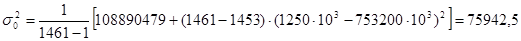
Далее, используя полученные данные и формулу (6.1), можно рассчитать для заданных условий задачи количество запасных ТЭД, которыми должно располагать эксплуатационное предприятие в данном регионе эксплуатации локомотивов:
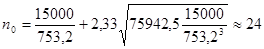 ТЭД ТЭД
Вывод: в ходе решения данной задачи, рассчитали количество запасных ТЭД, которыми должно располагать эксплуатационное предприятие для случаев их замены под локомотивами в данном регионе использования на среднюю наработку локомотивов по депо в 15 000 тыс. км с заданной вероятностью обеспечения замены Р = 0,99, nо
= 24 ТЭД.
|