Реферат: Эллипсометрия как метод неразрушающего контроля

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра ЭТТ

РЕФЕРАТ

На тему:

«Эллипсометрия, как метод неразрушающего контроля»

МИНСК, 2008

Эллипсометрия - метод неразрушающего контроля состояния поверхности полупроводниковых пластин, параметров тонких поверхностных слоёв и границ раздела между ними, основанный на анализе изменения поляризации пучка поляризованного монохроматического света при его отражении от исследуемого объекта. Т.к. обычно измеряются параметры эллиптически поляризованного света, метод назван эллипсометрическим или просто эллипсометрией.

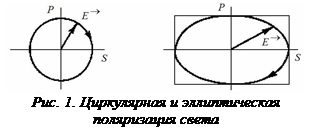
Поляризация света. Свет со всевозможными одинаково вероятностными колебаниями электрического вектора называется естественным светом. Если вектор электрического поля в процессе колебаний устойчиво изменяет свою ориентацию, то может иметь место либо циркулярная поляризация, либо эллиптическая поляризация. В первом случае конец вектора описывает в пространстве окружность, а во втором - эллипс (рис. 1). В отражённом от кристалла под некоторым углом, называемом углом Брюстера, свете колебания электрического вектора происходят преимущественно в одном направлении. Такой свет называется линейно или плоскополяризованным. Рассмотрим это более подробно. Предположим, что монохроматическая волна оптического излучения падает на идеально гладкую поверхность исследуемой изотропной плёнки под углом  к нормали. Эта волна частично отражается от поверхности плёнки под углом ’, равным углу падения , а частично будет распространяться в глубь плёнки под углом преломления  (рис. 2,а). Как известно, соотношение между углом падения и углом преломления определяется следующим законом:

sin/sin = n1/n2 = n21 ,

где n1 и n2 - соответственно показатель преломления первой и второй оптической среды по ходу распространения волны.

Рис. 2. Линейная поляризация света при отражении и преломлении света от раздела двух диэлектрических сред

Взаимодействие электромагнитного поля с немагнитными средами определяется в основном его электрической составляющей Е, которую можно разложить на две компоненты, поляризованные во взаимно перпендикулярных плоскостях:

Е= еpEpcosp + еsEscoss ,

где еp , еs - единичные векторы поляризации, Ep, Es - амплитуды p- и s-составляющих вектор Е, p,s - фазы колебаний p- и s-составляющих.

При этом s-компонентой обозначается составляющая электрического вектора, колеблющаяся в плоскости, перпендикулярной плоскости падения излучения, а p-компонентой - составляющая, параллельная плоскости падения.

Соотношение между амплитудами s- и p-компонент электрического вектора Е для отражённой Е и преломлённой Еnp волн и соответствующими компонентами падающей волны Еnp определяется формулами Френеля:

Еp = Еnp tg(-)/tg(+);

Еs = -Еns sin(-)/sin(+);

Еnpp = Еnp 2sinsin/sin(+)cos(-);

Еnps = Еns 2sincos/sin(+).

Анализ формул Френеля показывает, что при некоторых соотношениях углов  и  отраженный и преломленный лучи будут частично и даже полностью поляризованы. Так, если угол падения удовлетворяет условию +/2, что соответствует tg = n21, то p-компонента отражённой волны равняется нулю и отражённый пучок света оказывается полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом угол  называется углом Брюстера - Бр (рис.2,б).

Рис. 3. Линейная и циркулярная поляризация при двойном лучепреломлении

Эллиптически- и циркулярно-поляризованный свет можно получить из линейно-поляризованного. Для этого нужно сдвинуть фазы колебаний s- и p-составляющих линейно-поляризованного пучка света друг относительно друга. Сдвиг фаз между p- и s-волнами можно осуществить с помощью пластинки из двухлучепреломляющего кристалла (исландский шпат, турмалин), в котором эти волны распространяются с различными скоростями (это определяет различный коэффициент преломления для p- и s-составляющих - np и ns ). При боковом падении линейно-поляризованного луча света на пластинку из двухлучепреломляющего кристалла из неё будут выходить два луча, поляризованных во взаимно перпендикулярных направлениях (рис. 3,а). При нормальном падении луча света выходные лучи будут иметь общую точку выхода из пластинки (рис. 3,б). Фазы колебаний этих лучей будут сдвинуты пропорционально оптической разности хода лучей в пластинке:

 = 2tp - 2ts = 2cd/vp - 2cd/vs =

= 2npd/ - 2nsd/ = (2/)(np - ns)d .

При  = /2 оптическая разность хода p- и s-лучей равна четверти длины волны падающего монохроматического пучка

(np - ns)d = /4 .

Такая пластинка называется четвертьволновой. Из этой пластинки линейно-поляризованный луч выходит эллиптически-поляризованным.

Для иллюстрации изменения вида поляризации при различном сдвиге фаз между p- и s-волнами на рис. 4 - 8 представлены диаграммы колебания вектора электрического поля. Из этих диаграмм видно, что изменение ориентации и формы эллипса зависит от изменения разности фаз p- и s-составляющих электрического вектора поляризованного пучка света, прошедшего либо отражённого от исследуемого образца. Это свойство эллиптически-поляризованного света и лежит в основе эллипсометрического метода контроля оптических констант, электрофизических параметров и толщины различных диэлектрических и полупроводниковых тонкоплёночных структур.

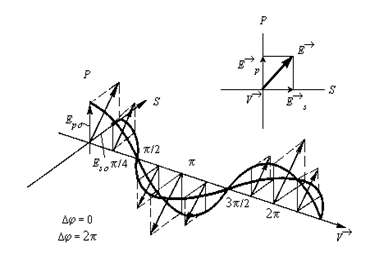
Рис. 4. Линейная поляризация света ( = 0)

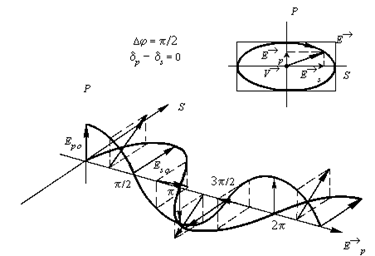
Рис. 5. Эллиптическая поляризация ( = /2)

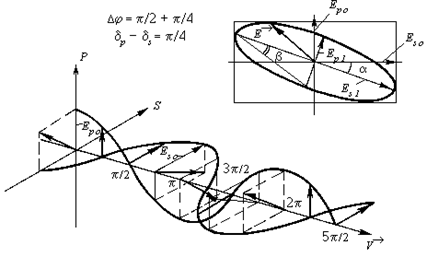
Рис. 6. Эллиптическая поляризация ( = 3/4)

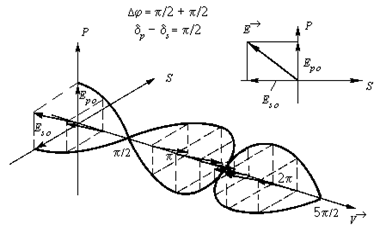
Рис. 7. Линейная поляризация ( = )

Рис. 8. Изменение поляризации света при изменении разности фаз между p- и s-составляющими от 0 до 2

Эллипсометрический метод контроля тонкоплёночных структур. Для однородной монохроматической плоской волны состояние поляризации может быть определено с помощью двух угловых величин: эллиптической разностью фаз  между s- и p-составляющими электрического вектора отражённой волны и азимутом  восстановленной линейной поляризации:

 = arctg¦rp¦/¦rs¦ = arctg(tg/tgn),

 =  - /2

где rp = Еp /Епp , rs = Еs /Еns - коэффициенты отражения p- и s-волны (в общем случае, величины комплексные);   и  п - углы, характеризующие форму эллипса для падающей и отражённой волны.

Разность фаз  характеризует угол разворота осей эллипса - , а азимут  - форму эллипса (соотношение осей через угол ).

Если ввести относительный коэффициент отражения , представляющий собой отношение комплексных коэффициентов отражения для p- и s-компонентов, то компонентов, то можно записать основное уравнение эллипсометрии, связывающее воедино отражающие свойства границы раздела с эллипсометрическими параметрами  и :

 = (¦rp¦/¦rs¦)еxp(i) = tg еi .

К числу основных особенностей эллипсометрии, затрудняющей её применение, относится то, что функциональная связь между непосредственно измеряемыми величинами и величинами, которые интересуют экспериментатора, является в большинстве случаев весьма сложной и нелинейной:

rp, rs  f (О, nО, kО, n, k, nj, kj, dj),

где О - угол падения; nО, kО - оптические константы внешней среды; n, k - оптические константы подложки; nj, kj - оптические константы слоёв; dj - толщины слоёв;

n, k  f (N, , rО, m*, tr),

где N - концентрация свободных носителей заряда;  - подвижность носителей заряда; r_О - удельное сопротивление; m* - эффективная масса; tr -время релаксации.

Задача исследователя - найти точное соответствие между интересующими его физическими величинами, например значениями толщин и показателями преломления плёнки на известной подложке и величинами измеряемых углов  и , т.е. определить искомые параметры образца.

При установлении количественной взаимосвязи между поляризационными углами и физическими параметрами отражающей системы существует две задачи: прямая - расчёт совокупности углов и  по известным параметрам этой системы, и обратная - вычисление конкретных значений физических величин, например, оптических констант и толщин слоёв, реальной структуры по измеренным по ней экспериментальным значениям поляризационных углов.

Наиболее перспективный и экспрессный путь получения информации - непосредственное решение обратной задачи на основе эллипсометрического уравнения. Но он требует встроенной в эллипсометр специализированной ЭВМ с довольно сложным программным обеспечением. Обычно же предварительно с помощью универсальной ЭВМ решают прямую задачу, т.е. для конкретной эквивалентной модели исследуемой тонкоплёночной структуры рассчитывают теоретические значения углов и  для всех возможных численных наборов реальных значений искомых физических величин. Таким образом проводят как бы градуировку эллипсометра. Затем, используя результаты решения прямой задачи, непосредственно при контроле тонкоплёночной структуры, решают обратную задачу. Наиболее просто прямая задача решается в случае, если в процессе измерения некоторого объекта имеется только два неизвестных параметра, относительно которых осуществляется расчёт.

Результат расчёта (т.е. решения прямой задачи) представляется в виде таблиц или а -, -номограмм (рис. 9). Решая затем обратную задачу искомые физические величины определяются путём сравнения экспериментально измеренных значений эллипсометрических углов с теоретическими зависимостями, например от n и d, т.е. с результатами решения прямой задачи. За одно измерение на эллипсометре определяются оба угла и  и, следовательно, два любых неизвестных физических параметра исследуемой системы, входящих в уравнение эллипсометрии, при известных остальных величинах.

Рис. 9. -,- номограмма для системы "прозрачная пленка – арсенид галлия"

Конструкции и функциональные схемы эллипсометров. Высокая точность измерений (погрешность измерений толщины 0,3нм) на плёнке SiO₂ , малая чувствительность к внешним воздействиям, отсутствие разрушающего воздействия - все эти важные преимущества эллипсометрического метода в сочетании с ЭВМ ставят его в ряд наиболее перспективных для технологического контроля (в реальном масштабе времени) не только толщин плёнок, но и оптических констант, диэлектрической проницаемости, концентрации и подвижности заряженных частиц, шероховатости поверхности и других параметров.

По способу измерения эллипсометрических параметров и эллипсометры могут быть разделены на две большие группы: ненулевые эллипсометры прямого фотометрирования и компенсационные нульэллипсометры (рис. 10). В эллипсометрах первой группы параметры  и  непосредственно не измеряются, а рассчитываются на основании данных об интенсивности излучения, отражённого от объекта измерений при заданных значениях азимутов поляризатора и анализатора. В компенсационных нульэллипсометрах, напротив, в результате измерений фиксируются угловые величины: азимуты анализатора tg  и поляризатора tg n, а также разность фаз , создаваемая компенсатором за счёт изменения его толщины d до получения минимальной (нулевой) интенсивности на выходе эллипсометра. Параметры и  в данном случае рассчитываются простыми соотношениями:

 = arctg(tg/tgn) ,

 = (2/)(np-ns)d - /2 .

функциональная схема ненулевого эллипсометра прямого фотометрирования. Оптическое излучение от лазера модулируется по амплитуде и, пройдя поляризатор с фиксированным азимутом, отражается от кремниевой пластины, на которую производится осаждение плёнки SiO₂ . Отражённое образцом лазерное излучение выходит из технологической камеры через оптическое окно и, попадая в приёмный блок, расщепляется с помощью двух светоделителей на три луча, которые проходят соответствующие анализаторы с углами поворота осей линейной поляризации (т.е. наибольшего пропускания) 0^о , 45^о и 90^о относительно плоскости падения излучения на образец и регистрируются фотодетекторами ФД1-ФД3. Электрические сигналы с фотодетекторов поступают на усилители А1-А3 и в блок записи и обработки информации, в котором по трём значениям интенсивности I₁ , I₂ и I₃ на выходе трёх анализаторов рассчитываются параметры и .

Наибольшее число отечественных эллипсометров строится по компенсационной схеме. Это обусловлено независимостью результата измерений от колебаний Методика измерений на эллипсометре компенсационного типа заключается в гашении отражённого от исследуемого образца луча на выходе эллипсометра посредством вращения вокруг оптической оси прибора двух из трёх установленных на лимбах оптических элементов (поляризатора, анализатора и компенсатора) и расчете параметров и  по углам поворота (азимутам) этих элементов относительно плоскости падения в положении гашения.

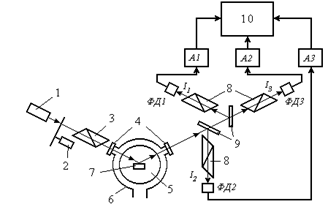
Рис. 11. Эллипсометр прямого фотометрирования для исследования нестационарных процессов:

1 - Не-Nе лазер; 2 - электромеханический модулятор; 3 - поляризатор; 4 - оптические окна; 5 - кварцевый реактор; 6 - индуктор; 7 - графитовый пьедестал с образцом; 8 - анализаторы; 9 - светоделители; 10 - блок обработки и записи информации

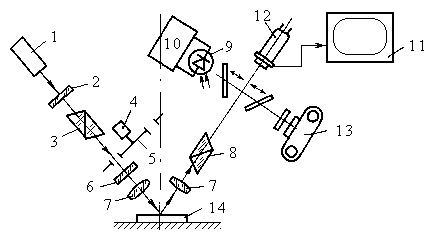
Рис. 12. Оптическая схема эллипсометрического микроскопа ЛЭМ-3:

1 - Не-Nе лазер; 2 - четвертьволновая пластина; 3 - поляризатор; 4 - электродвигатель; 5 - модулятор: 6 - компенсатор (четвертволновая пластина); 7 - объективы; 8 - анализатор; 9 - фотоэлемент; 10 - электронный блок; 11 - ВКУ; 12 - видикон; 13 - фотоаппарат; 14 - исследуемый образец

При получении с помощью системы эллипсометрических изображений гасятся только составляющие пучки света, отраженные от участков исследуемого образца, имеющих одинаковые параметры. Это позволяет оценить равномерность распределения контролируемых параметров (например, толщины плёнки) в исследуемых структурах (рис. 12). Соответствующие участки эллипсометрического изображения на экране выглядят темными, остальные - светлыми.

Рис. 13. Эллипсометрическое изображение транзисторной структуры (с настройкой на подложку и на пленку)

Эллипсометрические методы контроля широко используются на следующих этапах разработки, исследования и контроля технологических процессов полупроводникового производства: контроль подготовки поверхности пластин, фотолитографических и электрохимических процессов, изучении электрофизических свойств полупроводниковых материалов; исследование нарушенных и ионноимплантированных слоёв полупроводников и диэлектриков; измерение толщины и показателей преломления диэлектрических плёнок и параметров эпитаксиальных структур; анализ явлений, возникающих на поверхности пластин при диффузии и термообработке.

ЛИТЕРАТУРА

1. Давыдов П. С. Техническая диагностика радиоэлектронных устройств и систем. - М.:Радио и связь, 2000. - 256 с.

2. Ермолов И.Н., Останин Ю.Я. Методы и средства неразрушающего контроля качества: Учеб. пособие для инженерно-техн. спец. вузов.-М.: Высшая школа, 2002. - 368 с.

3. Технические средства диагностирования: Справочник / Под общ. ред. В.В.Клюева. - М.: Машиностроение, 2005. - 672 с.

4. Приборы для неразрушающего контроля материалов и изделий. - Справоч­ник. В 2-х кн./ Под ред. В.В.Клюева - М.: Машиностроение, 2006.

5. Ж.Госсорг. Инфракрасная термография. Основы, техника, применение: Пер. с франц. – М. Мир, 2005. – 416 с.