| 1.01. В группе из 25 человек 10 учится на «отлично», 8 на «хорошо» и 7 на «удовлетворительно». Найти вероятность того, что из взятых наугад 8 человек 3 человека учатся на «отлично».
Решение. В данном случае испытание состоит в том, что из 25 человек наугад берутся 8 человек. При этом число всех равновозможных, несовместных и единственно возможных исходов равно
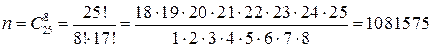 . .
Здесь мы используем сочетания, т.к. подмножества из 8 элементов неупорядочены.
Количество способов, которыми из 10 отличников можно взять 3, есть
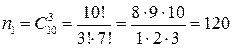
Остальных человек (не отличников) в группе из 8 человек у нас будет 8-3=5. Их мы выбираем из оставшихся 25-8=17 человек следующим числом способов: 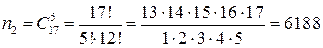
Далее, вероятность того, что в группе из 8 человек будут 3 отличника, вычисляем по классической формуле
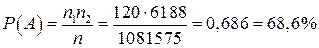
2.01. Программа экзамена состоит из 30 вопросов. Из 20 студентов группы 8 человек выучили все вопросы, 6 человек по 25 вопросов, 5 человек по 20 вопросов, а один человек 10 вопросов. Определить вероятность того, что случайно вызванный студент ответит на два вопроса билета.
Решение. Число способов составления билетов по два вопроса из 30 есть
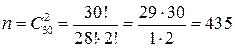
Для каждого из 8 человек, знающих все вопросы, число билетов будет тем же самым, т.е., вероятность найти билет с известными вопросами есть 1 или 100%. Доля таких студентов в группе есть 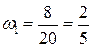 . .
Для следующих 6 человек возможное число билетов с известными вопросами есть 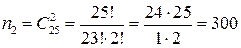 . Вероятность для них найти билет с известными вопросами есть . Вероятность для них найти билет с известными вопросами есть 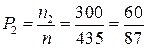 . Доля таких студентов в группе есть . Доля таких студентов в группе есть 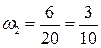 . .
Аналогично, для следующих 5 человек 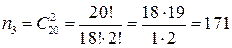 , , 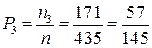 , их доля есть , их доля есть 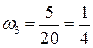 . .
Для того, кто знает только 10 вопросов, число выигрышных билетов есть 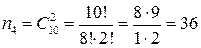 , , 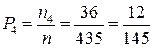 , его доля есть , его доля есть 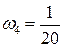 . .
Теперь воспользуемся формулой полной вероятности
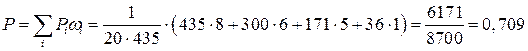 =70,9% =70,9%
3.01. Всхожесть семян некоторого растения составляет 80%. Найти вероятность того, что из 6 посеянных семян взойдёт: три, не менее трёх, не более четырёх.
Решение. Так как возможность одновременного всхода и гибели семени нереальна, это несовместные события, то вероятность гибели семени есть q=1-p=0,2.
Вероятность появления ровно 3 раза в серии из 6 событий находим по формуле Бернулли, так как число испытаний n
= 6 невелико (n
£ 10):
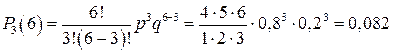
Не менее трёх ― это означает либо 3, либо 4, либо 5, либо 6. Вычислим вероятность проращивания всех 6 семян: Р6
(6)=0,86
=0,262.
Соответственно, 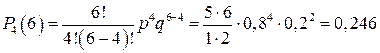
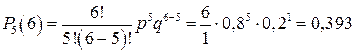
Следовательно, вероятность того, что взойдёт не менее 3 семян, есть
Рn≥3
(6)= P3
(6)+P4
(6)+P5
(6)+P6
(6)=0,082+0,262+0,246+0,393=0,983
Не более четырёх ― это значит, любое число, кроме 5 и 6, т.е., вероятность такого события есть
Рn≤4
(6)=1-(P6
(6)+P5
(6))=1-0,393-0,262=0,345
Ответ: 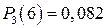 , Рn≥3
(6)=0,983, Рn≤4
(6)=0,345. , Рn≥3
(6)=0,983, Рn≤4
(6)=0,345.
4.01. Вероятность производства бракованной детали равна 0,008. Найти вероятность того, что из взятых на проверку 1000 деталей будет 10 бракованных.
Решение. В этой задаче число испытаний N
= 1000 достаточно велико (N
> 10), поэтому используем приближенные формулы Лапласа.
Число бракованных деталей равно 10, то есть 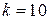 . Соответствующую вероятность находим по локальной формуле Лапласа. . Соответствующую вероятность находим по локальной формуле Лапласа.
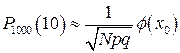 , где , где
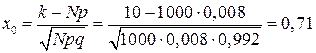 . .
Результат вычислений для x0
округляем с точностью до 0,01, так как значения функции φ(х0
) табулируются в с такой точностью. По специальной таблице, находим: φ(0,71)=0,3101.
Следовательно, 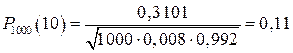
5.01. Из 25 контрольных работ, среди которых 5 оценены на «отлично», наугад извлекаются 3 работы. Найти закон распределения дискретной случайной величины Х ― числа работ, оцененных на отлично. Найти числовые характеристики случайной величины Х. Построить функцию распределения.
Решение. Имеем случайную величину Х ― число отличных работ. Её возможные значения 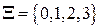 . .
Пусть у нас не попалось ни одной из отличных работ, т.е., вытянули все 3 не отличные. Вероятность этого есть 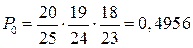
Пусть теперь есть только одна отличная работа. Она может быть вытащена в первый, во второй или только в третий раз. Вероятность такого события есть
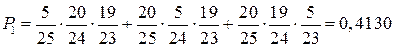 . Здесь 20 и 5 ― соответственно число не отличных и отличных работ в исходном массиве, 25, 24 и 23 ― число работ, последовательно уменьшающихся по мере того как мы выбираем их по одной. . Здесь 20 и 5 ― соответственно число не отличных и отличных работ в исходном массиве, 25, 24 и 23 ― число работ, последовательно уменьшающихся по мере того как мы выбираем их по одной.
Далее, пусть есть 2 отличных работы и соответственно 1 не отличная. Эта одна не отличная работа может попасться в первый, второй или третий раз:
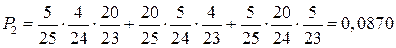
И наконец, единственный исход со всеми отличными работами:
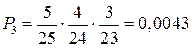
Полученные значения заносим в таблицу, которая и будет представлять закон распределения данной случайной величины:
| xi
|
0
|
1
|
2
|
3
|
| pi
|
0,4956
|
0,4130
|
0,0870
|
0,0043
|
Сумма всех вероятностей 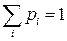
Для нахождения интегральной функции распределения воспользуемся её определением применительно к каждому промежутку изменения случайной величины
| x≤0
|
F(x)=P(x<0)=0
|
| 0≤x≤1
|
F(x)=P(x<1)=p0
=0,4956
|
| 1≤x≤2
|
F(x)=P(x<2)=p0
+p1
=0,4956+0,4130=0,9086
|
| 2≤x≤3
|
F(x)=P(x<3)=p0
+p1
+p2
=0,9956
|
| 3≤x≤∞
|
F(x)=1
|
Итак, искомая функция распределения выглядит следующим образом:
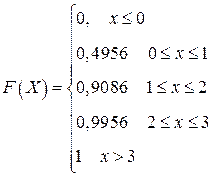
Чертим график

Найдём числовые характеристики случайной величины:
Мода М0
=1
Математическое ожидание
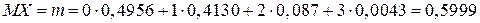
Дисперсия

Среднеквадратичное отклонение 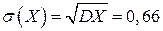
6.01. Случайная величина Х задана плотностью вероятностей
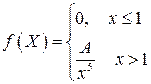
Определить параметр А, функцию распределения
F(
x), моду, математическое ожидание, дисперсию, среднеквадратичное отклонение, вероятность того, что в четырёх независимых испытаниях случайная величина Х попадёт 3 раза в интервал (0, 2). Построить графики функций
f(
x),
F(
x).
Решение. Так как ненулевая наша функция распределения только на интервале от 1 до ∞, то воспользуемся свойством нормировки плотности вероятности:
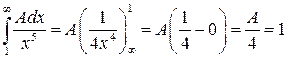 , откуда А=4 , откуда А=4
Таким образом, 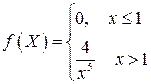
Чертим график такой функции

Найдём моду такой функции. Мо=1, так как наибольшее значение плотность вероятности принимает именно при x=1
Найдём медиану:
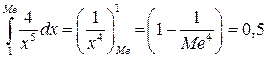 . Отсюда . Отсюда 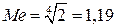
Найдём математическое ожидание
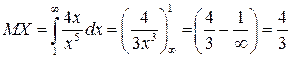
Дисперсия
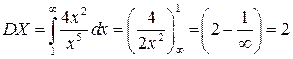
Среднеквадратичное отклонение 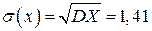
Найдём интегральную функцию распределения:
При x≤1, F(x)=0
При x>1 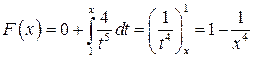
Таким образом, 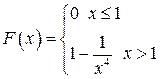
Вычерчиваем такой график

Вероятность того, что случайная величина попадает в интервал (0, 2) или фактически в интервал (1, 2), т.к. невозможны значения меньше 1, вычислим, проинтегрировав плотность вероятности в соответствующих пределах:
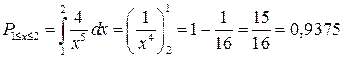 , так как на промежутке от 0 до 1 вероятность выпадения величины равна нулю. , так как на промежутке от 0 до 1 вероятность выпадения величины равна нулю.
Вероятность того, что только три из четырёх попаданий будет в этот интервал, вычислим по формуле Бернулли
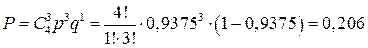
7.01. Срок службы прибора представляет собой случайную величину, подчинённую закону нормального распределения со средним сроком службы в 10 лет и среднеквадратичным отклонением 1,5 года. Определить вероятность того, что прибор прослужит до 15 лет, от 8 до 18 лет, свыше 16 лет.
Решение. Вероятность того, что величина Х попадает в некоторый интервал (α, β) есть 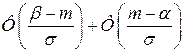 , где Ф ― функция Лапласа, m ― математическое ожидание распределения, σ ― среднеквадратичное отклонение. , где Ф ― функция Лапласа, m ― математическое ожидание распределения, σ ― среднеквадратичное отклонение.
В первом случае имеется от 0 до 15 лет, т.е., α=0, β=15
Следовательно, 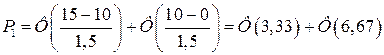 . Аргумент соответствующей функции Лапласа округляем до сотых. Обращаясь к таблице, выписываем: Ф(3,33)=0,4996 и Ф(6,67)=0,5000 . Аргумент соответствующей функции Лапласа округляем до сотых. Обращаясь к таблице, выписываем: Ф(3,33)=0,4996 и Ф(6,67)=0,5000
Следовательно, вероятность того, что прибор прослужит до 15 лет есть Р1
=0,4996+0,5=0,996
Соответственно, вероятность того, что он прослужит от 8 до 18 лет есть
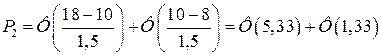 . Обращаясь к таблице, выписываем: Ф(1,33)=0,4082 и Ф(5,33)=0,5000. Следовательно, вероятность того, что он прослужит от 8 до 18 лет есть Р2
=0,5+0,4082=0,9082 . Обращаясь к таблице, выписываем: Ф(1,33)=0,4082 и Ф(5,33)=0,5000. Следовательно, вероятность того, что он прослужит от 8 до 18 лет есть Р2
=0,5+0,4082=0,9082
Свыше 16 лет ― это означает от 16 до бесконечности. 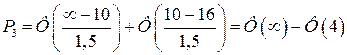 . Обращаясь к таблице, выписываем: Ф(∞)=0,5 и Ф(4)=0,499968. Следовательно, такая вероятность Р3
=0,5-0,499968=3,2·10‑5
. . Обращаясь к таблице, выписываем: Ф(∞)=0,5 и Ф(4)=0,499968. Следовательно, такая вероятность Р3
=0,5-0,499968=3,2·10‑5
.
8.01. Имеются данные о продаже туристических товаров в системе спорткультторга по кварталам за 5 лет в тыс. у.е. рассчитать гарантийный запас товара в тыс. у.е. на квартал с указанной надёжностью γ и проанализировать плановые товарные запасы на квартал

Решение. Поскольку σ неизвестно, то гарантийный запас обуви найдём по формуле 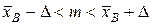 , где , где 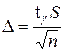 . По таблице Стьюдента с уровнем значимости α=1-0,96=0,04 и числом степеней свободы k=n-1=19 найдем tγ
=2,20. . По таблице Стьюдента с уровнем значимости α=1-0,96=0,04 и числом степеней свободы k=n-1=19 найдем tγ
=2,20.
Составляем расчётную таблицу для нахождения 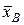 и S. и S.
| №
|
xi
|
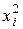
|
№
|
xi
|
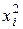
|
| 1
|
396
|
156816
|
12
|
418
|
174724
|
| 2
|
438
|
191844
|
13
|
412
|
169744
|
| 3
|
398
|
158404
|
14
|
480
|
230400
|
| 4
|
412
|
169744
|
15
|
478
|
228484
|
| 5
|
414
|
171396
|
16
|
519
|
269361
|
| 6
|
422
|
178084
|
17
|
429
|
184041
|
| 7
|
436
|
190096
|
18
|
437
|
190969
|
| 8
|
418
|
174724
|
19
|
391
|
152881
|
| 9
|
443
|
196249
|
20
|
368
|
135424
|
| 10
|
474
|
224676
|
Σ
|
8633
|
3750561
|
| 11
|
450
|
202500
|
|
|
|
Параметры вычисляем по формулам:
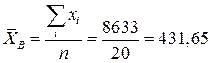
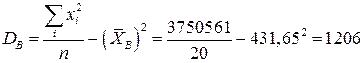
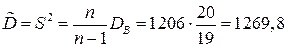
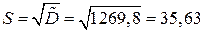
Тогда 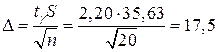
Границы доверительного интервала ― это 431,65-17,5=414,12 слева и 431,65+17,5=449,18
Таким образом, гарантийный квартальный запас должен быть не менее 414,12 тыс. у.е. и не более 449,18 тыс. у.е. В эти рамки должно укладываться не менее 96% произведённых выборок.
План 460 тыс. у.е. не соответствует этому интервалу.

Определить тесноту связи между
X и
Y, составить уравнение регрессии.
Решение. Для определения характера зависимости построим точки xi
, yi
.
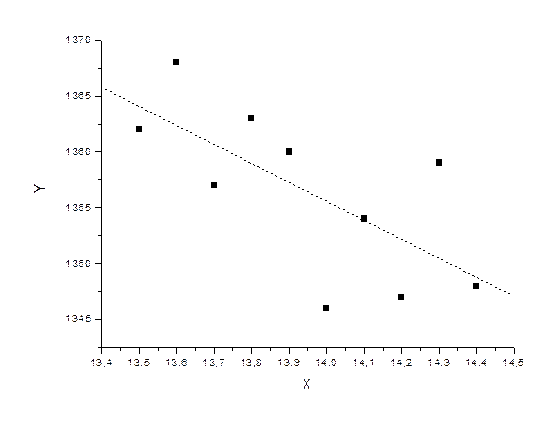
Видно, что все точки, кроме (14, 1346), (14,3, 1359) группируются около некоторой прямой. Следовательно, можно говорить о линейной регрессии.
Будем искать уравнение регрессии в виде 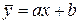
| №
|
xi
|
yi
|
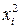
|
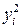
|
xi
yi
|
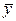
|
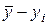
|
| 1
|
13.5
|
1362.0
|
182.25
|
1855044
|
18387
|
1364.04
|
2.04
|
| 2
|
13.6
|
1368.0
|
184.96
|
1871424
|
18604
|
1362.34
|
5.66
|
| 3
|
13.7
|
1357.0
|
187.69
|
1841449
|
18590
|
1360.64
|
3.64
|
| 4
|
13.8
|
1363.0
|
190.44
|
1857769
|
18809
|
1358.95
|
4.05
|
| 5
|
13.9
|
1360.0
|
193.21
|
1849600
|
18904
|
1357.25
|
2.75
|
| 6
|
14.0
|
1346.0
|
196.00
|
1811716
|
18844
|
1355.55
|
9.55
|
| 7
|
14.1
|
1354.0
|
198.81
|
1833316
|
19091
|
1353.85
|
0.15
|
| 8
|
14.2
|
1347.0
|
201.64
|
1814409
|
19127
|
1352.16
|
5.16
|
| 9
|
14.3
|
1359.0
|
204.49
|
1846881
|
19433
|
1350.46
|
8.54
|
| 10
|
14.4
|
1348.0
|
207.36
|
1817104
|
19411
|
1348.76
|
0.76
|
| Σ
|
139,5
|
330
|
1946,85
|
18398712
|
189203
|
-
|
-
|
Искомые параметры a
и b
найдём из системы уравнений
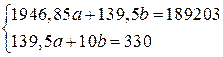
а
=-16,96969 и b=1593,12727. Следовательно, искомая аппроксимирующая функция есть y=-16,96969х+1593,12727
Рассчитаем по этому уравнению ожидаемые значения выпечки хлеба. По значениям отклонений можно сделать вывод о том, что ожидаемые значения 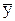 удовлетворительно согласуются с наблюдаемыми значениями у. удовлетворительно согласуются с наблюдаемыми значениями у.
Найдём выборочный коэффициент корреляции
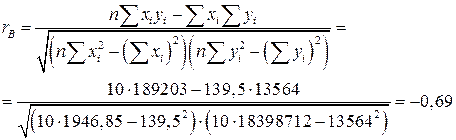
Коэффициент корреляции по модулю равен 0,69 ― связь заметная, обратная (по шкале Чаддока).
|