|
федеральное агентство по образованию
ростовский институт (филиал)
государственного образовательного учреждения высшего профессионального образования
"российский государственный торгово-экономический университет"
Кафедра высшей и прикладной математики
Контрольная работа № 1
по дисциплине «Высшая математика»
Вариант № 0
Выполнил: Афонин В.П.
студент 2-го курса, группы УТ,
заочной формы обучения.
Преподаватель:______________
Ростов-на-Дону
2006 г
.
План работы.... 2
Задача 1. 2
Задача 2. 2
Задача 3. 2
Задача 4. 2
Задача 5. 2
Задача 6. 2
Задача 7. 2
Задача 8. 2
Задача 9. 2
Задача10. 2
Использованная литература.. 2
Вычислить пределы функций а) - е):
а)
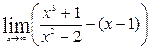 ; б) ; б)
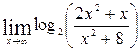 ; ;
в)
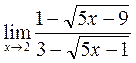 ; г) ; г)
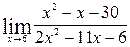 ; ;
д)
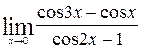 ; е) ; е)
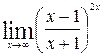 ; ;
Решение
а)
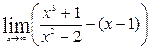 =
Мы имеем дело с неопределенностью вида =
Мы имеем дело с неопределенностью вида 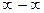 . Приводим выражение к общему знаменателю: . Приводим выражение к общему знаменателю:
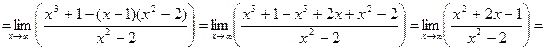
Тогда вынесем х в старшей степени за скобку в числителе и знаменателе 1-й дроби и знаменателе второй дроби после чего - сократим. Получим:
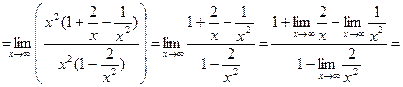
Устремим х к ∞, получим|
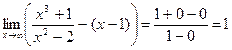
Ответ:
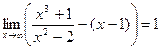
б)
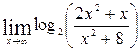 Так как функция Так как функция 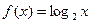 непрерывна на (0;∞) , то
непрерывна на (0;∞) , то 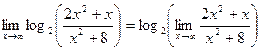 Мы имеем дело с неопределенностью вида
Мы имеем дело с неопределенностью вида 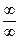 . Тогда вынесем х2
скобку в числителе и знаменателе и сократим. Получим: . Тогда вынесем х2
скобку в числителе и знаменателе и сократим. Получим:
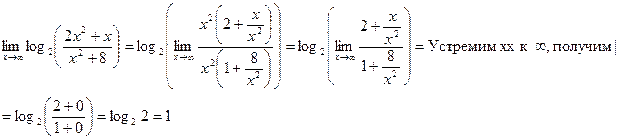
Ответ:
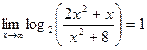
в)
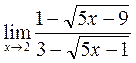 ; В данном случаем м
ы имеем дело с неопределенностью вида ; В данном случаем м
ы имеем дело с неопределенностью вида 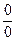 . Выражение . Выражение 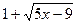 является сопряженным по отношению к выражению
является сопряженным по отношению к выражению 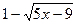 , а
, а 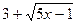 к выражению
к выражению 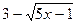 соответственно. Умножая числитель и знаменатель дроби на произведение сопряженных выражений
соответственно. Умножая числитель и знаменатель дроби на произведение сопряженных выражений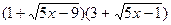 , и используя формулу
, и используя формулу 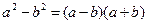 , получим:
, получим:
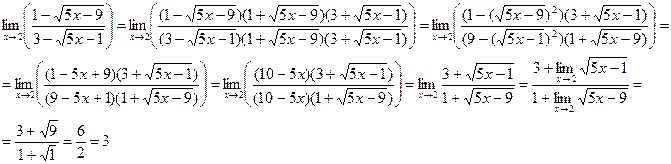 Ответ: Ответ:
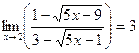
г) 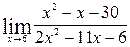
Подстановка числа 6 вместо х показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределённость 0/0. Для этого можно либо провести тождественные преобразования выражения 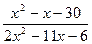 , либо применить правило Лопиталя.
, либо применить правило Лопиталя.
Уравнение 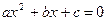 тождественно уравнению
тождественно уравнению 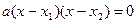 где x1
и x2
корни квадратного уравнения
где x1
и x2
корни квадратного уравнения 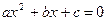 Исходя из этого получаем: =
Исходя из этого получаем: =
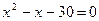
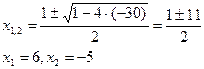 ,аналогично ,аналогично
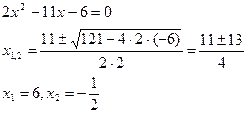
Таким образом:
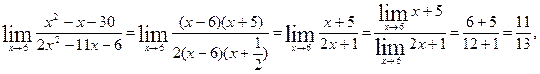
Другое решение задачи. Воспользуемся правилом Лопиталя
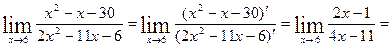
так как функция непрерывна в точке х=6, подставляем х=6
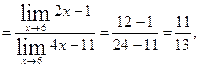
Ответ:
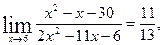
д) 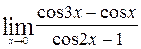
Подстановка числа 0 вместо х показывает, что предел числителя и предел знаменателя при х→0 равны нулю. Поэтому имеет место неопределённость 0/0. Для того, чтобы раскрыть неопределённость можно либо провести тождественные преобразования выражения 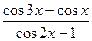 , либо применить правило Лопиталя.
, либо применить правило Лопиталя.
1. Совершим необходимые тождественные, тригонометрические преобразования:
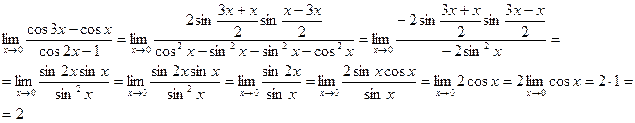
2. Другое решение задачи. Воспользуемся вновь правилом Лопиталя
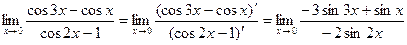
Снова имеем неопределенность 0/0. Применяем правило Лопиталя:
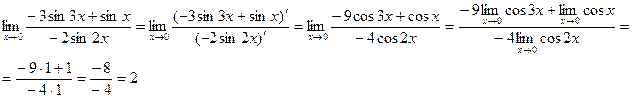
Ответ:
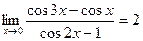
е) 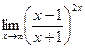
Решение. 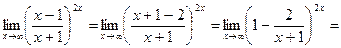
замена переменной 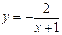 ; так как ; так как 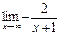 =0, то y→0, следовательно: =0, то y→0, следовательно:
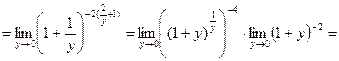
используем второй замечательный предел 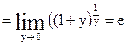
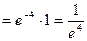
Ответ:
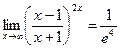
Вычислить производные функции а)-г).
а)
 ; б) ; б)
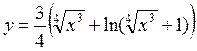
в)
у = (sinx) • e2
x
• ln(sinx); г)
у =(sinx)lnx
.
Решение
а)
 ,Используем формулу производной дроби: ,Используем формулу производной дроби: 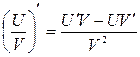
и формулу производной степенной функции: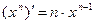 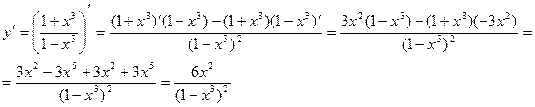
Ответ:
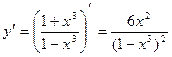
.б)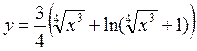 ,Найдём сначала производную функции ,Найдём сначала производную функции 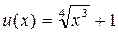 , используя формулу производной степенной функции: , используя формулу производной степенной функции: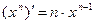
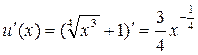
Теперь находим в таблице производных сложных функций формулу 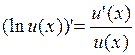 подставляя подставляя 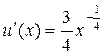 , получаем , получаем
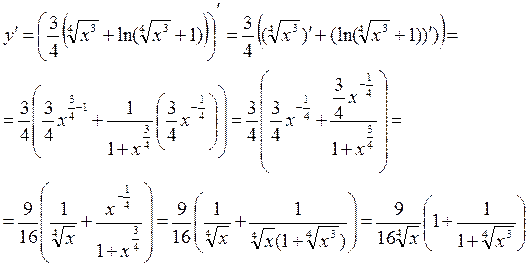
Ответ:
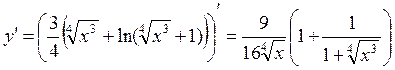
в)
у = (sinx) • e2
x
• ln(sinx);
Функция у(х) представляет собой произведение трёх функций u(х)= (sinx), v(x)= e2
x
и w(x)= ln(sinx). Используя правило Лейбница, можно вывести общую формулу:
(u·v·w) '=u'·(vw)+u· (vw)'=u'vw+u· (v'·w+v·w')
Следовательно,
(uvw)'=u'· v·w+u·v'·w+u·v·w'
Далее используя формулу производной сложной функции 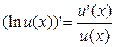
Получаем:
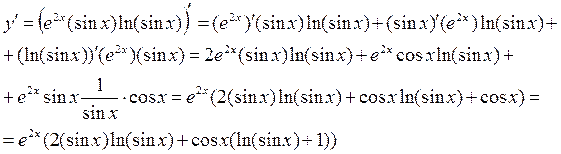
Ответ:
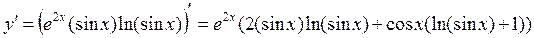
г) у =(sinx)lnx
Пользуясь основным логарифмическим тождеством y=elny
, представим y(x) в виде y(x)=(eln
(
sinx
)
)lnx
. Так как (ab
)c
=abc
, то y(x)= e lnx
ln
(
sinx
)
. и поэтому
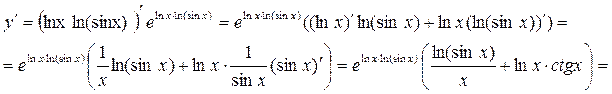
В последнем равенстве мы вновь воспользовались формулой у =(sinx)lnx
= e lnx
ln
(
sinx
)
.
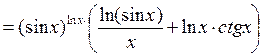
Ответ:
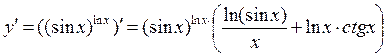
а). Исследовать функцию у(х)=2
x
3
- 9
x
2
+ 12
x
- 5.
Решение
1). Так как 2
x
3
- 9
x
2
+ 12
x
- 5
— многочлен, то функция у(х) определена и непрерывна на всей числовой прямой. Таким образом, область определения данной функции вся — числовая прямая: D(y)=(–∞;+∞).
2). Функция не является ни чётной ни нечётной, поскольку
y(1)=0; y(–1)=–28; у(–1)≠у(1); y(1)≠y(-1).
3). Заметим, что при х→+∞ и при х→–∞ поведение многочлена у(х) определяется поведением его старшего члена 2х3
, который неограниченно возрастает при х→+∞ и неограниченно убывает при х→–∞. Поэтому
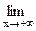 y(x)= +∞, l y(x)= +∞, l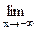 y(x)=–∞, y(x)=–∞,
Так как функция у(х) определена на всей числовой оси и 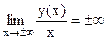 , график функции не имеет асимптот. , график функции не имеет асимптот.
4). у(0) = -5 → A(0; -5) — точка пересечения графика с осью Оу.
Для определения точек пересечения графика с осью Оx решим уравнение
у(х)=0 ↔ 2x3
- 9x2
+ 12x - 5=0 ↔ x•(2х2
+ 15x + 24) = 0;
Методом подбора определяем корень уравнения х1
=1.
Разделим многочлен на многочлен x
-1
 2x3
- 9x2
+ 12x – 5 x
-1 2x3
- 9x2
+ 12x – 5 x
-1
    2x3
- 2x2
2x2
- 7x + 5 2x3
- 2x2
2x2
- 7x + 5
- 7x2
+12х
- 7x2
+7х
5x – 5
5x – 5
0
2x2
- 7x + 5= 0,
D=b2
–4ac=-72
–4•2•5=49- 40=9
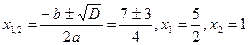
Точки пересечения с осью Ох: B(1;0), С(5/2;0),
5). Находим локальные экстремумы, а также промежутки возрастания и убывания функции. Для этого вычисляем производную функции у(х):
у'(х)=(2x3
- 9x2
+ 12x - 5)´,
у'(х)=6x2
- 18x + 12 ,
у'(х)=x2
- 3x + 2 ,
и решаем уравнение у'(х)=0:
x2
- 3x + 2 = 0, критические точки х1
= 1, x2
= 2.
Так как производная не имеет точек разрыва, других критических точек нет. Определяем знак производной справа и слева от каждой критической точки и составляем таблицу:
| x
|
(–∞;1)
|
1
|
(1;2)
|
2
|
(2; +∞)
|
| y'
|
+
|
0
|
–
|
0
|
+
|
| y
|

|
Максимум
|
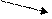
|
Минимум
|

|
Итак, функция возрастает при х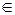 [–∞; 1] и при х [–∞; 1] и при х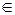 [2; +∞] и убывает при х [2; +∞] и убывает при х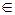 [1; 2]; локальный минимум — у(2)=–1, локальный максимум — у(1)=0. [1; 2]; локальный минимум — у(2)=–1, локальный максимум — у(1)=0.
6). Используя пункт 3), получаем, что множество значений функции Е(y) — вся числовая прямая, Е(у) = (—∞; +∞).
7). Находим точки перегиба функции и устанавливаем промежутки, на которых график функции обращен выпуклостью вверх и вниз. Для этого, прежде всего, вычисляем производную второго порядка и приравниваем её к нулю:
у''(х)= (у'(х))'=(x2
- 3x + 2)'=2х-3
у"(х)=0 ↔ 2х - 3= 0 ↔ х=3/2=1,5.
Для определения знаков второй производной подставляем в неё числа из промежутков 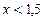 и : и : 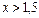 у"(0)=–3; у"(2)=1. у"(0)=–3; у"(2)=1.
| x
|
(–∞;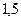 ) )
|
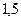
|
(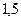 ; +∞;) ; +∞;)
|
| y''
|
–
|
0
|
–
|
| y
|
Выпуклость вверх
|
Перегиб
|
Выпуклость вниз
|
Теперь необходимо найти значение функции в точке перегиба и определить угол наклона касательной к графику функции в этой точке:
у(1,5)=-0,5, тангенс угла наклона равен значению производной в данной точке у'(1,5)=tgα=1,5. Следовательно, касательная к графику проходит через точки D(1,5; -0,5) Е(3,5;-3,5). Проводим через точки в и E прямую (DE). График функции у(х) должен касаться прямой (DE) в точке D.
8). На этом исследование функции закончено и остаётся лишь вычислить её значения в некотором числе точек, достаточном для построения графика, и построить график.
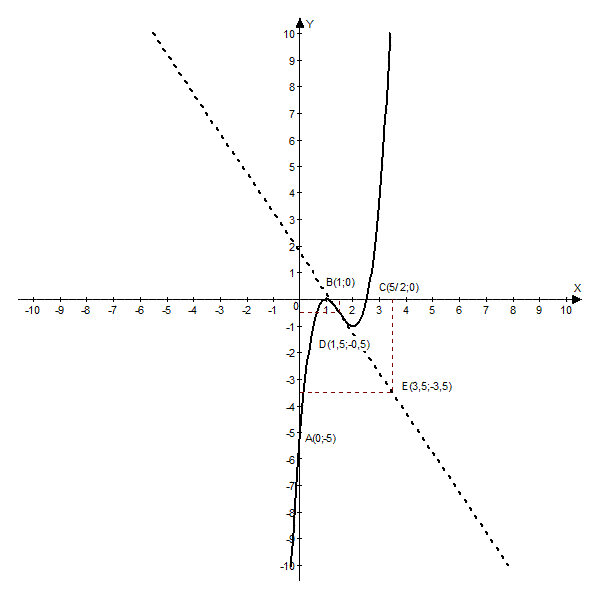
б
). Исследовать функцию 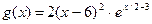 . .
Решение
1). Так как в 2(х - 6)2
= R и D(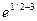 )=М, то функция g(х) определена и непрерывна на
)=М, то функция g(х) определена и непрерывна на
всей числовой прямой.
2). Функция не является ни чётной ни нечётной, поскольку
g(1)= 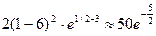 ;
;
g(-1) = 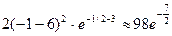 и g(–1)≠g(1)
и g(–1)≠g(1)
3) 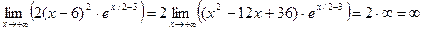
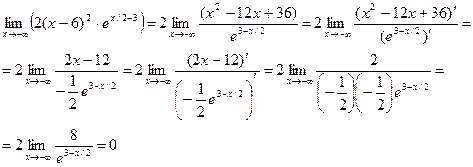
Следовательно, nак как функция g(х) определена на всей числовой оси и 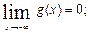 функция имеет левую горизонтальную асимптоту y =0. функция имеет левую горизонтальную асимптоту y =0.
4). Так как g(0)=2(0-6)2
•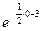 =72 =72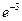 ≈3,58, то А(0;72 ≈3,58, то А(0;72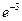 ) — точка пересечения графика с осью Оу. ) — точка пересечения графика с осью Оу.
Для определения точек пересечения графика с осью Ох решим уравнение g(х)=0, т. е. 2•(x-6)2
•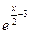 =0. Так как любая степень числа е положительна, мы можем разделить на 2 =0. Так как любая степень числа е положительна, мы можем разделить на 2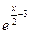 обе части уравнения: обе части уравнения:
(x-6)2
= 0; D=144-144=0; x=6.
График функции пересекает ось Ох в точке B(6;0) и в силу своей непрерывности, функция g(х) не меняет своего знака на протяжений всей числовой оси т.к. 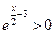 и 2•(x-6)2
>0. Отсюда вытекает, что g(х)>0 для всех действительных чисел x. и 2•(x-6)2
>0. Отсюда вытекает, что g(х)>0 для всех действительных чисел x.
5). Экстремумы. Промежутки возрастания и убывания.
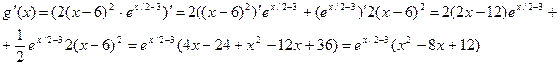
Для определения критических точек функции решим уравнение
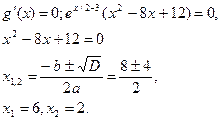
g(х)=0 ↔ –(х2
+ 5х + 4) • е-1/2(
x
+3)
=0 ↔ х2
+ 5х + 4 = 0;
критичαеские точки — х1
= 6, x2
= 2.
| x
|
(–∞;2)
|
2
|
(2;6)
|
6
|
(6; +∞)
|
| g'
|
+
|
0
|
–
|
0
|
+
|
| g
|

|
32/e2
Максимум
|

|
0
Минимум
|

|
Локальный максимум— g(2)= 2•(2-6)2
•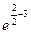 ≈32/e2
, локальный минимум — ≈32/e2
, локальный минимум —
g(6)= 2•(6-6)2
•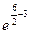 =0• =0•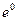 =0. =0.
6). Используя пункты 3) - 5), получаем, что Е(у)=(0;+∞). ´ββ
7). Находим точки перегиба и промежутки выпуклости.
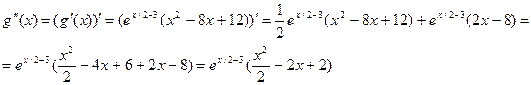
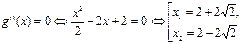
| x
|
(–∞;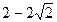 ) )
|
(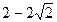 ) )
|
(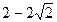 ; ;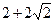 ) )
|
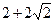
|
(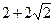 ; +∞) ; +∞)
|
| g'
|
+
|
0
|
–
|
0
|
+
|
| g
|
Выпуклость вниз
|
Перегиб
|
Выпуклость вверх
|
Перегиб
|
Выпуклость вниз
|
Теперь необходимо найти значение функции и значение производной (тангенс угла наклона касательной к графику функции) в точках перегиба:
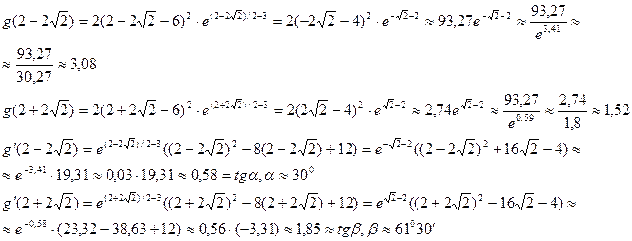 Вычислить значение функции в некотором числе промежуточных точек:
Вычислить значение функции в некотором числе промежуточных точек:
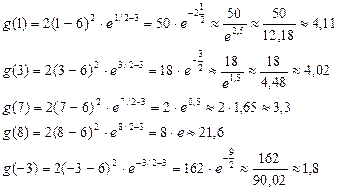
9). Строим график функции.
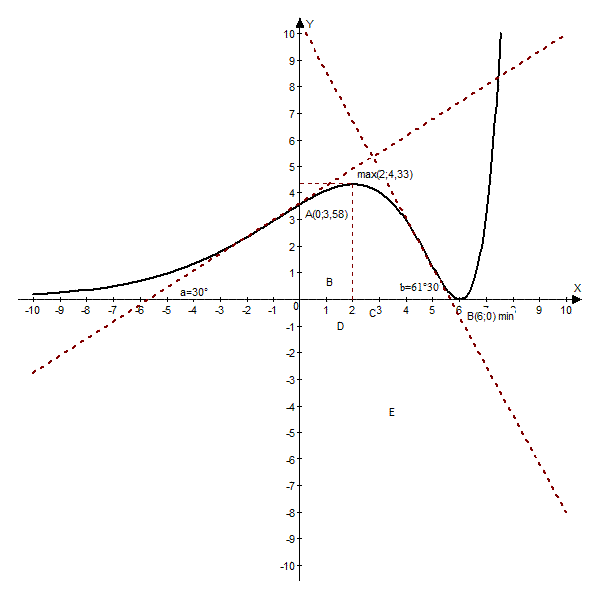
Вычислить неопределённые интегралы а) - г):
а)
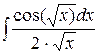 б)
б)

в)
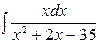 г)
г)
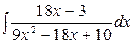
Решение
a) 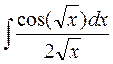
Сделаем подстановку 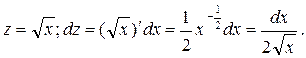 Тогда Тогда
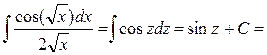 , памятуя что , памятуя что 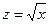 получаем получаем
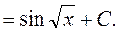
Ответ:
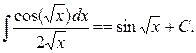
б) 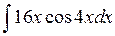
Решение данной задачи основано на формуле интегрирования по частям по формуле: 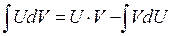 (1) (1)
В этой формуле принимаем за u функцию x и du=dx. Тогда 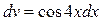 и и 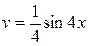 (так как мы находим первообразную, то «+С» не пишем). Подставим найденные u',v', u,
v' в формулу интегрирования по частям b используя (так как мы находим первообразную, то «+С» не пишем). Подставим найденные u',v', u,
v' в формулу интегрирования по частям b используя 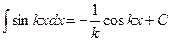 получаем: получаем:
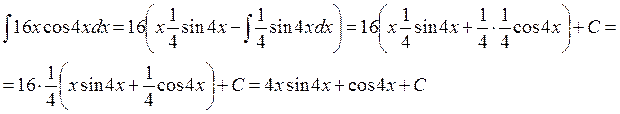
Ответ:
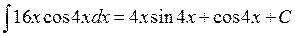
в) 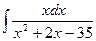
Найдем корни уравнения 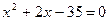 . Так как корнями уравнения является х1
=-7 и х2
=5, то по формуле ах2
+bх+с=а(х+7)(x—5), знаменатель раскладываются на множители . Так как корнями уравнения является х1
=-7 и х2
=5, то по формуле ах2
+bх+с=а(х+7)(x—5), знаменатель раскладываются на множители
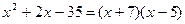 . .
Представим дробь в виде следующей суммы:
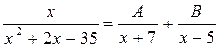
и найдём коэффициенты А и В. Приведём дроби в правой равенства части к общему знаменателю:
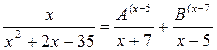
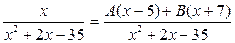
Приравняв числители, получим
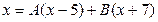
Подставляя в последнее равенство х = 5, находим, что
5 = А(5 – 5) +B(5+7) ↔ 5 = B • (12) ↔ B= 5/12.
Подставляя х=-7 в равенство (2), находим, что
-7 = A(-7–5) +B(-7+7) ↔ -7=A • (-12) ↔ А = 7/12.
Таким образом, 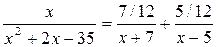
Итак, 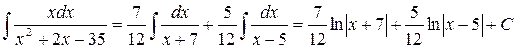
Ответ:
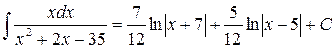
г) 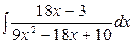 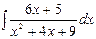
Напомним, что в том случае, когда дискриминант квадратного ах2
+ bх + с двучлена отрицателен, D=b2
—4ас<0, справедливо равенство:
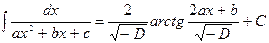
Для вычисления интеграла 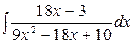 найдем дискриминант знаменателя D=182
—4•9•10=324-360=-36<0 и рассмотрим функцию у=9х2
-18x+10. Для последующей замены переменной вычислим производную знаменателя у'=(9х2
-18x+10)'=18x-18 и заметим, что 18х-3=(18x-18)+15. найдем дискриминант знаменателя D=182
—4•9•10=324-360=-36<0 и рассмотрим функцию у=9х2
-18x+10. Для последующей замены переменной вычислим производную знаменателя у'=(9х2
-18x+10)'=18x-18 и заметим, что 18х-3=(18x-18)+15.
Отсюда,
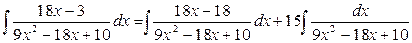
Вычислим получившиеся интегралы по отдельности.
1)
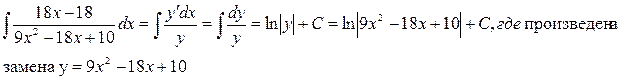
2) 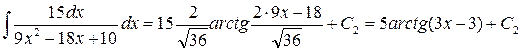
Подставляя полученные выражения, окончательно получаем следующий ответ:
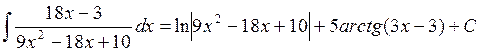
Ответ:
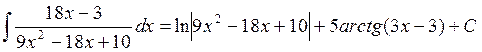
Вычислить площадь фигуры, ограниченной графиками функций
g
(х)=3х+4 и
f
(х) = -3х2
+21
x
-11. Изобразить эту фигуру на координатной плоскости.
Решение
Графиком функции f(х) является парабола, ветви которой направлены вверх. Вычисляем производную функции f'(х)= - 6х+21 и находим координаты вершины параболы С:
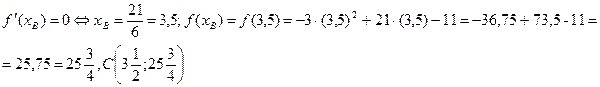 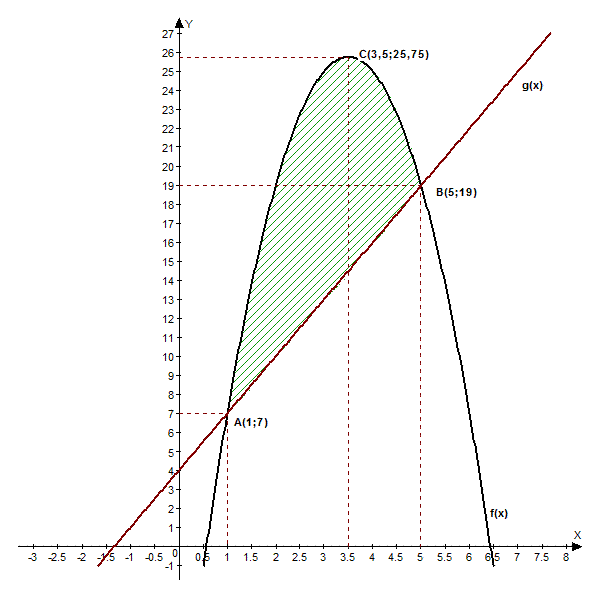
Графиком функции g(x)=3x+4 является прямая, проходящая через точки (0;4), (-4/3;0).
Найдём точки пресечения графиков функции: g(х)=f(x)
-3х2
+21x-11= 3x+4 ↔ -3х2
+ 18х -15 = 0 ↔ х2
- 6х + 5 = 0 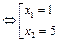
Заметим, что g(1) = f(1) = 7, g(5) = f(5) = 19.
Пусть S — площадь фигуры ABC, ограниченной графиками функций. Так как f(x)≥ g(х) при х 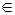 [1;5], то [1;5], то
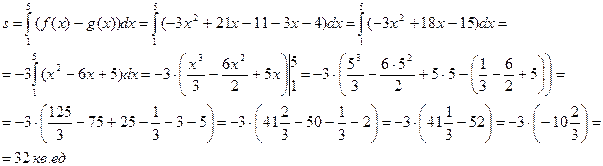
Ответ:
32 кв.ед
Найти общее решение дифференциального уравнения
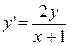 . Построить графики двух частных решений этого уравнения. . Построить графики двух частных решений этого уравнения.
Решение.
1). Преобразуем уравнение к виду 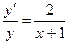 . .
2) 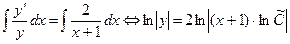 , где , где 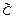 - const. - const.
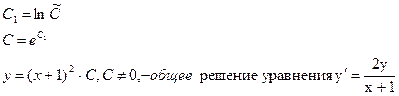
Графиком частных решений данного уравнения является множество парабол с общей вершиной в точке А(-1;0)
Положив С1
=1, и С2
=-1 построим графики двух частных решений
y1
=(x+1)2
,
y2
= -(x+1)2
,
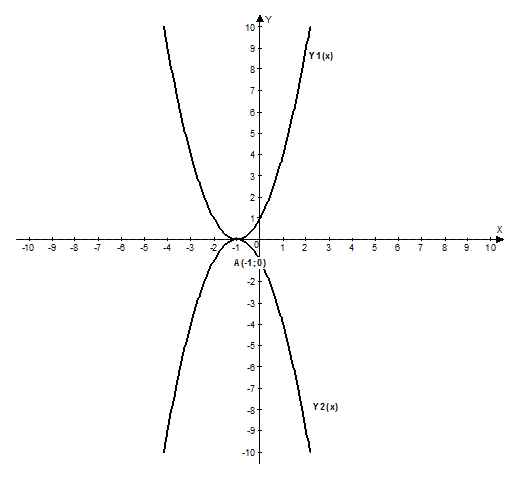
Ответ:
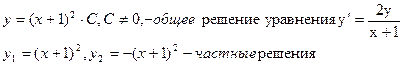
Найти частное уч
.(х) решение дифференциального уравнения у'
cosx
+
у
sinx
=2, удовлетворяющее (начальному) условию: уч
(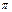 )=2. )=2.
Решение.
1). Разделим обе части уравнения на cosx:
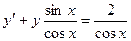
Подставляя вместо у произведение двух функций y=uv, y'=u'v+uv'
получаем уравнение:
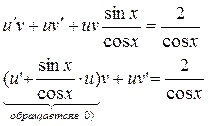 (1) (1)
2). Найдём теперь какую-нибудь функцию u для которой выполняется равенство
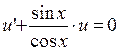
Для этого найдём частное решение дифференциального уравнения
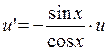
Если функции равны, то и неопределённые интегралы от них равны:
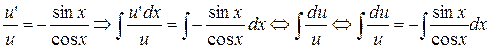
Так как нам нужно найти частное решение, полагаем С=0, т.е. приравниваем первообразные подынтегральных функций:
ln u= ln cos x ↔ u= cos x.
3). Подставляя у = cos x в уравнение (1), получим
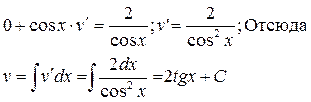
Так как всякая функция с точностью до константы равна неопределённому интегралу от собственной производной, то
у=u•v =cosx•(2•tgx + C) = cosx•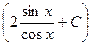 =2•sinx+C•cosx. =2•sinx+C•cosx.
Итак, общее решение дифференциального уравнения имеет вид
у=2•sinx+C•cosx.
4). Для отыскания частного решения необходимо и достаточно определить значение неопределённой постоянной С по начальному условию, данному в задаче. Используя то условие, что уч
=2 при 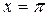 , получаем равенство: , получаем равенство:
2=2•sinπ+C•cosπ; памятуя, что sinπ=0 и cosπ=-1, получаем:
2=2•0-C;
Отсюда С=-2. Подставляя найденное значение неопределённой постоянной, получаем частное решение уч
.=2(sinx-cosx), удовлетворяющее условию, данному в задаче.
Ответ:
у=2•sinx+C•cosx – общее решение,
уч
.=2(sinx-cosx) – частное решение
Найти частное решение дифференциального уравнения
y
''–
у'–6
y
=2
sin
2
x
–10
cos
2
x
, удовлетворяющее начальным условиям у(0)=2, у'(0) = 3.
Решение.
1). Уравнение вида у" + bу' + су =0, где b и с — некоторые числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Общее решение уо
o
.(x) этого уравнения в зависимости от знака дискриминанта в = b2
— 4aс характеристического уравнения k2
+ bk + с =0
В нашем случае характеристическое уравнение: k2
—k — 6=0.
D=1+24=25>0
Так как D>0 используем формулу уо
.о
.=С1
еαх
+ С2
еβх
, , где k=α, k=β — два различных действительных корня (α≠β) характеристического уравнения. В нашем случае: α=3, β=-2. Общее решение однородного уравнения:
уoo
(х)= С1
е3х
+ С2
е-2х
2). Так как правая часть f(х)= 2sin2x–10cos2x и k2
+22
≠ k2
—k — 6 частное решение неоднородного уравнения будем искать в виде:
уч
(х) = Аcos2x + Вsin2x + С,
у'ч.
(x) = -2Аsin2х + 2Вcos2x,
у"ч.
(х) =-4Аcos2х -4Вsin2x,.
Подставляя у = уч
.(x) в данное в задаче уравнение, получаем:
-4Аcos2х - 4Вsin2x + 2Аsin2х - 2Вcos2x - 6Аcos2x - 6Вsin2x = 2sin2x–10cos2x
cos2х(-4А - 2В - 6А) +sin2x(- 4В + 2А- 6В) = 2sin2x–10cos2x,
cos2х(-10А - 2В) +sin2x(2А- 10В) = 2sin2x–10cos2x,
Сравнивая коэффициенты при cos2x и sin2x, находим:
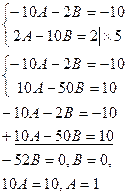

Отсюда уч.
(x)=cos2x, поэтому так, как уо
.н
.(х) = уoo
(х) + уч.
(x), общее решение неоднородного уравнения имеет вид уо
.н
.(х) = С1
е3х
+ С2
е-2х
+ cos2x.
3). Находим частное решение, удовлетворяющее начальным условиям, данным в задаче:
у(0) = 2 → C1
e0
+ С2
е0
+ cos 0 = 2 => С1
• 1 + С2
• 1 = 1, => С1
+ С2
= 1,
у'(x) = 3С1
е3х
-2С2
е-2х
– 2sin2x.
у'(0) = 3C1
е0
-2C2
е0
-2sin 0= 3 → 3C1
- 2C2
- 0= 3 => 3C1
- 2C2
=3.
Ответ: у (х) = ех
cos 2x + ½ еx
sin2x + х2
.
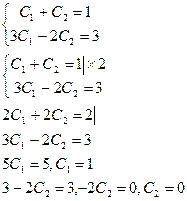
Следовательно, частное решение, удовлетворяющее начальным условиям, данным в задаче: у(х) = 1 • е3х
+ 0 • е-2х
+ cos2x= е3х
+ cos2x.
Ответ:
у(х) = е3х
+ cos2x.
Исследовать сходимость ряда
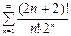
Решение.
Используем признак Даламбера
. Если существует предел 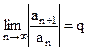 , то числовой ряд , то числовой ряд 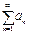 сходится при q < 1 и расходится при q > 1. сходится при q < 1 и расходится при q > 1.
В нашем случае 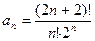 и и 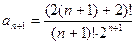 . Вычисляем предел: . Вычисляем предел:
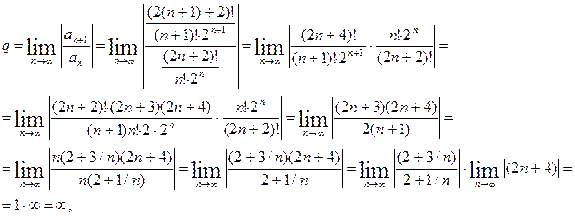
так как q = ∞ > 1, то ряд расходится.
Ответ:
Так как
q
>
1, то ряд расходится.
Найти радиус и интервал сходимости степенного ряда
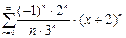
Решение.
Каждый степенной ряд 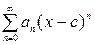 сходится внутри интервала (с —R; с + R), где R≥0 — радиус сходимости, определяемый по формуле сходится внутри интервала (с —R; с + R), где R≥0 — радиус сходимости, определяемый по формуле 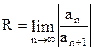 . .
Определяем радиус сходимости:
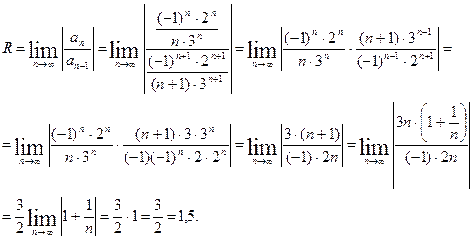
Так как с = -2; с–R=–2–1,5=–3,5; с+R==–2+1,5=–0,5, находим интервал сходимости: (–3,5; –0,5).
Исследуем на сходимость в точках x=-3,5 и x=-0,5. При x=-3,5 ряд имеет вид:
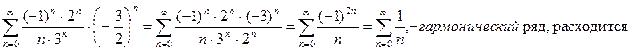
При x=-0,5 ряд имеет вид:
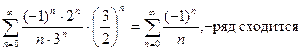 . .
Поэтому интервал сходится и будет (-3,5;-0,5], R=1,5
Ответ:
R = 1,5; (-3,5;-0,5].
1. Высшая и прикладная математика. Конспект лекций. Часть I. Высшая математика. Выпуск 1. Основы математического анализа. М.: МКУ, 1993.
2. Зайцев М.В., Лавриненко Т.А. Высшая математика. Сборник задач, часть 1. М.: изд. МГУК, 1998.
3. Карасев А. И., Аксютина 3. М., Савельева Т. И. Курс высшей математики для экономических вузов. Ч. 1. М.: Высшая школа, 1982.
4. Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. М.: Наука, 1989.
5. Маркович Э. С. Курс высшей математики с элементами теории вероятностей и математической статистики. М.: Высшая школа, 1972.
6. Минорский В. И. Сборник задач по высшей математике. М.: Наука, 1986.
7. Шипачев B.C. Задачник по высшей математике. М.: Высшая школа, 1998.
|